ランキング入りしている大学を地域で比べた時に特徴的な地域はあるのか
目的
大学ランキングに入っている大学を地域で比べた時に特徴的な地域がないか見ていきます。
データをチェックする
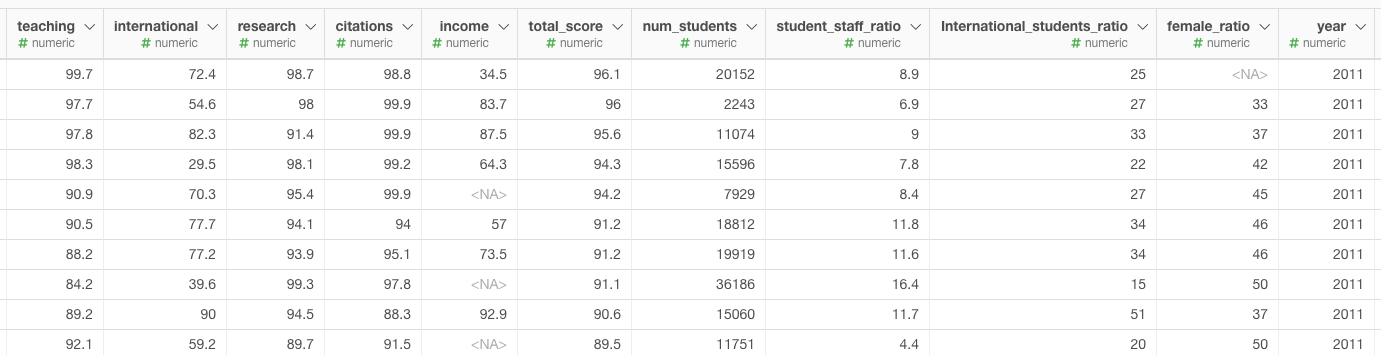
まずはRankingデータに文字が入っていたり、範囲を示すような表記があるので以下のように少し綺麗にしたいと思います。
次に年毎にランキング入りしている大学の数の分布を見ていきます。2011年から2012年にかけてと、2015年から2016年にかけて大学数が大きく増えていることが分かります。ただ今こが何を意味しているかは分かりませんが念の為メモとして残しておきます。
次にどの国がランキングに占める割合が大きいかを年ごとに見ていきたいと思います。
そうすると、アメリカやイギリスなどいくつかの特定の国の割合が高いことが確認できました。更に2016年にいくつかの新しい国が追加されていることも分かります。こちらも背景は分かりませんがメモとして残しておきます。
続いて、先程の集計結果をより大きな枠組みである大陸レベルで集計したいと思います。そうすると、アジアの割合が2016年に大きく増えていることが確認できます。もしかすると、大陸レベル何らかのトレンドがあるのかもしれません。
大陸を予測するモデルをつくって、大陸を予測するえで重要な変数を確認する
データの分布は理解できたので、次はいよいよ大陸毎を予測するモデルをつくってどの変数重要度が高いかを見ていきます。上記を検討するうえで、今回は大陸毎にどんな特徴があるかを知りたいので、RankingやTotal scoreは除外していきます。
加えてInternational ScoreとInternational_student_ratioとの間に強い相関があったので、International score は説明変数から抜きます。
※Internatinal_students_ratioは新たにつくった列です。
年ごとに傾向が違うこともありうるかと思ったので、年ごとにモデルも作成しました。
年ごとに大きく傾向が変わっていることはなさそうなので、以降は年は考慮に入れず、下記、上位4つの変数に絞って深掘りしていきたいと思います。
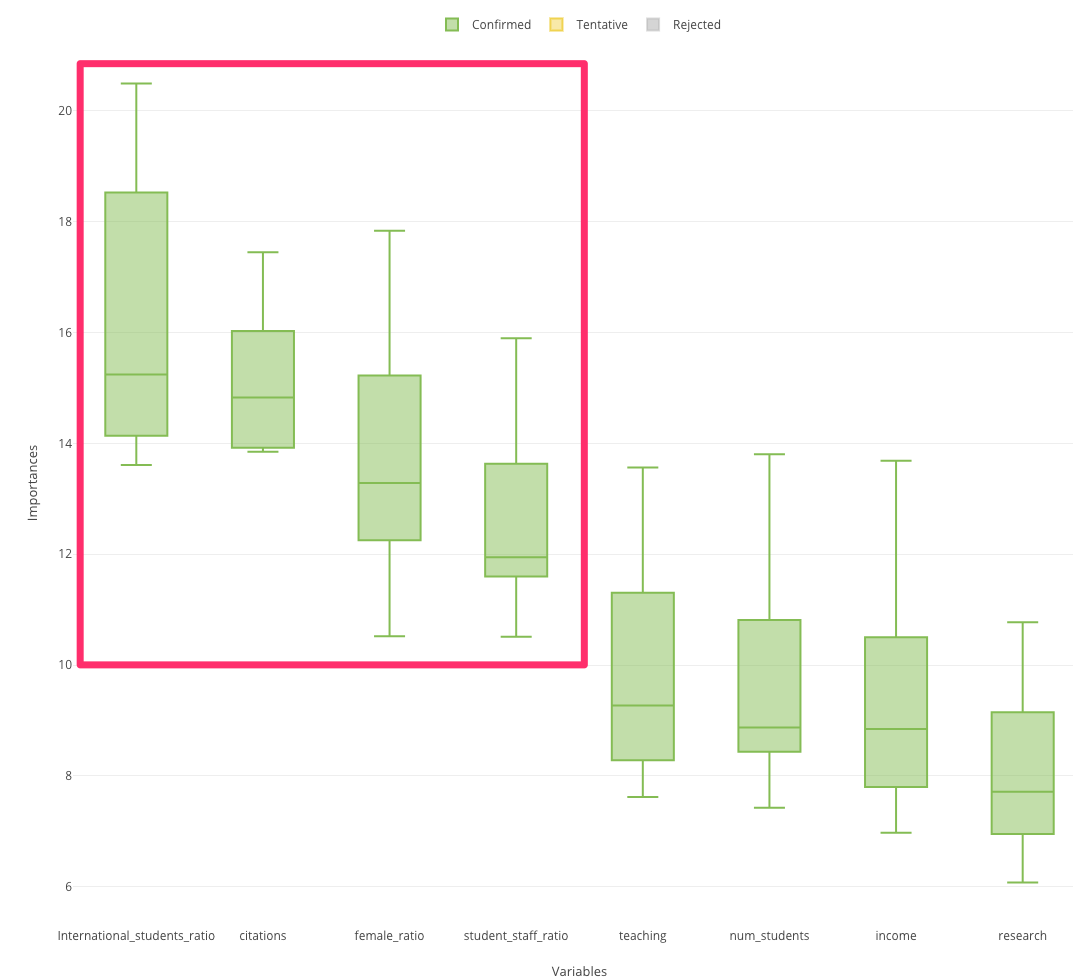
変数重要度の高い変数に絞って、箱ヒゲ図で可視化する
今回注目した4つの変数は指数型の分布は特にしていないので、各変数を正規化したうえで、バイオリン図でどのような分布になっているか可視化していきたいと思います。
結論
一見すると差がないように見えますが、例えばfemail_ratioに絞って見てます。
そうするとSA(南アメリカ)の女性比率が他大陸と比べると、低いように見受けられ、AS(アジア)の大学も若干女性比率が低めに分布しているように見受けられます。母数が少ないということもあるかと思いますが私の想像とは異なり、AF(アフリカ)の女性比率SAやASと比べ高めに分布しているようです。
今度はinternational_sutdents_ratioに注目して見ていきます。
そうすると、AF(アフリカ)・AS(アジア)・SA(南アメリカ)の大学はEU(ヨーロッパ)NA(北アメリカ)と比べるとinternational_ratioが低いように見受けられます。
今回は4変数にしか注目はしていませんが、SA(南)においてランキング入している大学は他大陸と比べfemale_ratioやinternatinal_students_ratioが低いという特徴を持っているということが言えそうだということが分かりました。