
ベイジアンA/Bテストの使い方
ビジネスマンが理解できるA/Bテストのフレームワーク
A/Bテストについて聞いたことがある方も多いと思います。A/Bテストとは、AとBの2つのグループを作成し、各グループのパフォーマンスを測定して、どちらがよりパフォーマンスが優れているかをテストすることです。
Webサイトのランディングページに2つのバージョンを用意し、より多くの訪問者がサービスにサインアップするのに役立つページを確認したいとします。
そして、テストを開始してから一週間後に下記のような結果が得られたとします。
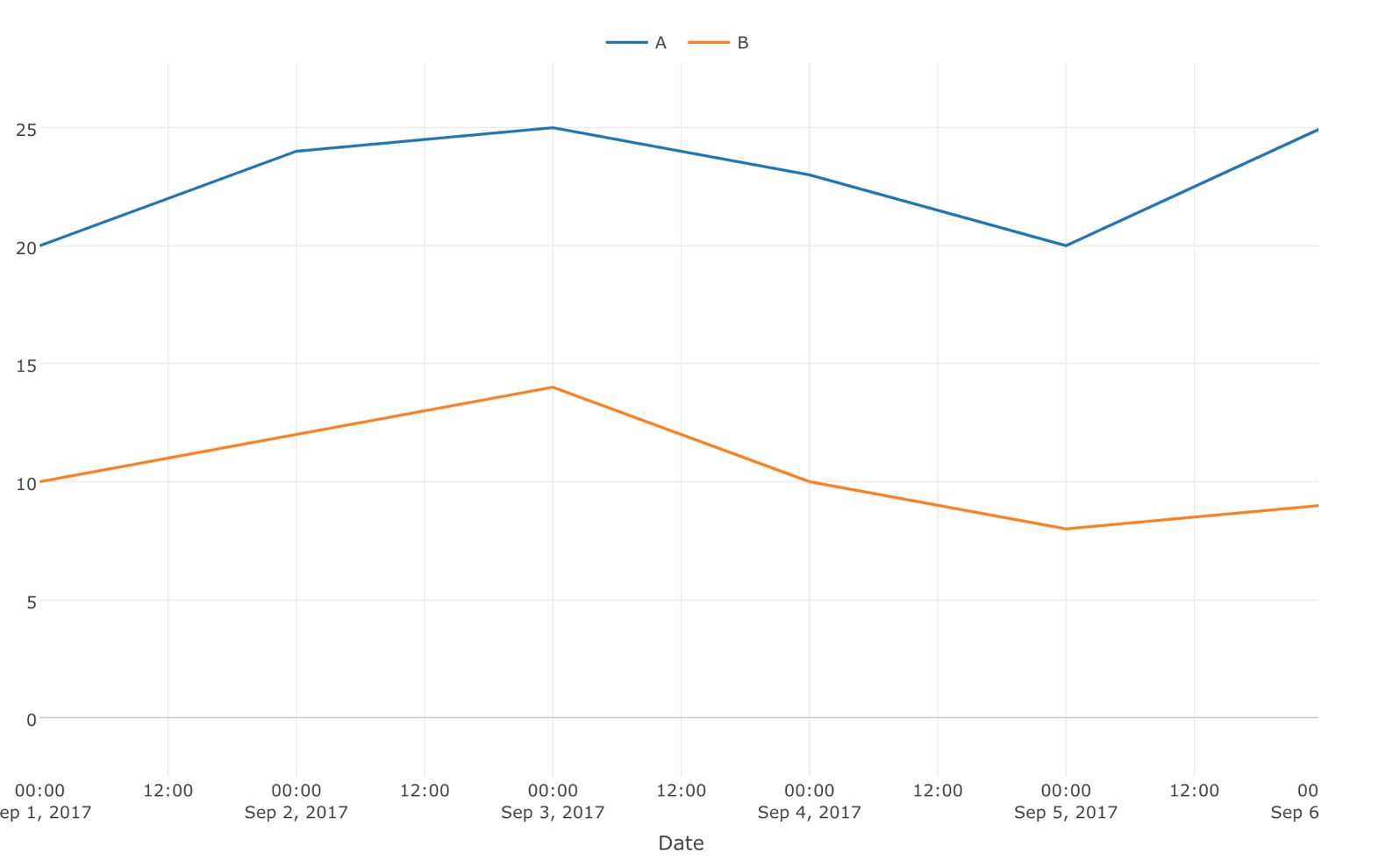
この2つの違いは明白です。
A(青色)は一貫してB(オレンジ色)よりもはるかに優れたパフォーマンスを発揮しています。
しかし、現実の世界で明確に違いが出るということはなかなかありません。AとBの結果は日によって逆転することもあり、次のようになります。
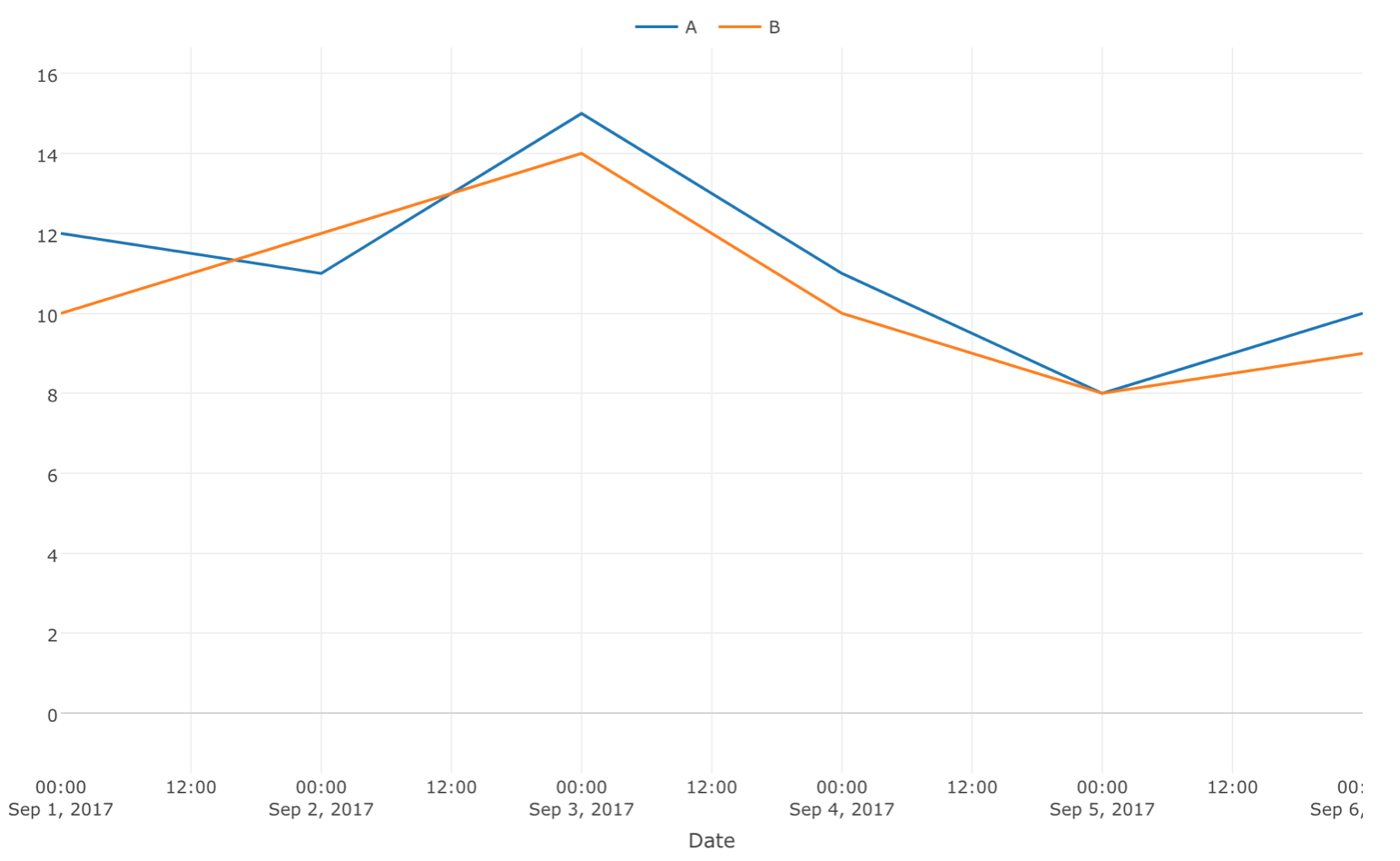
これを見ただけで、AはBよりも優れているように見えるかもしれません。しかし、Bの1日目はAよりも優れており、AがBよりも優れている日でも差は非常に小さいためです。
さて、この結果に基づいてAを選択することに抵抗はありますか?明日はBの方がAよりもパフォーマンスが低いと言ってもいいですか?Aを使用することを決定すると、開発、設計、展開などに追加の時間と費用がかかるとしても、得られる効果の方が高いと言えますか?
したがって、AがBよりも実際に優れていることを確認する必要があります。
ここで統計の出番です。
一般的な方法は2つあります。1つは「カイ二乗検定」と呼ばれる頻度論的方法であり、もう1つは「ベイジアンA/Bテスト」と呼ばれるベイズ統計の方法です。
このノートでは、A/Bテストという観点でカイ二乗検定がどのように機能するか、およびこのアプローチで直面する課題について説明します。次に、A/Bテストの結果を評価するための別のアプローチとして、ベイジアンA/Bテストを紹介します。
ただし、その前に、どちらの方法を使用するかに関係なく、最初にデータを準備する必要があります。ベイジアンA/Bテストの仕組みに興味がある場合は、次のセクションをスキップしてください。
データの準備
ランディングページの2つのバージョンをテストし、各ページが毎日どのくらいの「サインアップ」に効果があるのかをモニタリングしているとしましょう。
こちらにサンプルデータをアップロードしました。CSVとしてダウンロードできます。
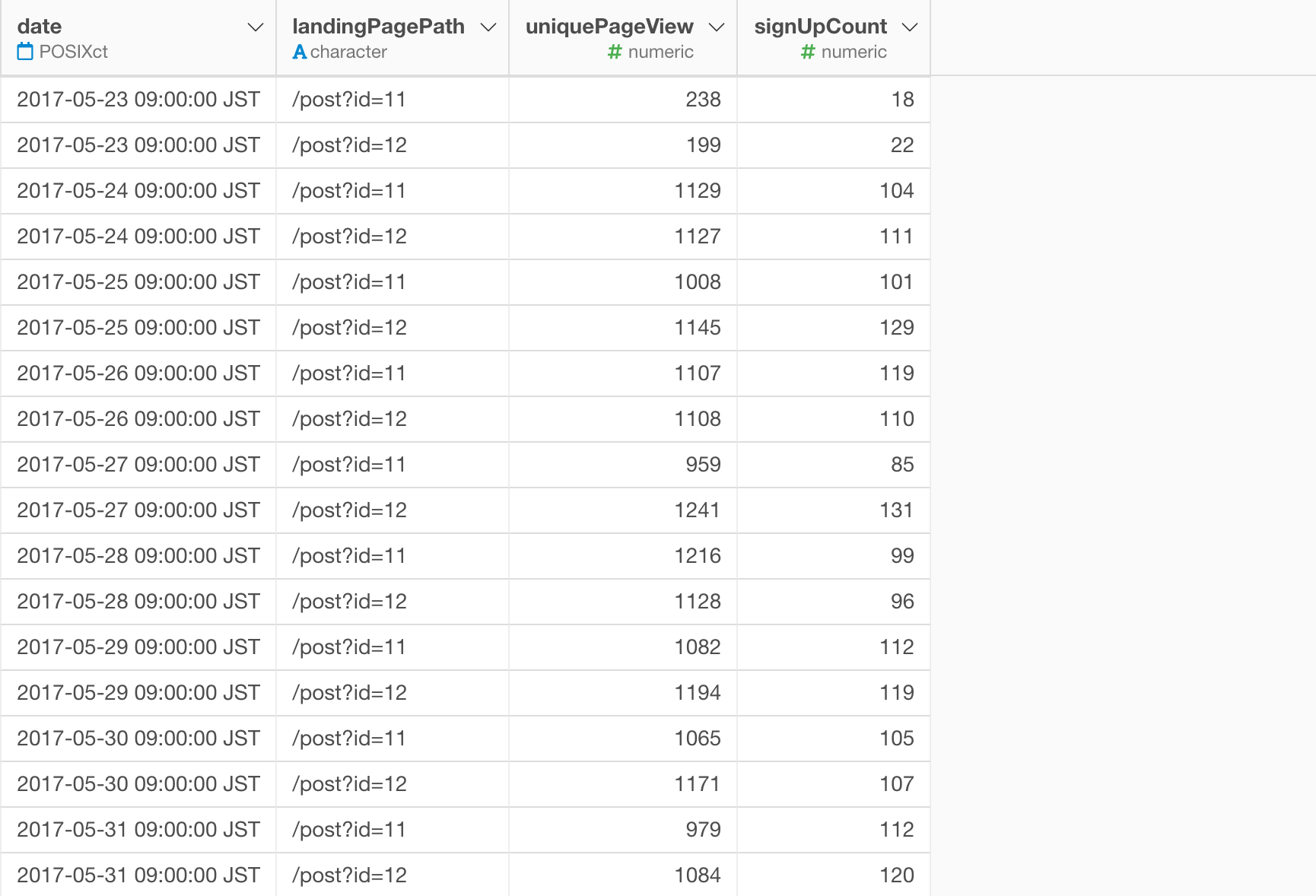
これは、次の列を使用して日付レベルで集計されます。
- date - 1日単位の日付
- landingPagePath - ランディングページとして2つのページがあり、ABテストで比べたい対象です。
- uniquePageView - 各ランディングページの一意のページ閲覧数
- signUpCount - 最終的にサインアップした数。
カイ二乗検定またはベイジアンA/Bテストを実行するには、データに2つの前提条件があります。
まず、サインアップした数だけでなく、「サインアップしていない数」もデータとして持つ必要があります。
以下のように、サインアップ数とサインアップしていない数を別々の列として持つのではなく、一つの列にサインアップしたか、していないかの情報をまとめます。このことをデータをロング型(縦長のデータ)にすると言います。
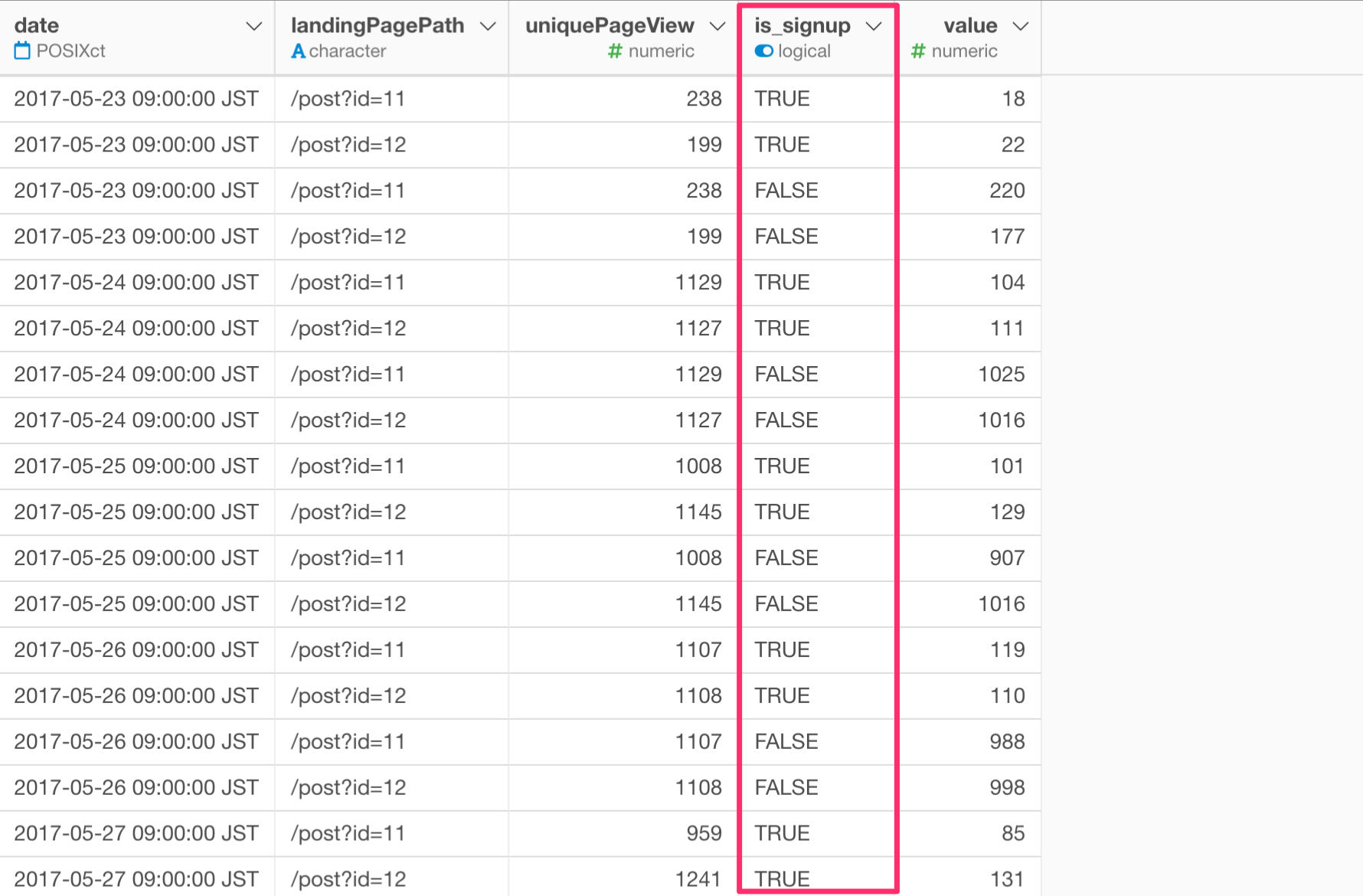
dateをみてみると、以前は「2017–05–23」は2行しかありませんでしたが、4行になりました。これは、ランディングページのIDごとにサインアップしたかどうかの行が設定されているためです。
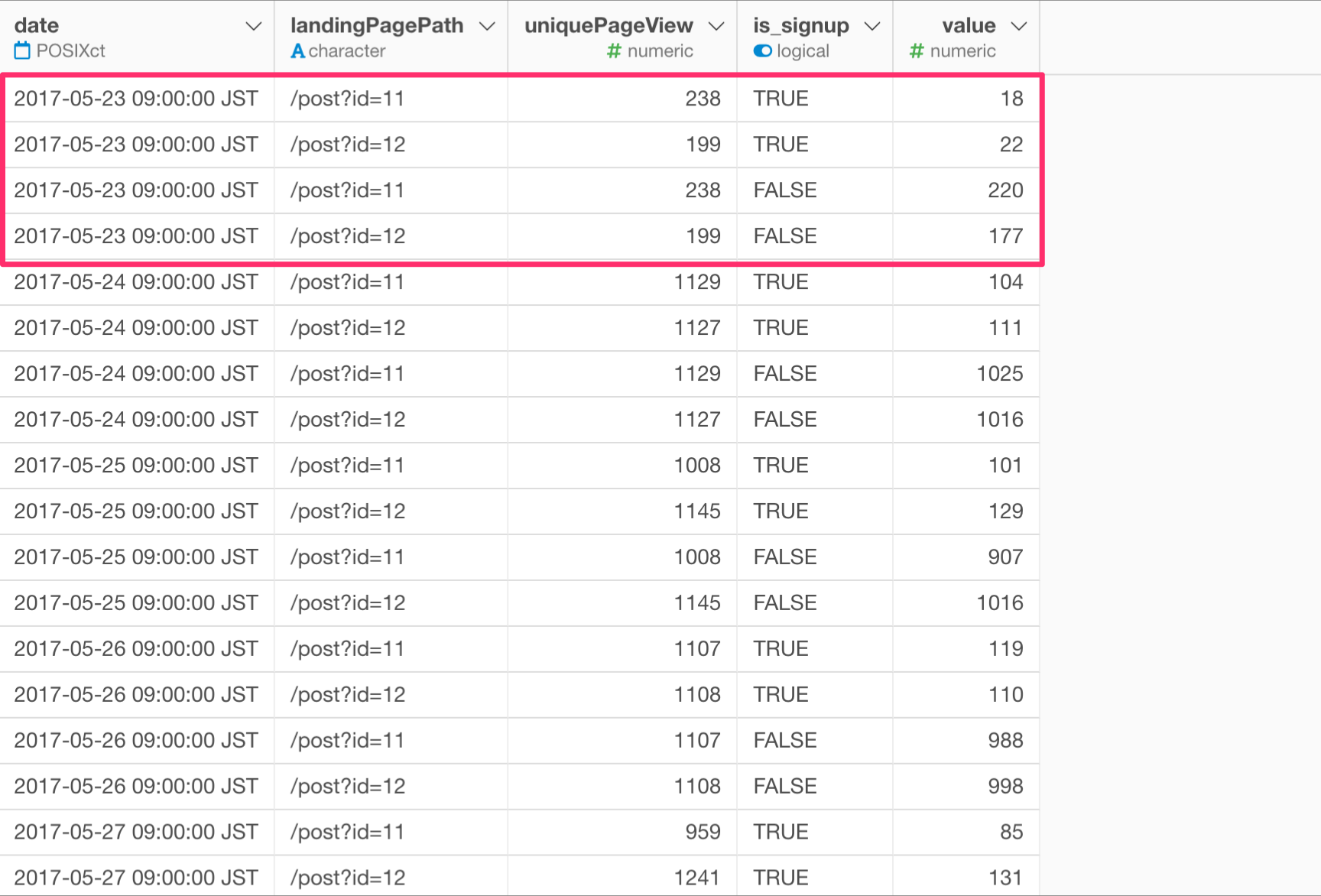
この形式のデータが準備できたら、カイ二乗検定またはベイジアンA/Bテストのいずれかを実行することができます。この形式のデータがすでにある場合は、次のデータラングリング(データの加工)のセクションをスキップしてください。
ただし、ほとんどの場合、特にGoogle Analyticsなどの一部のサービスからデータを取得する場合は、データがこの形式であることはありません。
このデータを取得するには、次の3つの手順を実行する必要があります。
- サインアップしていない数を計算して新しい列を作る。
- サインアップ数とサインアップしていない数を一つの列にまとめ、'is_signup'列として、 「Sign Up」または「Non-Sign Up」のラベルをつける。
- 'is_signup'列をcharacter型ではなくlogical型にする。
1. サインアップしていない数を計算して新しい列を作る。
下記が元のデータになります。
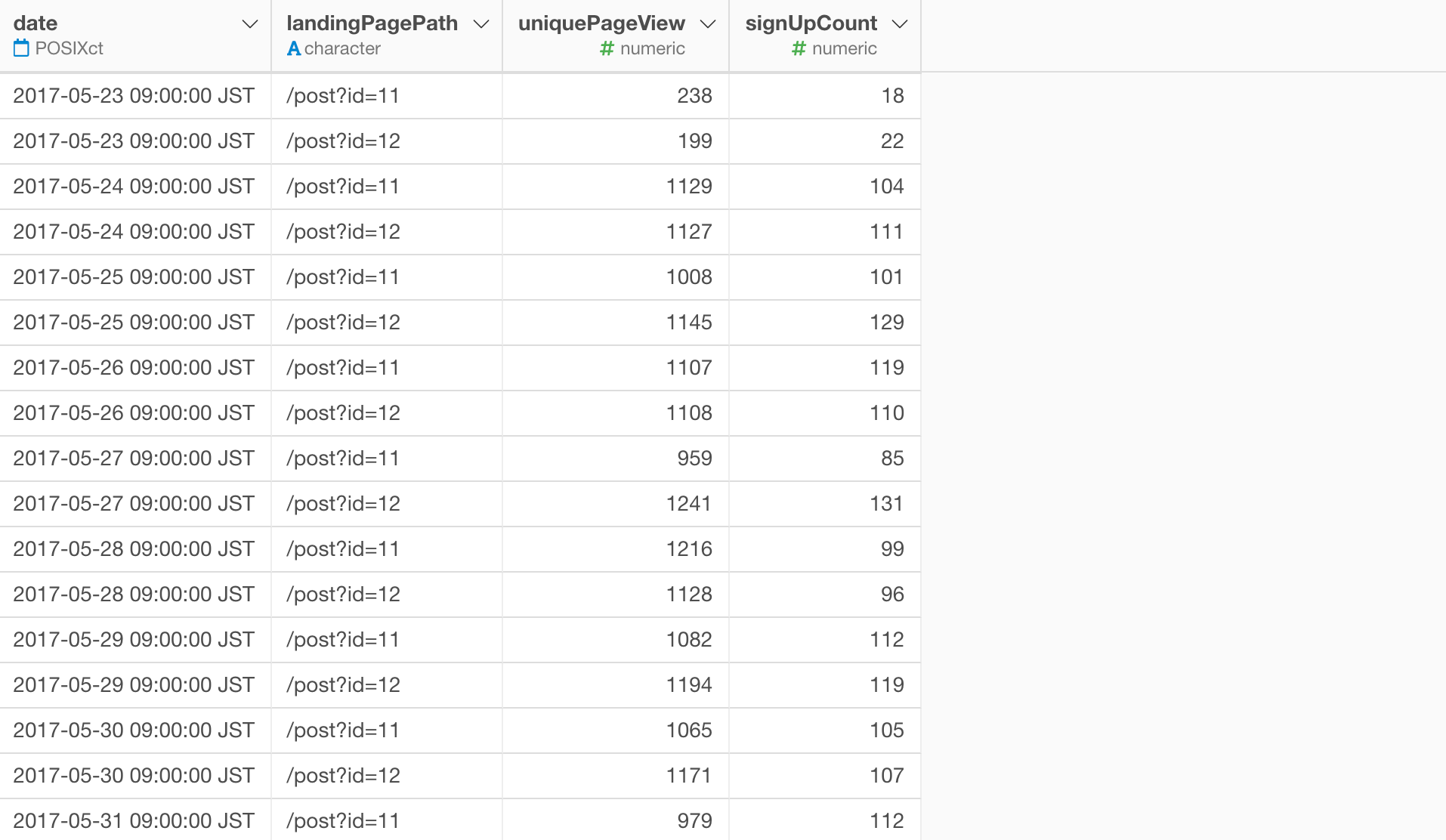
サインアップしていない数は、UniquePageViewからSignUpCountの数を引くことで求めることができます。
列ヘッダーメニューから「計算の作成(Mutate)」を選択します。
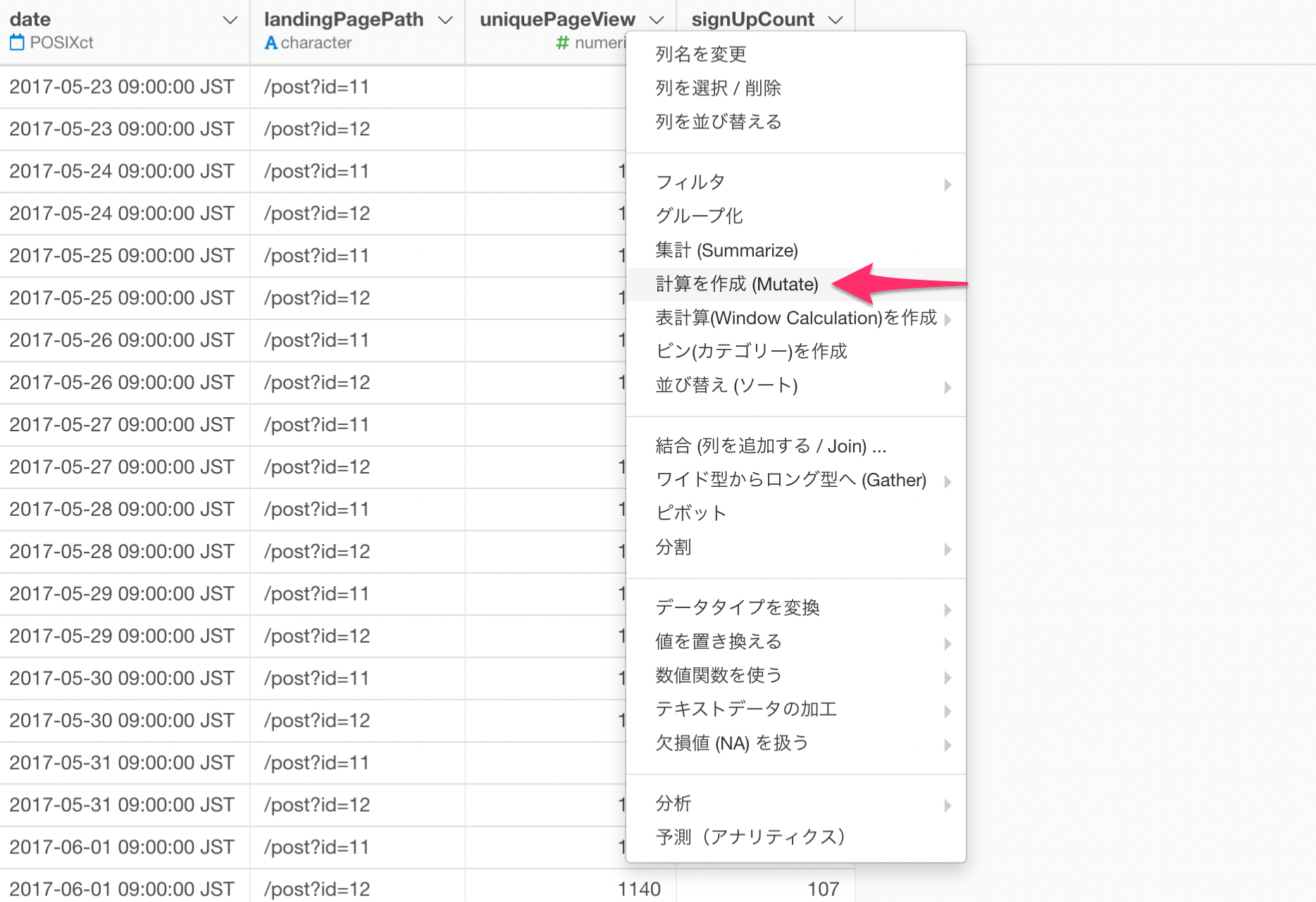
そして、次の計算式を入力します。
uniquePageView - signUpCount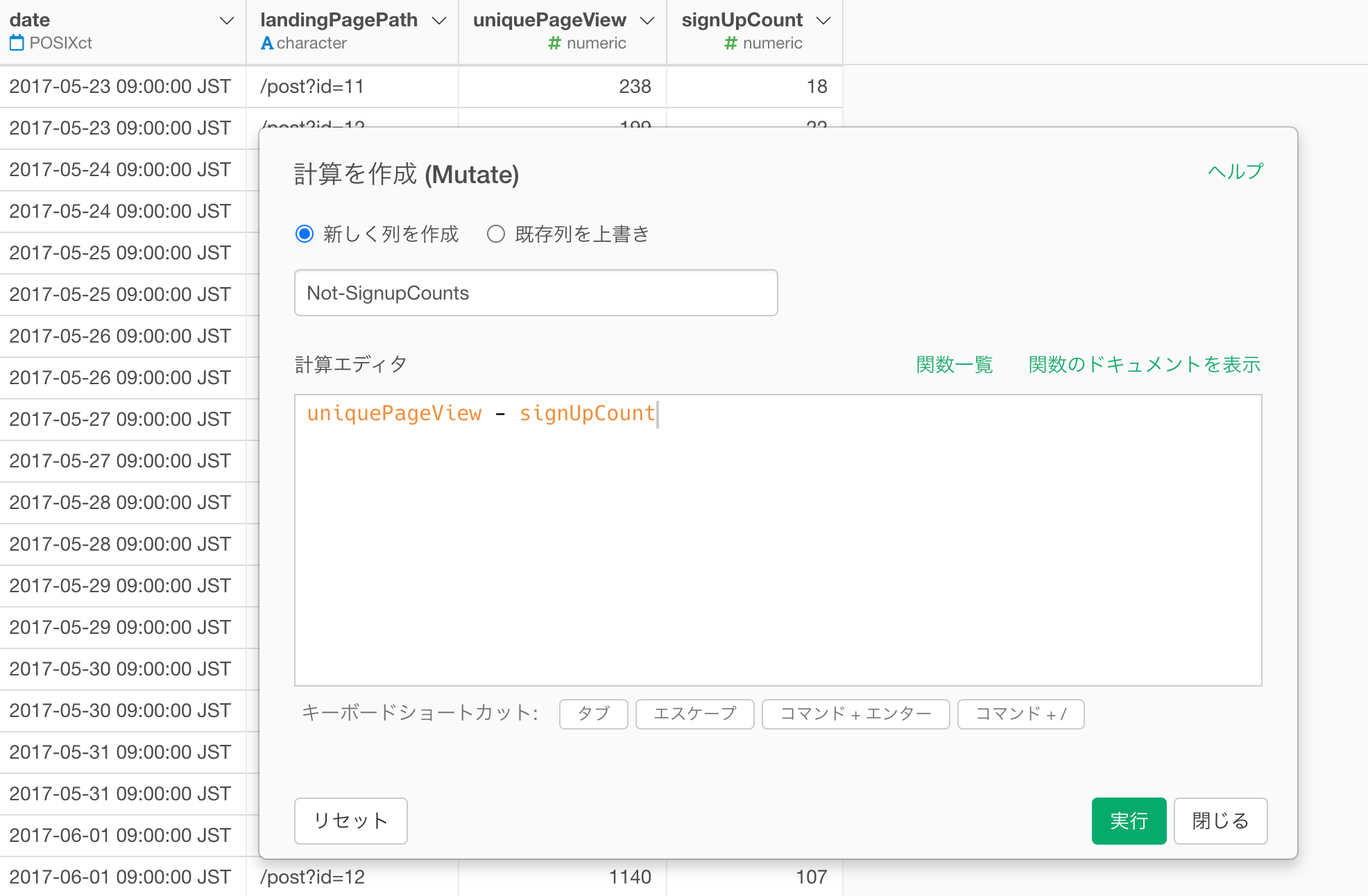
これにより、サインアップしていない数が求められました。
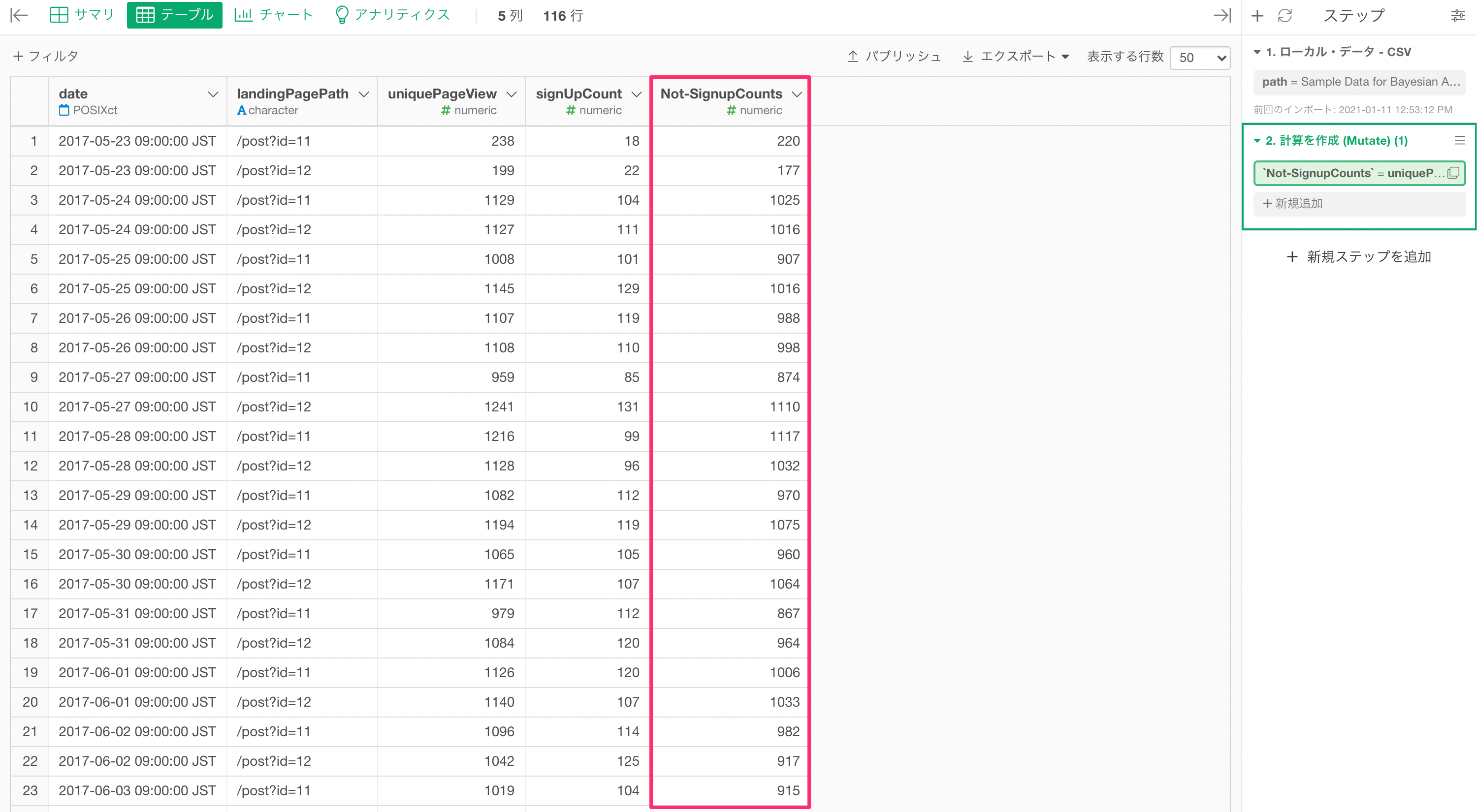
2.「サインアップ数」と「サインアップしていない数」を一つの列にまとめる
「サインアップ数」と「サインアップしていない数」が別々の列としてありますが、数値を一つの列にまとめ、サインアップかサインアップしていないかを示す列が必要です。
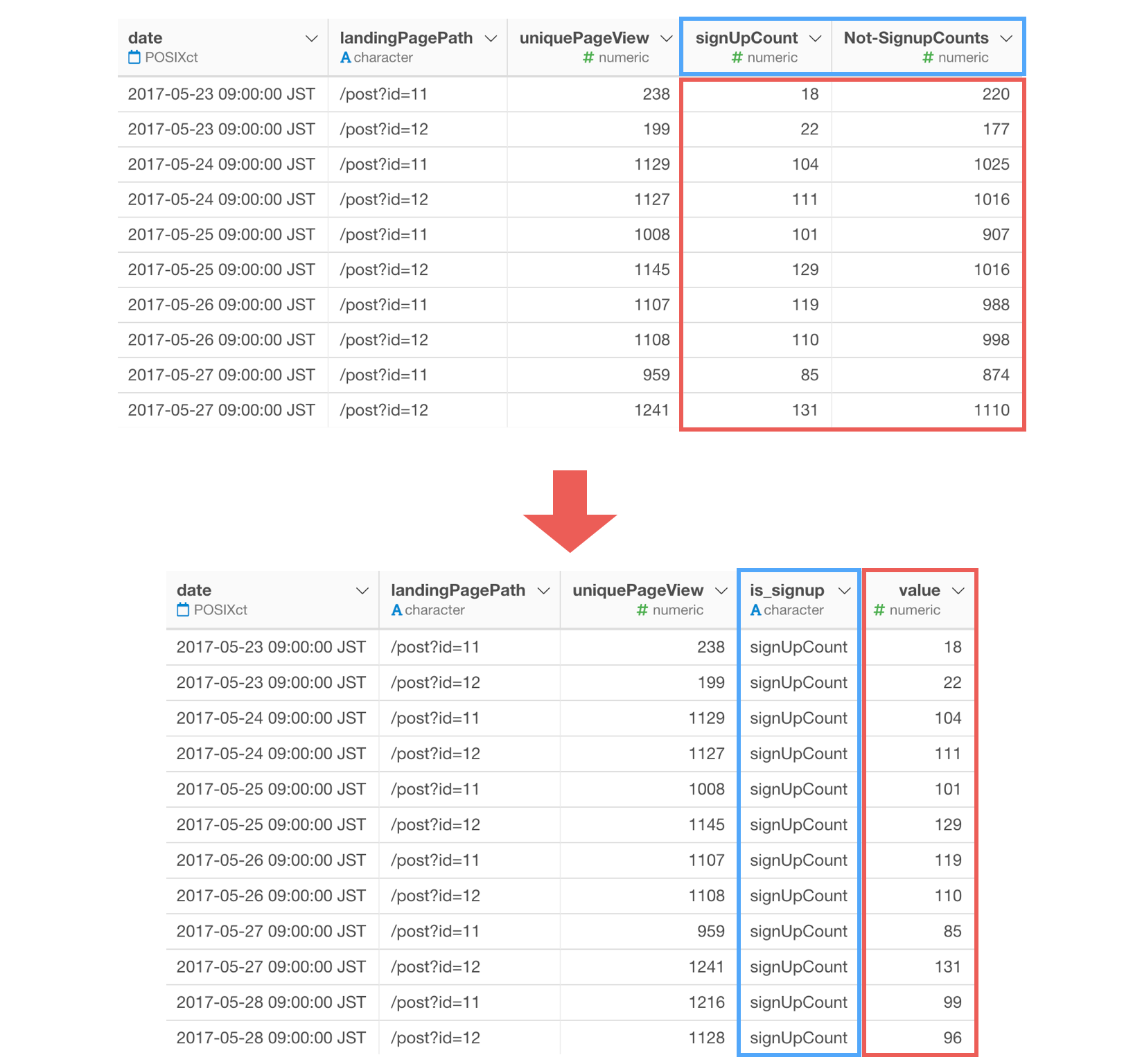
そこで、「tidyr」パッケージのGatherというコマンドを使用することで、ワイド型からロング型へ変換することができます。ExploratoryではこのGatherというコマンドを書く必要はなく、UIから実行できます。
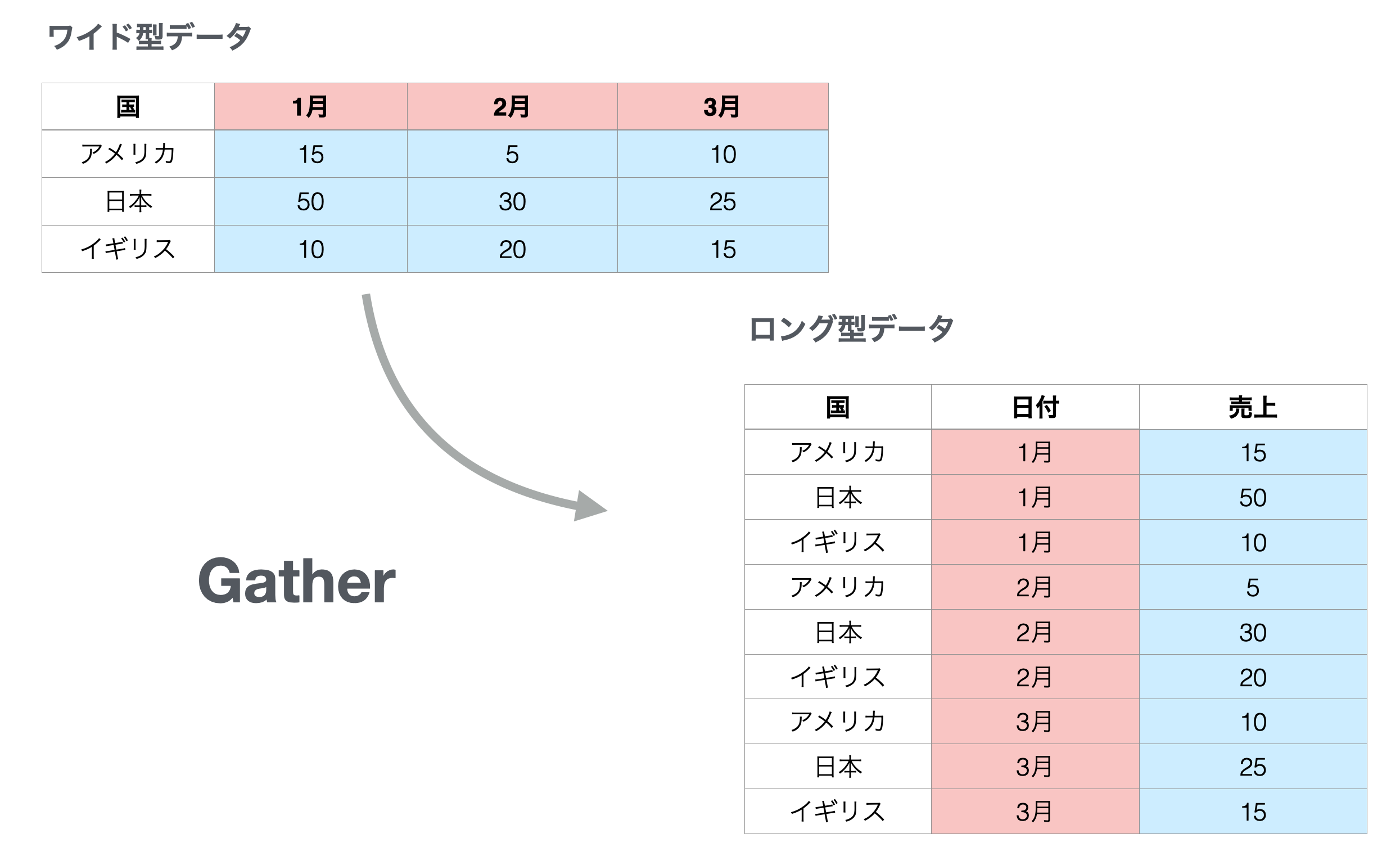
Command(またはControl)キーを使用して「SignUpCount」列と「Not_signUpCount」列を選択し、列ヘッダーメニューから「ワイド型からロング型へ(Gather)」を選び、「選択された列」をクリックします。
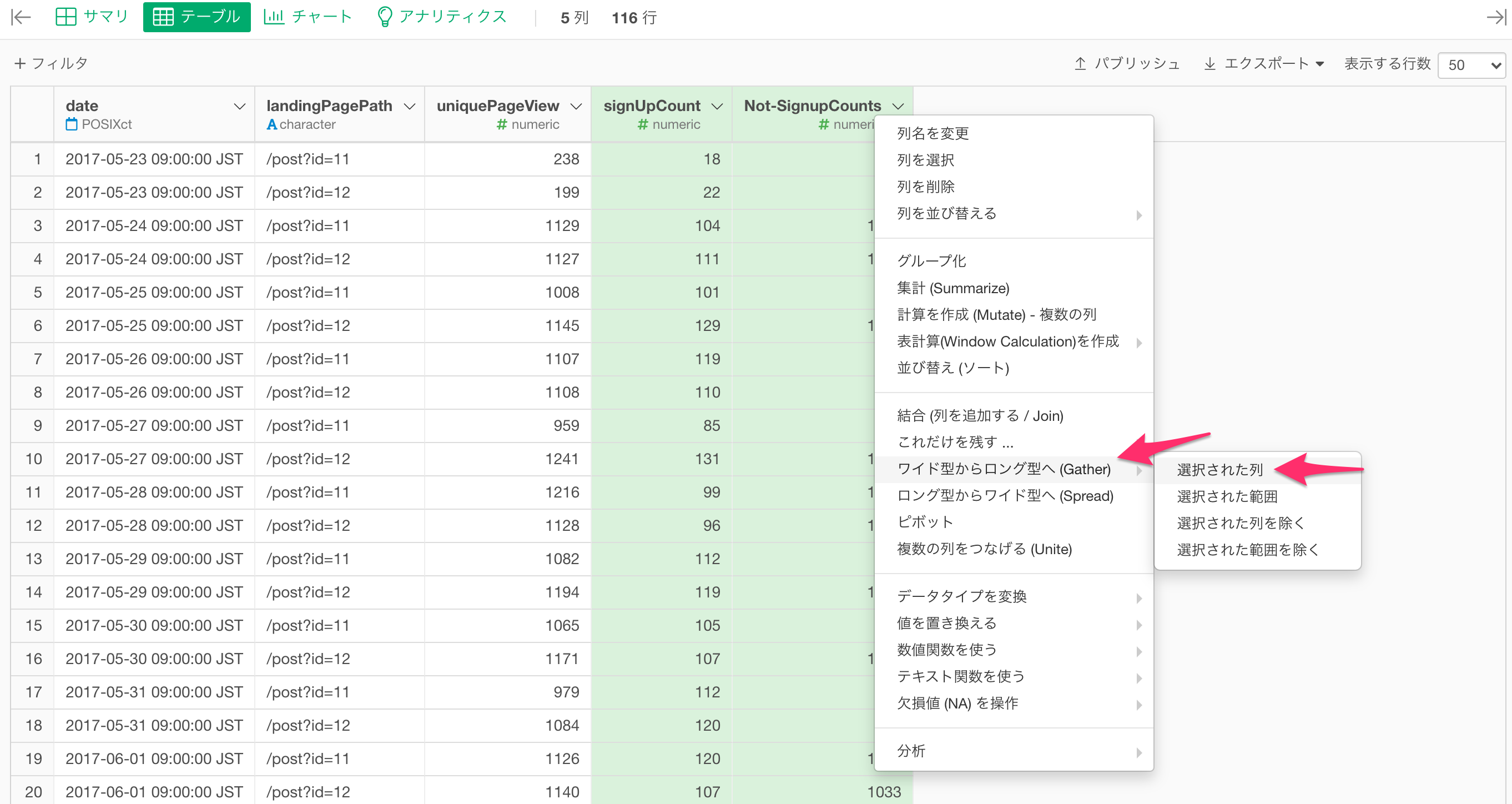
ワイド型からロング型へのダイアログ上で、キー列に「is_signup」、値の列に「value」を指定します。
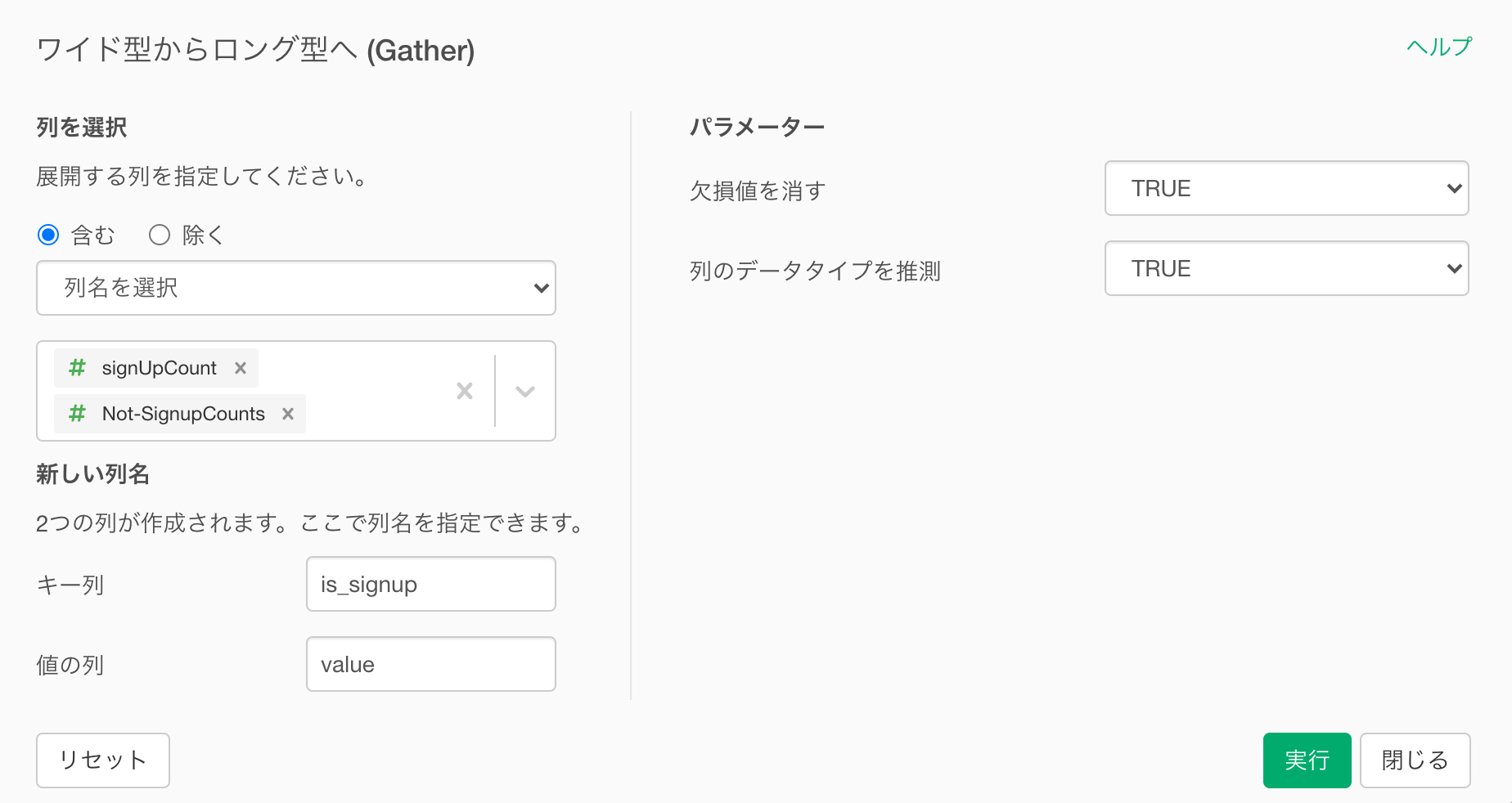
実行すると、元の列名が「is_signup」列の値となり、サインアップ数とサインアップしていない数の値は「value」列にまとめられていることが確認できます。
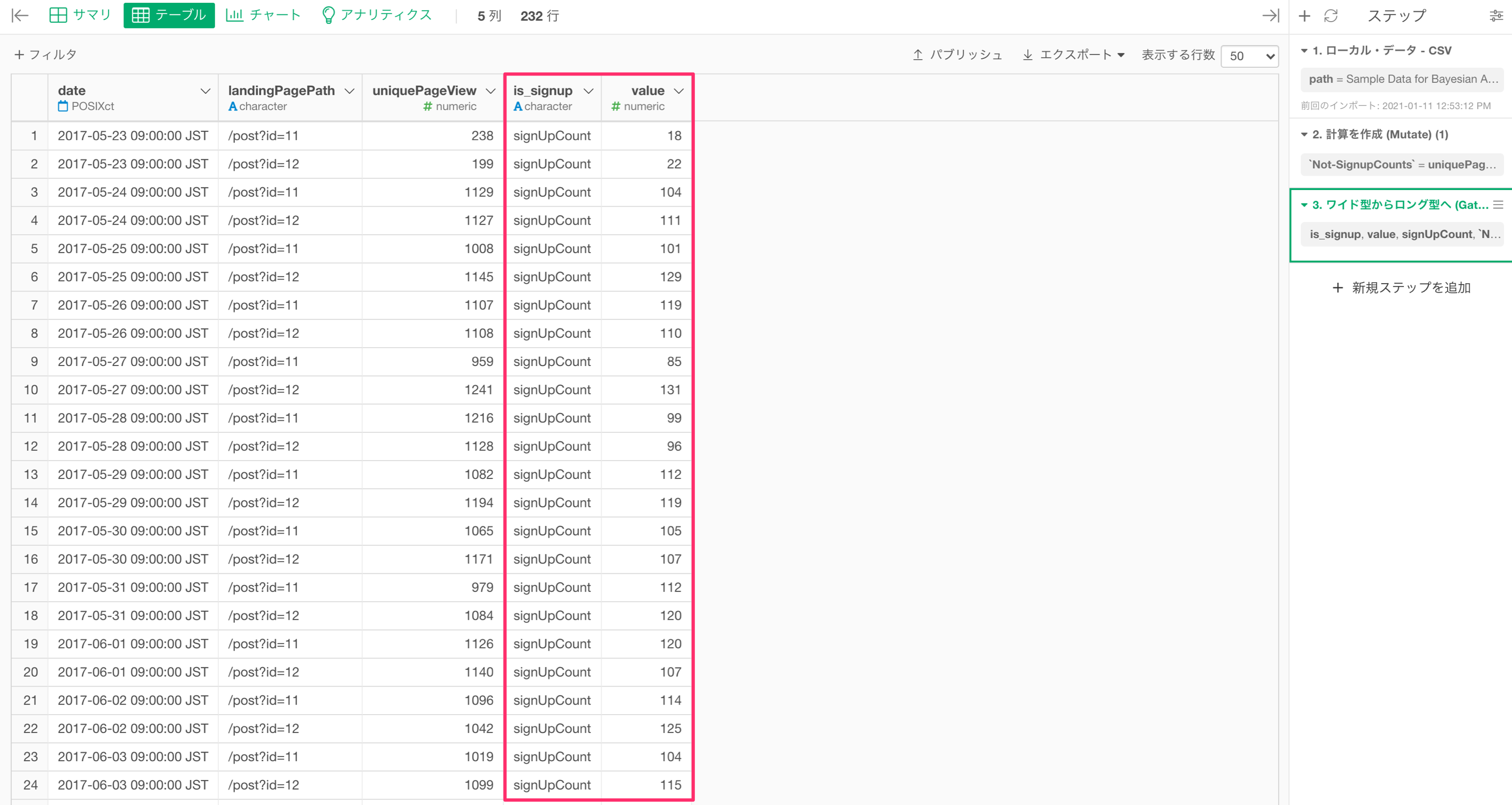
3.is_signup列をcharacter型ではなくlogical型にする。
is_signup列をlogical型(論理値)に変換せずに、カイ二乗検定またはベイジアンA /Bテストを実行できます。しかし、logical型にすることで、値がTRUEまたはFALSEになり、結果を解釈しやすくなります。
列ヘッダメニューから計算を作成を選択します。
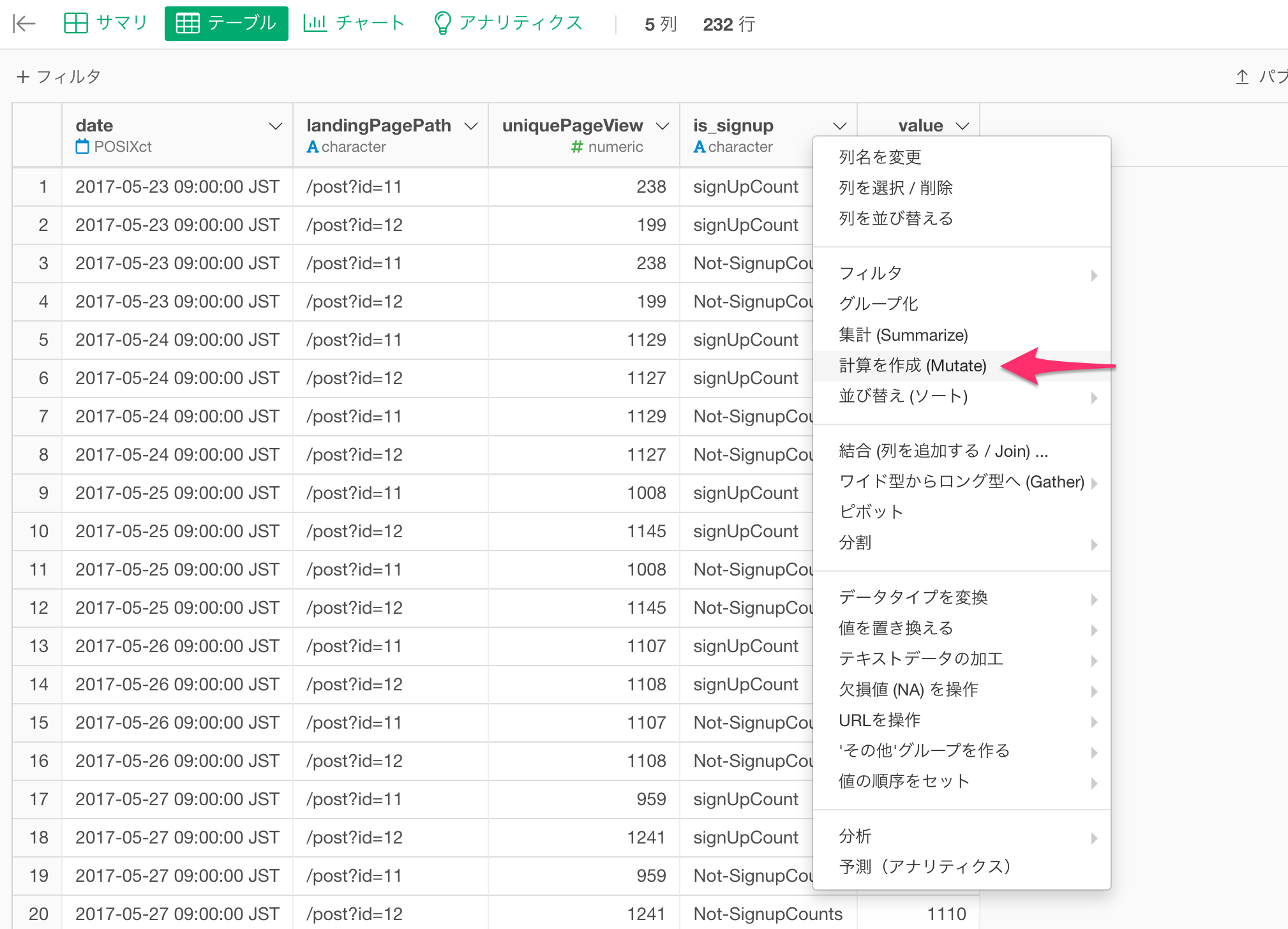
そして、計算エディタに下記の条件を入力して、既存列に上書きにチェックをして実行します。
is_signup == "signUpCount"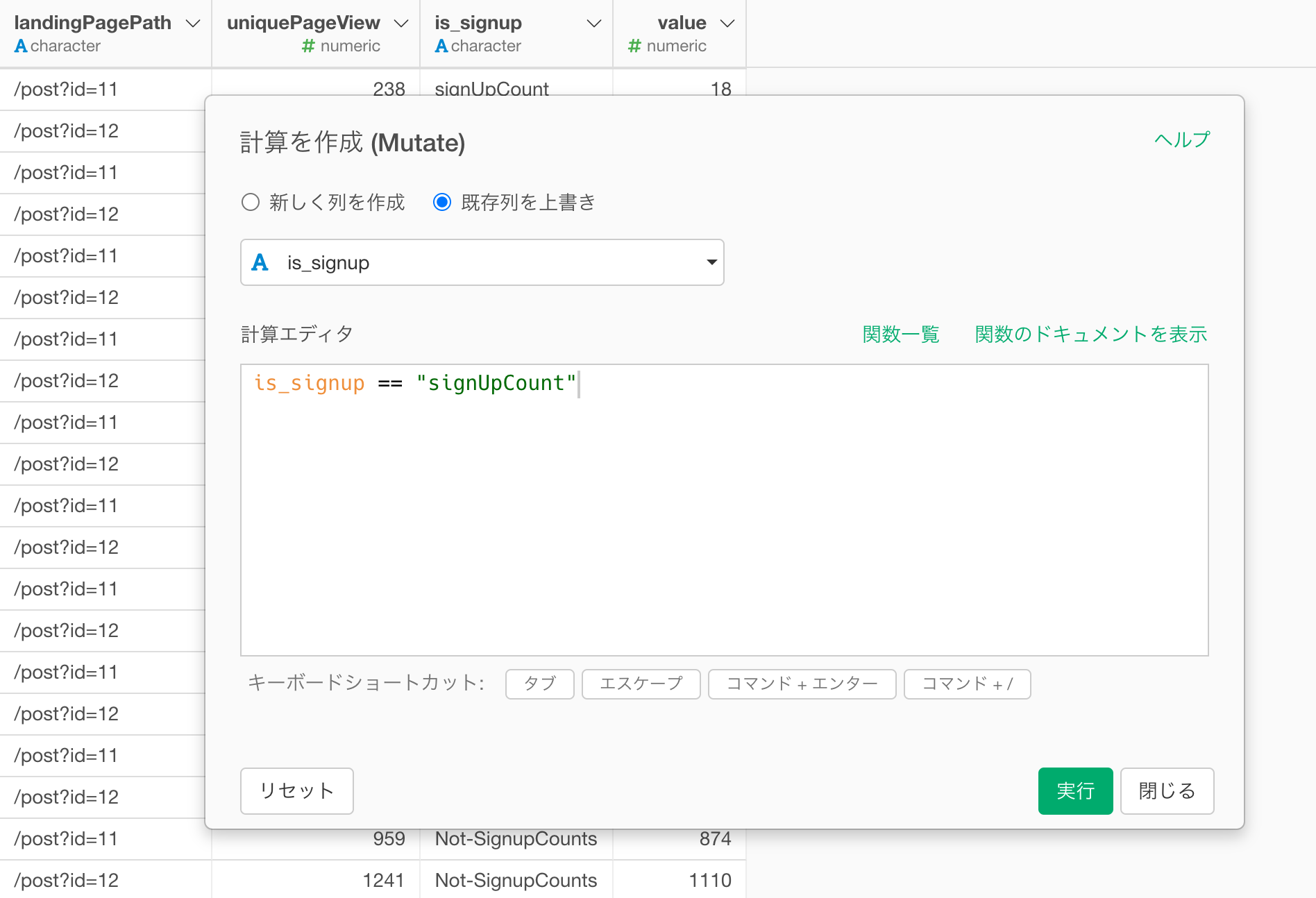
これにより、値が「singUpCount」の場合はTRUEを返し、そうでない場合はFALSEを返します。
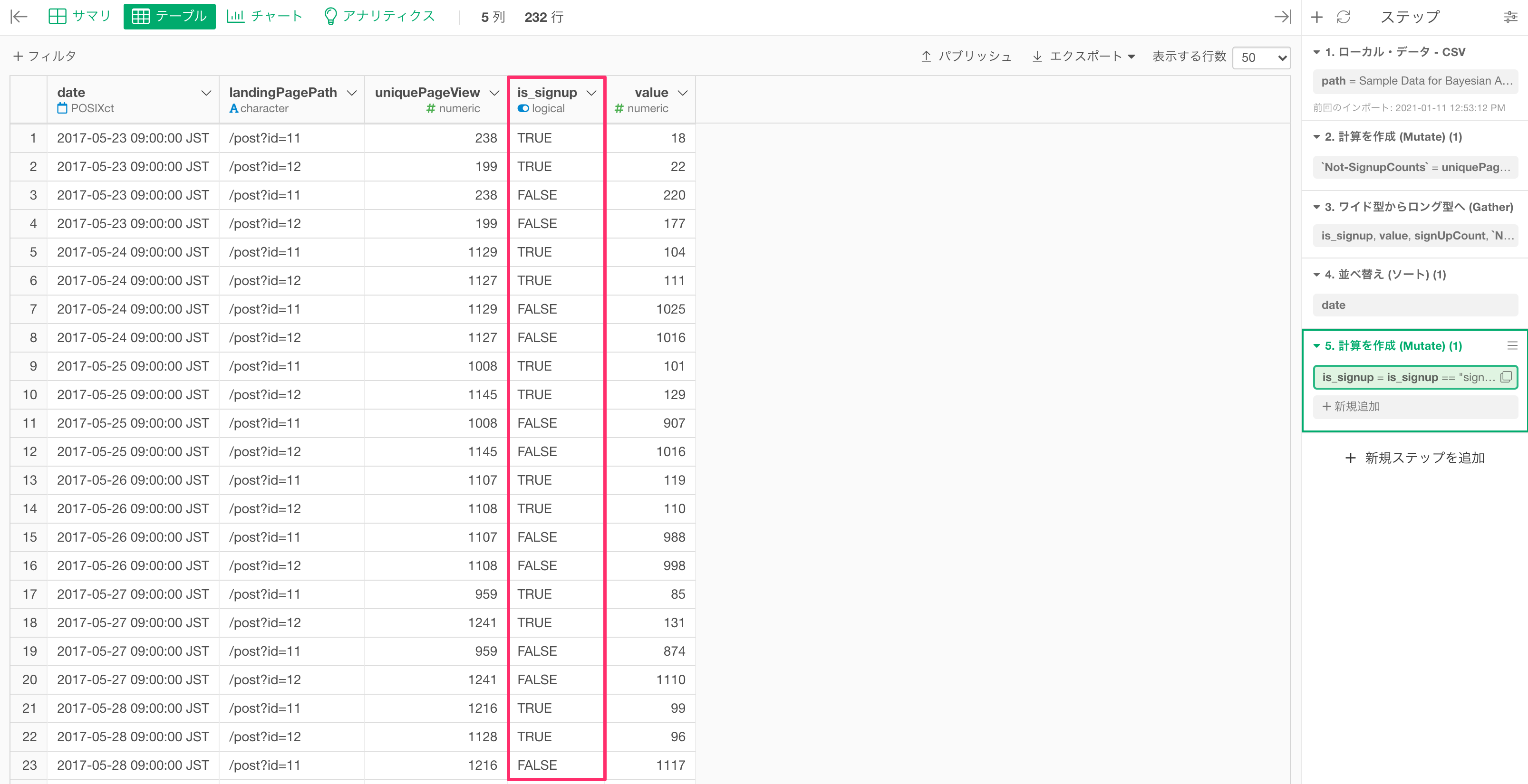
これでデータの準備ができました!
カイ二乗検定
カイ二乗検定を実行するには、アナリティクスビューに移動し、タイプからカイ二乗検定を選択します。
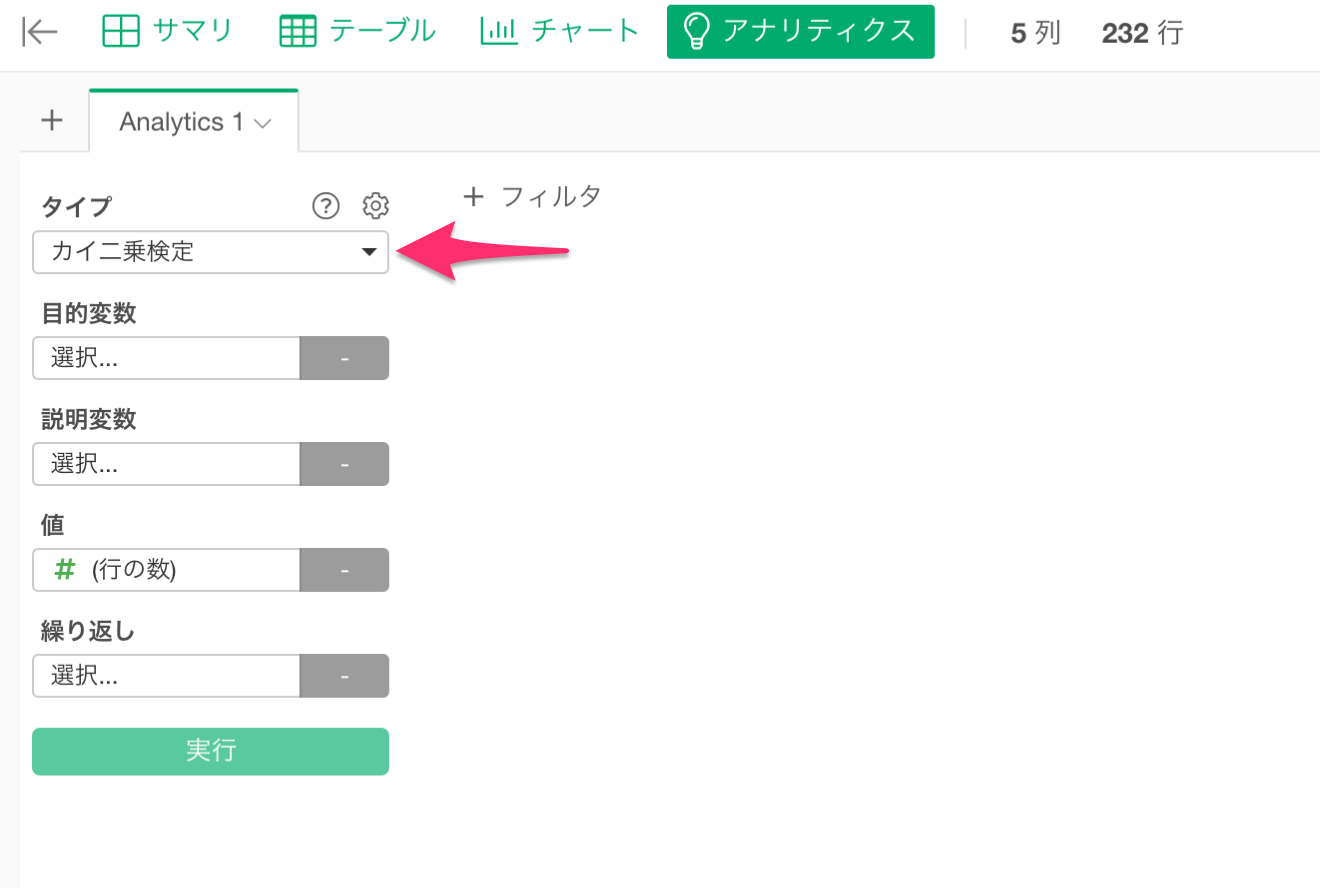
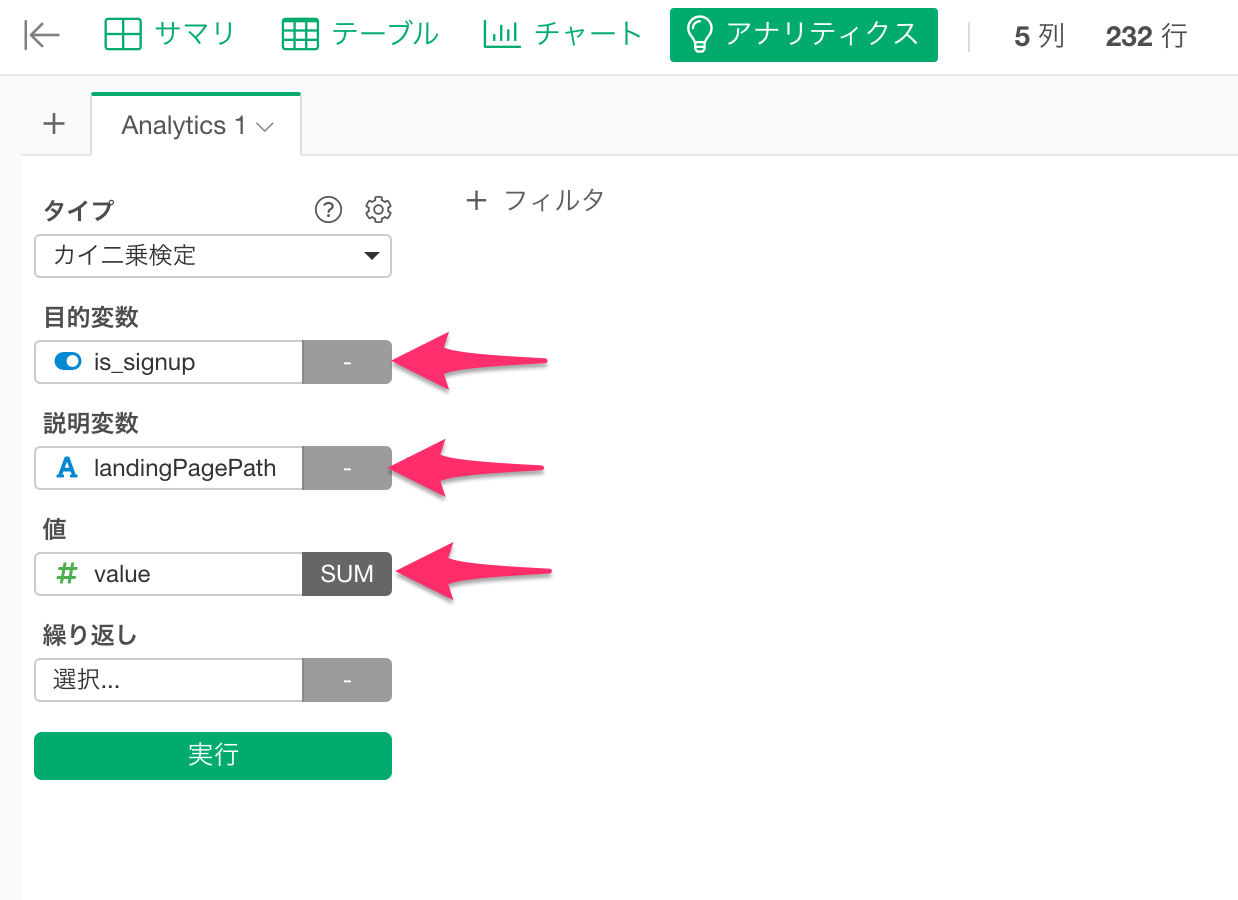
次に下記の列を割り当てます。
- 目的変数にis_signupを選択します。
- 説明変数にlandingPagePathを選択します。
- 値にvalueを選択します。
実行します。
ここで最も重要な情報はP値です。
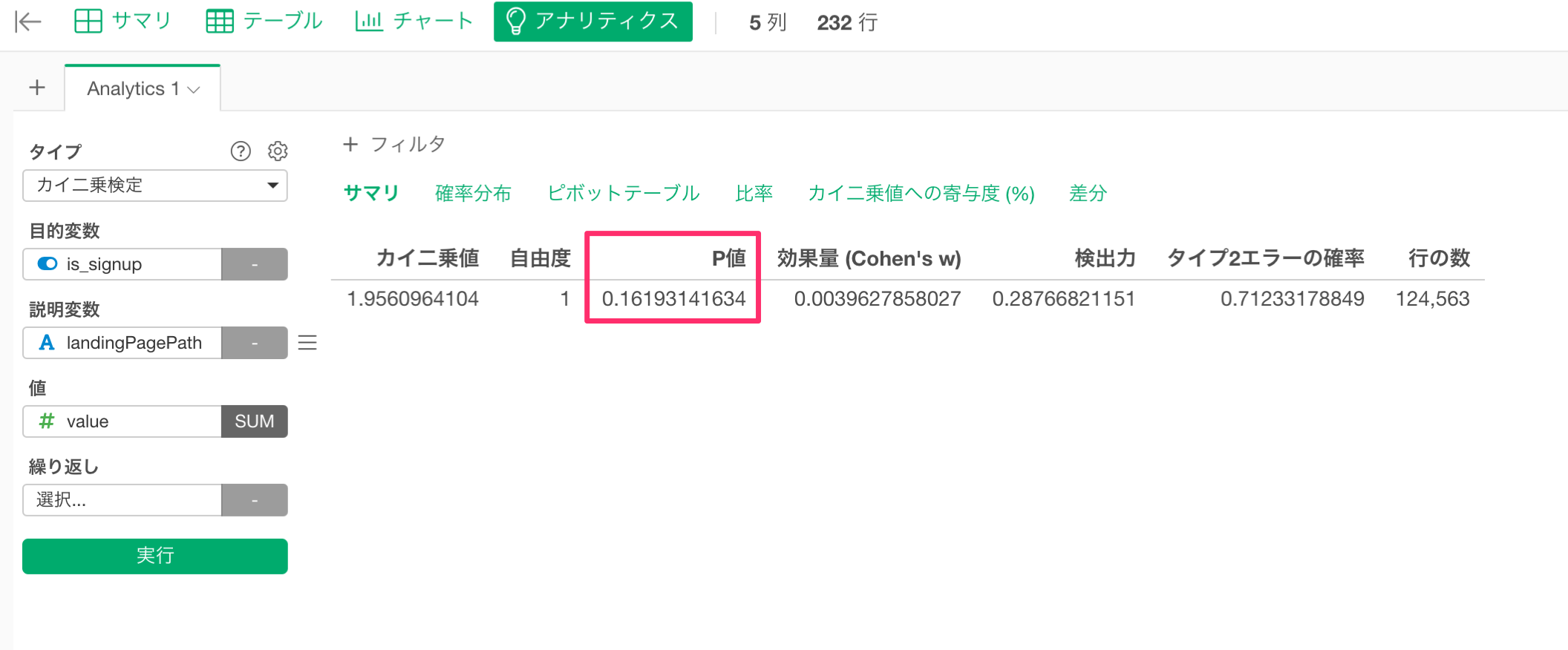
このカイ二乗検定の結果のP値は0.16です。これは、2つのランディングページのサインアップ数の違いが偶然に発生する割合を示しています。
今回の場合、この違いは16%の割合で発生する可能性があることを意味します。
16%は高すぎますか、それとも低すぎますか?
ビジネスや業界が異なれば、P値のしきい値も異なります。しかし、統計的に有意であるか確かめるために、一般的に採用されているしきい値の5%で設定したとします。その場合、16%だとしきい値を超えた値となり、これら2つのランディングページの違いは統計的に有意であるとは言えないという結論になります。
この結果からどうすればいいのでしょうか。もう一度テストをするべきなのでしょうか?それとも違いが無いと結論付けますか?
これは、カイ二乗検定でABテストをする際に直面する課題の1つです。カイ二乗検定を使用する際に起こる課題は他にもあります。
- テストを開始する前に、収集する必要のあるデータの量を知る必要がある。
- 結果をリアルタイムで評価することができない。また、事前に計画したデータ量になるまで、判断できない。
- テストの結果は、統計学を知らない人にとっては直感的に理解しづらい。
これらの課題に関心がある場合は、ベイジアンA/Bテストを試してみることをお勧めします。
ベイジアンA/Bテスト
ベイジアンA/Bテストでは、ベイズ推定を使用して、AがBよりも優れている(または劣っている)「確率」を示します。
この方法の利点は、統計学の知識がなくても、結果を直感的に理解できることです。これは、ビジネスの担当者とのコミュニケーションがしやすくなることを意味します。
もう1つの利点は、結果を評価するときにデータの量についてあまり心配する必要がないことです。AとBの間の一方が他方よりも優れている確率を読み取ることで、初日(または最初の1時間)からテスト結果を評価していくことができます。
もちろん、十分なデータサイズがある方がいいですが、「まだ十分なデータがない」よりも「AはBよりも60%の確率で優れている」と言える方が意思決定が必要なビジネスで役に立ちます。
なぜベイジアンが一般的に使われていなかったのか?
したがって、ベイズ推定のアプローチは企業にとって素晴らしいと言えます。しかし、このアプローチは、カイ二乗検定を含む他のアプローチと比較して、まだまだ人気がありません。
1つの大きな理由は、ベイズ推定のアプローチは様々なパターンをシミュレートすることによって多くの計算が必要になるからです。以前の低スペックのコンピューターでは困難でしたが、中程度の計算能力を備えた今日の最新のPCでは問題ではありません。
ベイジアンを使用する前に何か知っておく必要がありますか?
ベイジアンについて知っておくべきことは2つあります。1つは事前確率(Prior)で、もう1つは事後確率(Posterior)です。事前確率は、基本的にはこれまでのデータについて持っている知識です。たとえば、テストを開始する前に、Webサイトの一般的なコンバージョン率がどの程度になるかを知っている可能性があります。
事後確率には、実際のデータが入ってきた後に更新された知識です。それは以下のようなものです。
Posterior = Data + Priorベイジアンのこれらの用語に精通していないかもしれませんが、概念は非常に単純です。事前確率と事後確率について詳しく知りたい場合は、フランク・ポートマン氏によるこの投稿をご覧ください。
ExploratoryでベイジアンA/Bテストを使用する方法
フランク・ポートマン氏が作成した“bayesAB”というRパッケージがすでにあることです。これは、A/Bテストの結果を評価するために、ベイズ推定を使用した方法を提供しています。
こちらがデータを加工した、ユーザーがサインアップしたかのデータです。
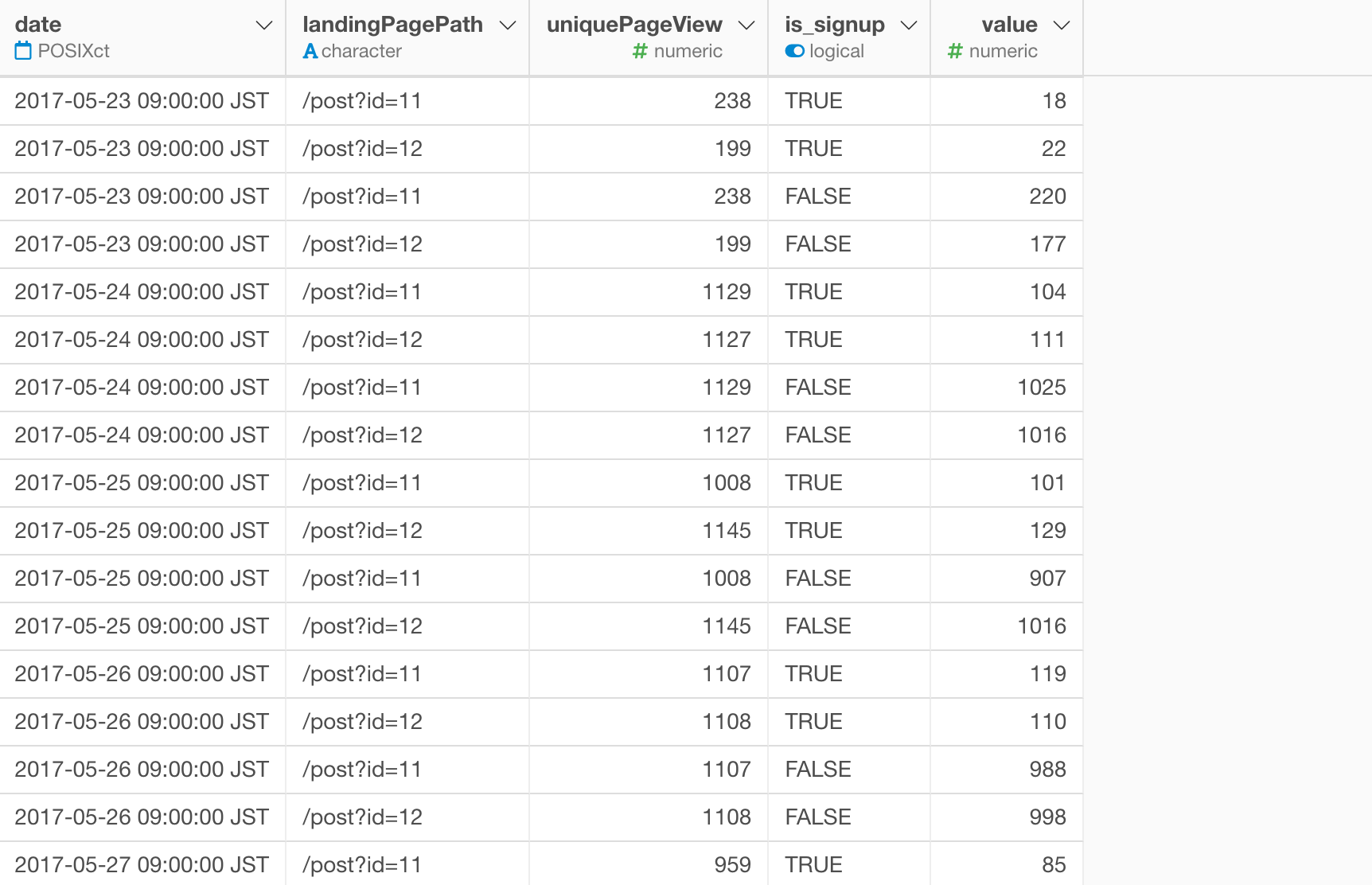
アナリティクスビューから、タイプに「A/Bテスト - ベイジアン」を選択します。
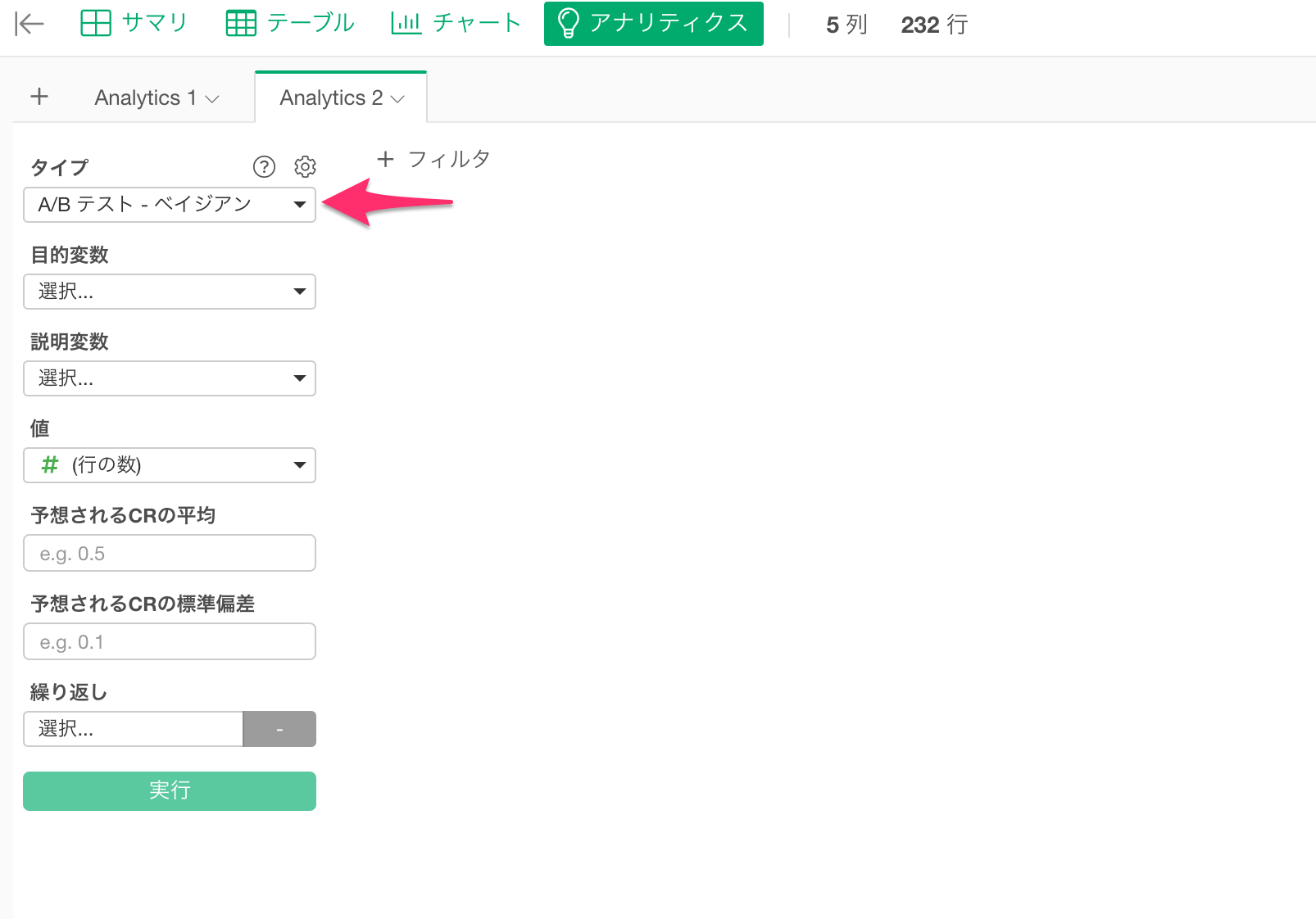
次に、下記に列を割り当てる必要があります。
- 目的変数
- 説明変数
- 値
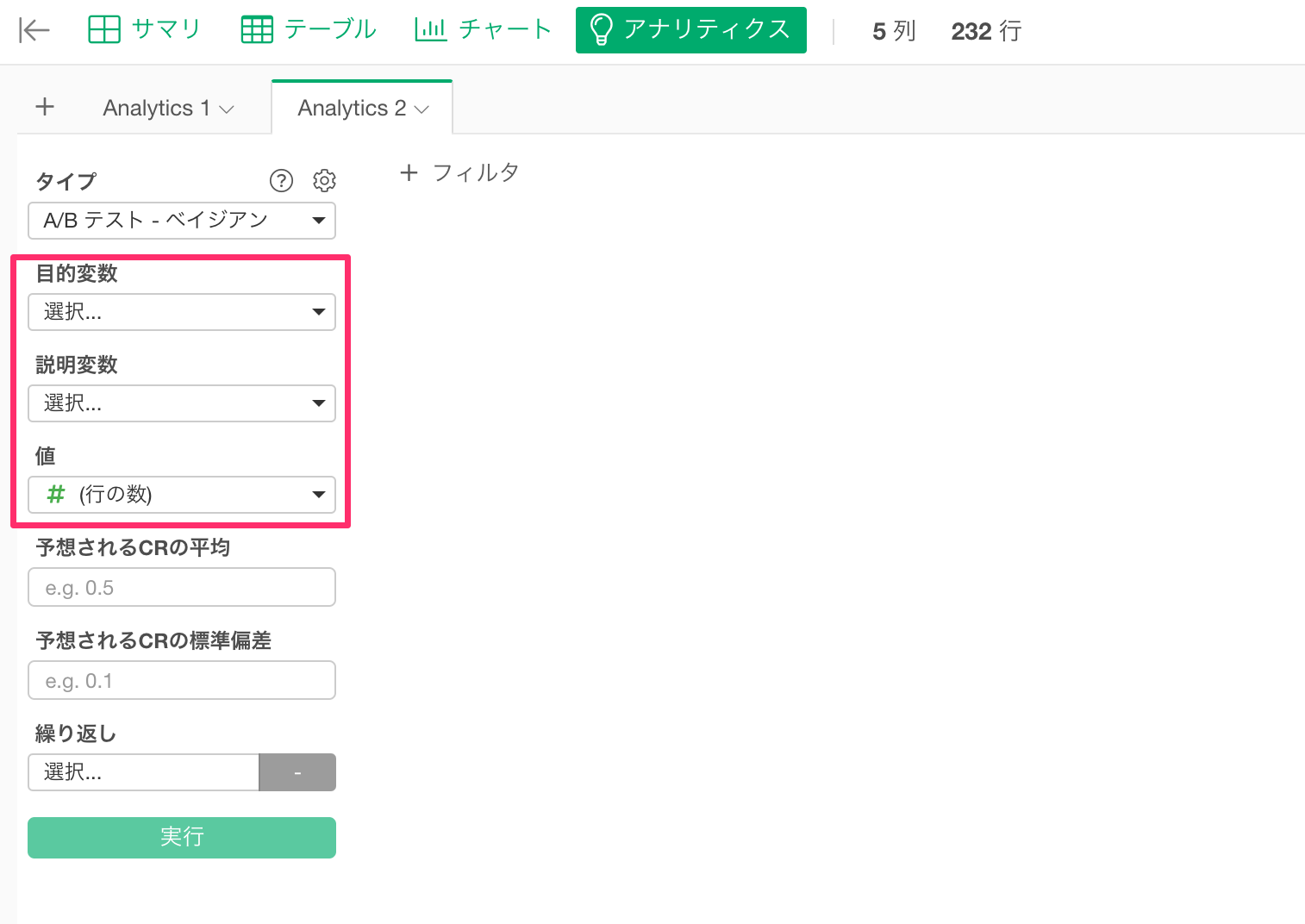
目的変数は、私たちが見たい結果の列を割り当てます。今回の場合、ユーザーがサインアップしたかどうかをみたいため、is_signupを選択します。
説明変数は、テスト対象のAとBを表す列を割り当てます。今回は、landingPagePathを選択します。
値は、AまたはBごとの各結果(サインアップかどうか)に対するサインアップ数を割り当てます。今回の場合は、valueを選択します。
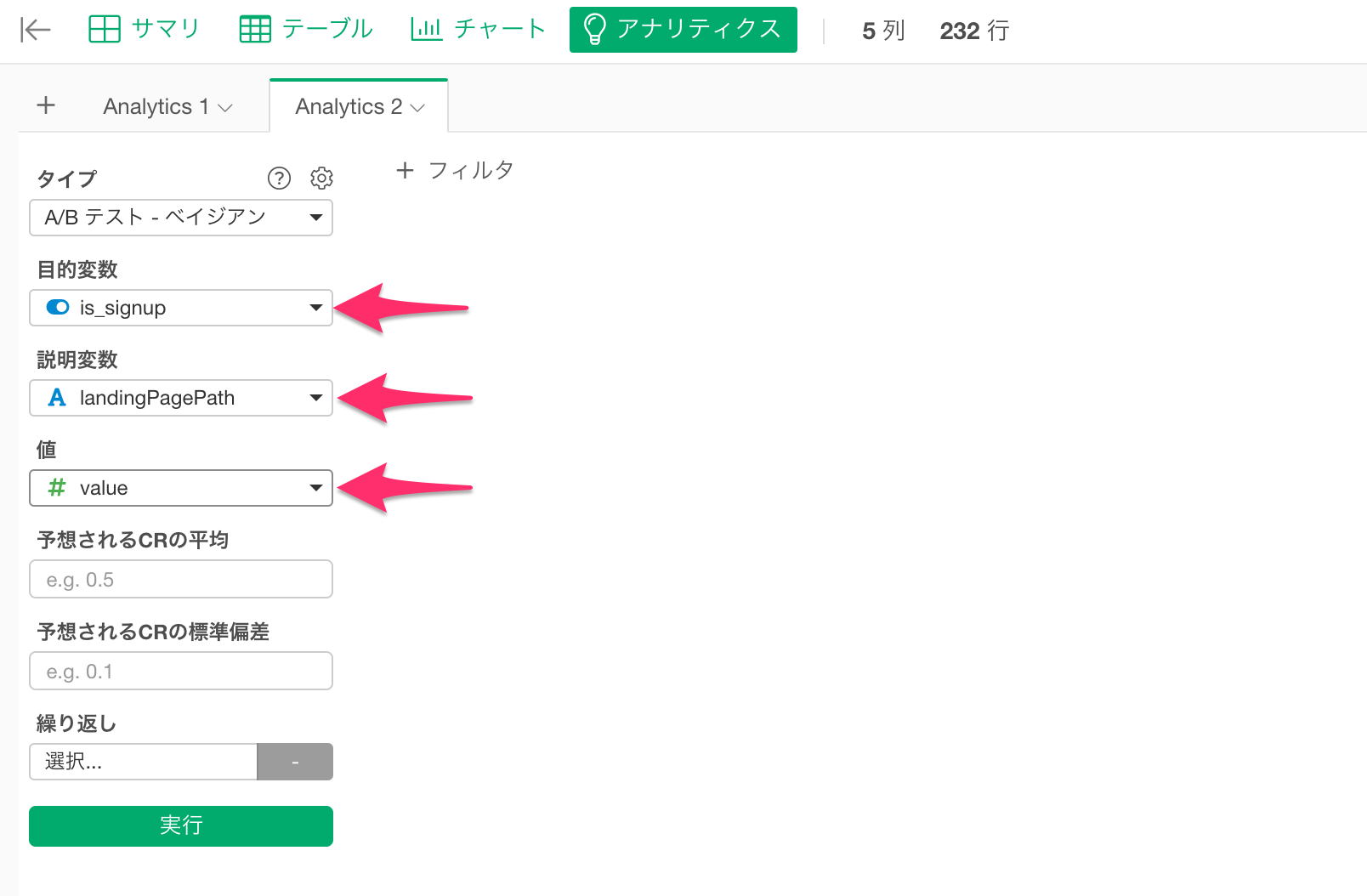
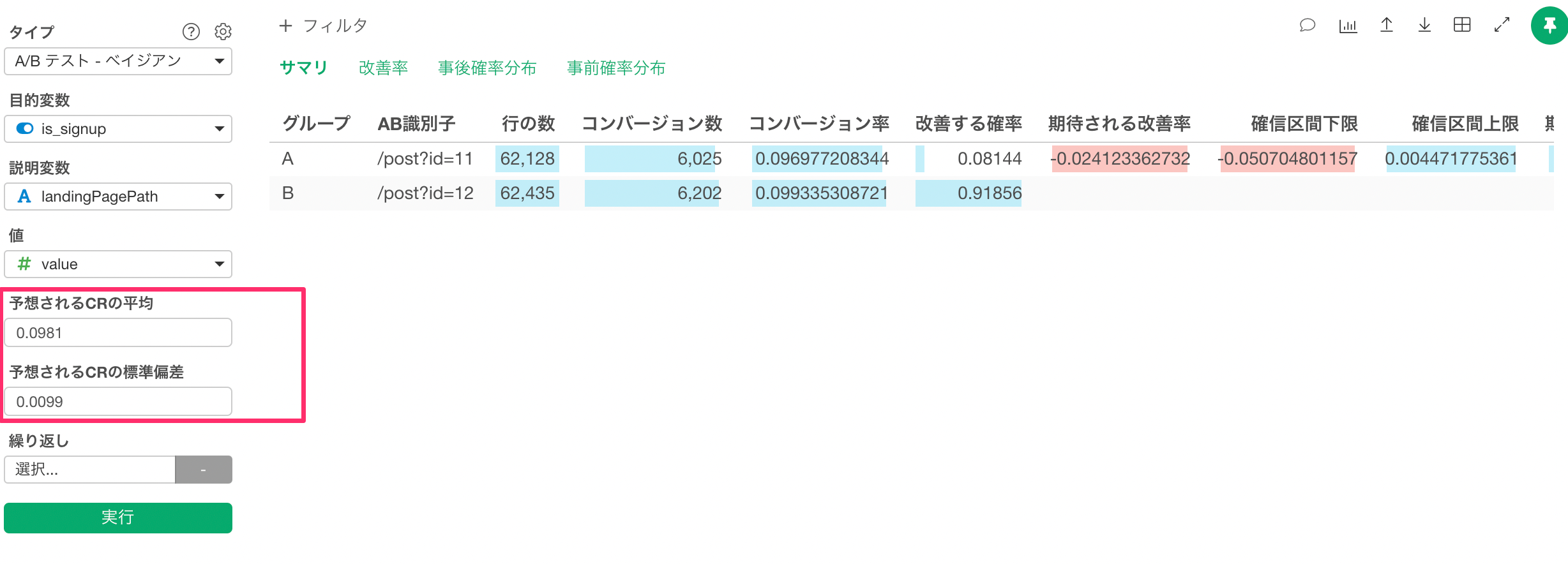
実行すると、以下のようなサマリ情報が表示されます。

このサマリ情報で最も重要な部分は、「改善する確率」の列です。この場合、Aの確率がBよりも優れているのは8%(0.08)であり、Bの確率がAよりも優れているのは92%(0.92)であることがわかります。
「期待される改善率」の列には、AがBよりどれだけ優れているかが示されています。この場合、数値は負であるため、ページAに進むと、コンバージョンが2%ほど悪化すると解釈できます。つまり、Bはパフォーマンスが2%ほど向上します。
改善率のタブに移動すると、改善する確率の確率分布を確認できます。
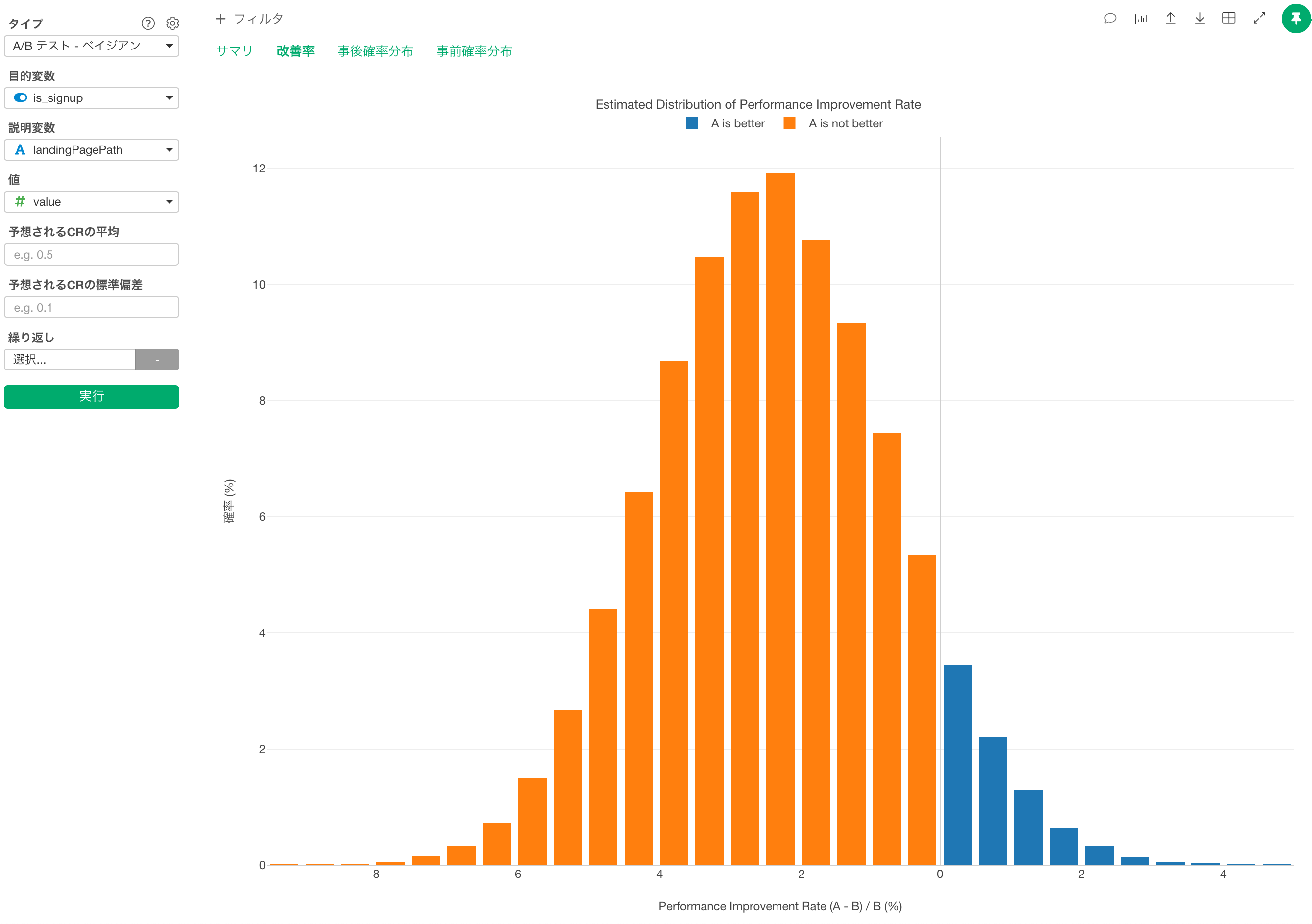
X軸は、以下のような計算で、AがBよりどれだけ優れているかを表します。
(A-B) / B * 100また、各バーはパフォーマンス改善率の確率として読み取ることができます。
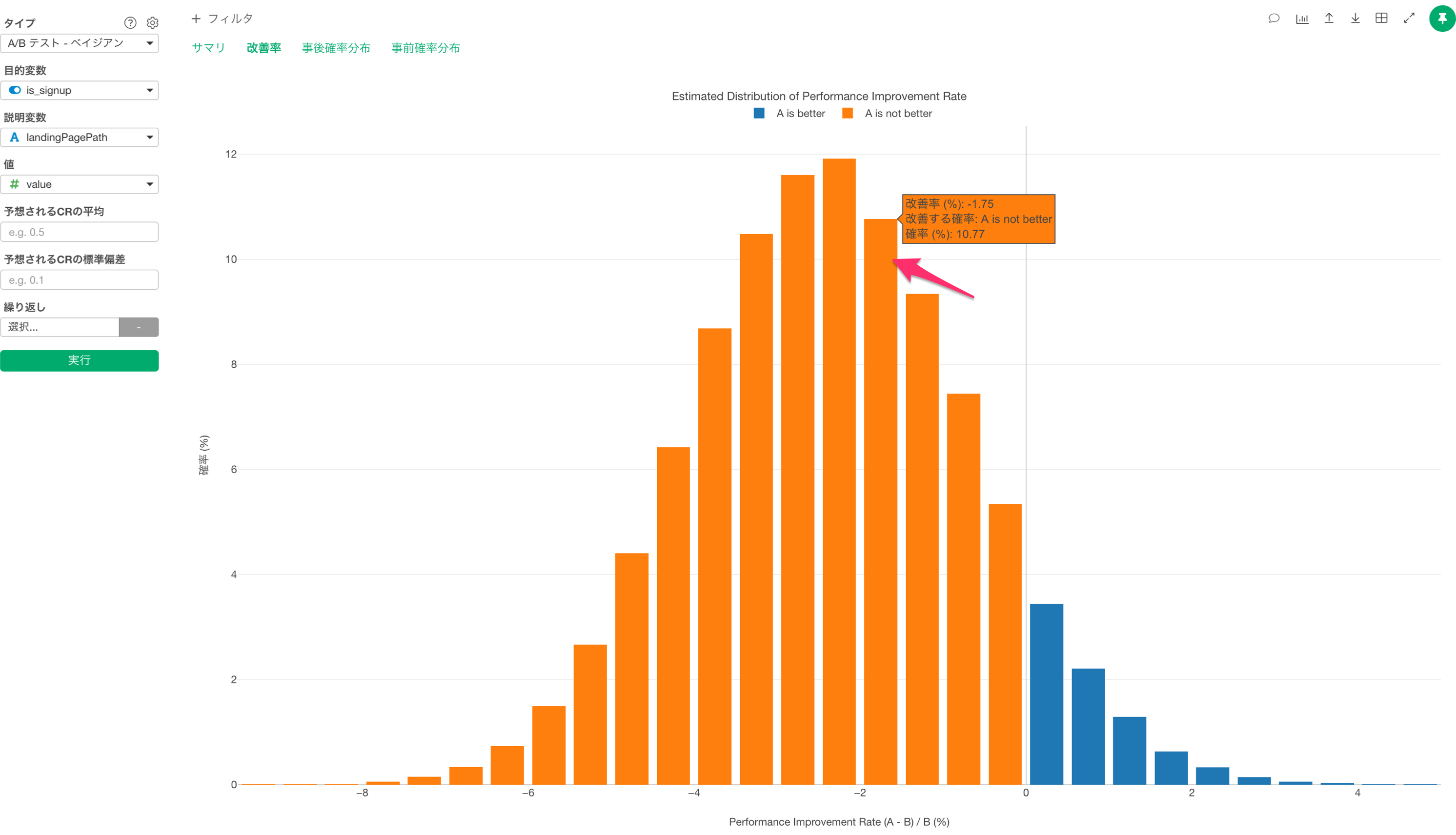
例えば、矢印が指しているオレンジ色のバーを解釈するには、「AはBより1.75%(X軸)パフォーマンスが悪く、その確率は10.9%です」と言うことができます。
そして、全てに対するオレンジ色の領域全体の比率(およびすべてに対する青色の比率)は、サマリタブの「改善する確率」の列の下に表示される数値です。
事前情報の追加
上記評価は、事前情報を明示的に設定せずに行いました。事前情報を追加しない場合は、分布に関する事前知識がないと想定し、一様分布を事前情報として使用します。これは十分なデータサイズがあれば問題ありません。しかし、最初の数日間しかデータがない場合は、そうではない可能性があります。
事前情報を提供するには、過去のコンバージョン率の平均と標準偏差を提供して、Exploratoryが事前情報を内部で計算できるようにします。

平均と標準偏差(SD)を取得する方法は?
過去のデータをインポートすることで、コンバージョン率の平均と標準偏差をExploratoryで簡単に計算することができます。
下記が過去のユーザーのコンバージョンのデータであるとします。(先ほど使用したデータと同じものを使用しています。)
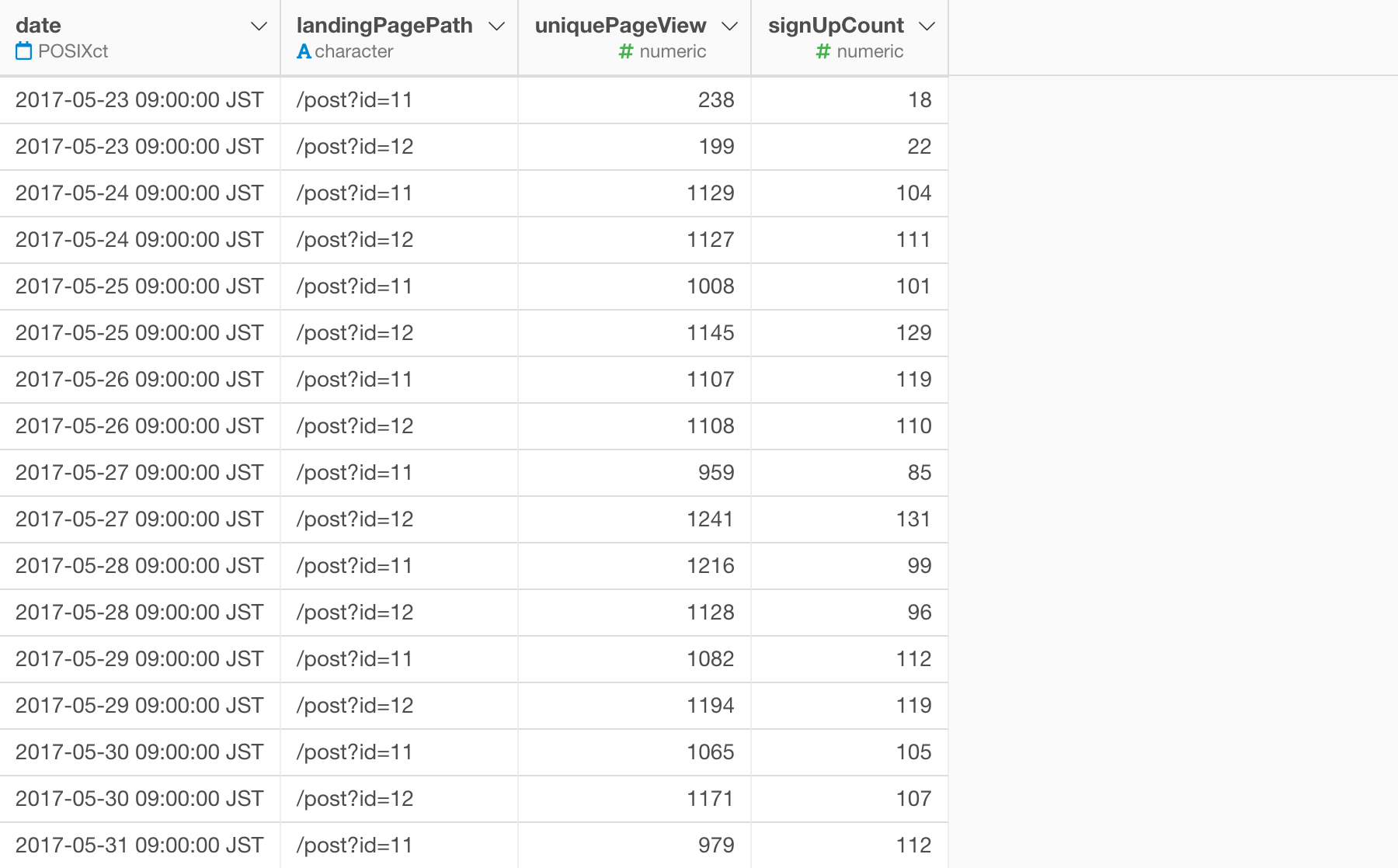
最初にコンバージョン率を計算する必要があります。
列ヘッダーメニューから「計算の作成」を選択します。
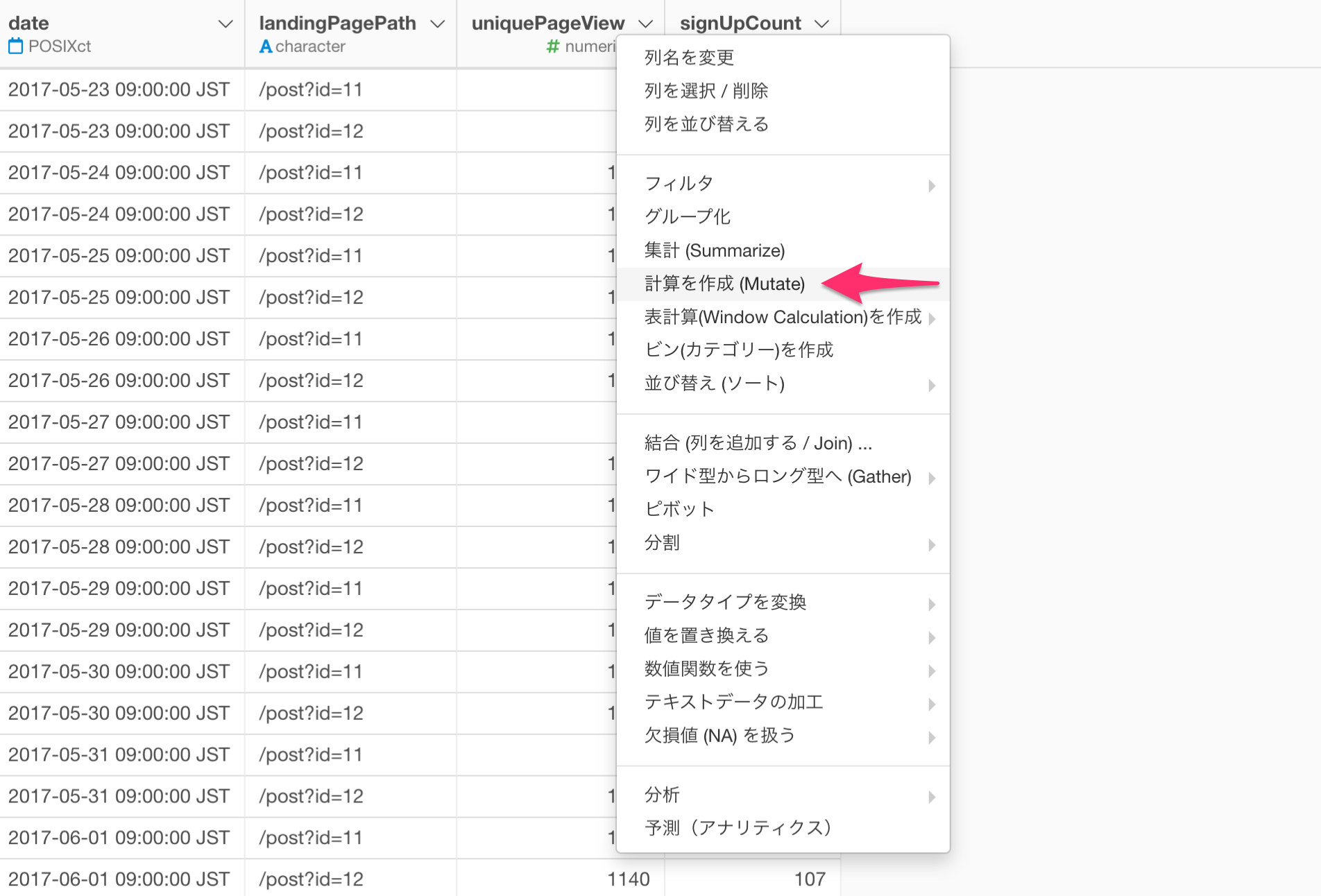
以下のように入力してコンバージョン率を計算します。
signUpCount / uniquePageView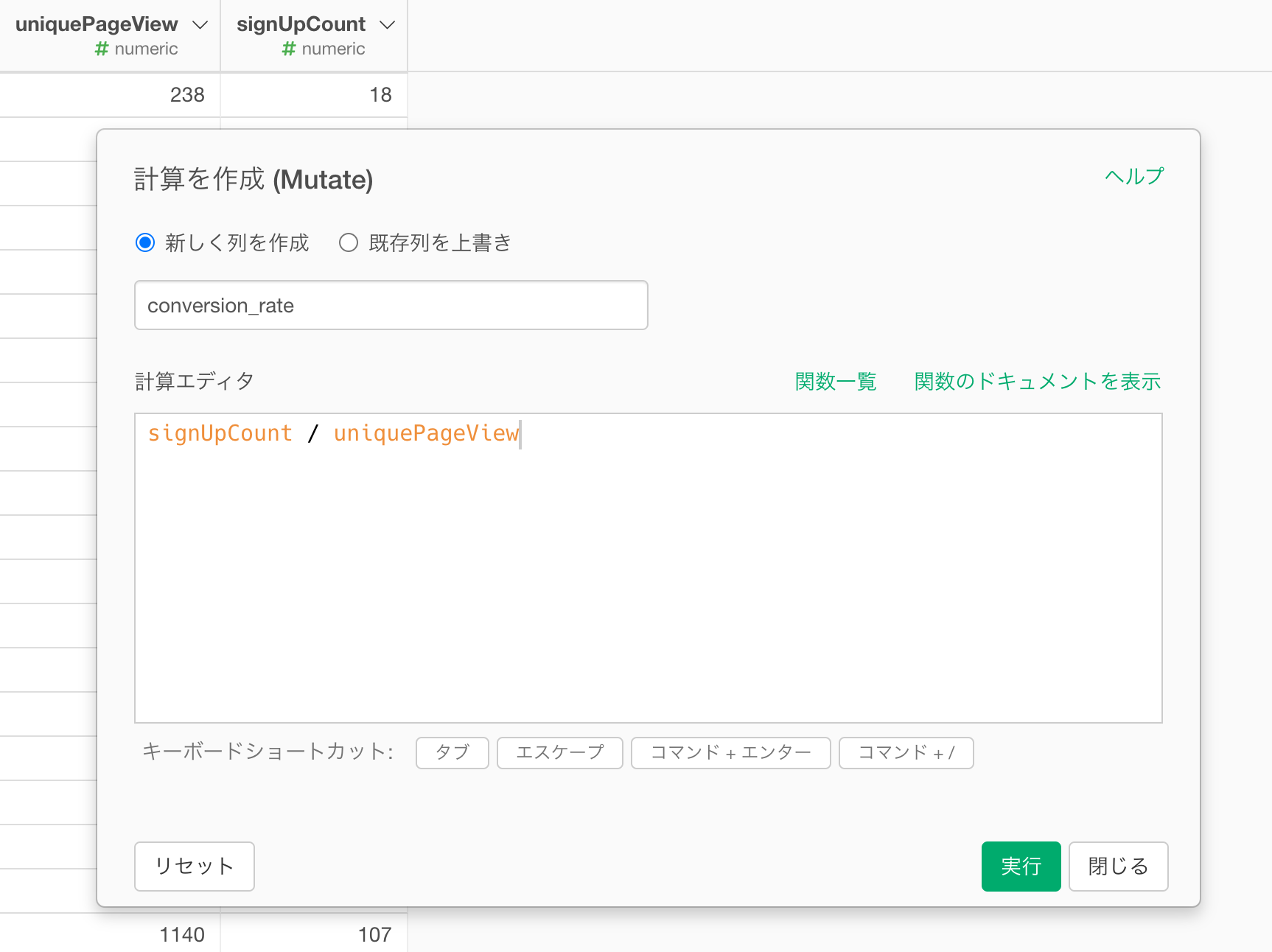
これが、日毎の各ページのコンバージョン率です。
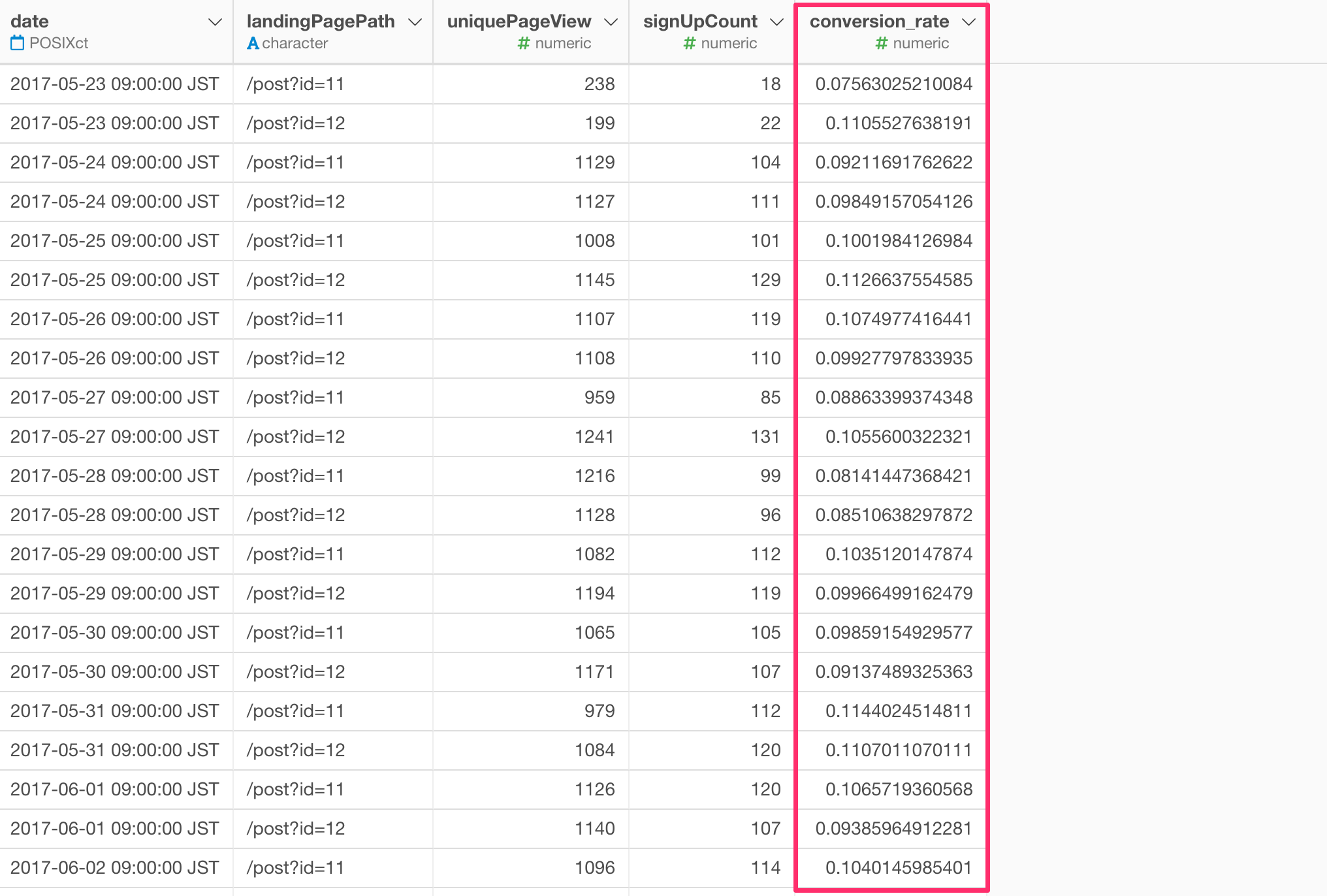
この列を作成したら、サマリビューに移動して、コンバージョン率の平均値と標準偏差を確認できます。
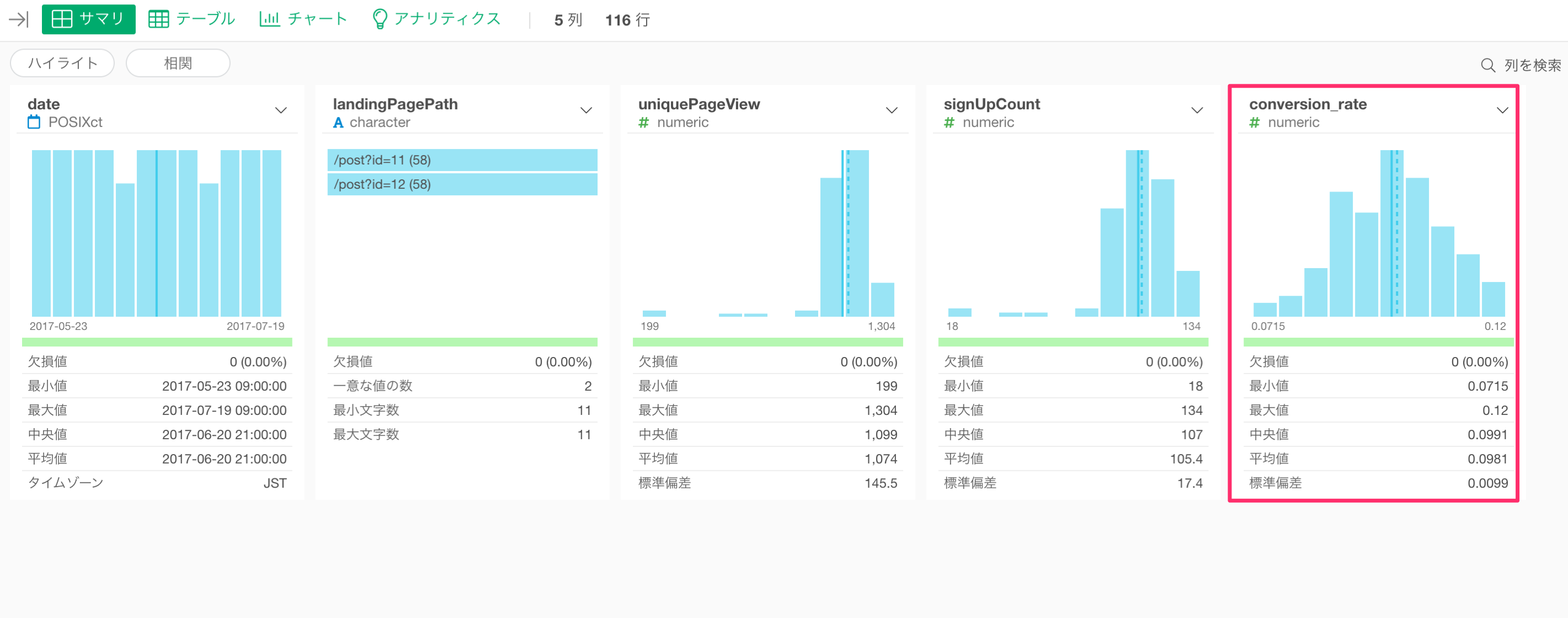
コンバージョン率の平均値は0.09(9.8%)、標準偏差は0.009(0.9%)であることがわかります。次に、これらの数値をベイジアンA/Bテストに指定します。
以上です!
上記で述べたように、A/Bテストの結果を評価する方法はいくつかあります。どちらを選択するかは、ニーズによって異なります。一方が他方より優れているわけではありません。
ただし、結果をリアルタイムでモニタリングおよび評価し、統計を知らない人と結果を伝達する必要がある場合は、ベイジアンA/Bテストを試してみてください。