給料が異常に高いまたは低い（外れ値）従業員にラベルをつける方法

給料が以上に高いまたは低い（外れ値）従業員にビンを使ってラベルを付ける方法を紹介します。また、外れ値検知の違いについても説明します。

今回はサンプルデータとして従業員データを使用します。

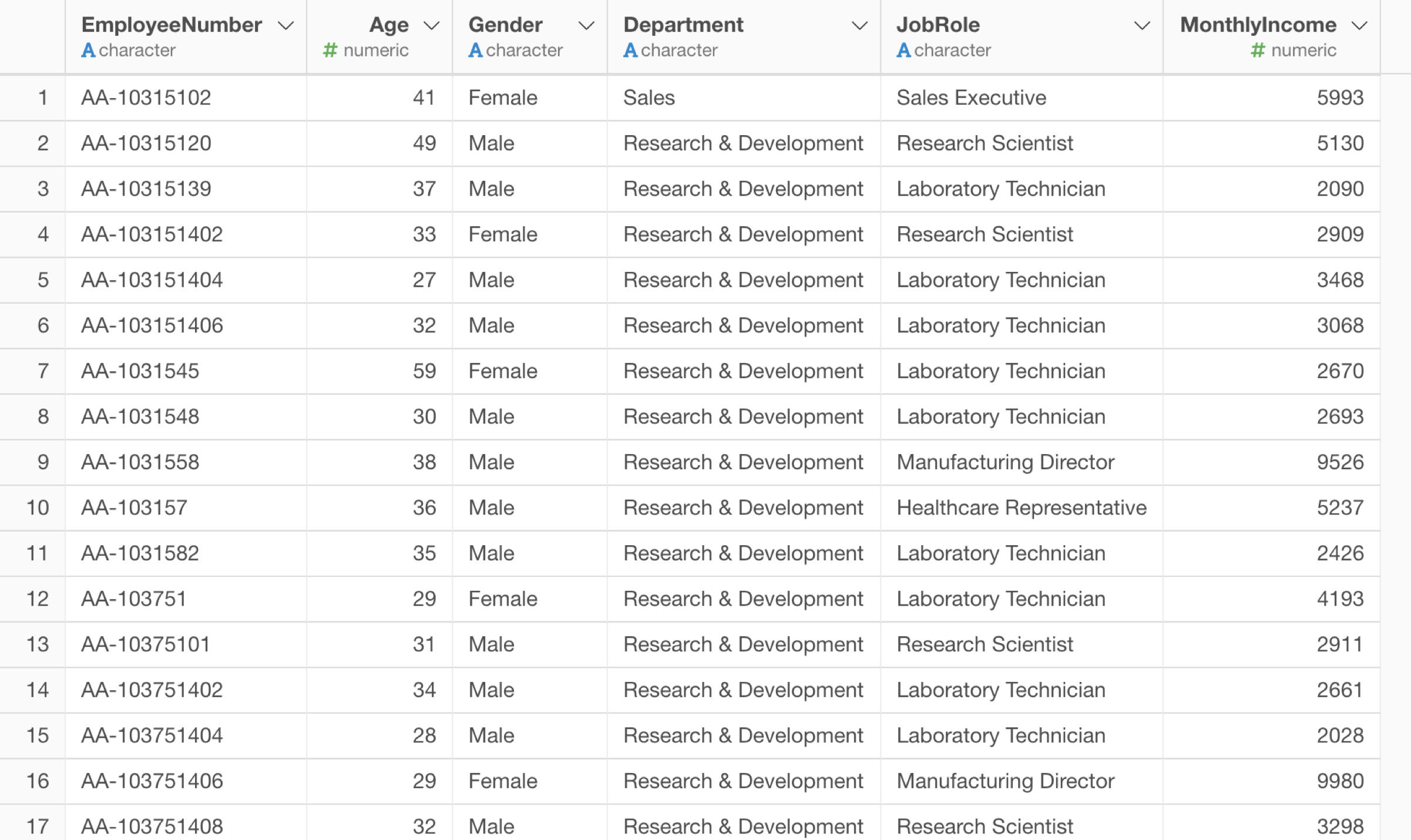
例えば、ヒストグラムで給料の分布を可視化します。

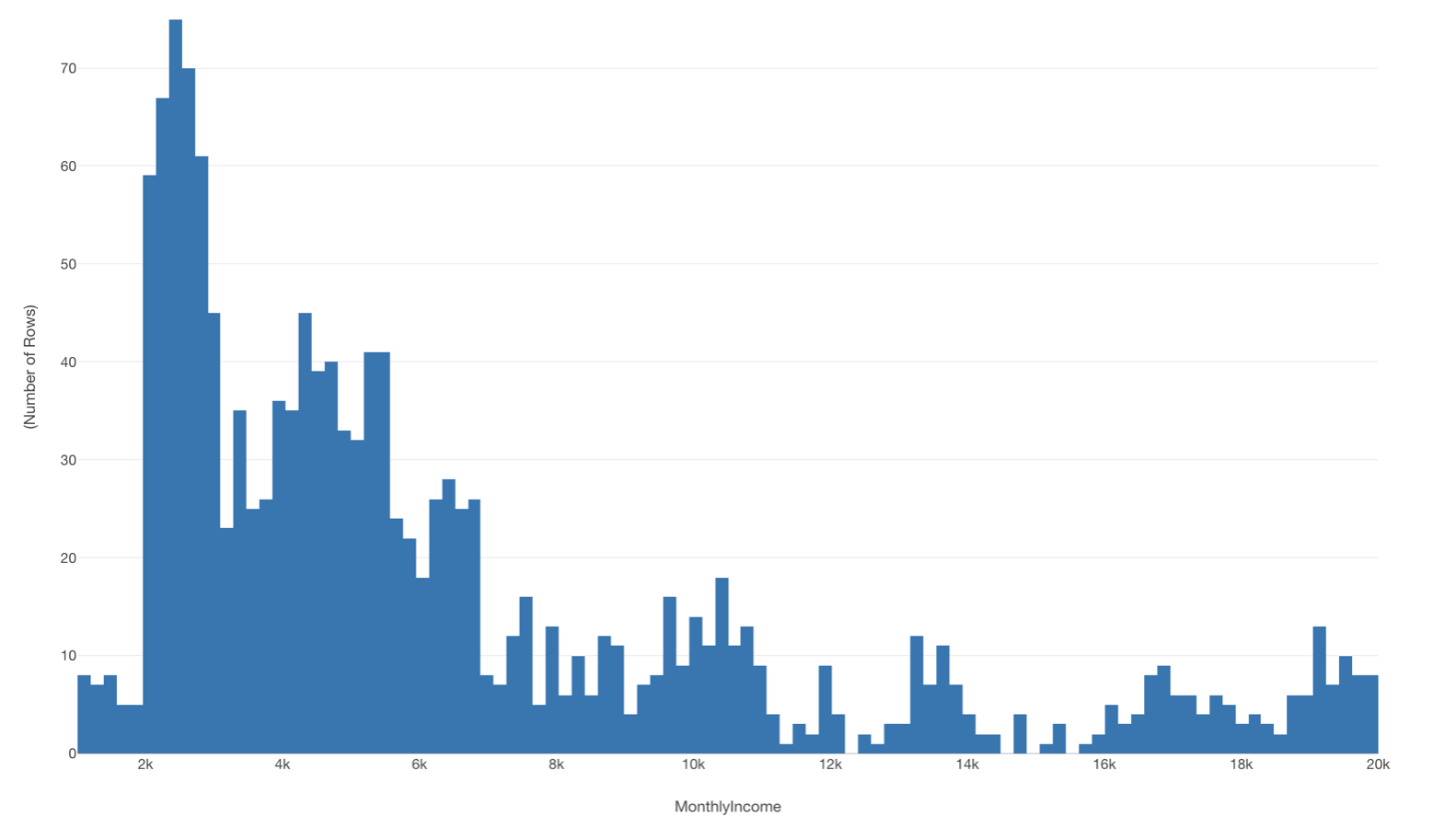
いったいどの人が給料が異常に高いのかもしくは低いのか（外れ値）がわかりません。

そのため、給料が外れ値である従業員にラベルをつけたいです。

その前に、外れ値があるとなぜ問題なのでしょうか？

外れ値の問題点

外れ値の問題点としては主に、

1. データ全体としての性質が、少数の外れ値によって歪められてしまうことがある。
2. 平均値が外れ値によって引っ張られることにより、データの推測が正確に行えなくなる。

と言ったことが挙げられます。

外れ値検知のタイプ

Exploratoryでは、外れ値検知のタイプは下記の3つの種類があります。

1. 標準偏差
2. パーセンタイル
3. 四分位範囲 (IQR)

それぞれの違いについて説明します。

標準偏差

まず初めに、標準偏差を使って外れ値を探す方法を説明します。

もし、分布が正規分布であれば値のうち95% は平均から2標準偏差以内に入ると言われています。

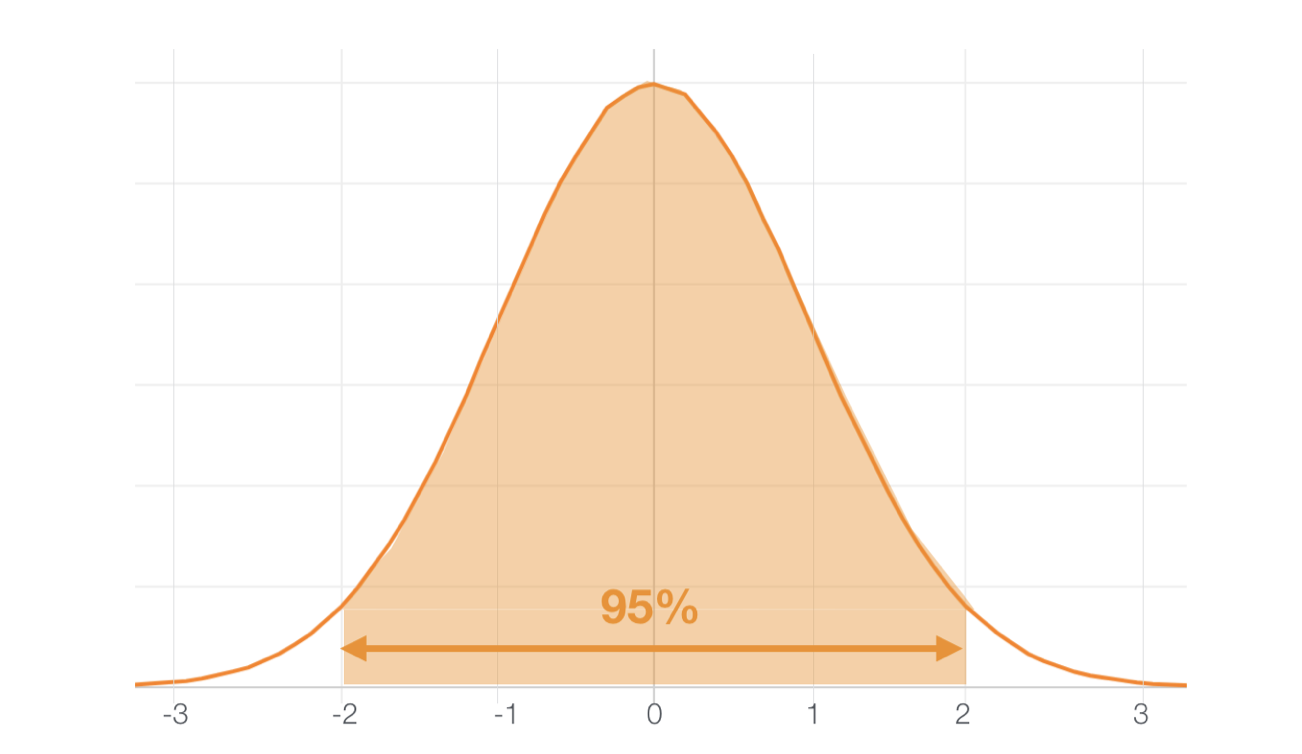
標準偏差で外れ値を探す方法では、標準偏差の範囲外の値を外れ値として扱います。

1標準偏差の範囲外を外れ値として扱う場合

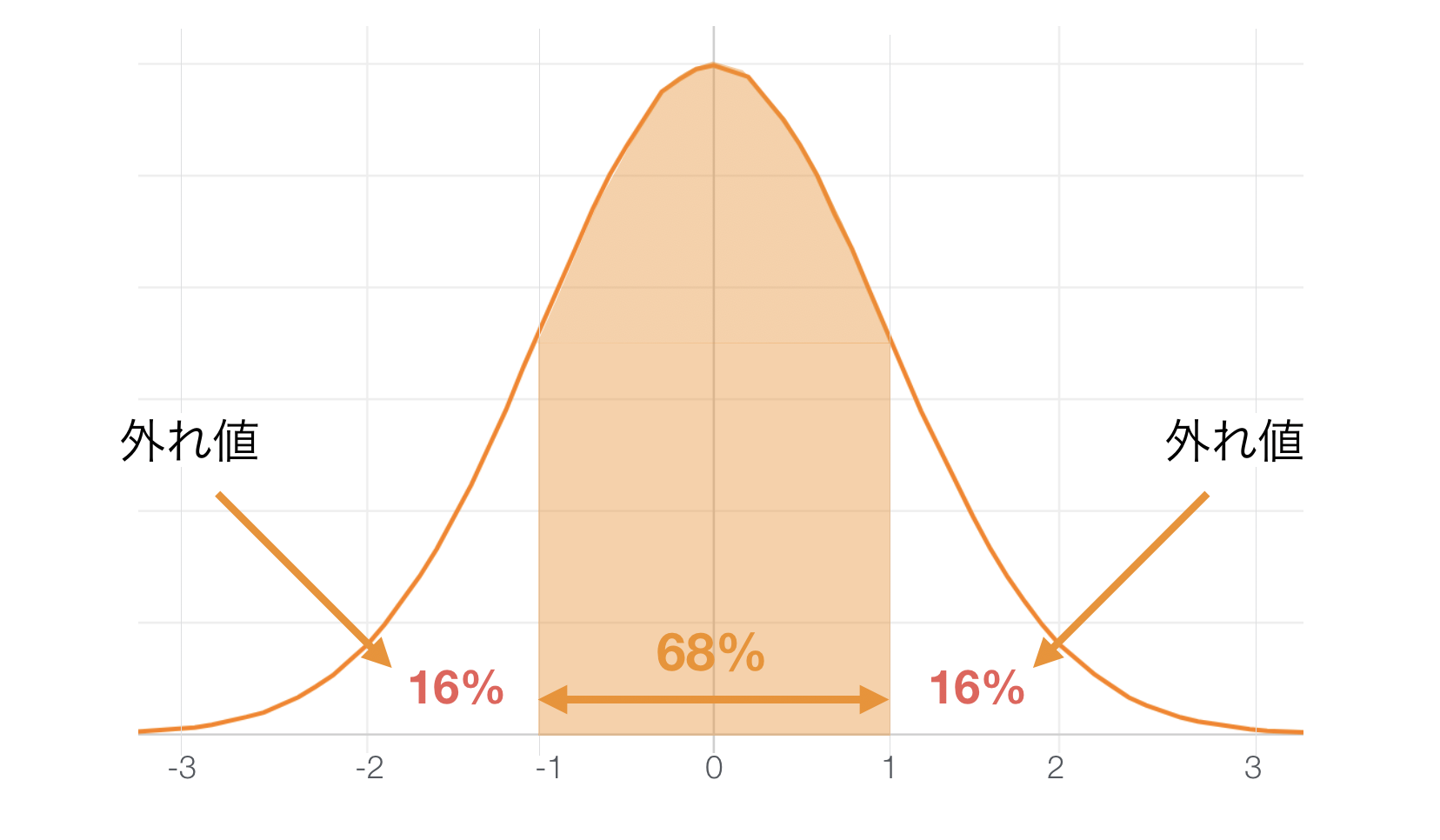
正規分布であれば1標準偏差の範囲内に 68% の値が入ると言われています。そのため、範囲外の32%を左片側で16%、右片側で16%のように分けてその範囲に位置する値を外れ値として扱います。

2標準偏差の範囲外を外れ値として扱う場合

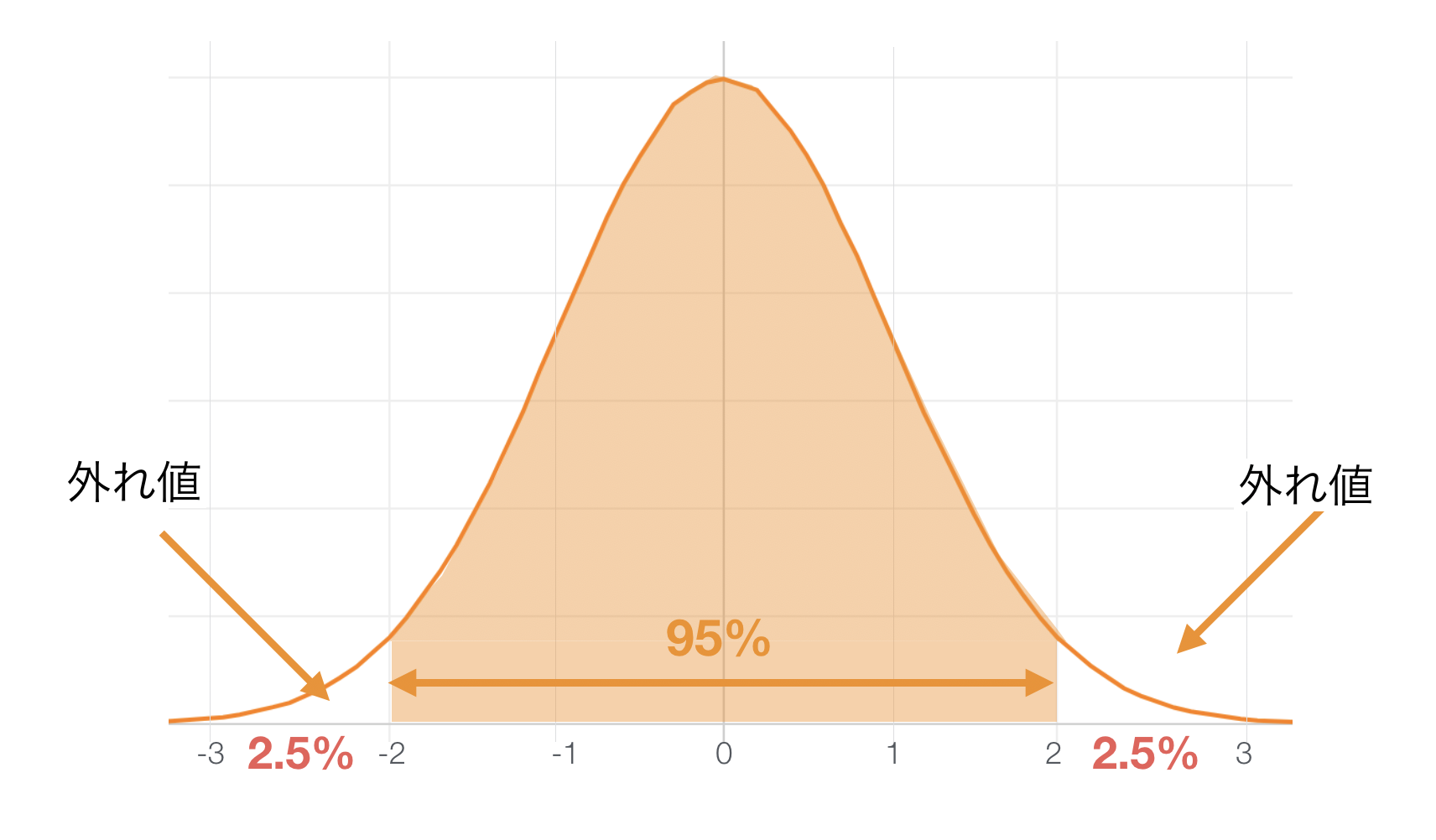
次に、正規分布であれば2標準偏差の範囲内に 95% の値が入ると言われています。そのため、範囲外の5%を左片側で2.5%、右片側で2.5%のように分けてその範囲に位置する値を外れ値として扱います。

3標準偏差の範囲外を外れ値として扱う場合

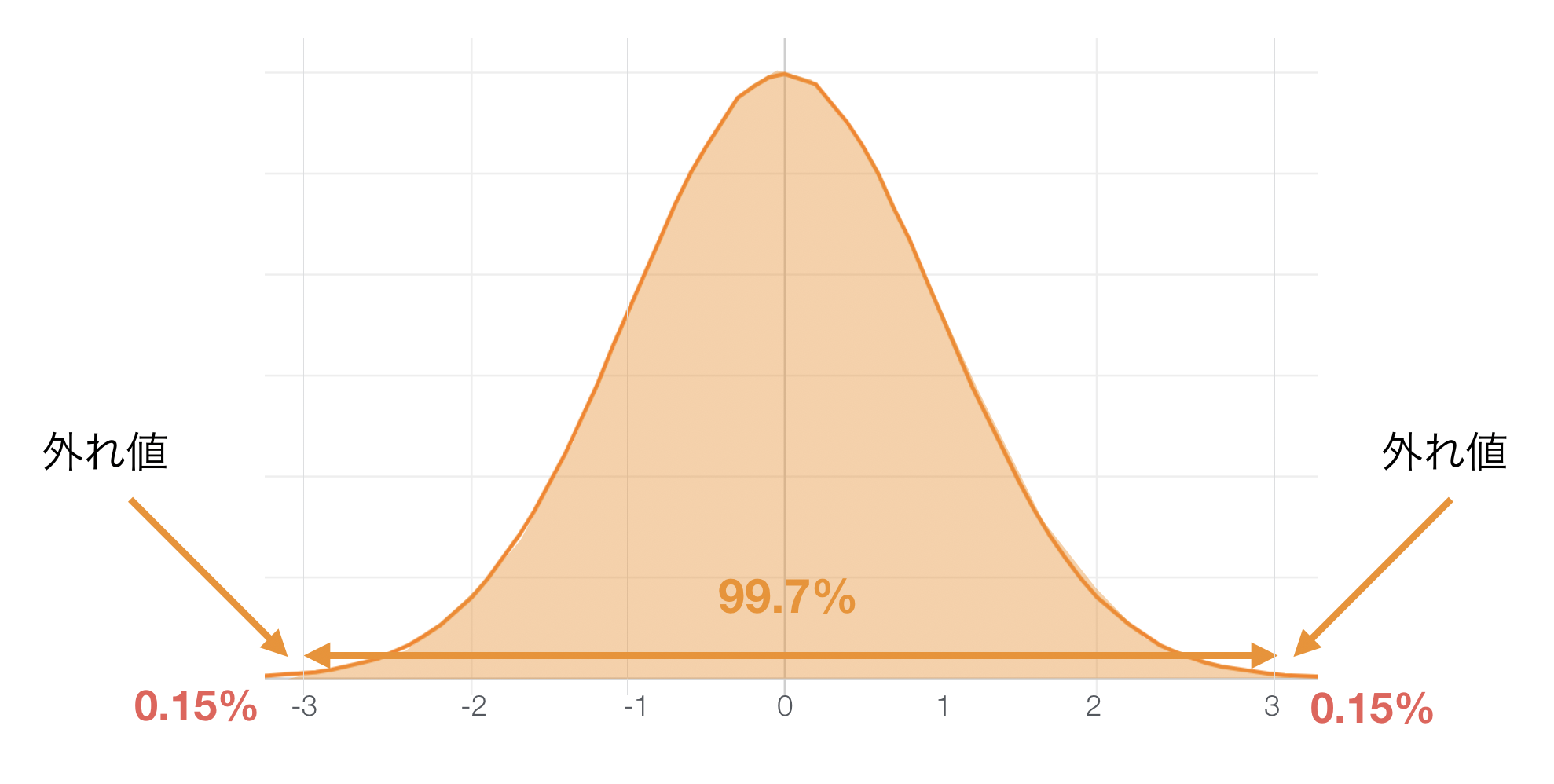
正規分布であれば3標準偏差の範囲内に 99.7% の値が入ると言われています。分布の裾の部分にはわずかながらも0.3%の値があり、左片側で0.15%、右片側で0.15%の範囲内に位置する値を外れ値として扱います。

チェビシェフの不等式

もし分布が正規分布じゃなかったとしても、安心してください！

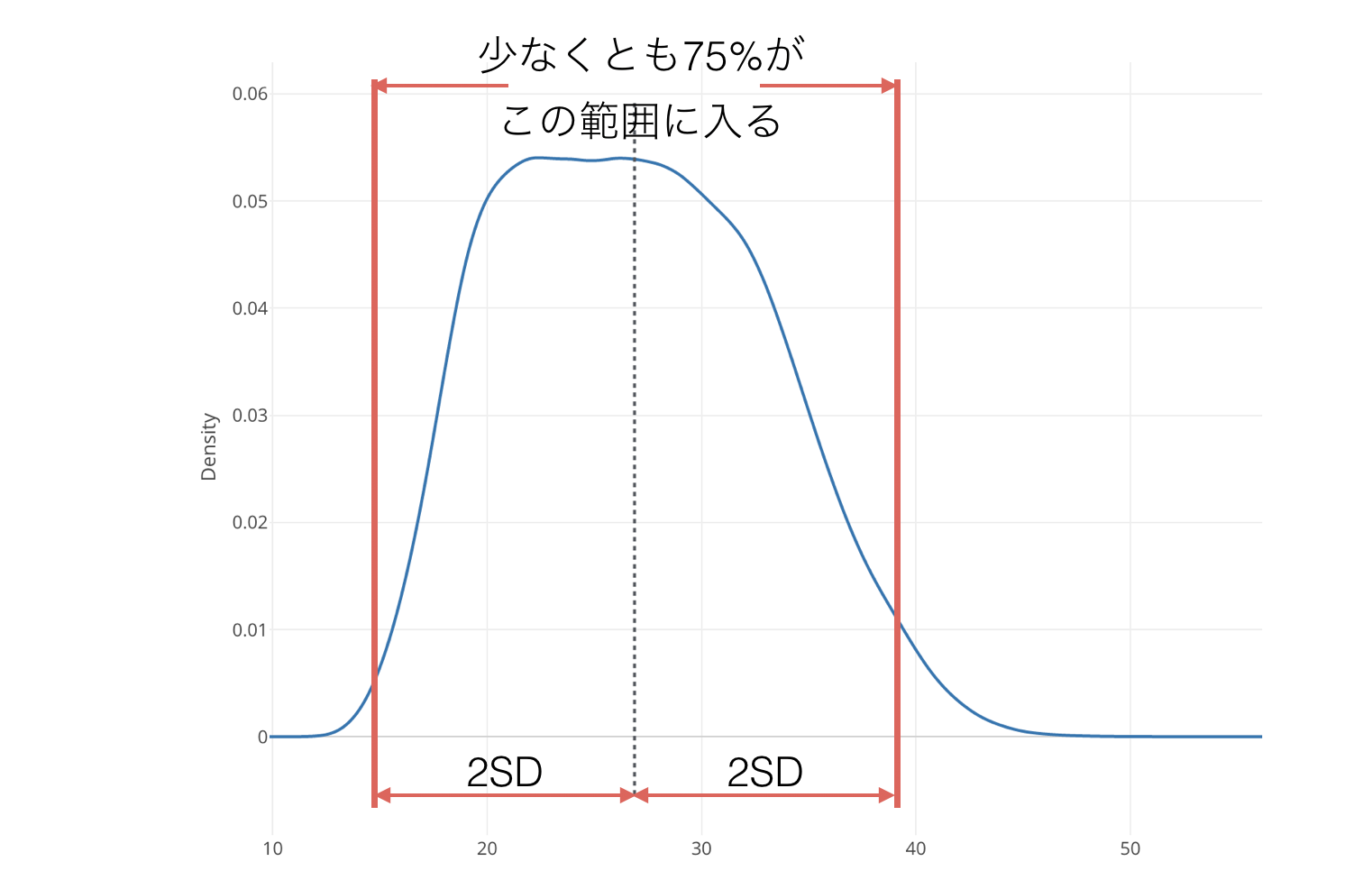
チェビシェフの不等式と言って、どのような分布だとしても平均から2標準偏差の範囲内に少なくとも75% の値が入ると言われています。

2標準偏差を使って外れ値を探す

給料の列を元に、2標準偏差を使って外れ値のラベルを作りヒストグラムの色に割り当てます。

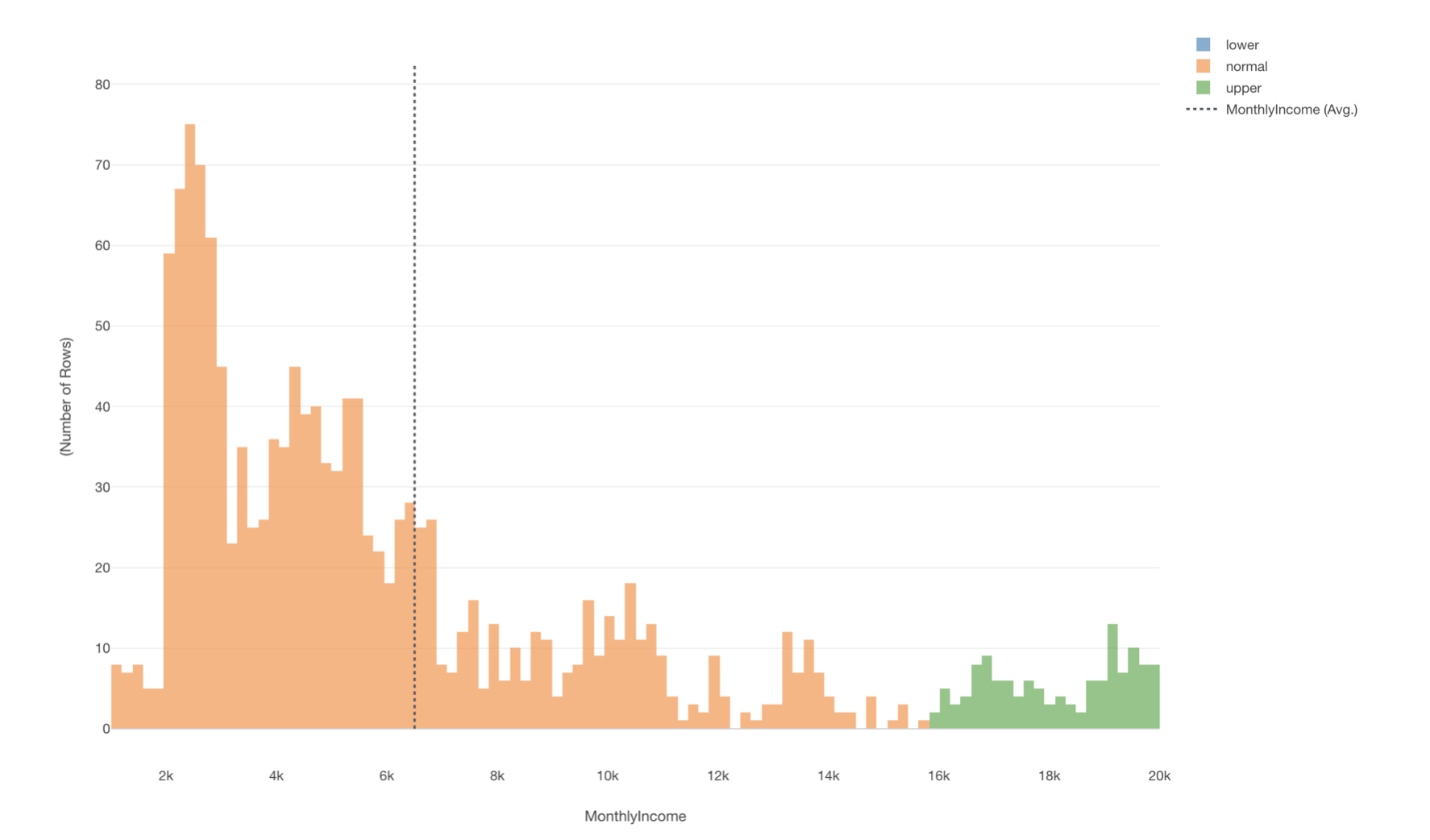
今回のデータでは、給料が異常に低い従業員はいませんでしたが、給料が異常に高い人たちは何人かいることがわかります。

サマリ・ビューで確認してみると、給料が異常に高い人たちは128人いることがわかりました。

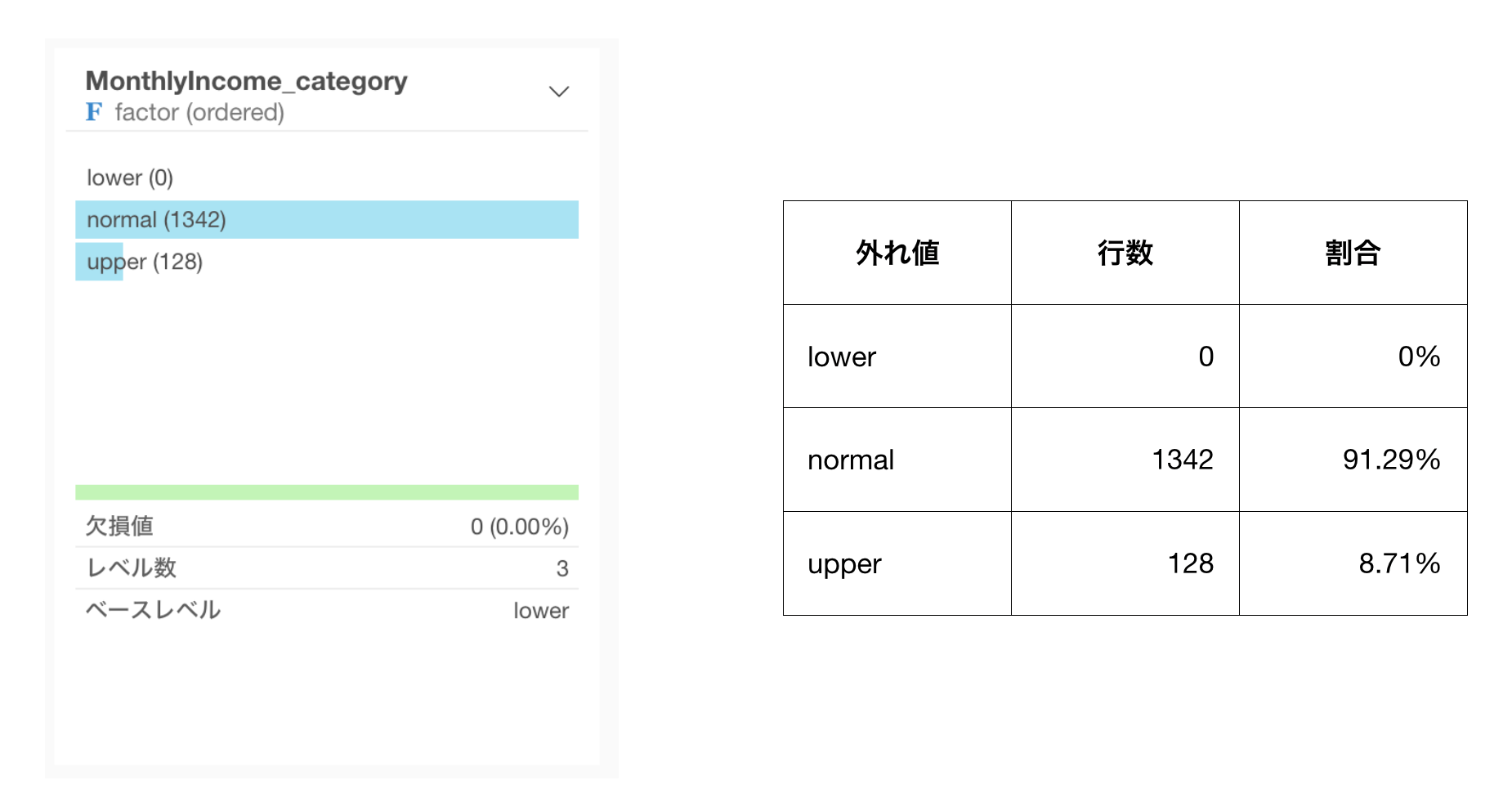
外れ値じゃない人たちは全体の約91.3%ということがわかり、正規分布でなくても2標準偏差の中に75%以上の値が入ると言われているチェビシェフの不等式が当てはまっていることが確認できます。

パーセンタイル

次に、パーセンタイルを使って外れ値を探す方法を説明します。

パーセンタイルは値自体を無視して、順位に着目する方法です。

具体的には、データを大きさ順に並べて、その値いかが全体の何パーセントを閉めるかでその値のパーセンタイルが決まります。

下記の画像の赤い色でつけられた人に注目します。

この人は小さい方から10人中9番目に位置するので、90パーセンタイルとなります。

90パーセンタイルを使って外れ値を探す

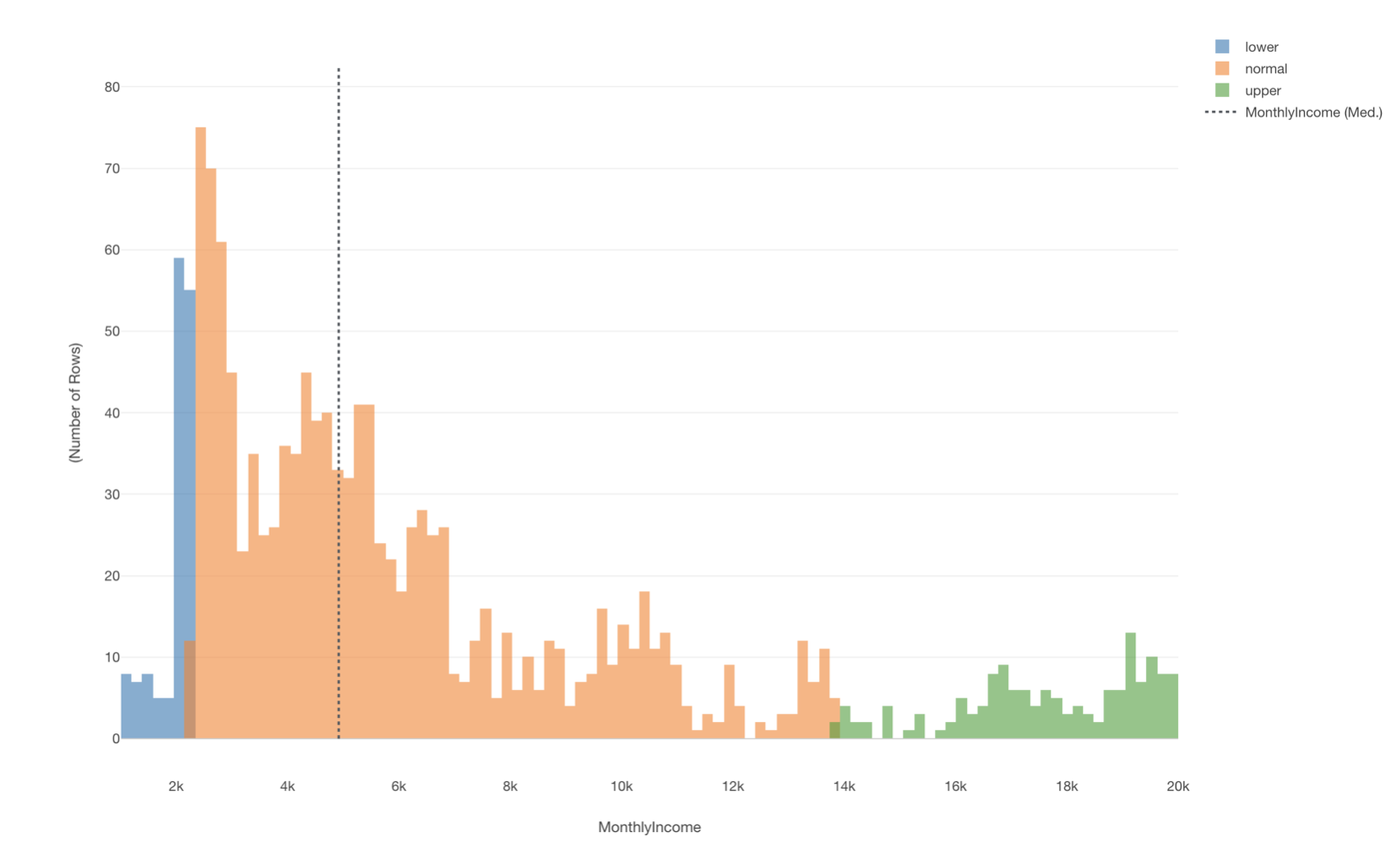
こちらも給料の列を元に、90パーセンタイルを使って外れ値のラベルを作りヒストグラムの色に割り当てます。

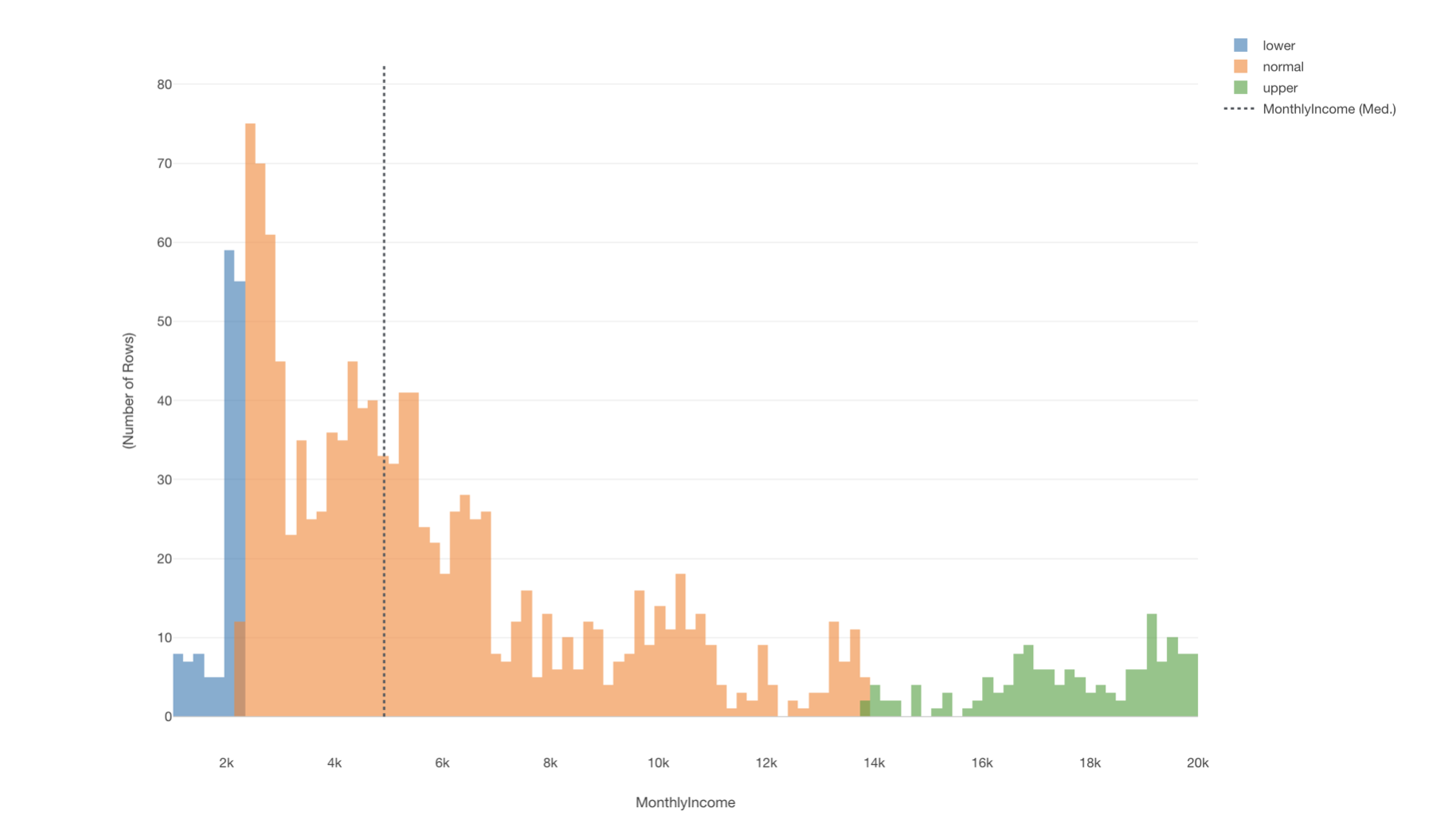
パーセンタイルでは、給料が低い従業員と高い従業員の数を等しく外れ値としてラベルをつけることができます。

サマリ・ビューで確認してみると、給料が異常に高い人と低い人は等しく147人いることがわかりました。

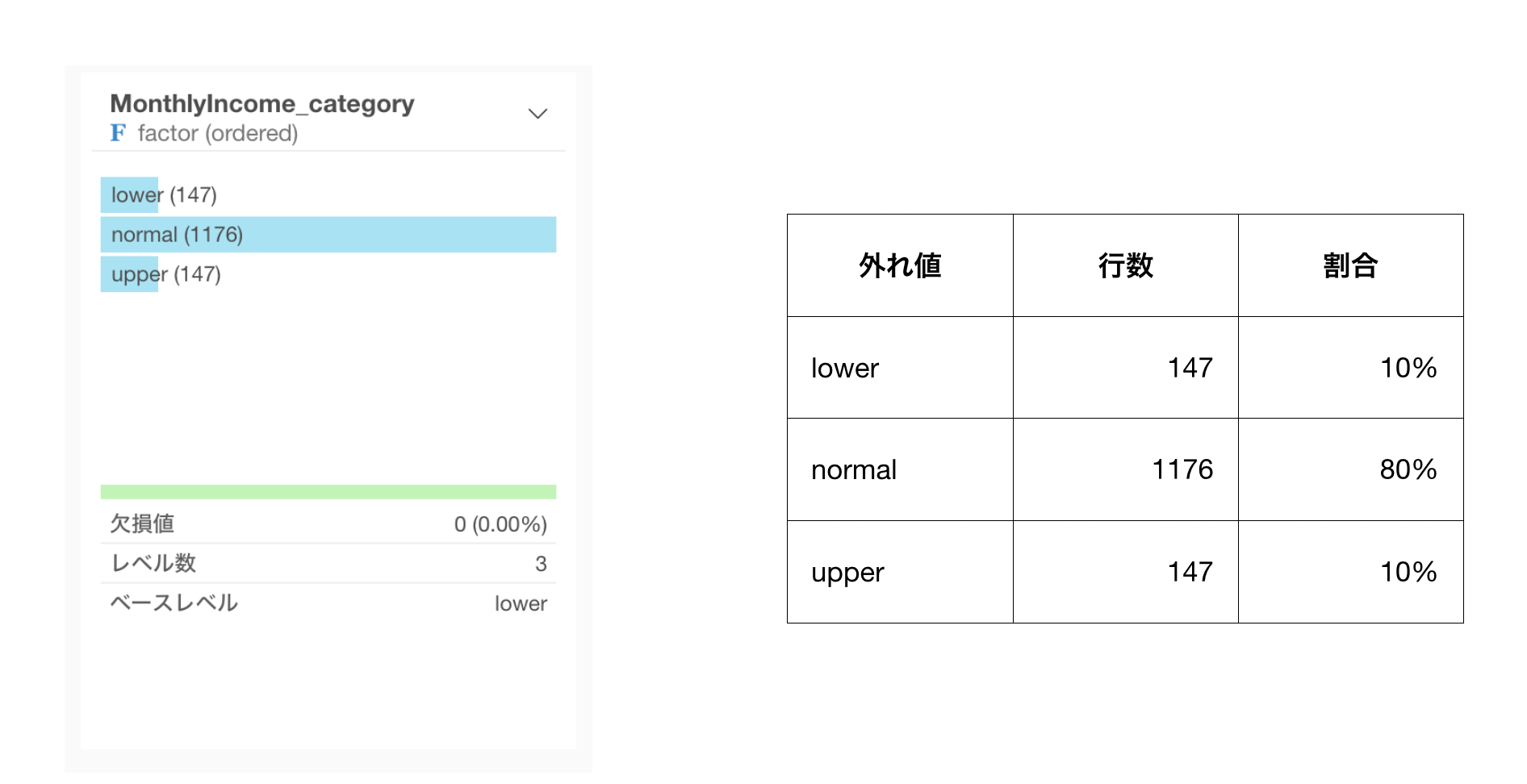
そして、どちらも割合は10%となっていることが確認できます。

四分位範囲 (IQR)

最後に、四分位範囲 (IQR)を使って外れ値を探す方法を説明します。

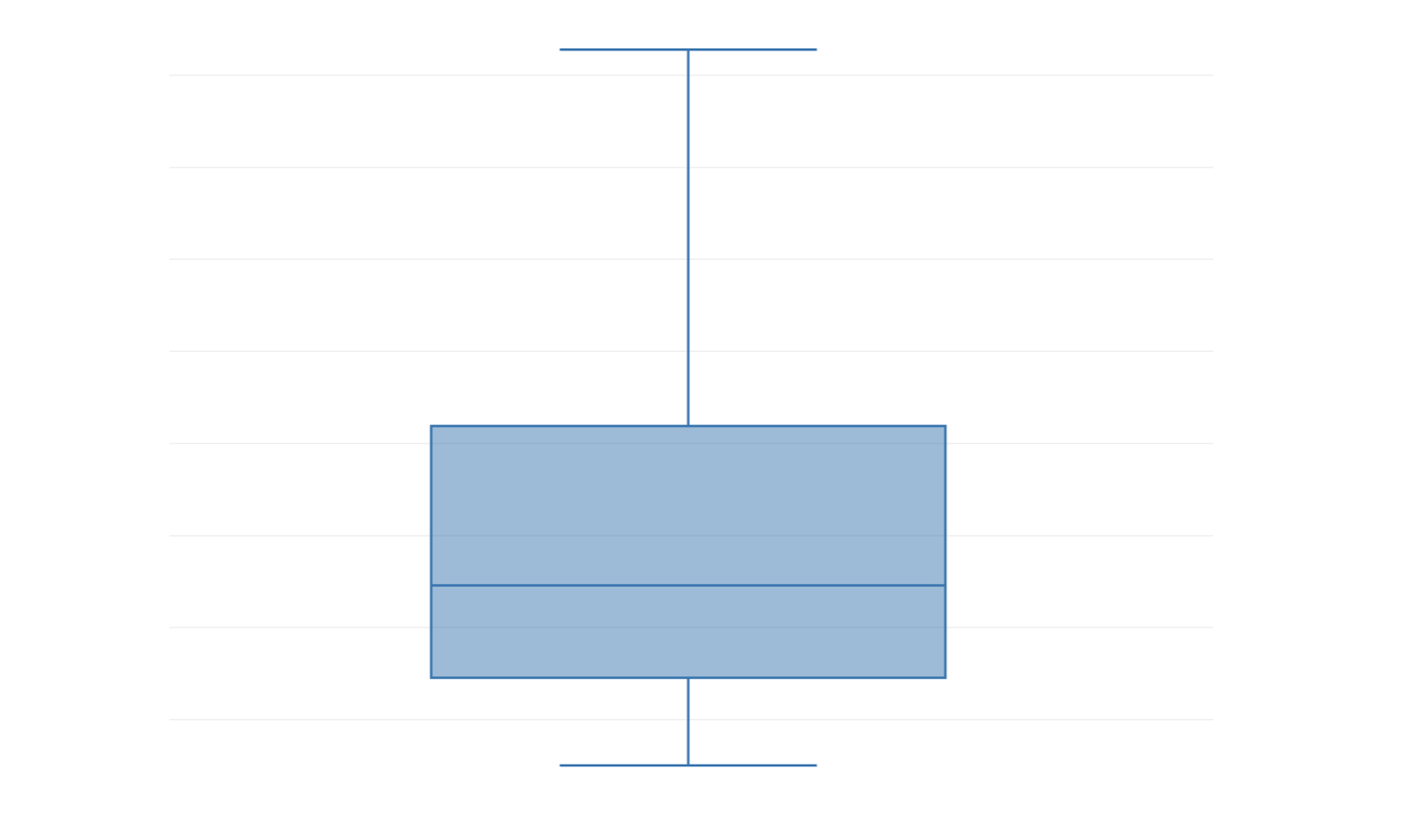
四分位範囲の説明の際、箱ヒゲ図を使って説明することが多いので、まずは箱ヒゲ図について説明します。

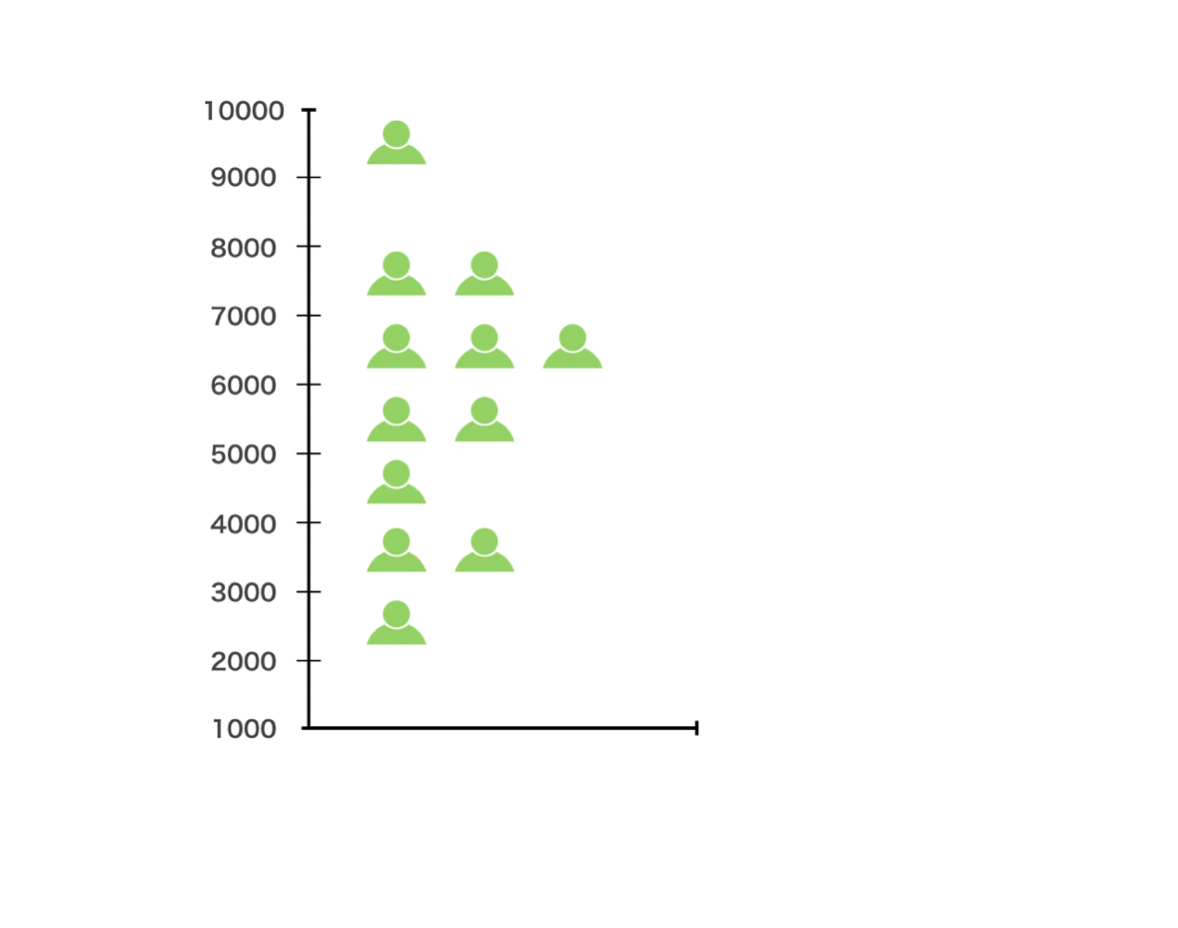
例えば、ヒストグラムを縦向きにしてみます。

次に、それぞれのサイズ（行の数）が等しくなるように4つのグループに分けます。

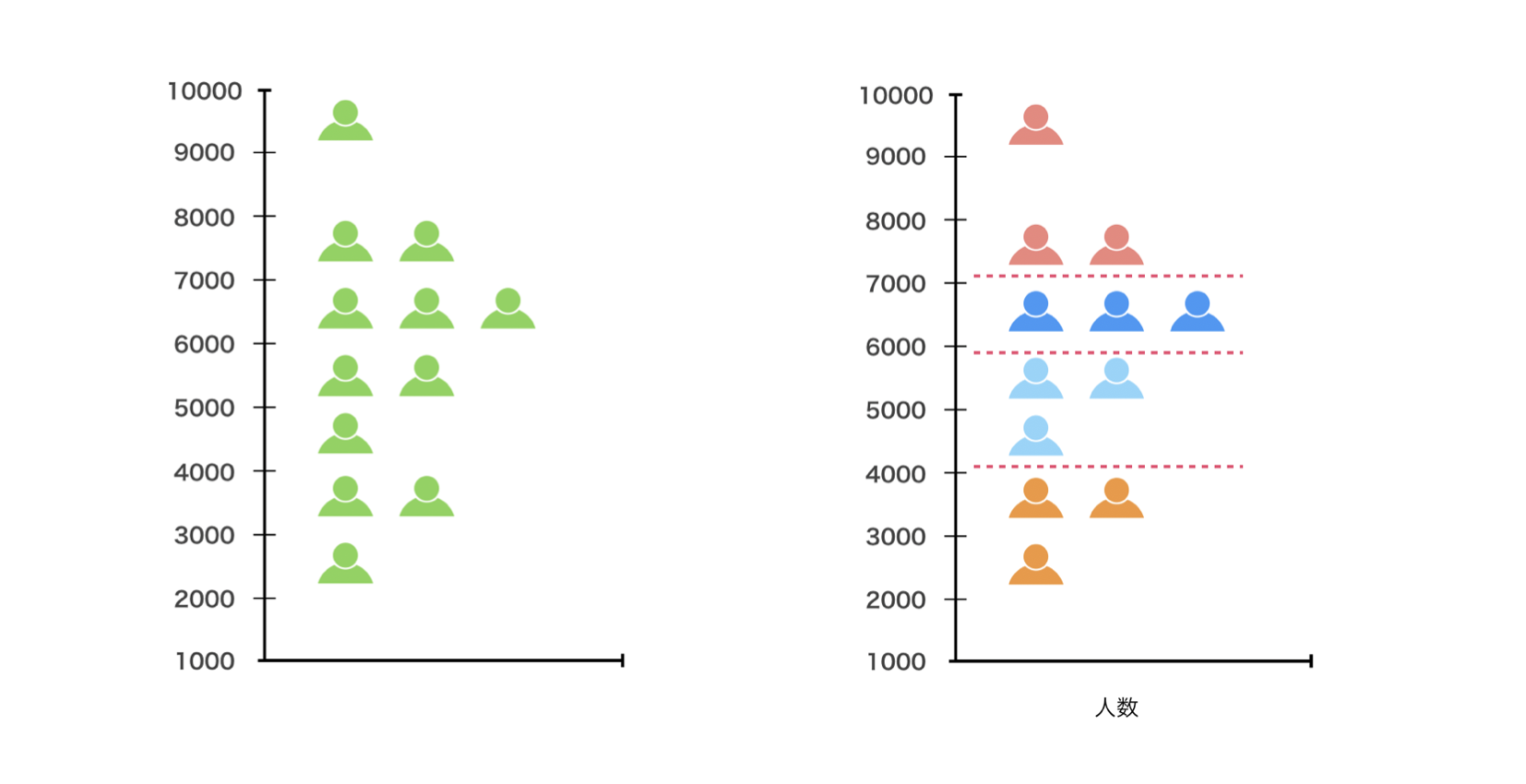
そして、25パーセンタイル地点を1Q(第1四分位)、50パーセンタイル地点を中央値、75パーセンタイル地点を3Q(第3四分位)と呼びます。

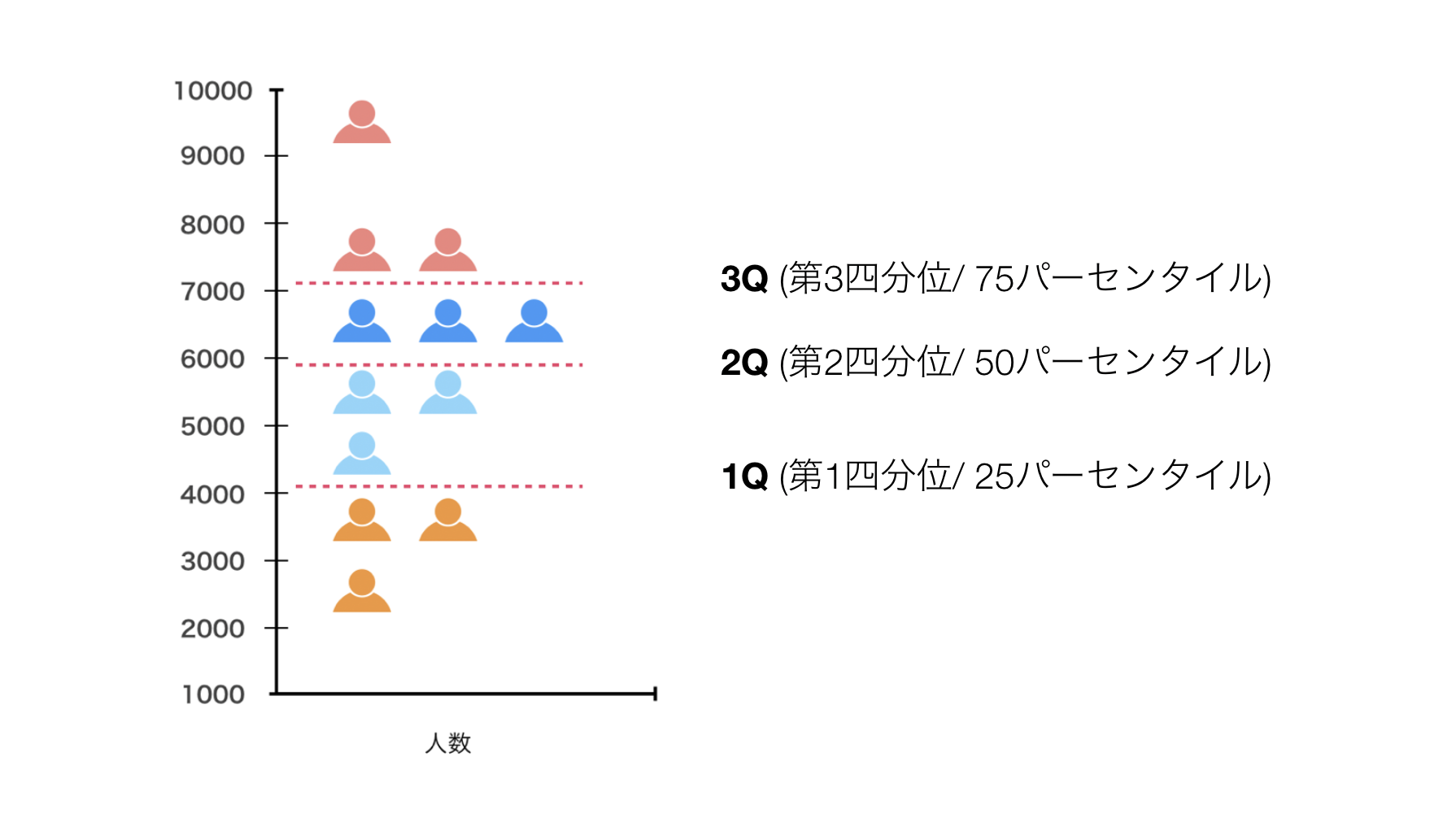
これらの線を覚えておいてください！

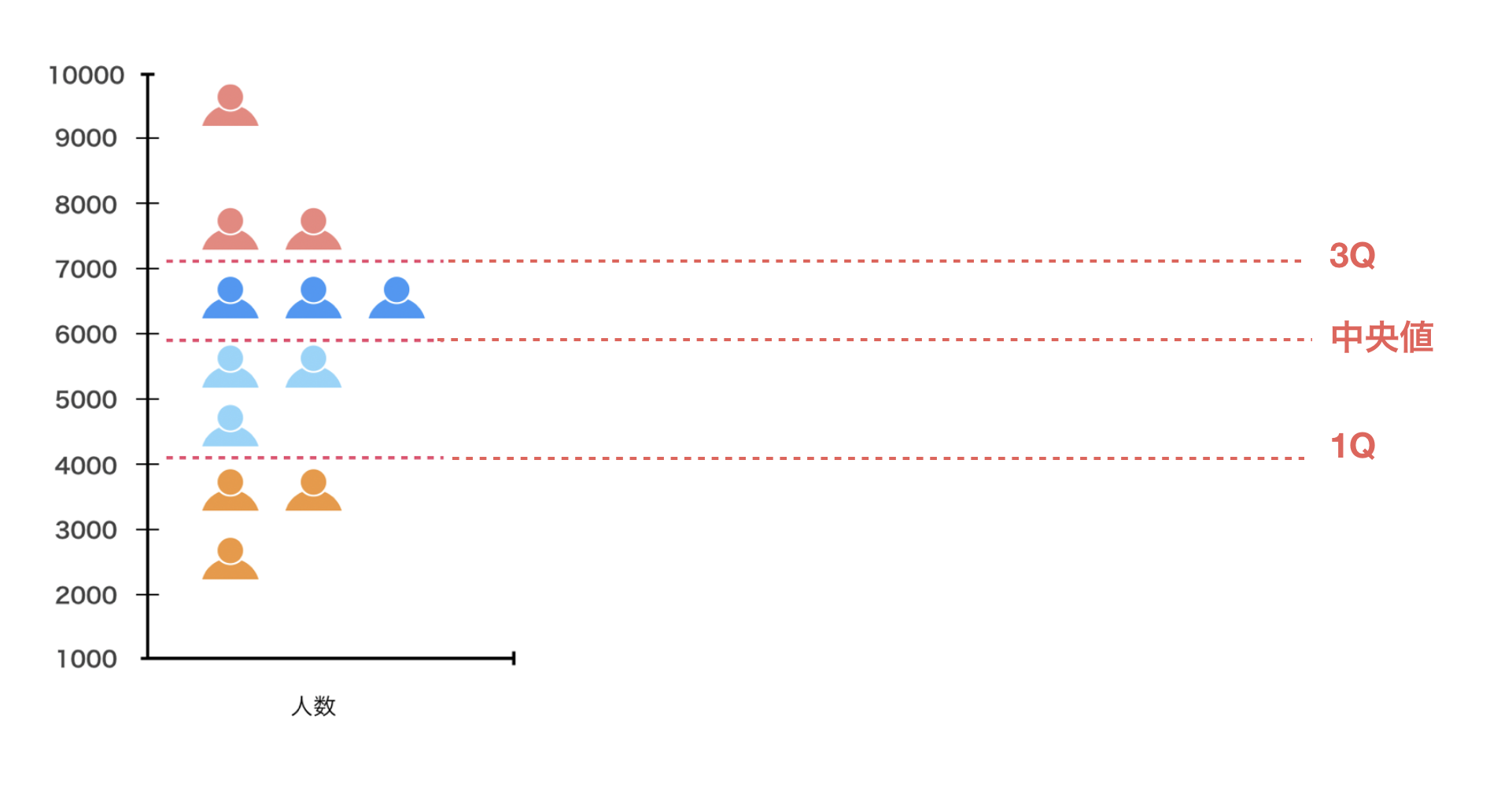
実は、箱ヒゲ図の箱は1Qと3Qの長さに相当し、箱の中に引かれる線は中央値となります。

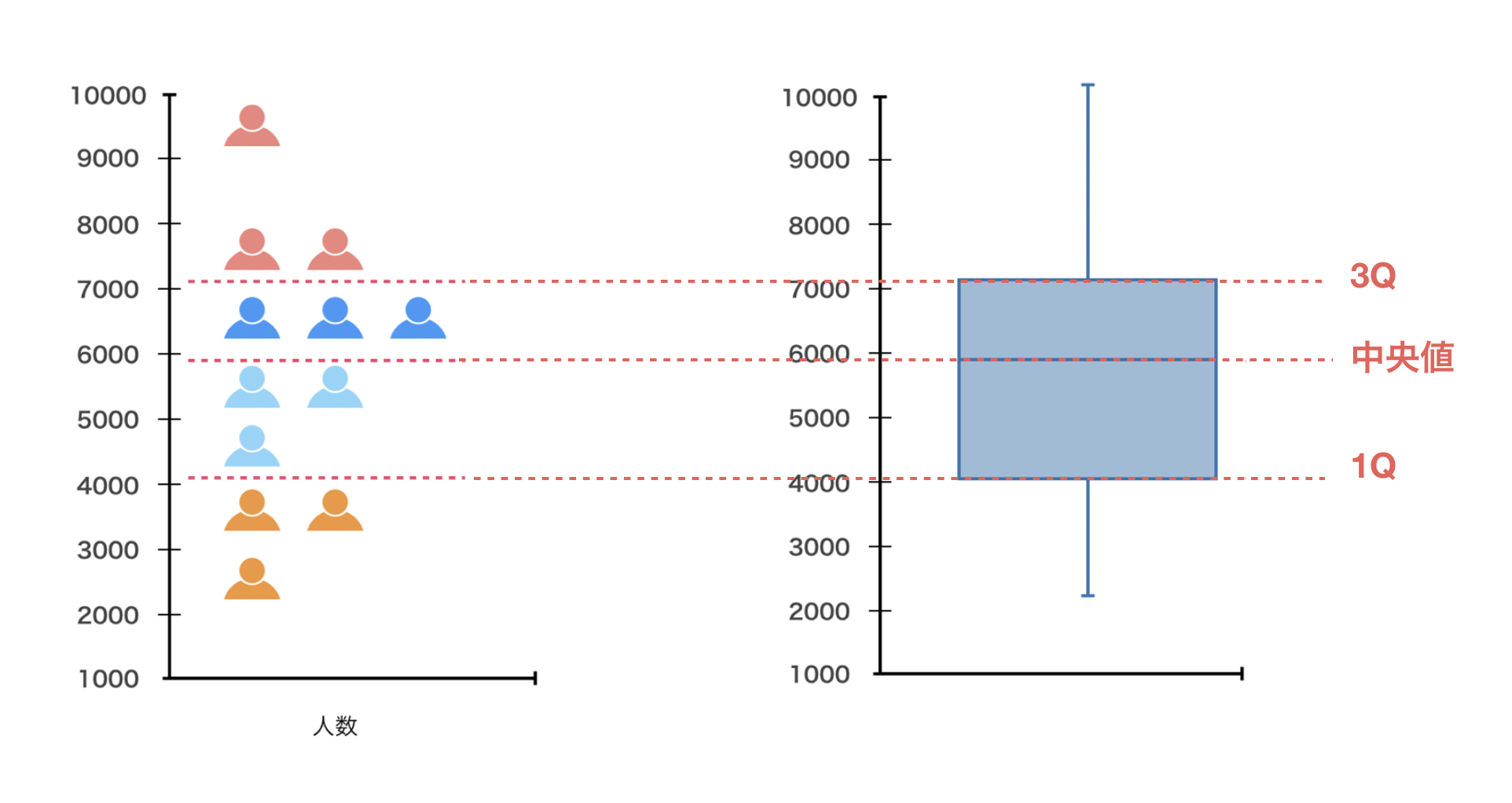
ちなみに、箱ヒゲ図のヒゲの部分は上が最大値、下が最小値となります。

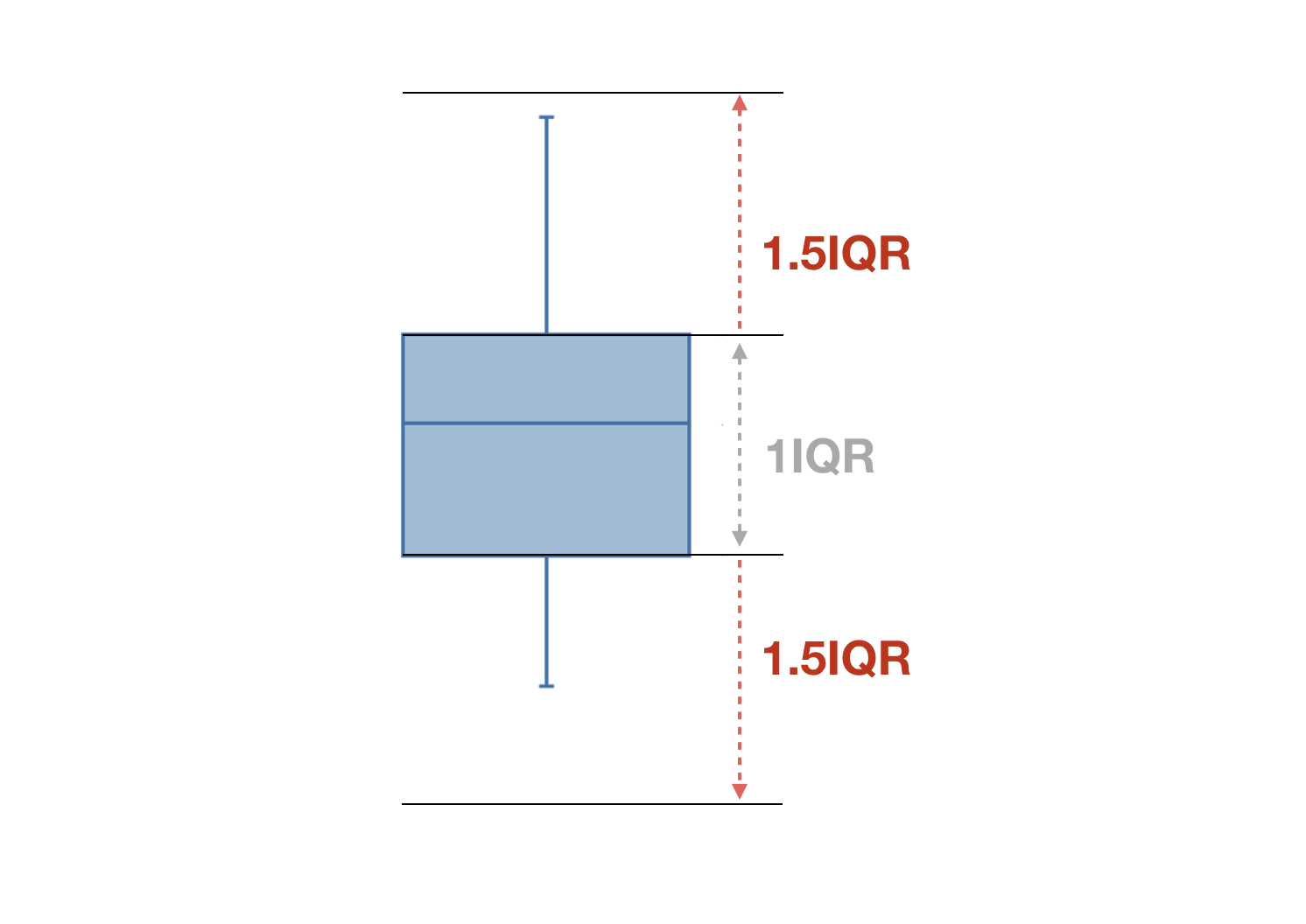
この箱ヒゲ図の1Q(25パーセンタイル)から3Q(75%パーセンタイル)の範囲を四分位範囲(IQR) と呼びます。

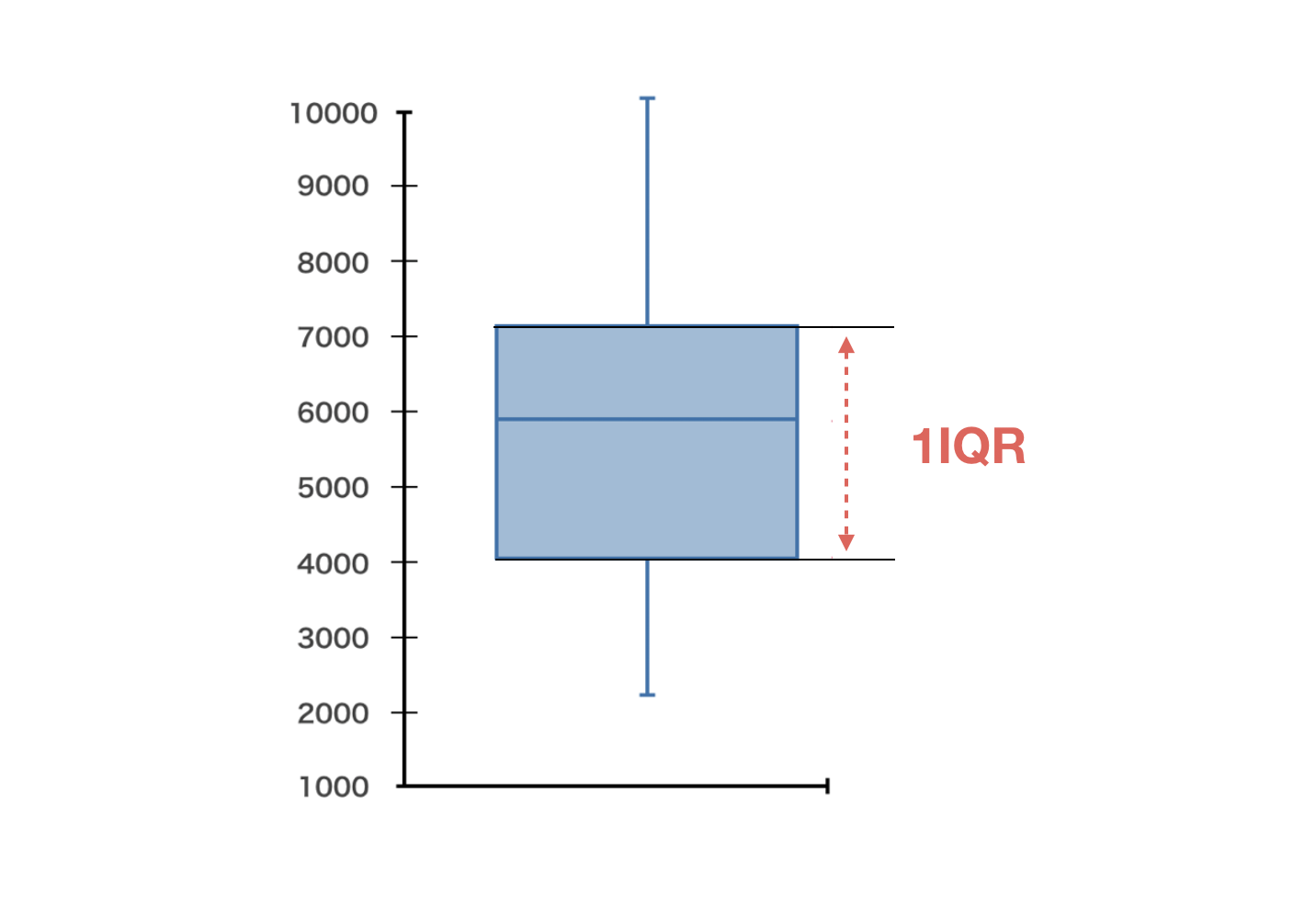
そして四分位範囲を使って外れ値を探す時には、箱の上端(3Q)から上に1.5IQR、箱の下端(1Q)から下に1.5IQRの範囲より外側の値が外れ値となります。

※1.5IQRとはIQRに1.5倍した値のことです。

四分位範囲(IQR)を使って外れ値を探す

こちらも給料の列を元に、四分位範囲(IQR)を使って外れ値のラベルを作りヒストグラムの色に割り当てます。

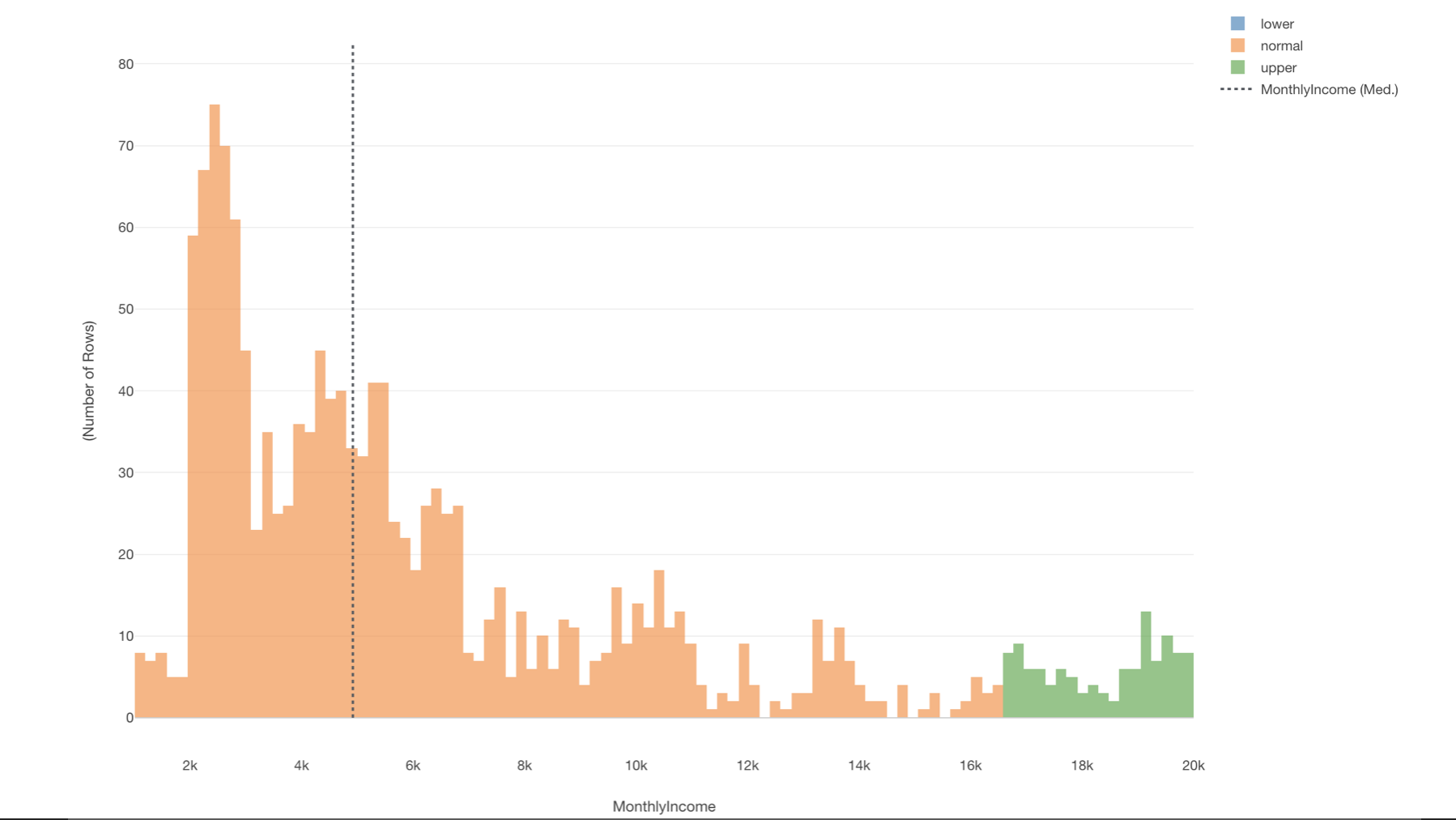
今回のデータでは、給料が異常に低い従業員はいませんでしたが、給料が異常に高い人たちは何人かいることがわかります。

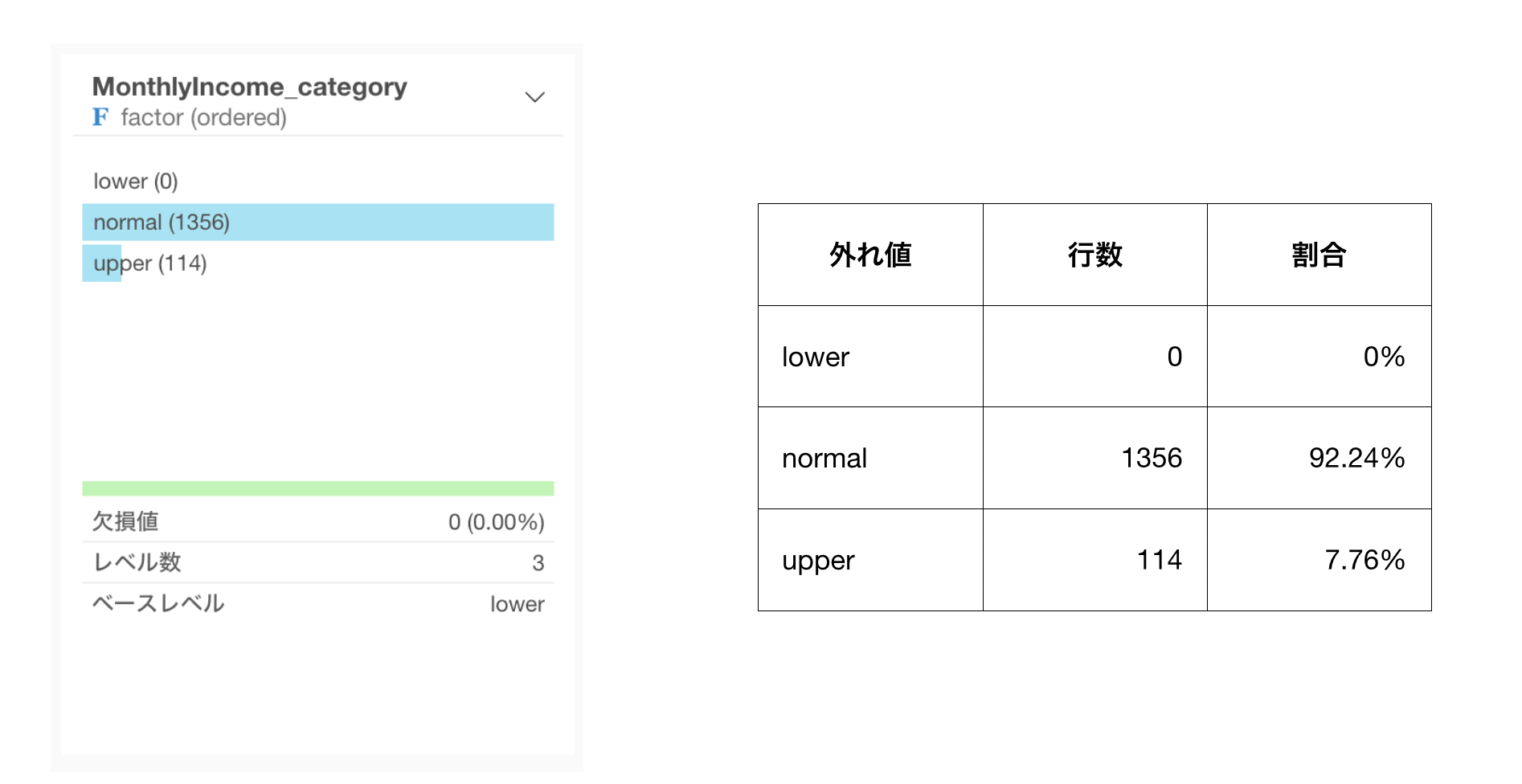
サマリ・ビューで確認してみると、給料が異常に高い人は114人いて、全体の7.76%ということがわかりました。

ビンを使って給料が外れ値の従業員にラベルを付ける

これまで、外れ値の問題点と外れ値検知のタイプについて説明してきましたが、実際に外れ値のラベルをつけていきます。

Exploratoryではビン(カテゴリー)を作成という機能を使うことで簡単に外れ値のラベルをつけることができます。

MonthlyIncome(給料)の列ヘッダメニューからビン(カテゴリー)を作成を選択します。

ビン(カテゴリー)を作成のダイアログが開くので、手法に外れ値を選択します。

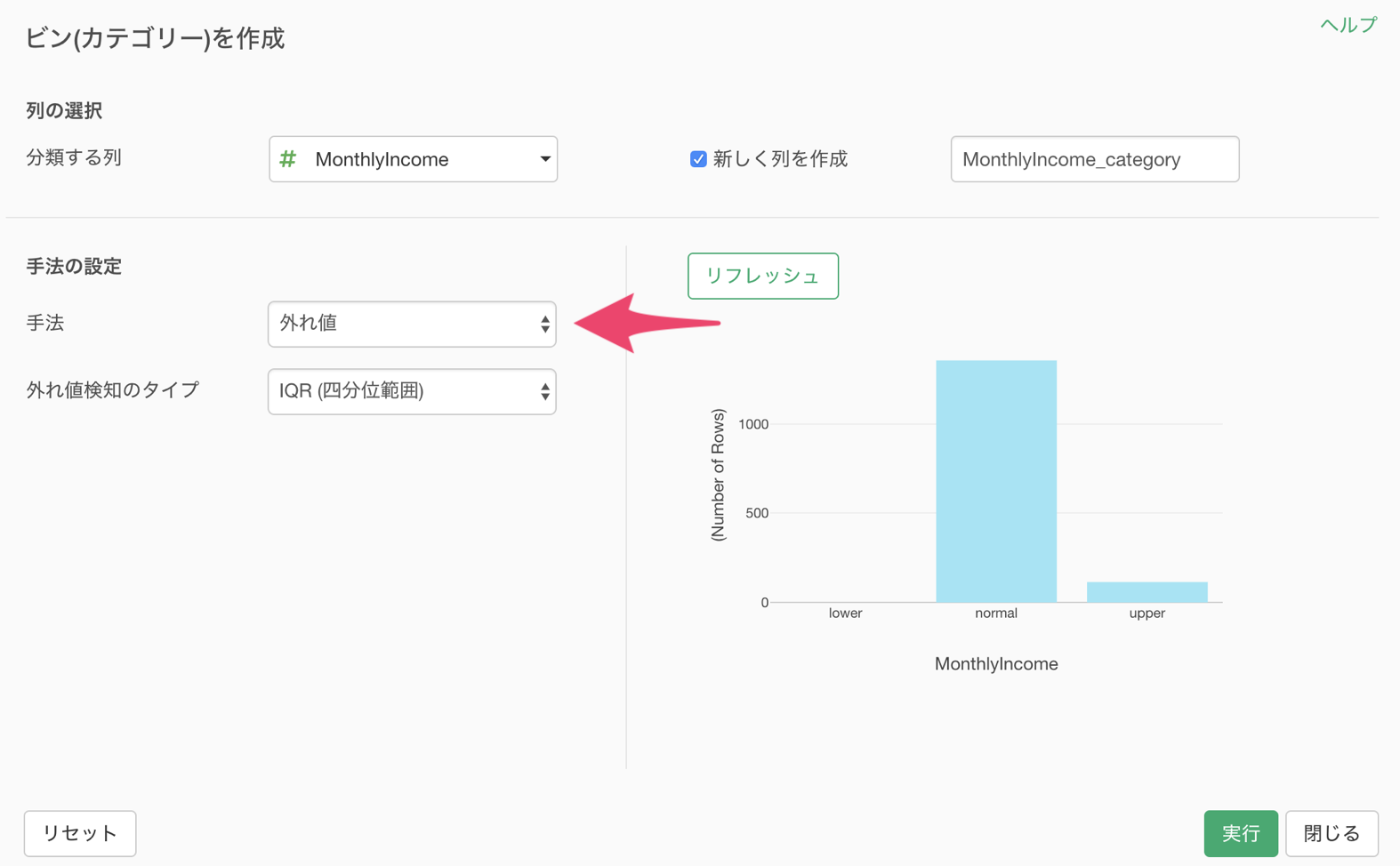
外れ値検知のタイプには先ほど説明した3つのタイプがあります。

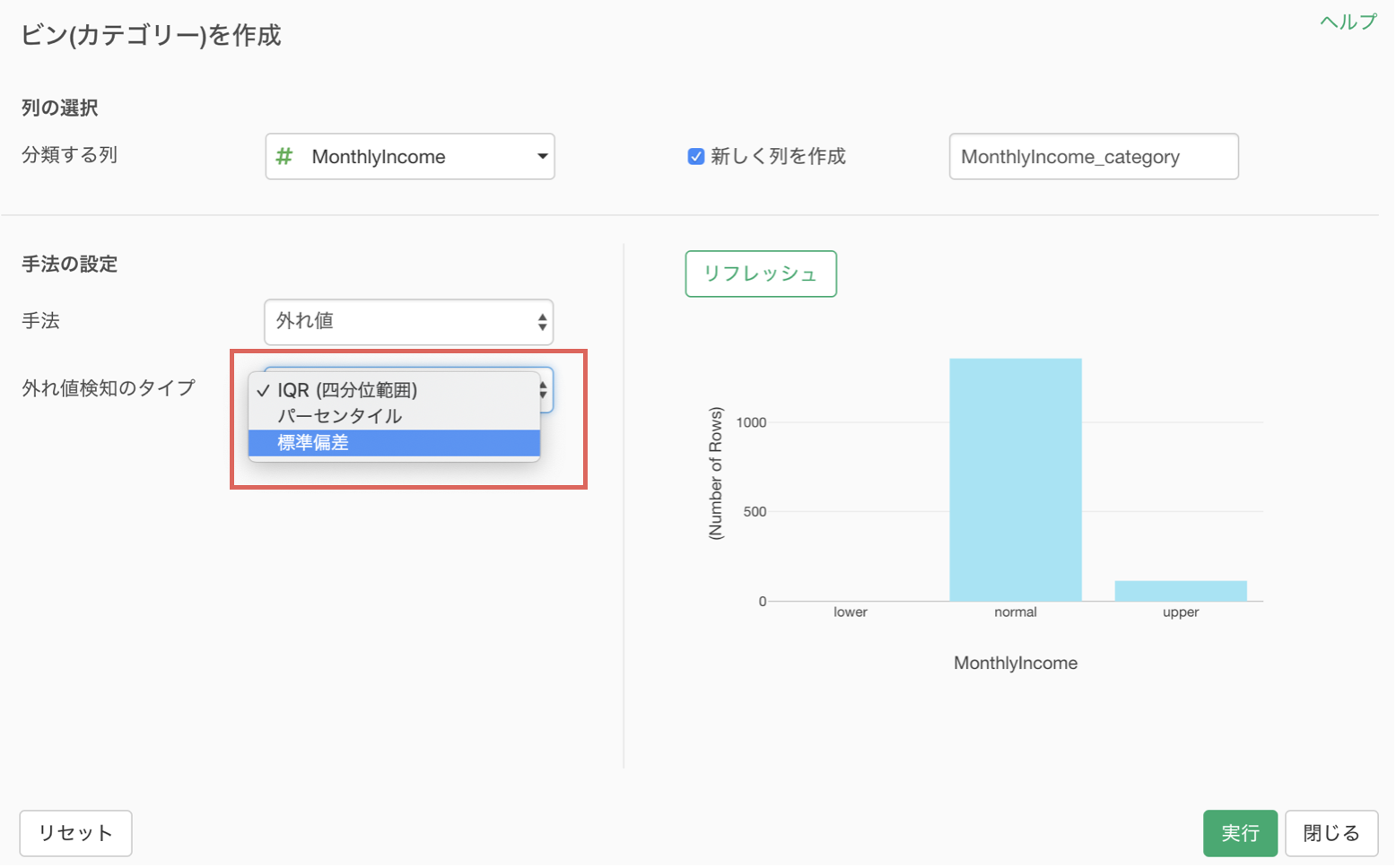
今回は、外れ値検知のタイプに標準偏差を選び、しきい値に2を指定します。

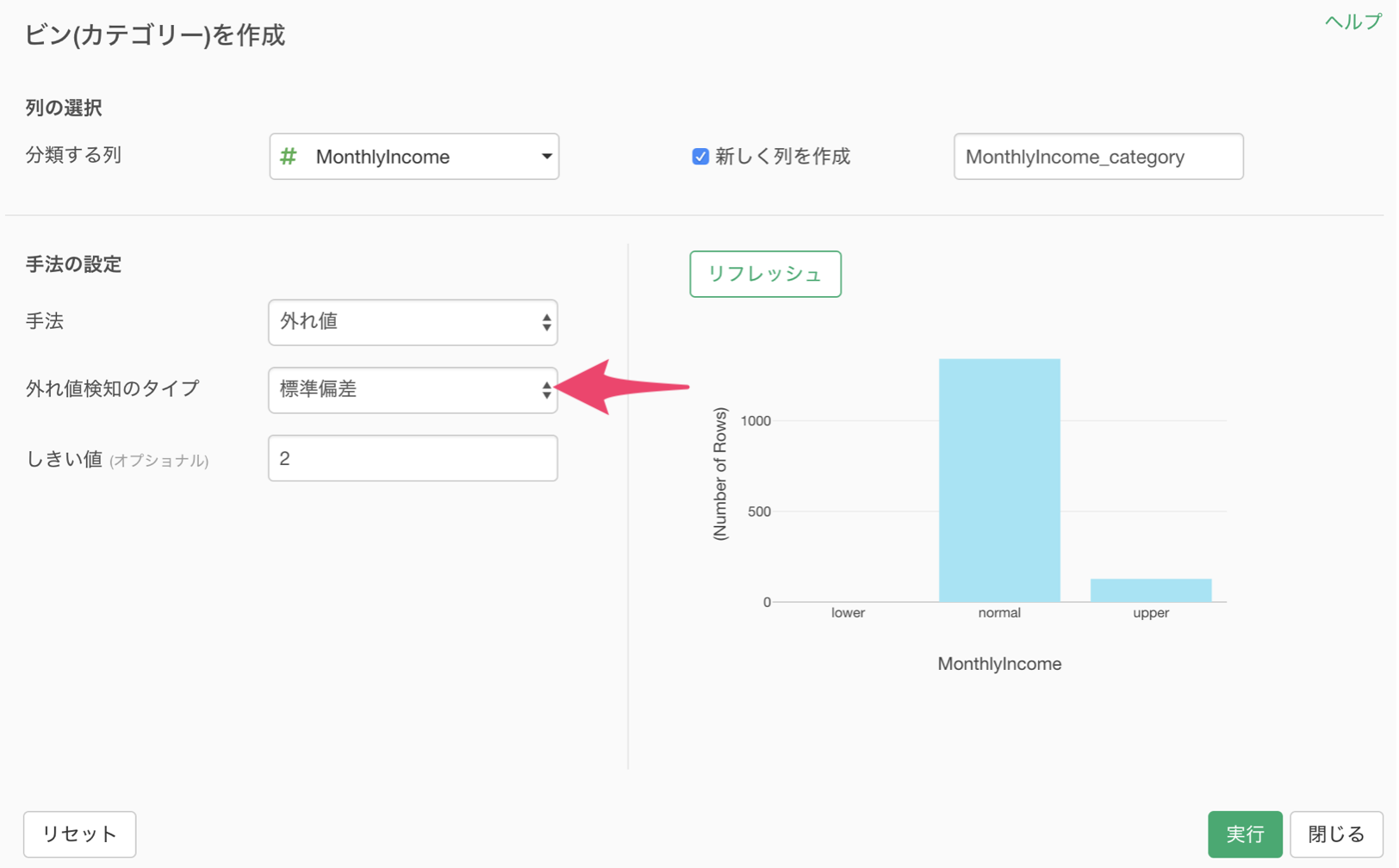
リフレッシュボタンを押すことで、バーチャート（カテゴリー化された値の行数）を最新の状態にすることができます。

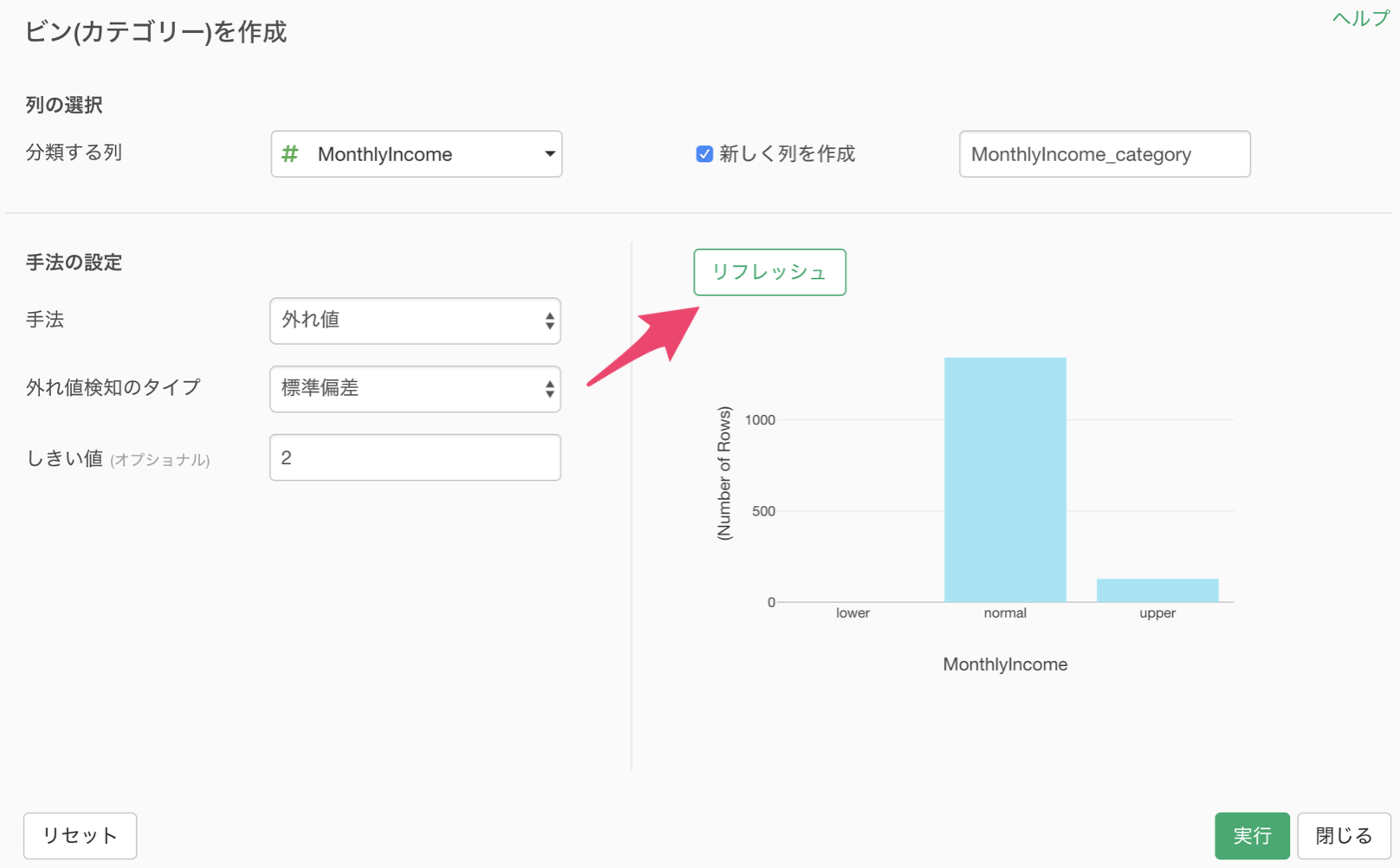
実行すると従業員の給料が外れ値かどうかのラベルを付けることができました！

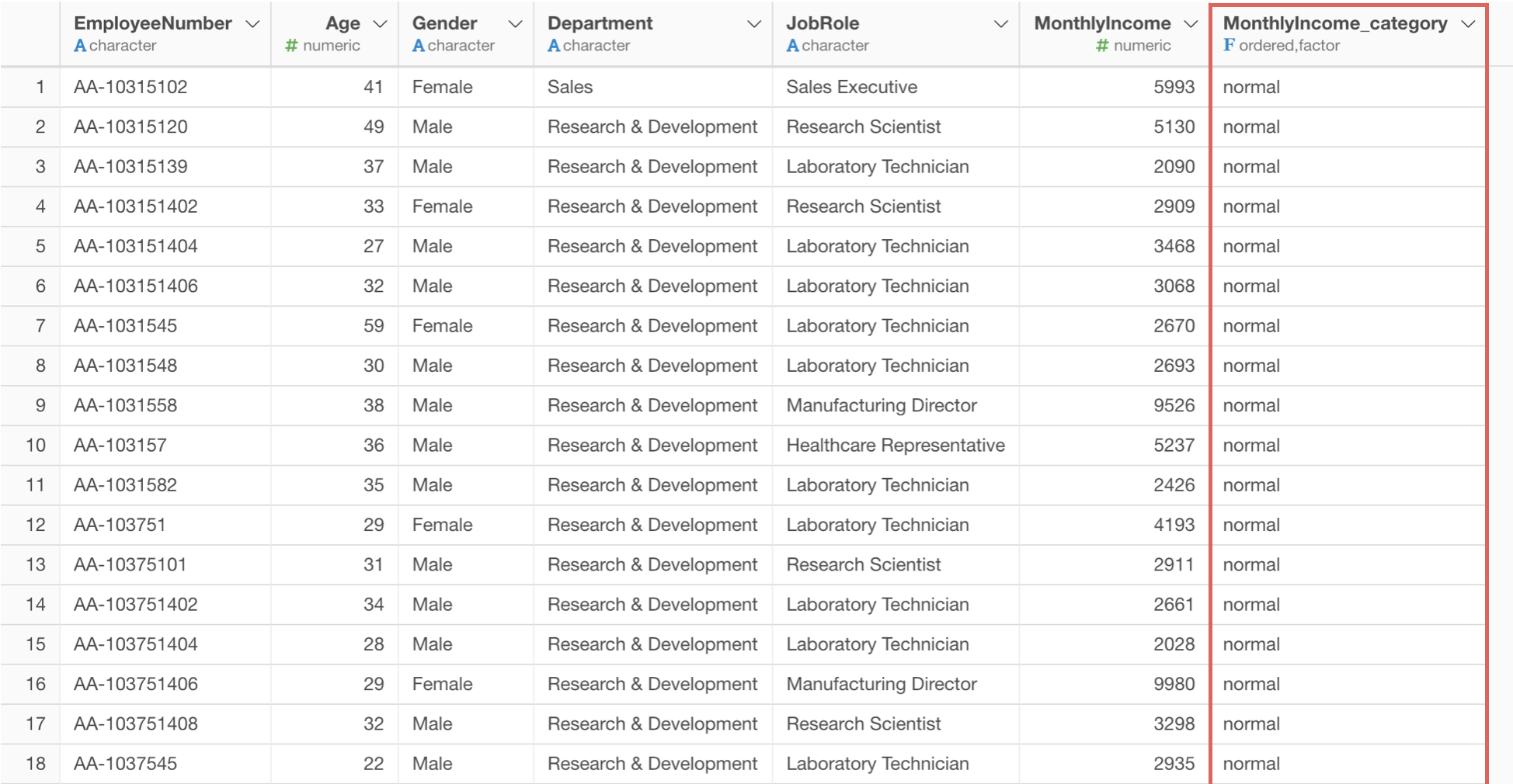
サマリ・ビューで確認してみると、給料が異常に低い人はいませんが、異常に高い人は 128人いることがわかります。

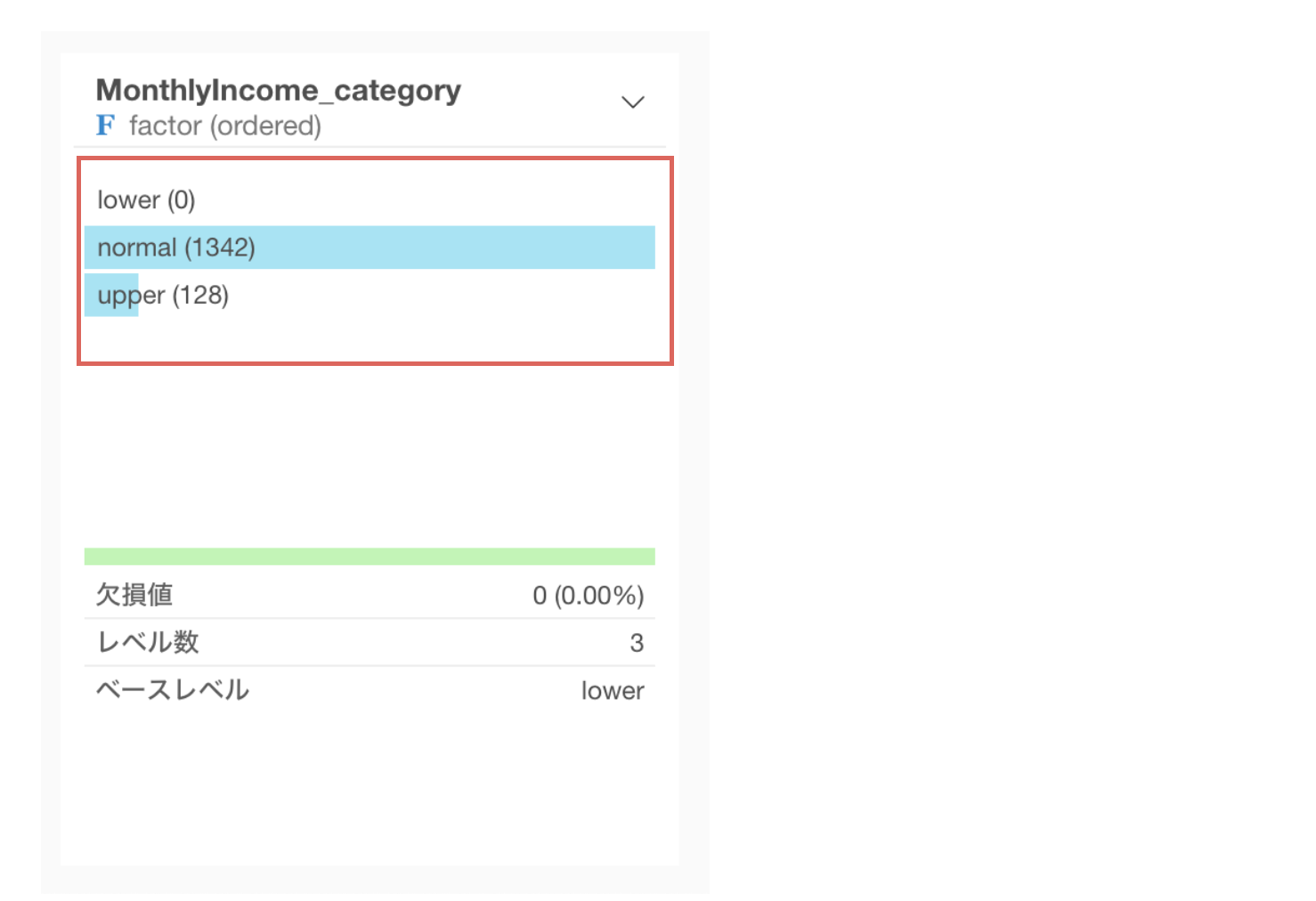
フィルタを使って外れ値を取り除く

外れ値のラベルを付けることができたら、あとはフィルタを使って外れ値のデータを取り除くことができます。

外れ値かどうかの列ヘッダメニューからフィルタを選び、等しいを選択します。

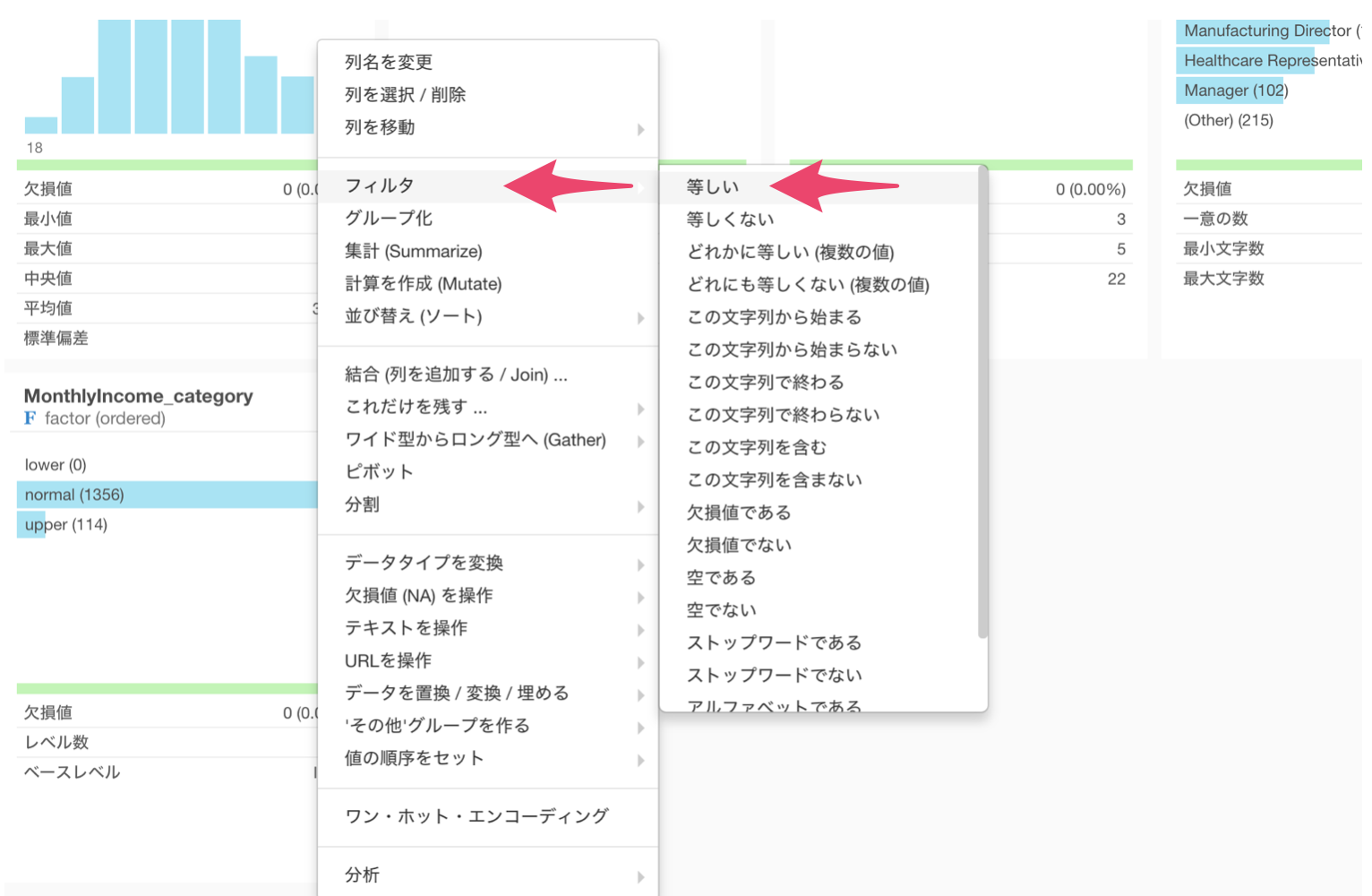
演算子に等しいを選び、値にはnormalを選択します。

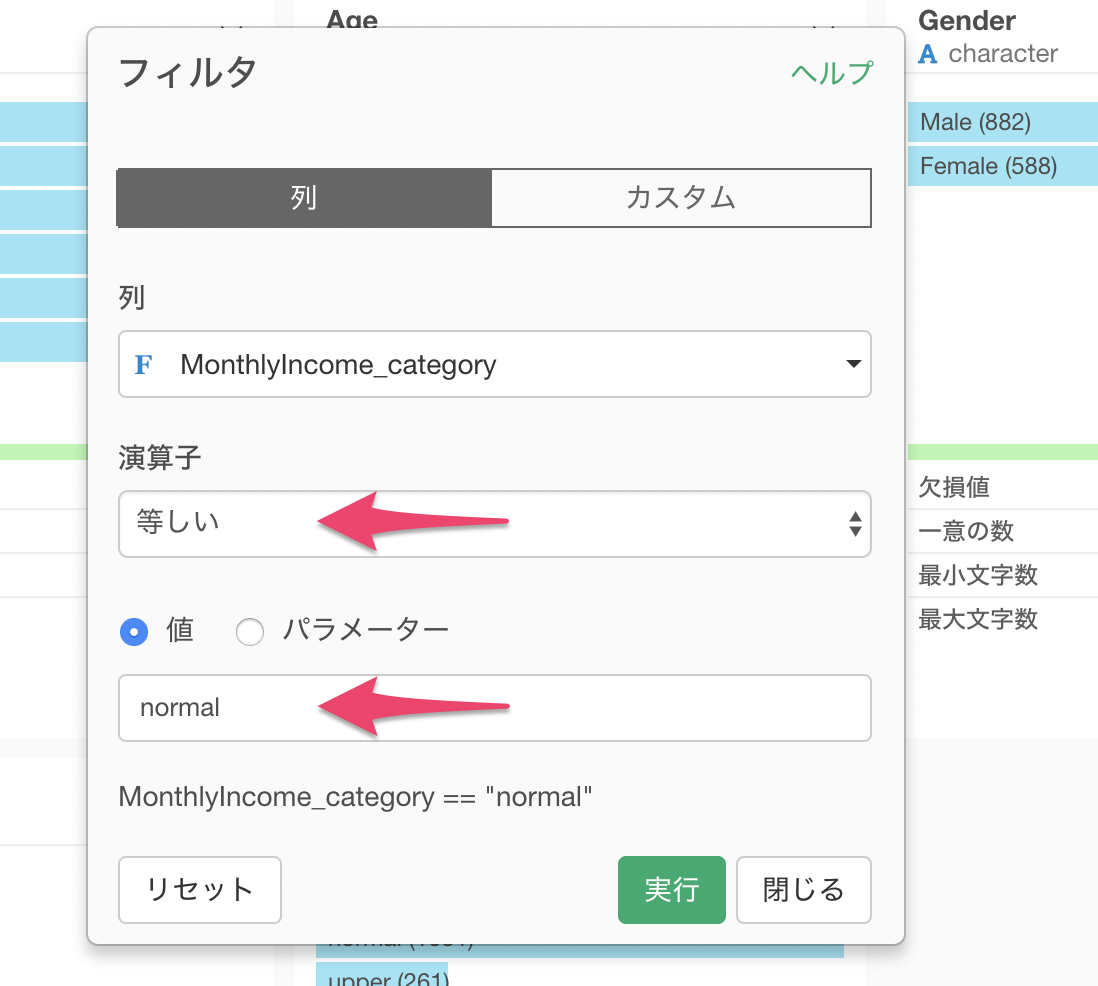
フィルタを使って外れ値でないデータのみを残すことができました。

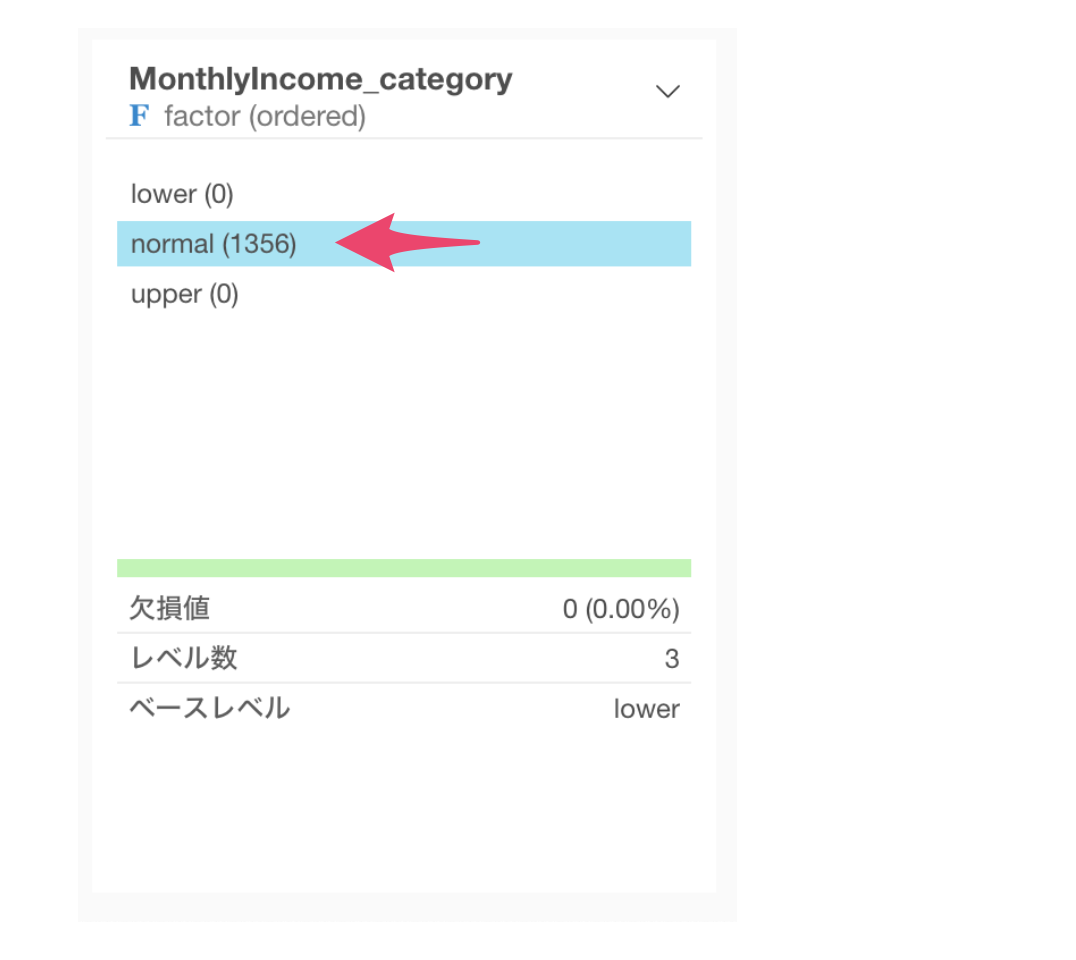
チャートの中で外れ値を判別する

実は、外れ値を可視化したいだけであればチャートの中で簡単にみていくことができます。

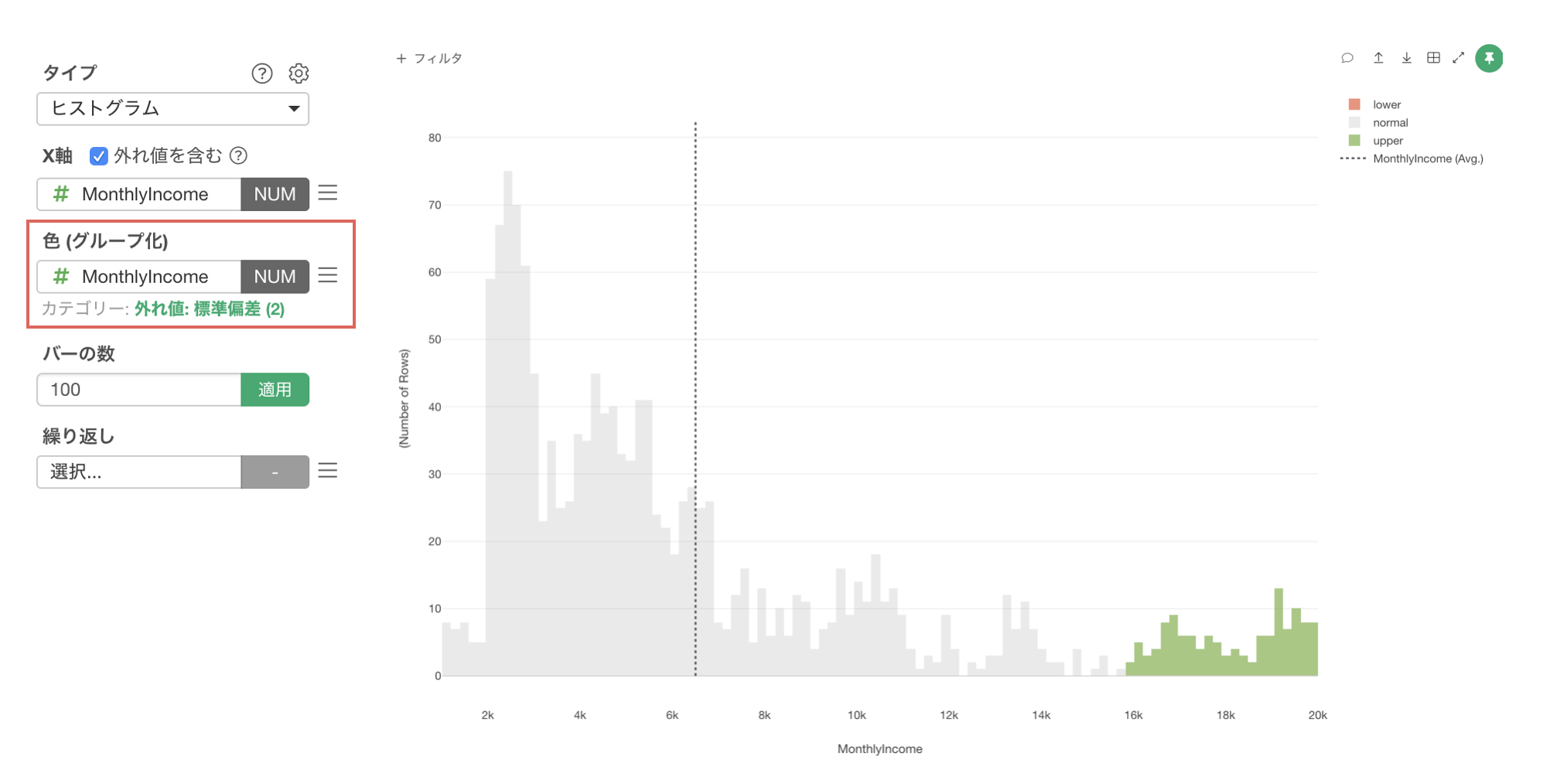
まず、X軸にMonthlyIncomeを割り当てて、バーの数を100にします。

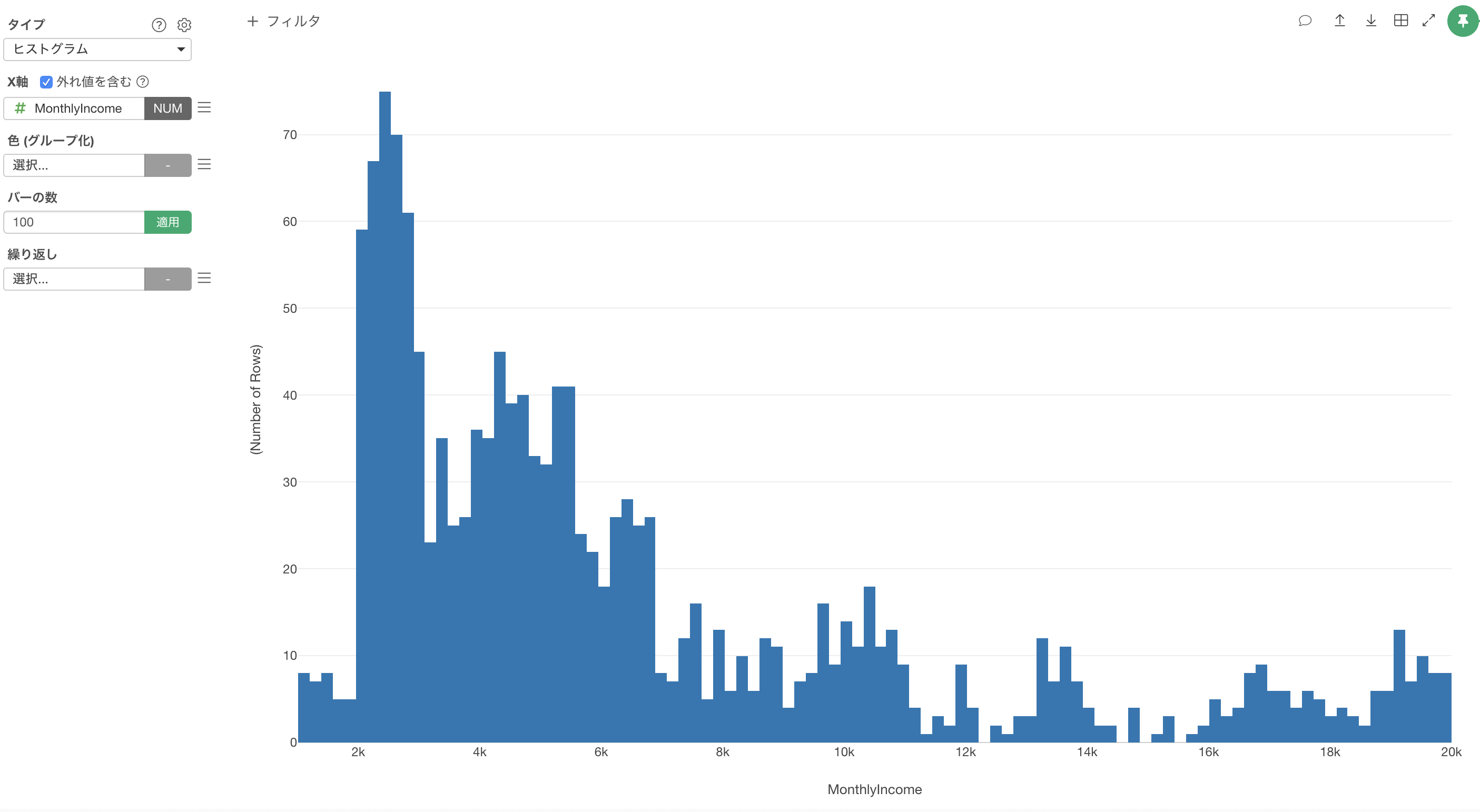
次に、色 (グループ化)にもMonthlyIncomeを割り当てます。

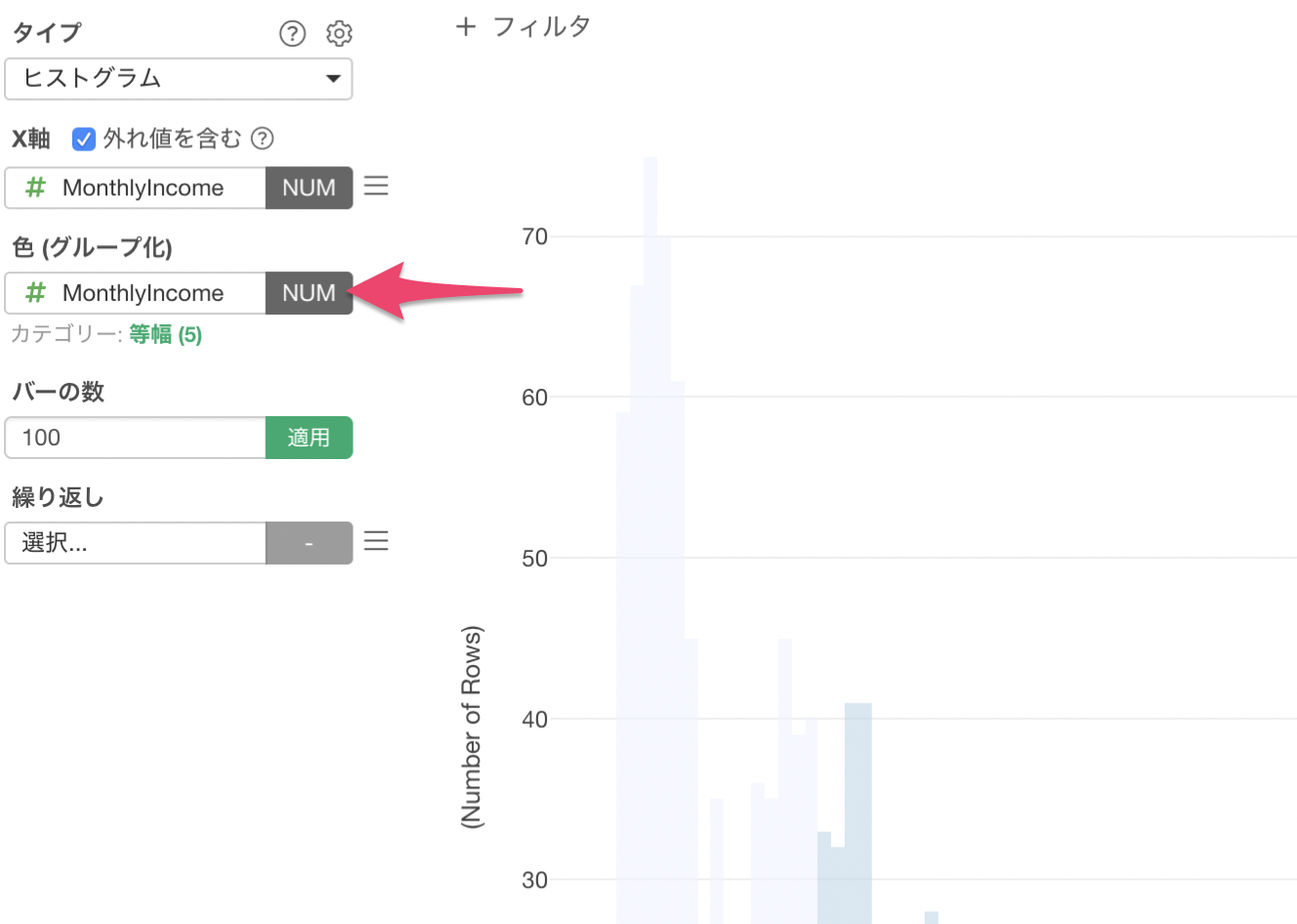
色に対して数値を割り当てた際、デフォルトでカテゴリー化されます。

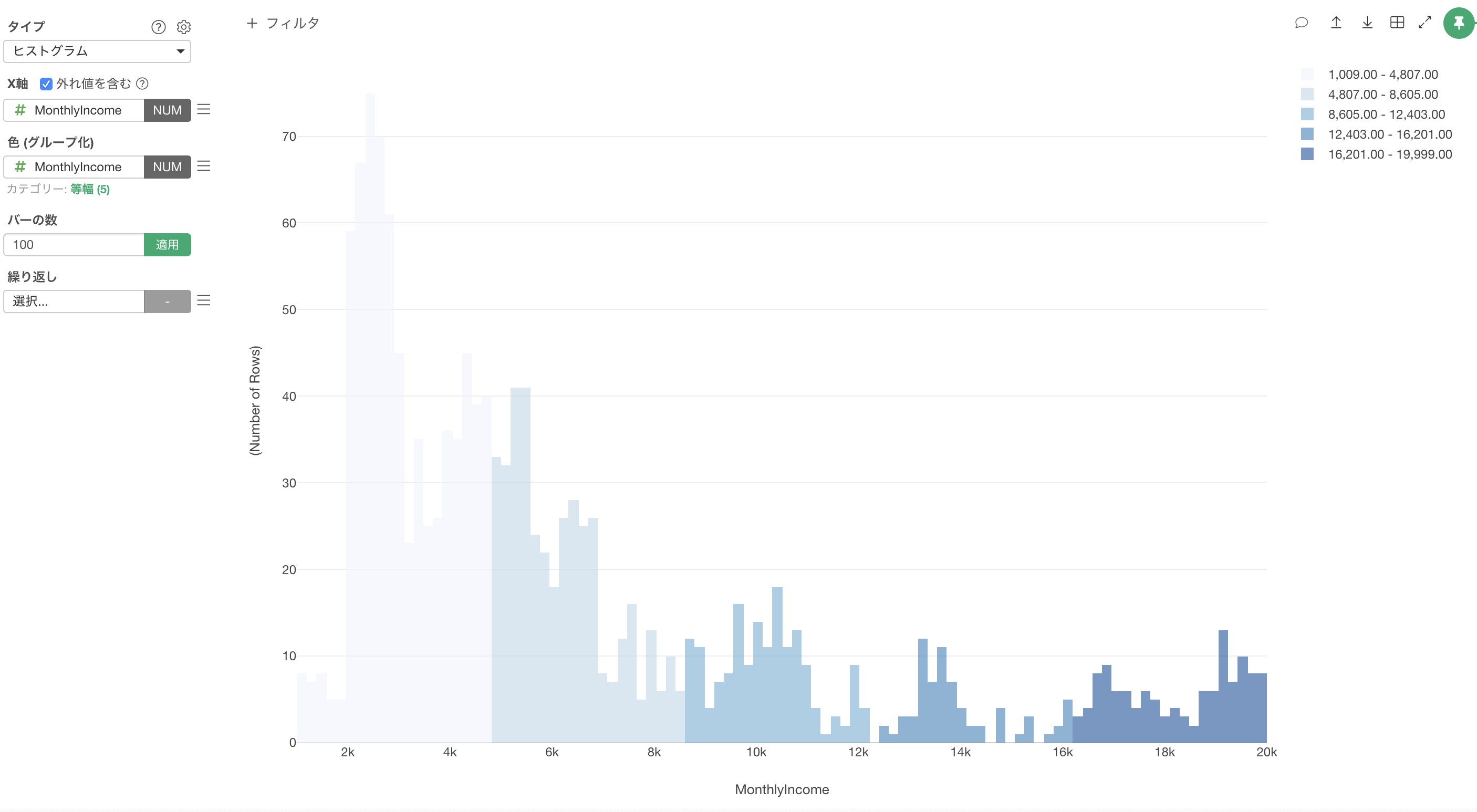
タイプが等幅になっているので、「等幅 (5)」と緑の文字で表示されているところをクリックします。

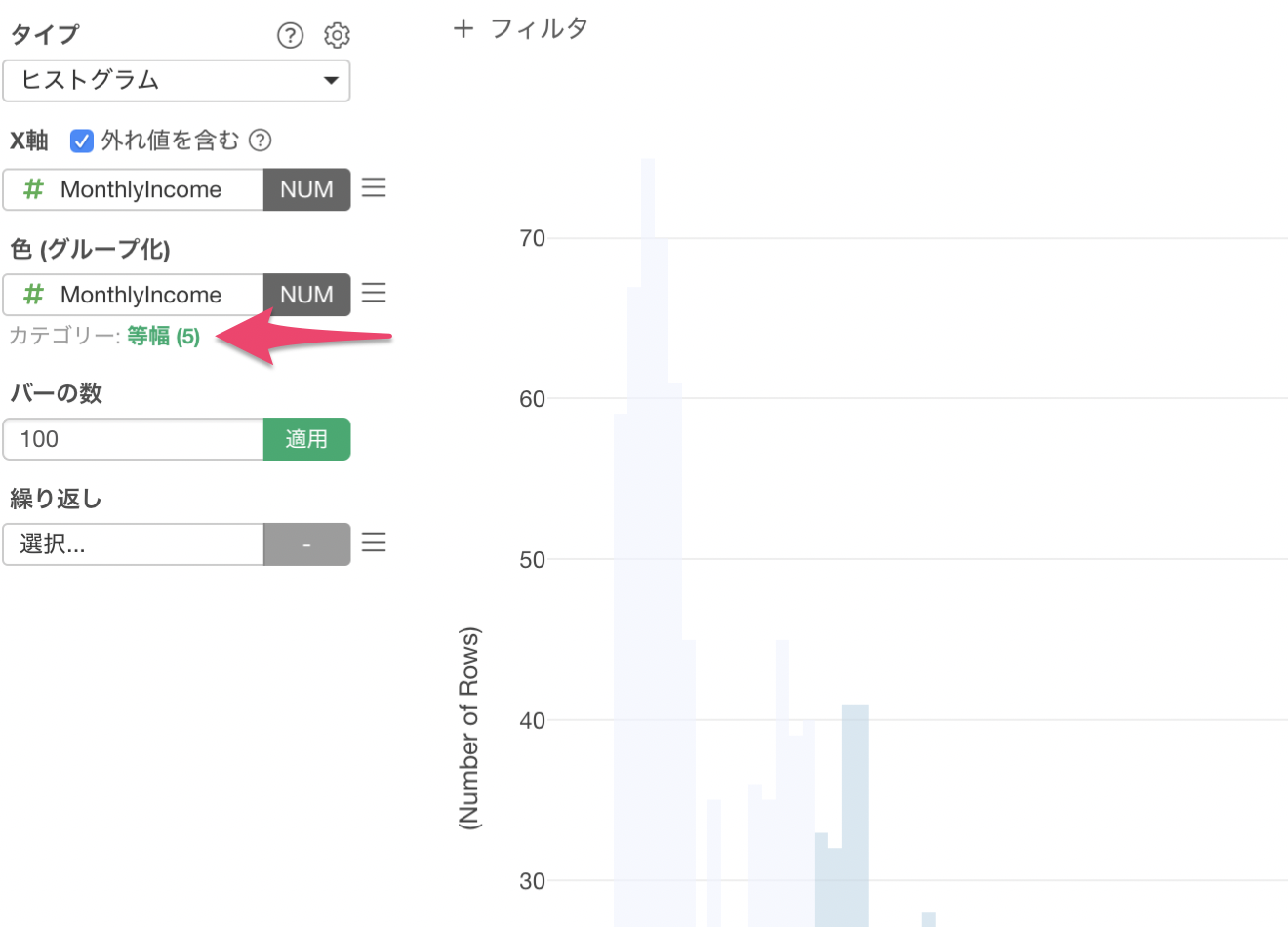
タイプに外れ値を選び、外れ値のタイプは標準偏差を選択します。

しきい値はデフォルトで2となっているので、このまま適用ボタンをクリックします。

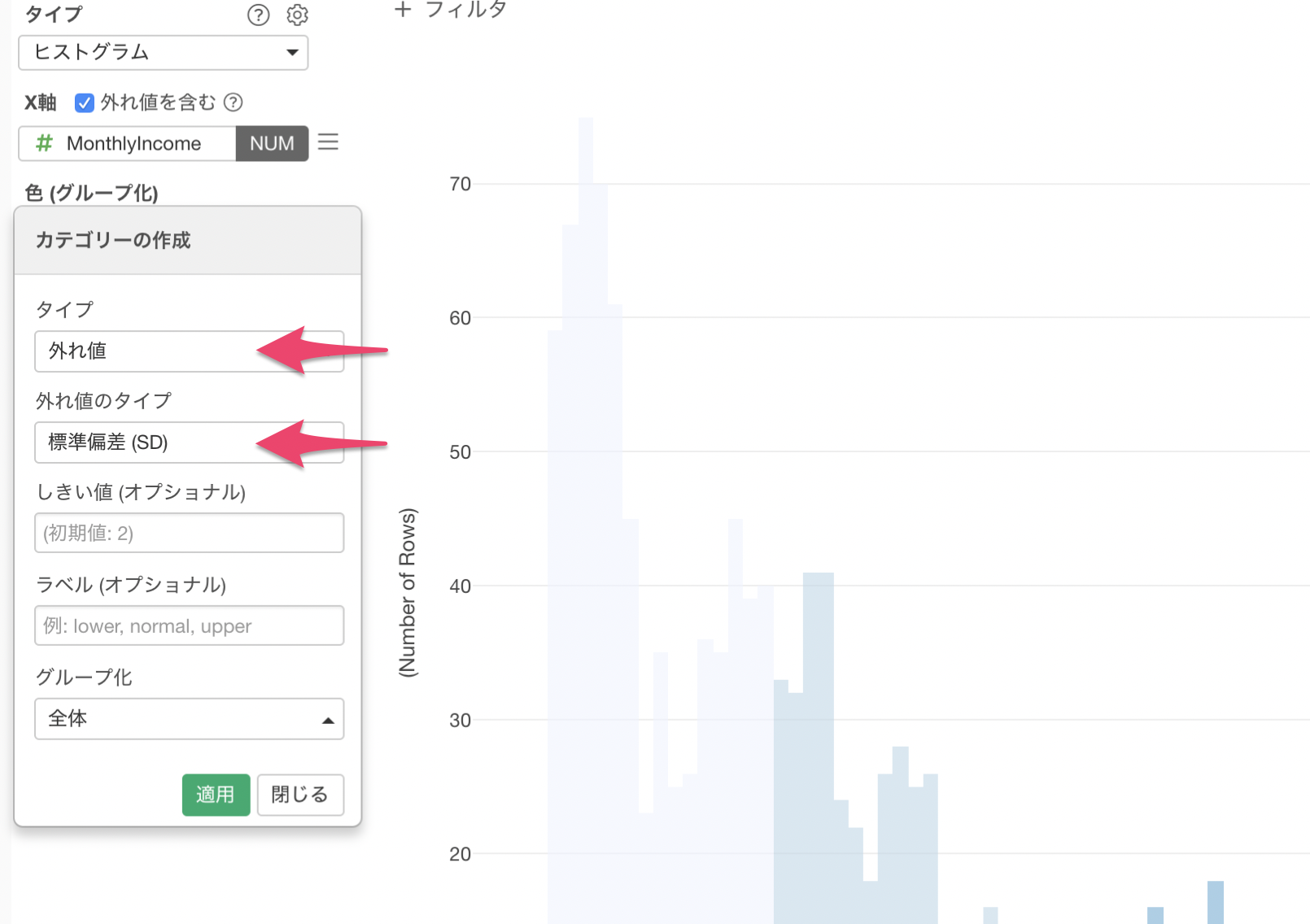
チャート内で色を使って外れ値で判別することができました。