ANCOVA(共分散分析)の使い方
ANCOVAは共分散分析(Analysis of Covariance)の略称で、分散分析の拡張として位置づけられる統計手法です。通常の分散分析(ANOVA)では、カテゴリ変数(要因)が目的変数に与える影響を分析しますが、ANCOVAではそれに加えて、連続変数(共変量)の影響も同時に考慮することができます。これにより、より精緻な分析が可能となり、カテゴリ変数の「純粋な効果」を見極めることができます。
たとえば、社員研修の効果を分析する場合、単純に部署間で研修後のスコアを比較するだけでなく、研修前のスコアという連続変数の影響を調整した上で、部署による違いを検証することができます。これにより、研修前の能力の違いを考慮した上で、純粋な研修効果の違いを評価することが可能になります。また、複数のグループ間で比較を行う際に、初期状態の違いによる影響を統計的に制御することで、より公平で正確な比較が可能になります。
ANCOVAの特徴的な点は、共変量による調整を行った後の「調整済み平均値」を算出できることです。これは、共変量の影響を統計的に均一にした場合に予測される各グループの平均値を表しており、純粋な要因の効果を理解する上で非常に有用な指標となります。また、この手法は実験計画法においても重要な役割を果たし、実験前の状態や外部要因の影響を考慮した上で、処置の効果を正確に評価することを可能にします。
1. どういった時に使えるのか
ANCOVAは、グループ間の比較を行う際に、連続変数の影響を考慮する必要がある場面で特に有効です。例えば、新しい教育プログラムの効果を検証する際、単にプログラム実施後のテストスコアを比較するだけでなく、実施前のテストスコアという連続変数の影響を調整した上で、プログラムの純粋な効果を評価することができます。また、健康増進プログラムの効果を検証する際には、参加者の年齢や運動習慣といった連続変数の影響を考慮した上で、プログラムの真の効果を測定することが可能です。
特に、初期状態や背景要因に大きな違いがある場合、それらの影響を統計的に制御することで、より正確な比較が可能になります。例えば、異なる教育機関での学習効果を比較する際、生徒の入学時の学力や家庭環境などの要因を考慮することで、教育機関の純粋な効果を評価することができます。また、マーケティングキャンペーンの効果を分析する際にも、顧客の過去の購買履歴や年収などの連続変数の影響を調整した上で、キャンペーンの真の効果を測定することが可能です。
参考となるデータ例:
- 教育効果データ:プログラム種別、事前テストスコア、事後テストスコア、学習時間
- 健康プログラムデータ:プログラム種別、開始時の体重、終了時の体重、年齢、運動時間
- 営業研修データ:研修タイプ、研修前売上、研修後売上、営業経験年数
- マーケティングデータ:キャンペーン種別、過去の購買額、キャンペーン後の購買額、顧客年数
2. ユースケース
教育業界での使い方
- 教育機関では、新しい教育プログラムの効果を検証する際に使えます。
- 具体的には、学生の事前の学力レベルを考慮した上で、異なる教育プログラムによる学習効果の違いを分析する際にANCOVAを使うことで、純粋な教育プログラムの効果を把握することができます。
- これにより、各教育プログラムの効果を正確に評価し、より効果的な教育プログラムの開発や改善に活かすことができます。
医療業界での使い方
- 医療機関では、異なる治療法の効果を比較する際に使えます。
- 具体的には、患者の年齢や初期症状の重症度を考慮した上で、治療法の違いによる回復度合いを分析する際にANCOVAを使うことで、純粋な治療効果の違いを把握することができます。
- これにより、患者の特性を考慮した上で最適な治療法を選択する際の科学的根拠を得ることができます。
人事担当者での使い方
- 人事部門では、研修プログラムの効果を評価する際に使えます。
- 具体的には、従業員の経験年数や研修前のスキルレベルを考慮した上で、異なる研修方法による成果の違いを分析する際にANCOVAを使うことで、純粋な研修効果を把握することができます。
- これにより、より効果的な研修プログラムの設計や、個々の従業員に適した研修方法の選択に活かすことができます。
マーケティング担当者での使い方
- マーケティング部門では、プロモーション施策の効果を測定する際に使えます。
- 具体的には、顧客の過去の購買履歴や会員継続年数を考慮した上で、異なるプロモーション手法による売上への影響を分析する際にANCOVAを使うことで、純粋なプロモーション効果を把握することができます。
- これにより、顧客特性を考慮した上で最も効果的なプロモーション戦略を立案することが可能になります。
3. ExploratoryでANCOVA (共分散分析)を実行する
使用するデータ
今回は「社員研修効果分析データ」を使用します。このデータはサンプルデータとして、こちらからダウンロードが可能となっています。
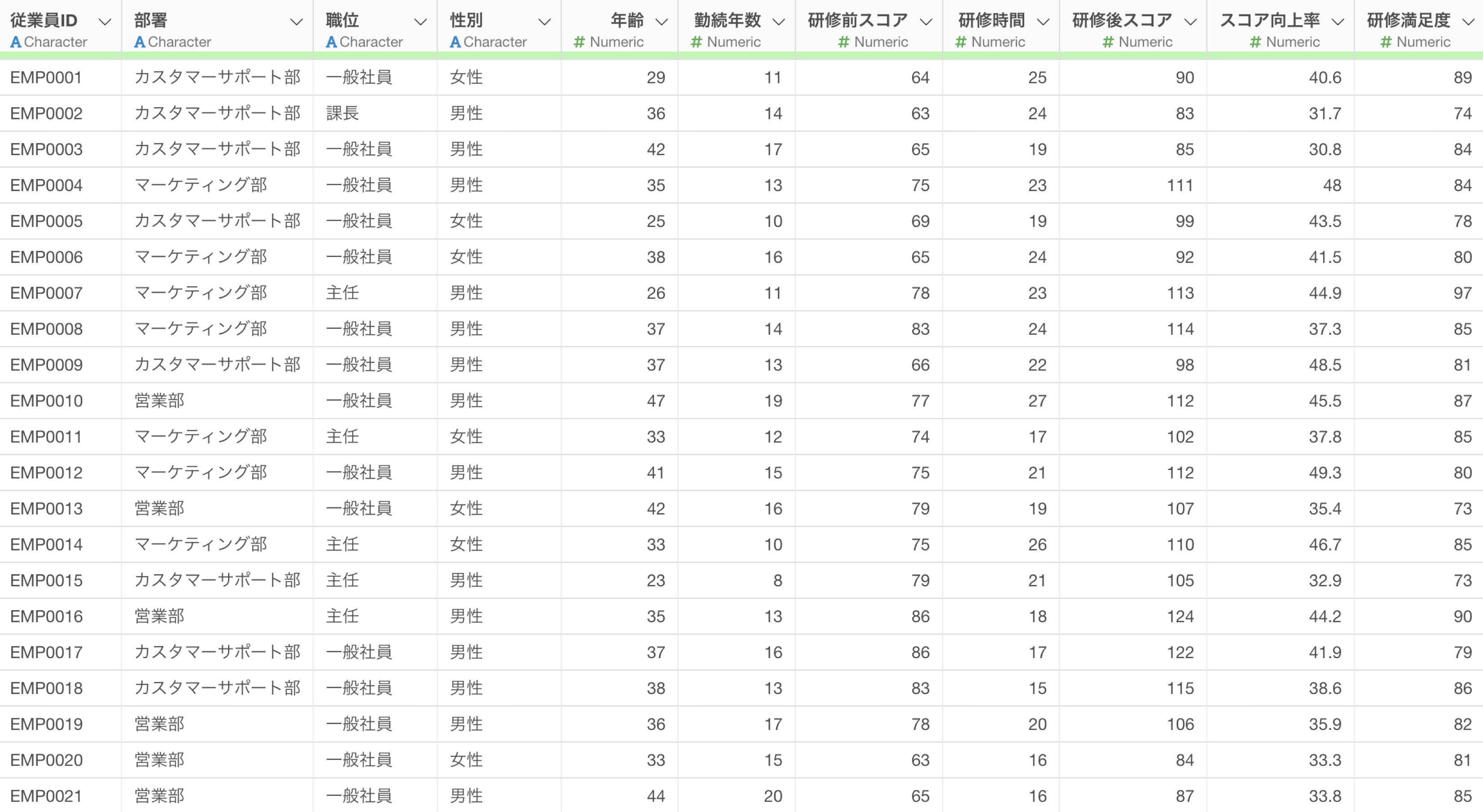
このデータは1行が1名の従業員の研修データを表しており、列には「従業員ID」「部署」「研修前スコア」、「研修後スコア」などのデータがあります。
ANCOVA (共分散分析)を実行するためには、以下のようなデータの構造が必要となります。
- 目的変数が連続変数であること(例:研修後スコア)
- 説明変数がカテゴリ変数であること(例:部署)
- 共変数が連続変数であること(例:研修前スコア)
アナリティクスを作成する
社員研修効果分析データから「アナリティクス・ビュー」を開きます。
タイプに「統計的検定」を選び、「ANCOVA (共分散分析)」を選択します。
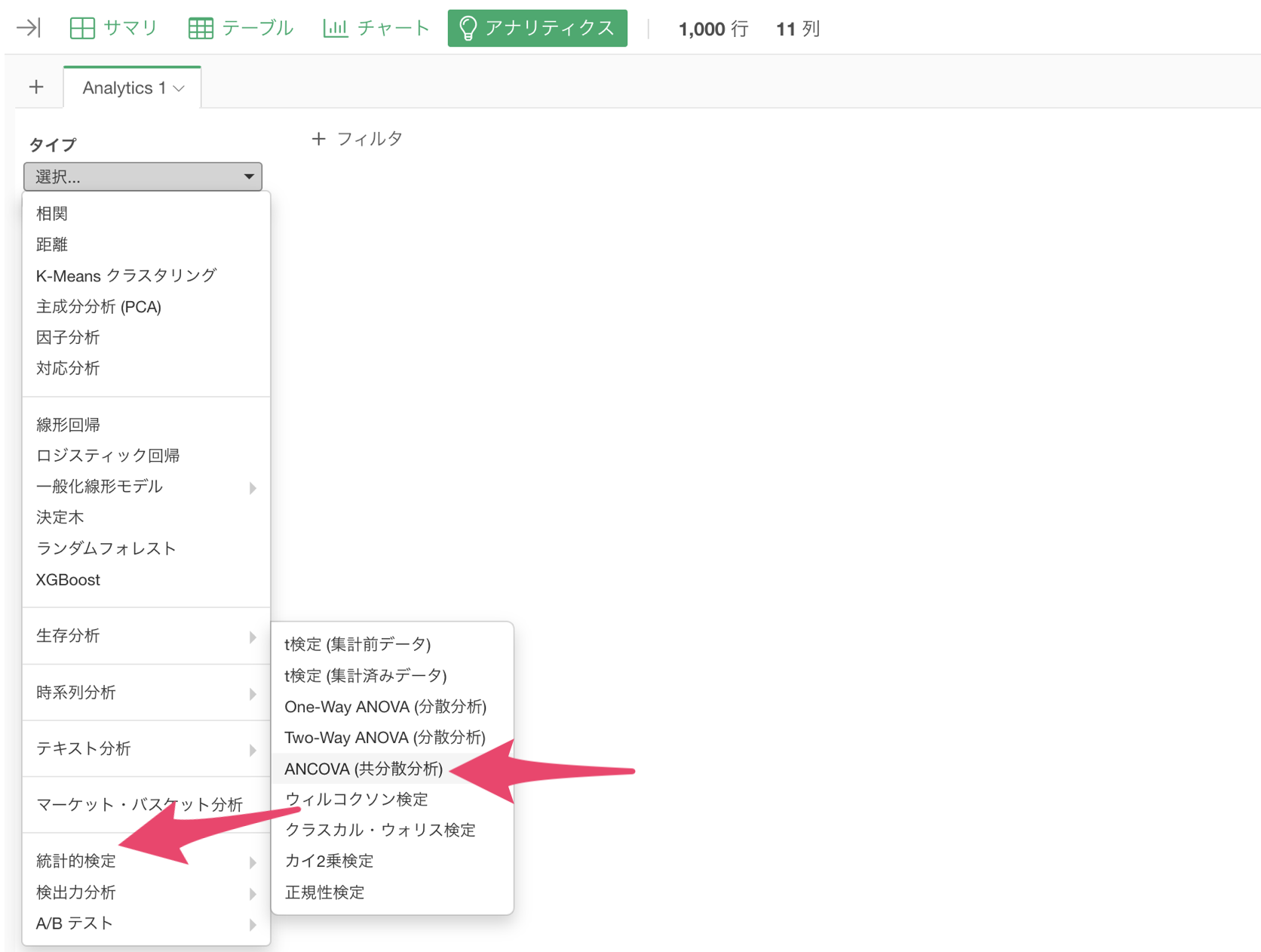
今回は以下のように列を指定します。
- 目的変数には「研修後スコア」の列を割り当てます。
- 説明変数には「部署」の列を割り当てます。
- 共変数には「研修前スコア」の列を割り当てます。
 最後に、「実行」ボタンをクリックして実行結果を確認します。
最後に、「実行」ボタンをクリックして実行結果を確認します。
結果の解釈
ANCOVAでは、部署による研修効果の違いを、研修前のスコアによる影響を調整した上で解釈するために、サマリや確率分布、多重比較などの情報があります。
サマリ
「サマリ」をクリックすると、各変数の有意性を確認することができます。
 この結果から、以下のことが分かります。
この結果から、以下のことが分かります。
- 研修前スコア(共変量)が研修後のスコアに大きな影響を与えていることが確認できます(F値 = 4770、P値が0に限りなく近い)。つまり、研修前スコアが研修後スコアを予測する上で非常に重要な要因であることを示しています。
- 部署単独の効果はP値が0.46(46%)のため、統計的に有意ではないことを示しています。
- 「部署 * 研修前スコア」の交互作用は、P値が0.51(51%)のため、統計的に有意ではないことを示しています。これは、研修前スコアの影響が部署によって大きく異なることはないことを示しています
この結果により、研修効果を予測する上で最も重要なのは研修前のスコアであり、部署の違いはあまり重要ではなく、研修前スコアの影響は全ての部署でほぼ同じように働いているといえます。
多重比較
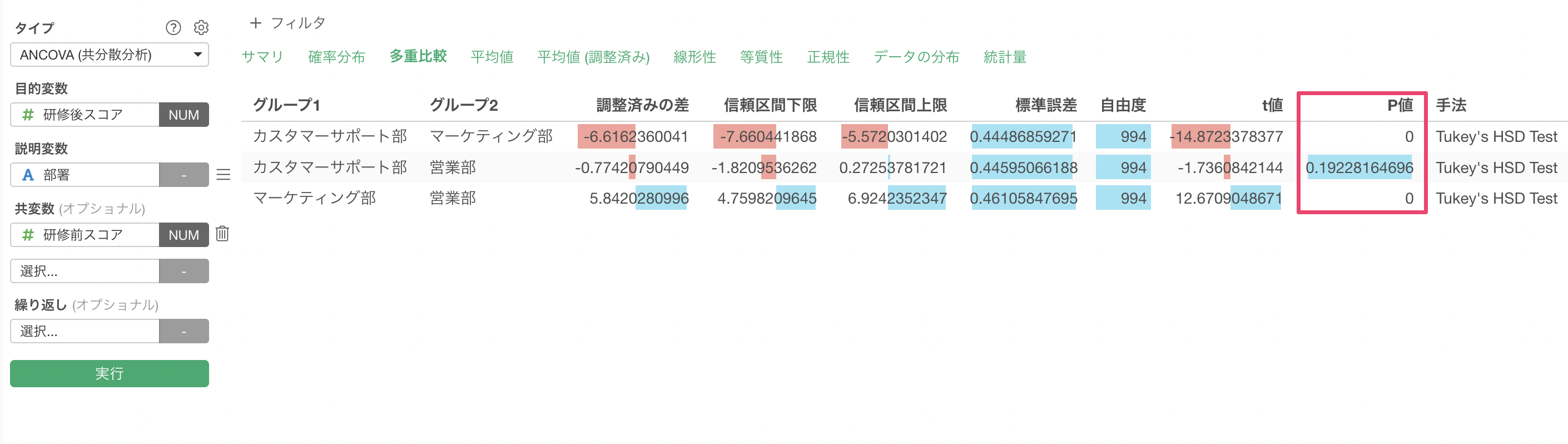
「多重比較」タブでは、Tukey’s HSD検定による部署間の平均値の差の検定結果を確認できます。
 分析結果から、以下のことが分かります。
分析結果から、以下のことが分かります。
カスタマーサポート部とマーケティング部、マーケティング部と営業部ではP値が限りなく0に近いため、統計的に有意であることが確認できます。一方で、カスタマーサポート部と営業部のP値は0.19(19%)と統計的な有意差は見られません。
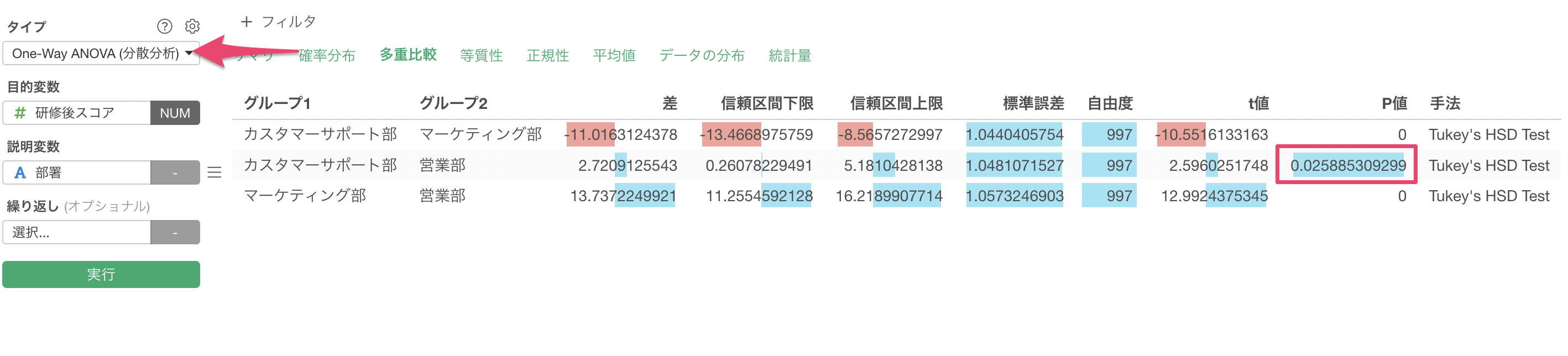
もしOne-Way Anova(分散分析)を実行した時には、カスタマーサポート部と営業部のP値は0.025(2.5%)と統計的な有意差があるように見えてしまいます。共分散分析では、研修前のスコアによる影響を調整をしているために、有意ではなくなっているようです。
平均値
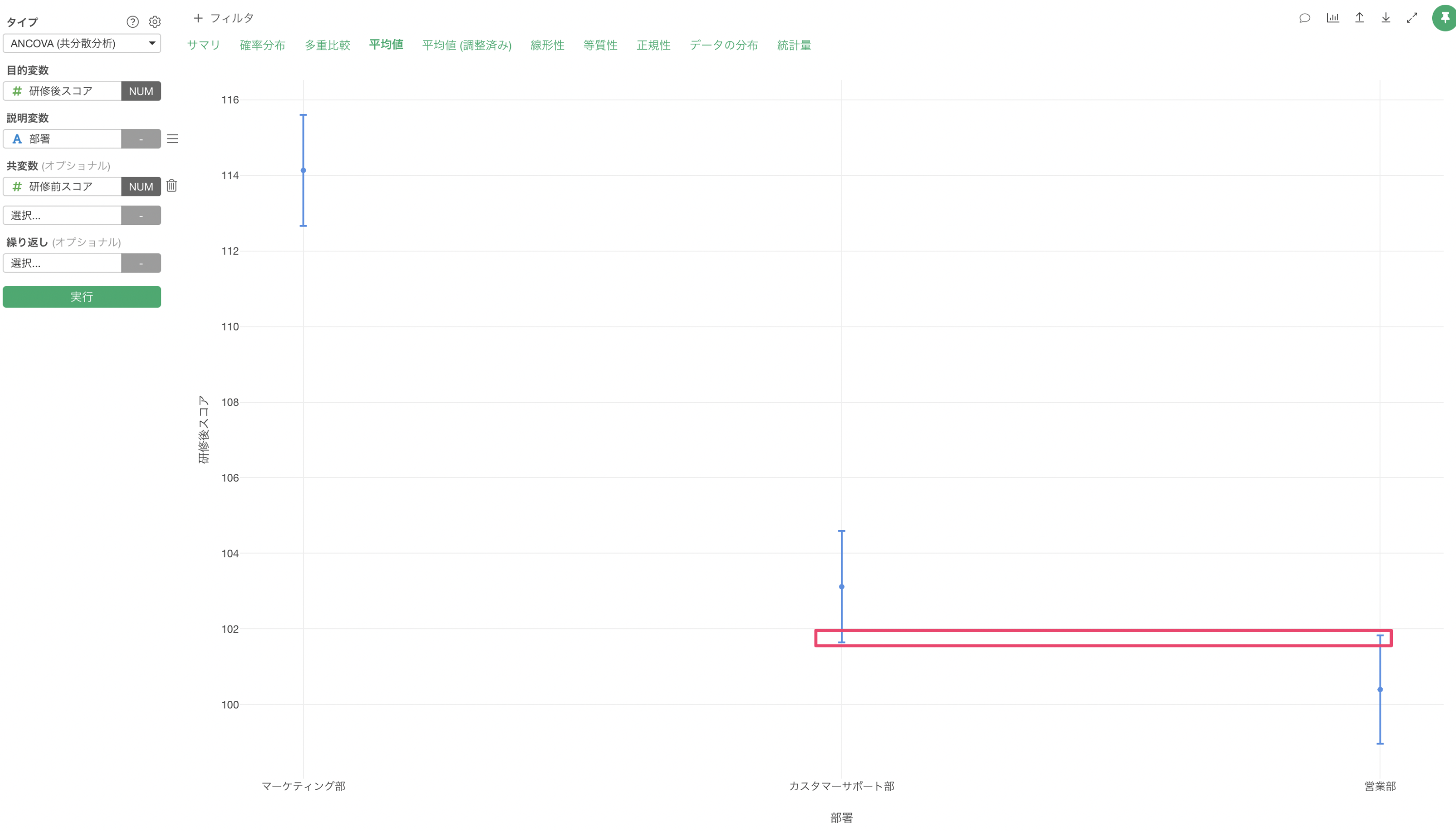
「平均値」タブでは、各部署の研修後スコアの実際の平均値を確認できます。
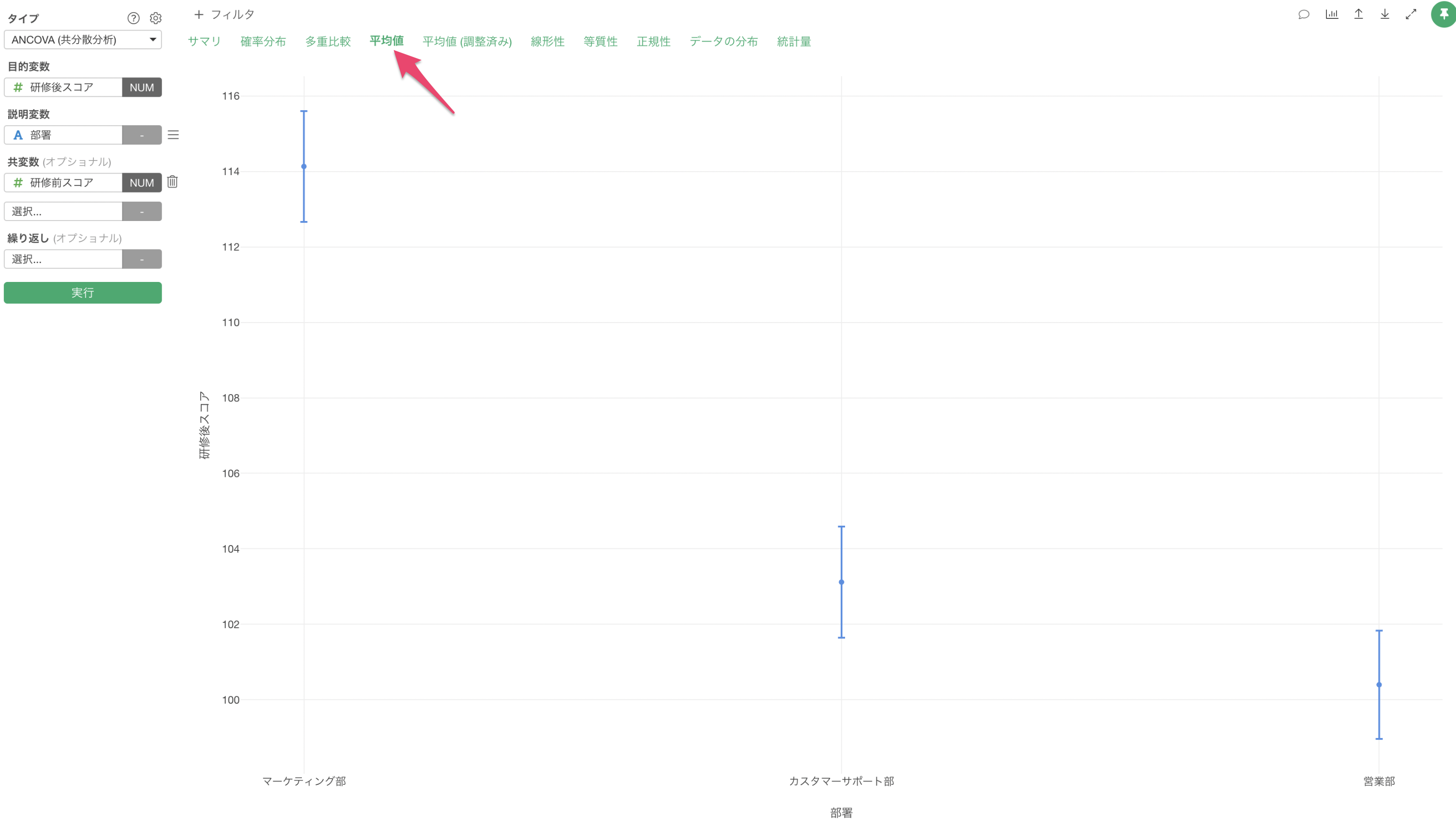
この結果を見ると、カスタマーサポート部と営業部の研修後スコアの平均値の信頼区間はあまり重なっていないため、統計的に有意かどうかを断定することはできませんが、先程紹介したOne-Way Anovaの結果ではP値が2.5%となっており、研修後スコアだけで部署の違いを見ると有意に見えてしまいます。
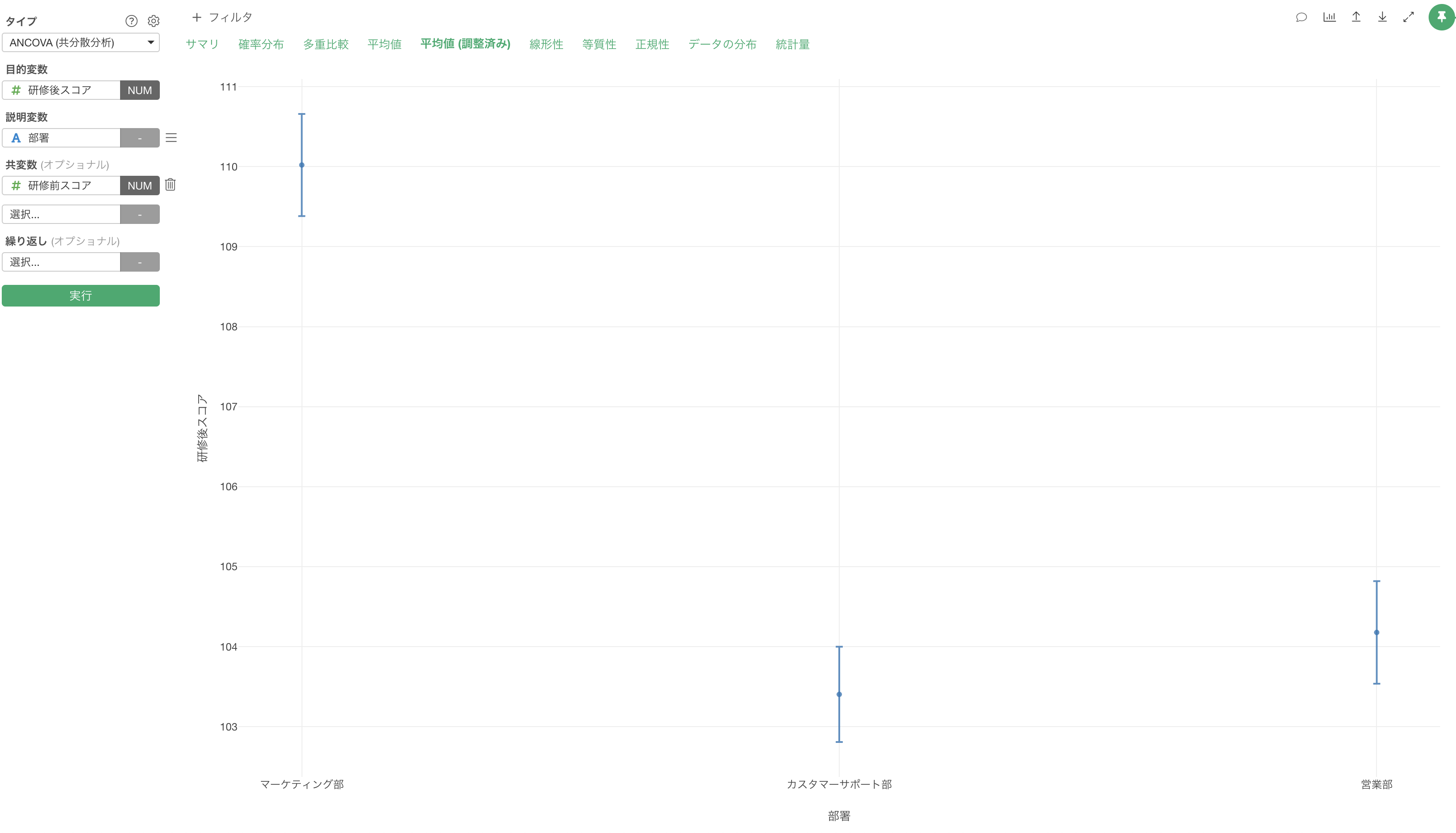
平均値 (調整済み)
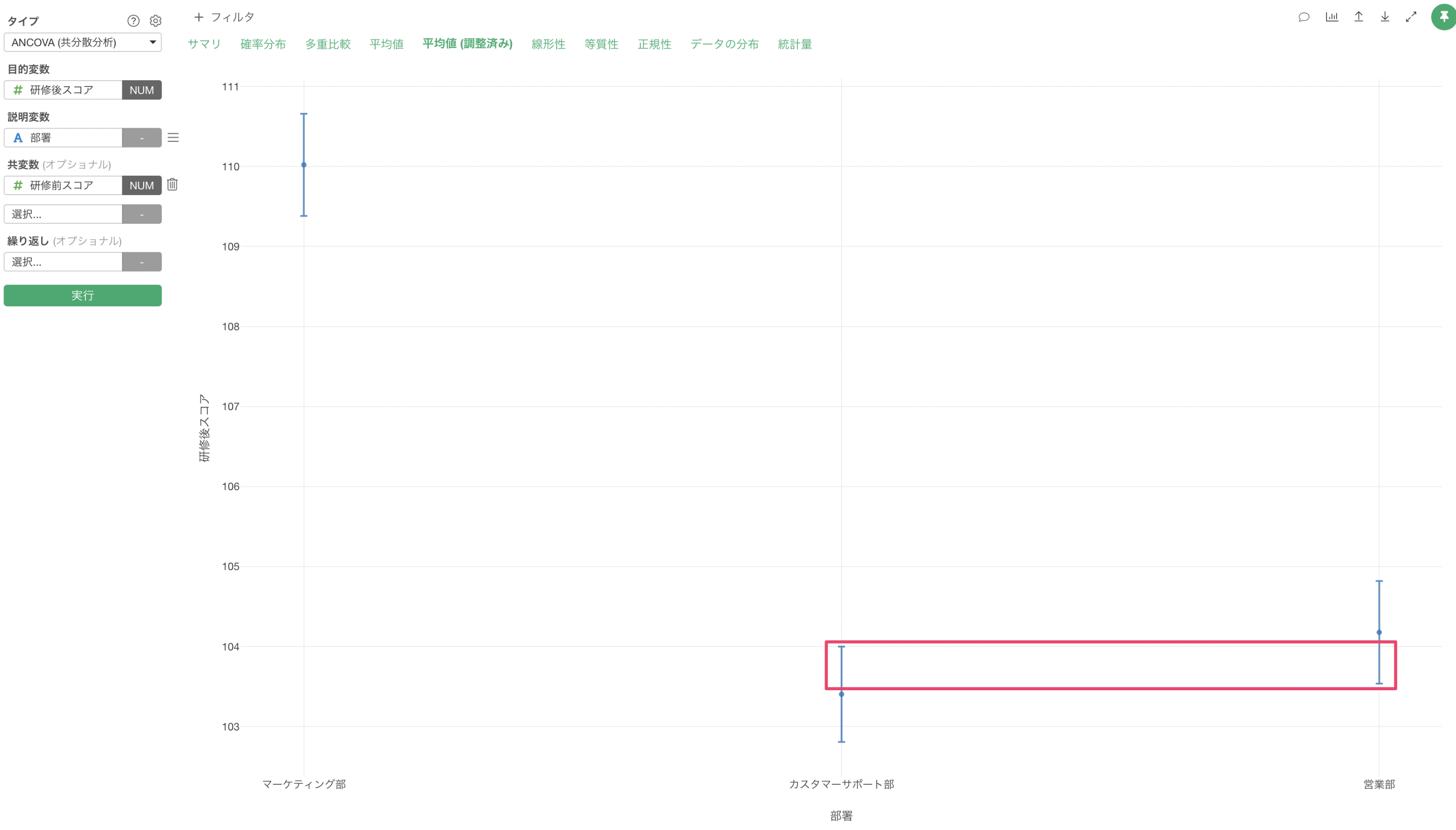
「平均値 (調整済み)」タブでは、研修前スコアの影響を調整した後の各部署の平均値を確認できます。
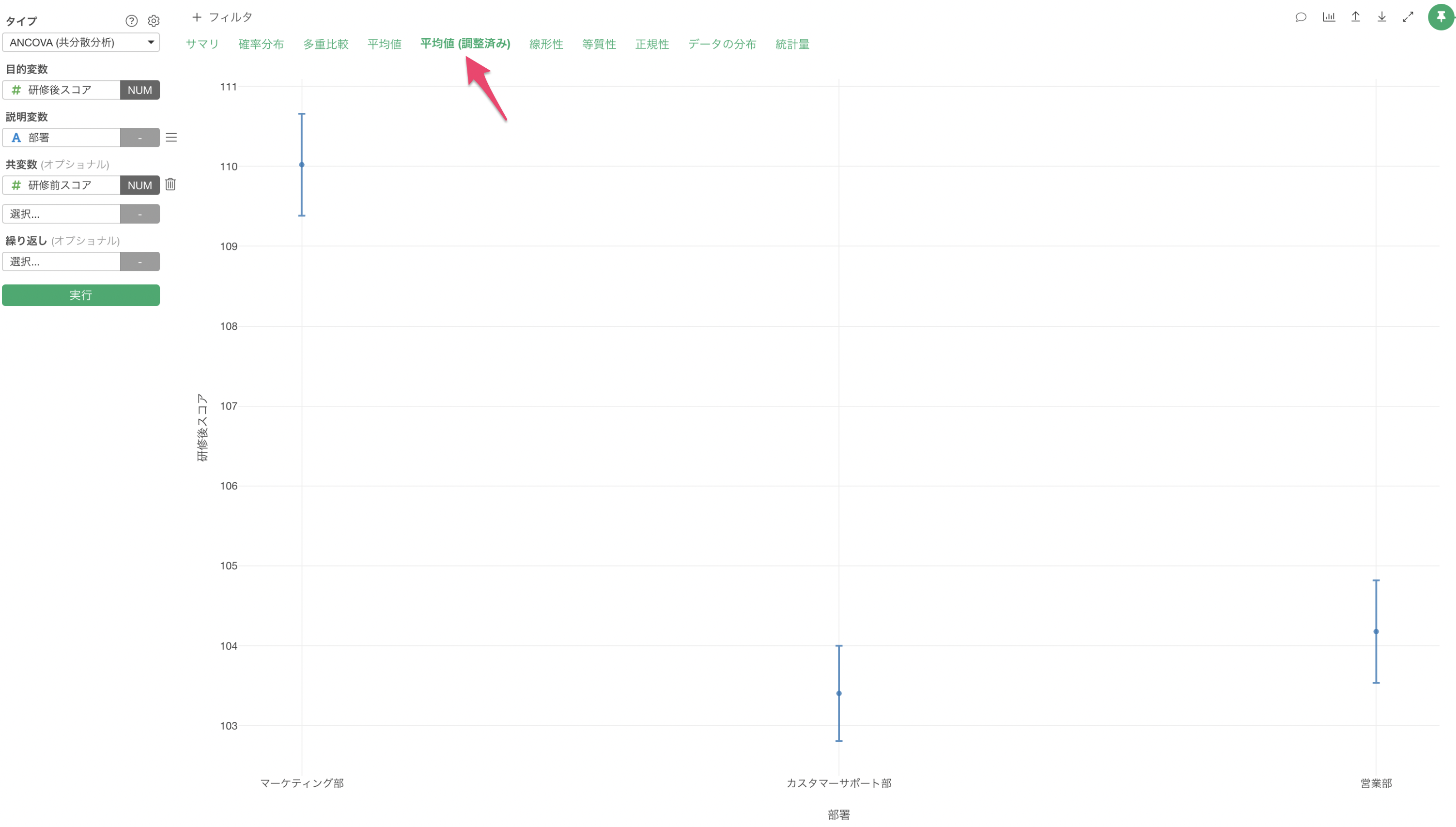
この結果から、研修前の能力差を考慮すると、実際の平均値で見られた部署間の差が小さくなっており、特にカスタマーサポート部と営業部の差は、研修前のスコアの影響を調整すると、ほとんど見られなくなることが示されています。
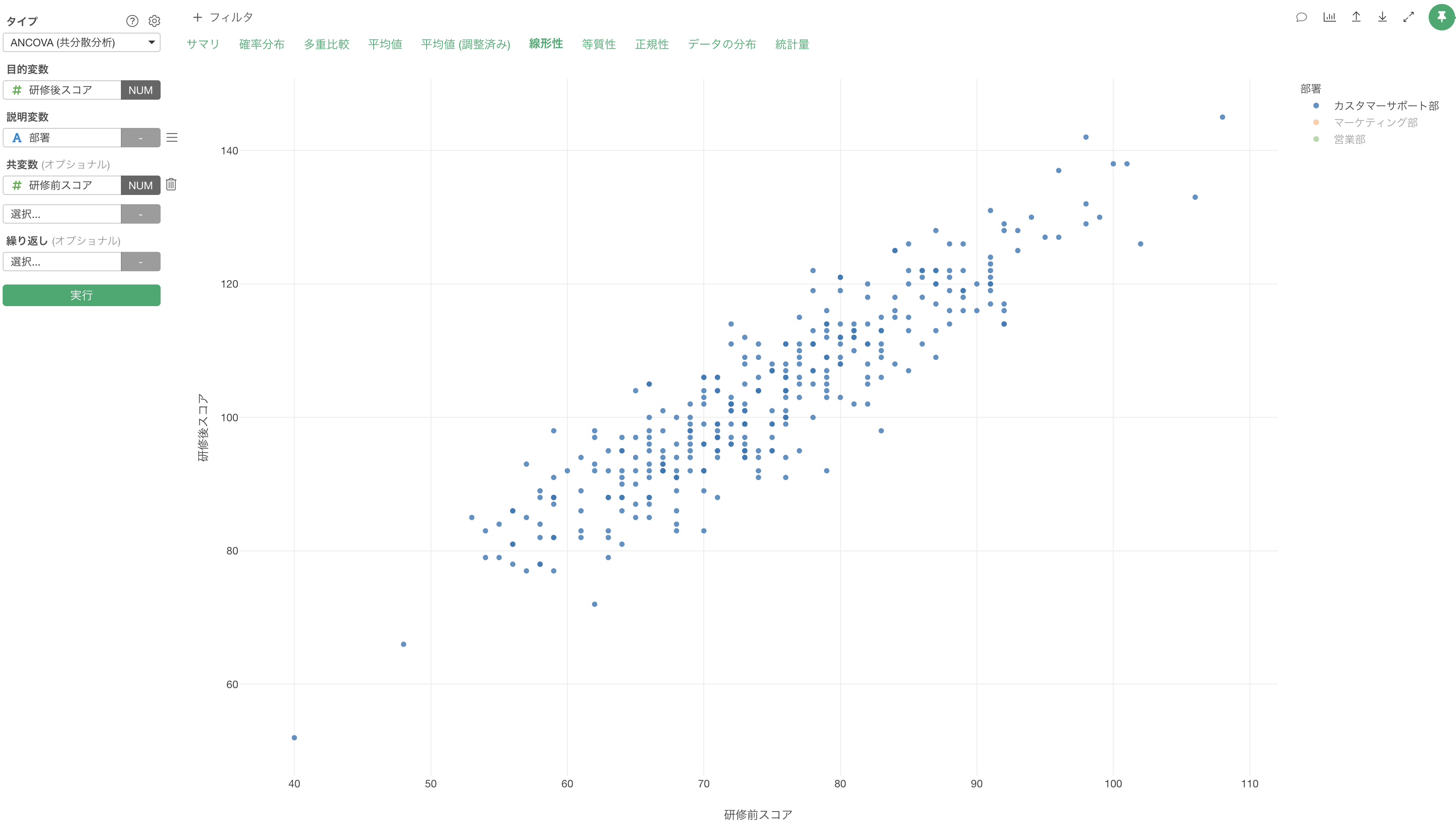
線形性
「線形性」タブでは、共変量(研修前スコア)と目的変数(研修後スコア)の関係が線形であるかを確認できます。
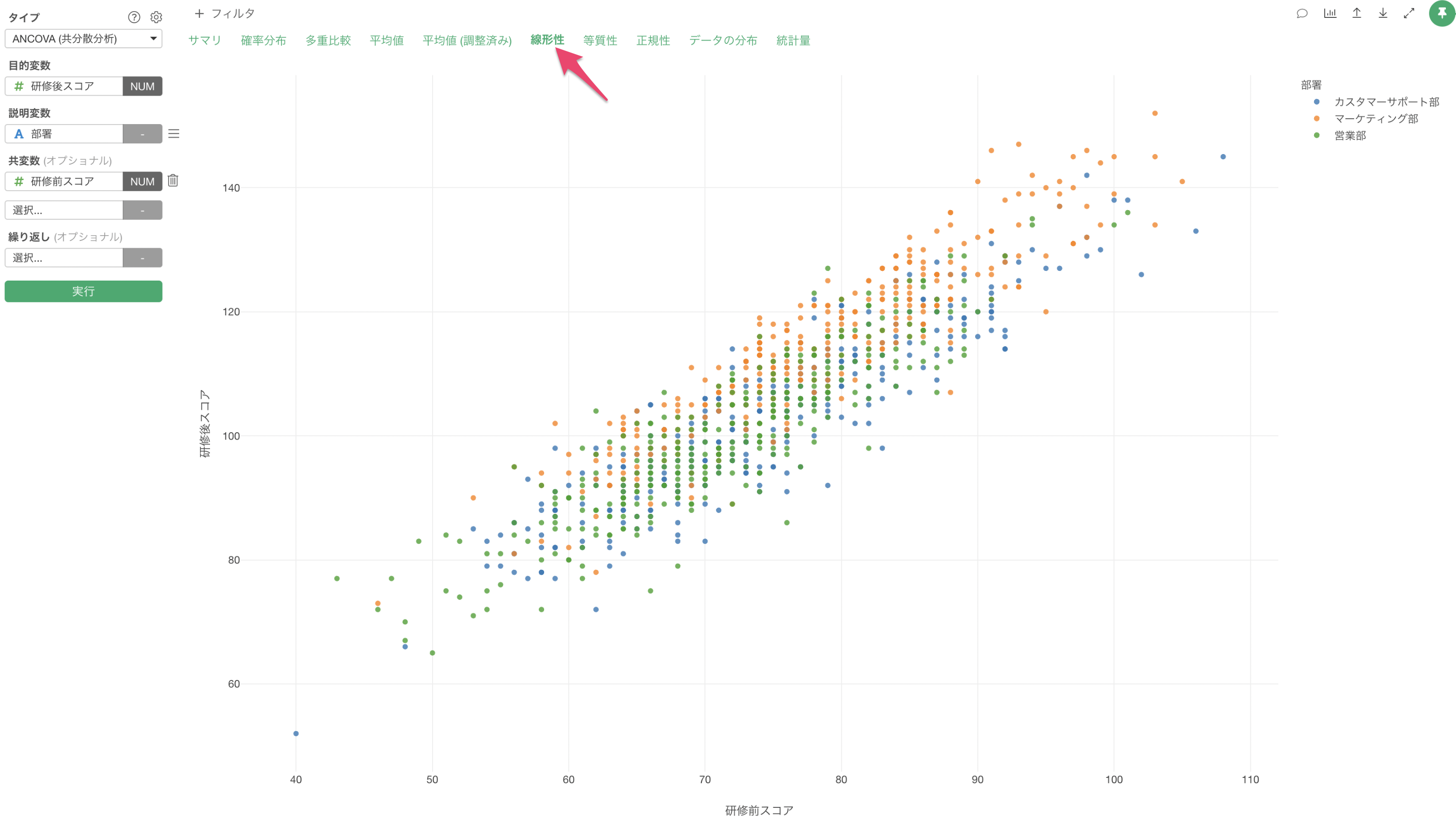
結果を見ると、研修前スコアと研修後スコアの間に明確な線形関係があるように確認できます。
等質性
「等質性」タブでは、「分散等等質性の前提が満たされているか」、「満たされていないか」を確認できます。

今回の結果から、研修前スコアと研修後スコアの関係性が類似しており、「分散の等質性の前提」が満たされていることが確認できます。

4. まとめ
ANCOVAは、グループ間の比較を行う際に、共変量の影響を考慮することができる強力な分析手法です。今回の事例では、研修前のスコアという共変量の影響を調整した上で、部署による研修効果の違いを評価することができました。この手法により、単純な平均値の比較では見えなかった「純粋な」効果の違いを把握することが可能となり、より正確な意思決定を行うことができます。
特に、教育効果の測定や医療における治療効果の比較、人材育成プログラムの評価など、初期状態の違いを考慮する必要がある場面で非常に有用な手法といえます。ただし、データが前提条件(線形性、等質性など)を満たしているかどうかの確認が重要となります。