
時系列予測 (ARIMA/SARIMA)の使い方
時系列予測(ARIMA/SARIMA)は、過去のデータパターンを基に将来の値を予測する統計手法です。ARIMA(自己回帰和分移動平均)モデルは、データの傾向(トレンド)を捉え、SARIMAはさらに季節性を考慮に入れることができます。この手法は、データに含まれる3つの重要な要素:自己回帰(AR)、和分(I)、移動平均(MA)を組み合わせることで、複雑な時系列パターンをモデル化します。特に、定期的な変動やトレンドを持つビジネスデータの分析に適しており、例えば売上予測や需要予測などで広く活用されています。
ARIMAモデルの特徴は、データの過去の値(自己回帰)と予測誤差(移動平均)の両方を考慮し、非定常なデータを定常化(和分)することで、より正確な予測を可能にする点です。さらに、SARIMAモデルでは季節性を加味することで、年間の売上変動や月次の需要サイクルなど、ビジネスでよく見られる周期的なパターンも効果的に予測することができます。これにより、在庫管理の最適化や人員配置の効率化など、より戦略的な意思決定をサポートすることが可能となります。
この分析手法の重要な特徴は、データの自己相関(時系列データの値同士の関連性)を詳細に分析し、最適なモデルパラメータを自動的に選択できる点です。また、予測結果には信頼区間が付与されるため、将来の不確実性も考慮した意思決定が可能となります。
1. どういった時に使えるのか
時系列予測(ARIMA/SARIMA)は、時間の経過とともに変化するデータを分析し、将来の傾向を予測したい場合に特に有効です。例えば、小売業では日々の売上データから将来の需要を予測し、適切な在庫管理や人員配置を行うために活用できます。また、製造業では生産量の予測に使用され、原材料の調達や生産計画の最適化に役立てることができます。特に、データに季節性(例:夏季の需要増加)やトレンド(例:年々の成長)が存在する場合、SARIMAモデルを使用することで、より精度の高い予測が可能となります。
この手法は、Web サービスのトラフィック予測にも効果的です。時間帯や曜日、季節による利用者数の変動パターンを分析し、サーバーリソースの最適な配分を計画することができます。さらに、エネルギーセクターでは、電力需要の予測に活用され、効率的な電力供給の計画立案に貢献しています。金融分野では、売上や収益の予測、さらには市場動向の分析にも応用されています。
なお、同じ時系列予測でも「Prophet」と比較すると、ARIMA/SARIMAは以下のような特徴や違いがあります:
- ARIMA/SARIMAは、データ間の自己相関関係を詳細にモデル化するため、短期的な変動パターンの予測に強みがあります。一方、Prophetは長期的なトレンドや大きな季節性パターンの予測に適しています。
- ARIMA/SARIMAは、データが等間隔で欠損値がない場合に最も効果を発揮します。Prophetは不規則なデータや欠損値がある場合でも扱いやすい特徴があります。
- ARIMA/SARIMAは、外部変数(天候や気温など)の影響を取り入れにくい一方で、Prophetは外部予測変数を容易にモデルに組み込むことができます。
- データ量が少ない場合(1年未満など)は、ARIMA/SARIMAの方が安定した予測を行える傾向にあります。
- モデルの専門性について:ARIMAは統計モデルのため、パラメーターの調整に専門知識を要することがありますが、ProphetはARIMAのような時系列予測のモデルと異なり、統計、時系列予測の専門知識がなくても使えるようにデザインされています。
Prophetについて興味がある方は、こちらをご覧ください。
時系列予測(ARIMA/SARIMA)は、以下のようなデータで特に効果を発揮します:
- 日次・週次・月次の売上データ
- 顧客訪問数や利用者数の推移データ
- エネルギー消費量の時系列データ
- 製品の需要量の推移データ
2. ユースケース
小売業での使い方
- 小売店舗では、日次の売上予測や商品カテゴリごとの需要予測に使用できます。
- 具体的には、過去の売上データと季節性、イベントの影響を考慮することで、より正確な将来の売上予測が可能となります。
- これにより、在庫の最適化、スタッフのシフト計画、販促施策の効果測定などを効率的に行うことができます。
製造業での使い方
- 製造業では、製品の需要予測や生産計画の最適化に活用できます。
- 具体的には、過去の生産量データと市場動向を分析することで、将来の需要量を予測し、適切な生産計画を立てることができます。
- これにより、原材料の効率的な調達や生産ラインの最適な稼働計画を立案することが可能となります。
需要予測担当者での使い方
- 需要予測担当者は、各商品カテゴリの将来需要を予測する際に活用できます。
- 具体的には、過去の需要パターンから季節性や傾向を分析し、より精度の高い需要予測を行うことができます。
- これにより、在庫切れや過剰在庫のリスクを最小限に抑えた発注計画を立てることが可能となります。
マーケティング担当者での使い方
- マーケティング担当者は、販促施策の効果予測や顧客行動の分析に活用できます。
- 具体的には、過去のキャンペーン効果や季節要因を考慮した売上予測を行い、最適なマーケティング施策を計画できます。
- これにより、効果的な予算配分や販促タイミングの決定を行うことが可能となります。
3. Exploratoryで時系列予測 (ARIMA/SARIMA)を実行する
使用するデータ
今回は「小売店舗売上データ」を使用します。データはこちらからダウンロードが可能となっています。

このデータは小売店舗の売上情報を記録したもので、1行が1日分のデータとなっており、列には「日付」「売上金額」などのデータがあります。
時系列予測(ARIMA/SARIMA)を作るためには、以下のようなデータの構造が必要となります。
- 時系列を表す日付/時間の列が必要です。
- 予測対象となる数値列(今回は売り上げ金額)が必要です。
- 日付/時間は等間隔である必要があります(欠損値がないこと)
アナリティクスを作成する
小売店舗売上データから「アナリティクス・ビュー」を開きます。

タイプに「時系列分析」を選び、「時系列予測 (ARIMA/SARIMA)」を選択します。

日付/時間には「日付」の列を選び、日付単位には「日」を選択します。値には「売上金額」の列を割り当てます。

最後に、「実行」ボタンをクリックして実行結果を確認します。

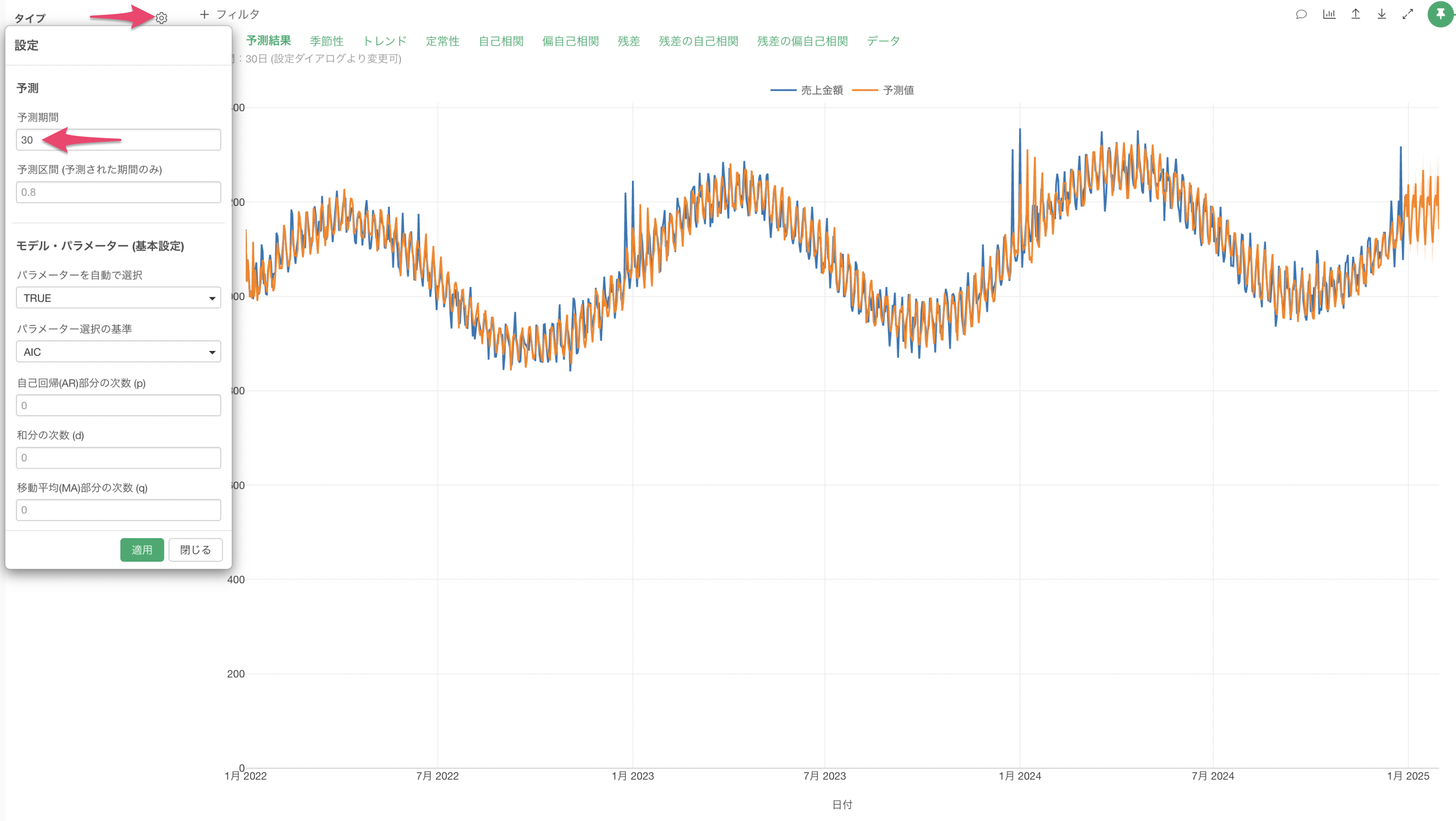
実行をすると、予測期間はデフォルトでは10区間分となり、今回は日付の単位が「日」のため、10日後までの予測となっています。

ARIMAでは長期な予測にはあまり向いていないこともあるため、今回は予測期間には「30」を指定して、30日後までの結果を予測します。
結果の解釈
サマリ
「サマリ」をクリックすると、モデルの予測精度の指標を確認することができます。

予測モデルの精度を示す主な数値は以下の通りです。

- 予測の平均的な誤差(RMSE): 29.22
- 予測のズレの平均(MAE): 21.91
- 予測の誤差率(MAPE): 2.02%(誤差が約2%という意味)
- データの当てはまり具合(R²): 0.93(1に近いほど良い)
これらの数値から、このモデルは高い精度で予測できていることがわかります。特に誤差率が2%程度と小さく、信頼できる予測といえます。
予測結果
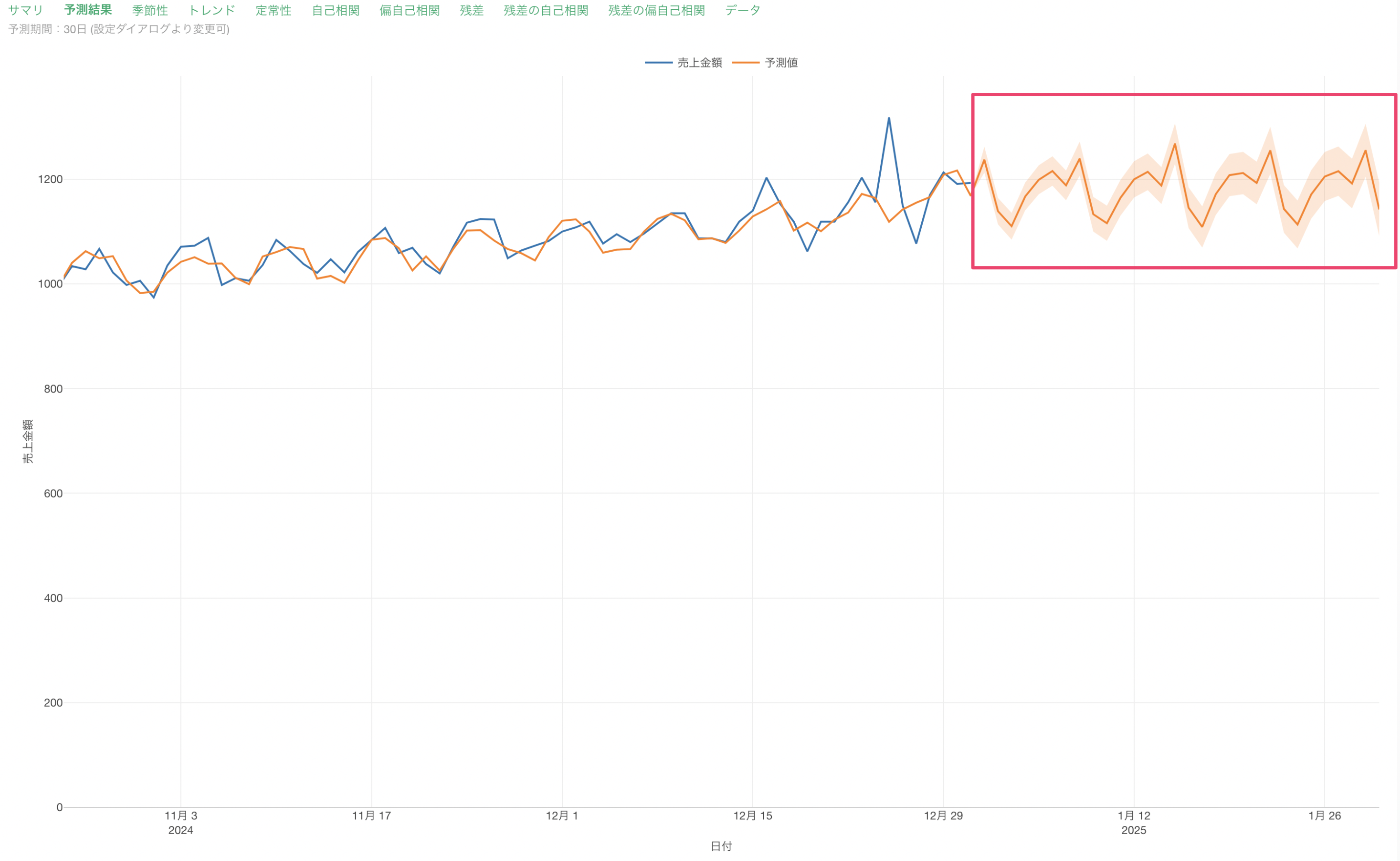
「予測結果」をクリックすると、実測値(青い線)、そして予測値(オレンジの線)とその予測区間を確認することができます。

この結果から、ARIMAのモデルの予測値は実際の売上金額の動きを捉えていることがわかります。

一方で、将来の予測(30日間)で見た時には、それぞれの週での売上金額は同じパターンが繰り返されているため、突発的な変化は予測できないことが考えられます。
季節性
「季節性」をクリックすると、データに含まれる周期的なパターンを確認することができます。

より細かく周期性を確認するために、チャートでドラッグ&ドロップをして範囲を拡大します。

今回は日単位での予測のため、1週間単位で繰り返される売上パターンを示しており、毎週日曜日と月曜日の売上金額は高いが、木曜日と金曜日は低いといった傾向が確認できます。

トレンド
「トレンド」をクリックすると、長期的な変動傾向を確認することができます。
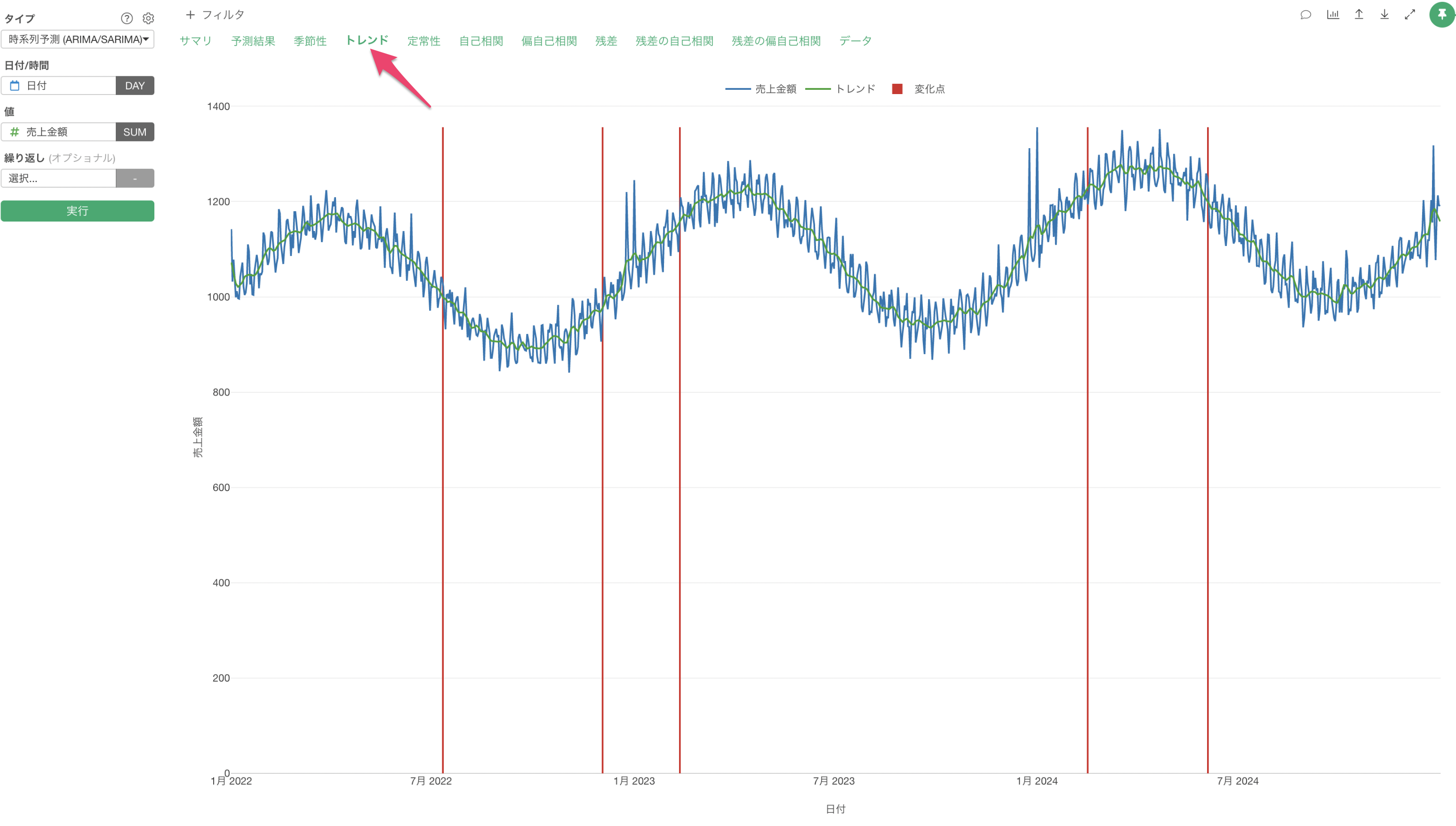
売上の長期的な傾向を見ると、緩やかな成長トレンドが確認できます。季節による変動も明確で、7-8月の夏場に売上が低下し、年末年始に向けて上昇する傾向があります。また、2-3月には緩やかな低下が見られます。赤い縦線で示される変化点は主に季節の変わり目で発生していることがわかります。

定常性
「定常性」をクリックすると、データの定常性に関する統計的な検定結果を確認することができます。

KPSS検定(Kwiatkowski-Phillips-Schmidt-Shin検定)は、時系列データが安定しているか(定常性があるか)を確認するための統計的な検定方法で、このグラフはKPSS検定による残差分析の結果を示しています。
売上金額の残差(実際の値とモデルの予測値との差)を見ると、0を中心として上下にばらついており、±50程度の範囲内で変動していることがわかります。ただし、2023年1月や2024年1月付近では±150を超える大きな外れ値も観察されます。これらの大きな残差は、年始のような特殊な期間での予測が難しいことを示唆しています。

しかし、全体としては残差の変動幅が比較的安定しており、明確な増加・減少トレンドは見られません。これは、モデルが基本的なデータの特性をよく捉えていることを示しています。
自己相関
「自己相関」をクリックすると、時系列データの自己相関関数(ACF)を確認することができます。

自己相関とは、時系列データにおいて、現在の値と過去の値との関係の強さを示すものです。グラフの横軸は「ラグ」と呼ばれ、何日前のデータとの関係を見ているかを表します。縦軸は相関係数で、-1から1の間の値をとり、0に近いほど関係が弱く、±1に近いほど関係が強いことを示します。
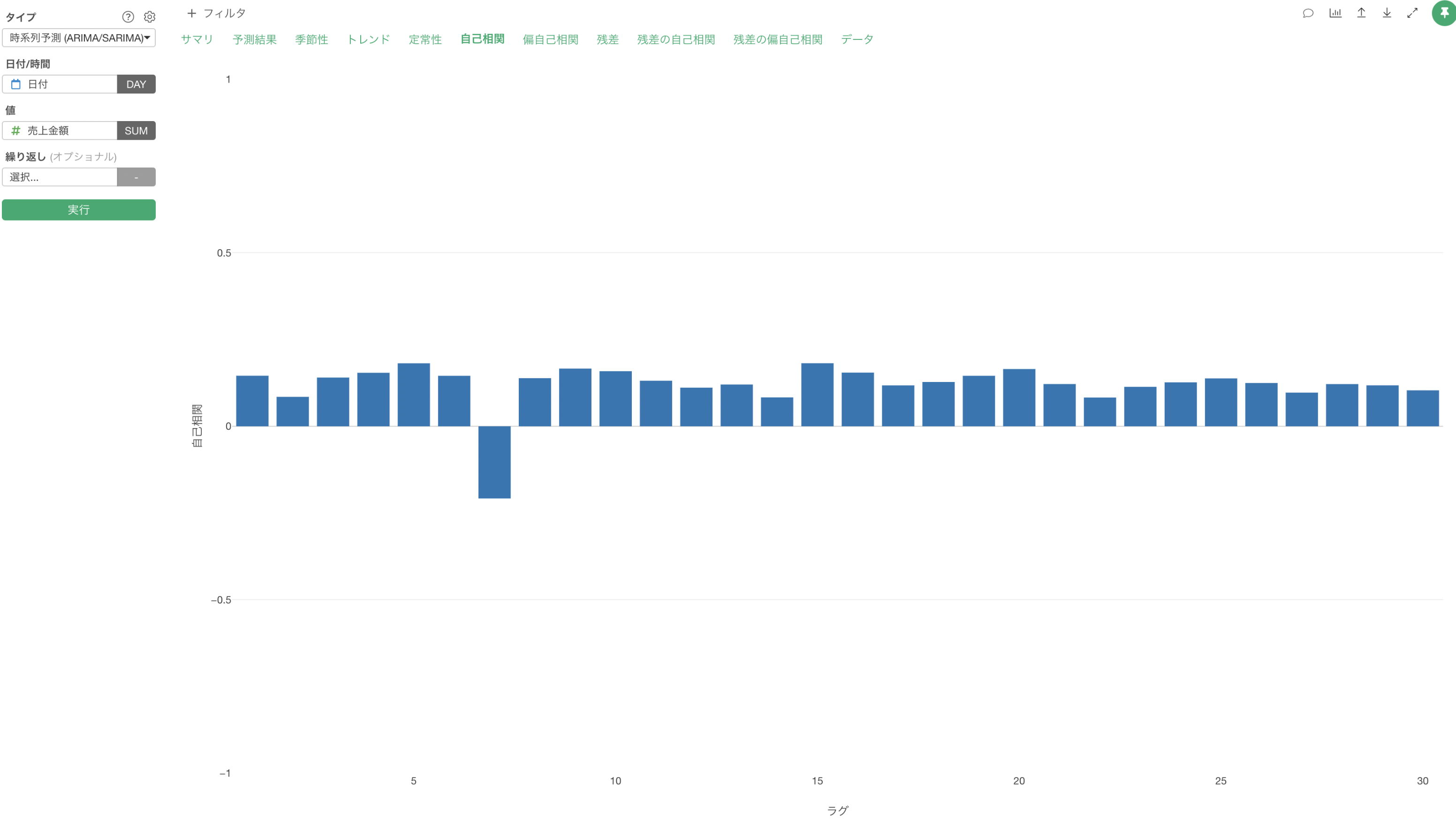
時系列データの自己相関分析の結果を見ると、全体的に相関係数は小さな値を示しています。最も顕著な値でも7日前との相関が-0.21程度であり、これは弱い負の相関を示すに過ぎません。その他のラグについては、さらに相関係数が小さく、ほとんどが±0.2未満の範囲に収まっています。
このことから、過去の売上と現在の売上との間には、強い関連性は見られないことがわかります。
偏自己相関
「偏自己相関」をクリックすると、時系列データの偏自己相関関数(PACF)を確認することができます。

偏自己相関とは、時系列データにおいて、間にある値の影響を除外した上で、現在の値と過去の値との直接的な関係の強さを示すものです。グラフの横軸は「ラグ」と呼ばれ、何日前のデータとの直接的な関係を見ているかを表します。縦軸は偏相関係数で、自己相関と同様に-1から1の間の値をとり、0に近いほど直接的な関係が弱く、±1に近いほど直接的な関係が強いことを示します。

偏自己相関分析の結果を見ると、全体的に偏相関係数は小さな値を示しています。最も顕著な値でも7日前との偏相関が-0.3程度であり、これは弱い直接的な負の関係性を示すに過ぎません。その他のラグについては、さらに偏相関係数が小さく、ほとんどが±0.2未満の範囲に収まっています。
適度な自己相関や偏自己相関(+0.3 ~ +0.7 )があることで、過去のデータを利用して将来を予測することができる可能性が高くなるため、ARIMAを使う場合には自己相関があるデータの方が精度が高くなりやすいです。
4. まとめ
時系列予測(ARIMA/SARIMA)は、過去のデータパターンから将来の予測を行う統計手法です。特に、トレンドや季節性を持つビジネスデータの分析に適しており、短期的な売上予測や需要予測などで幅広く活用できます。