Exploratoryでステップワイズ法を使って変数の自動選択を行う方法

ステップワイズ法は、統計的な基準（主にAIC）に基づいて、変数を自動的に追加または削除し、最適な変数の組み合わせを探索する手法です。

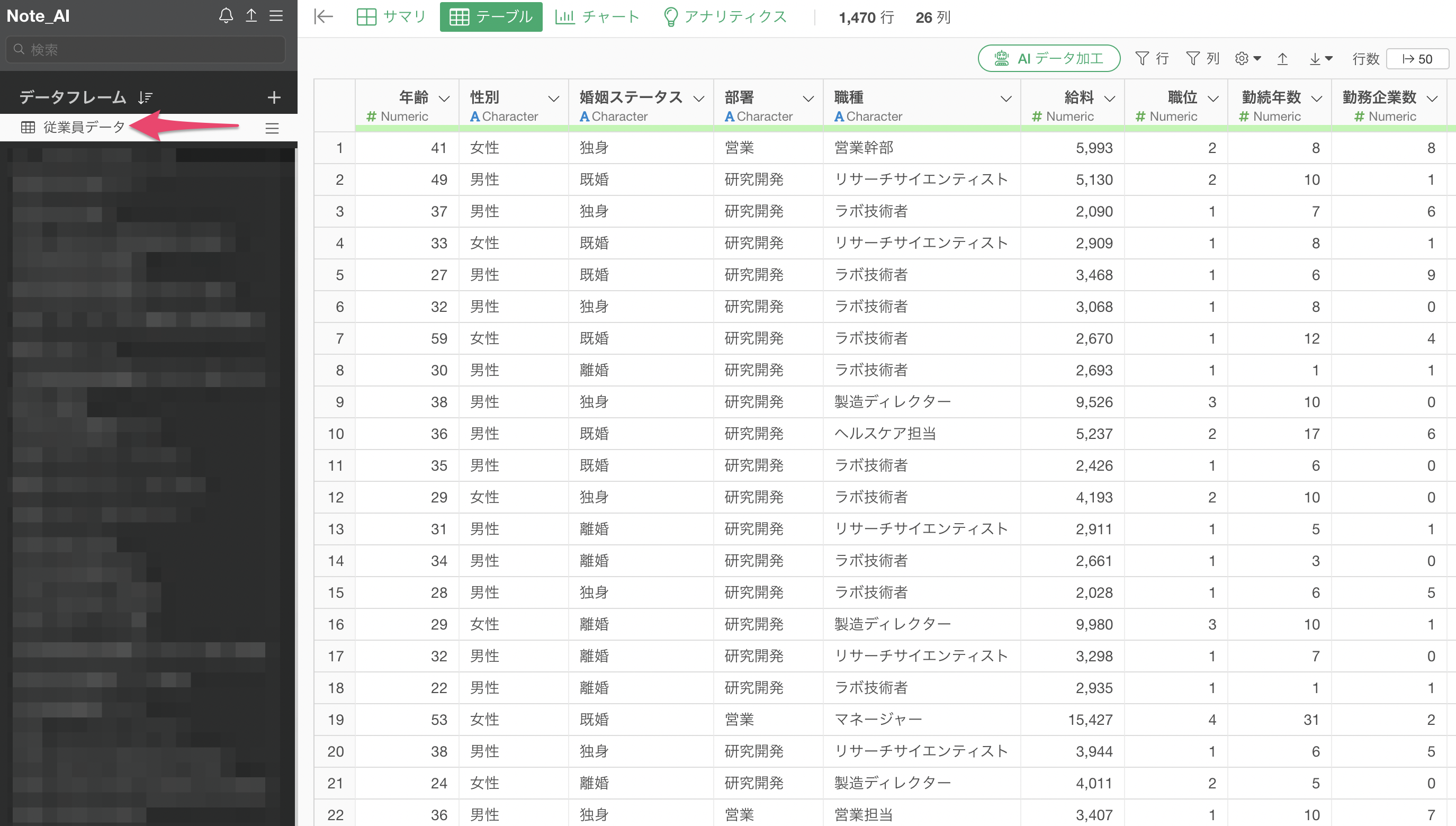
予測モデルの精度を高めるために「どの変数（特徴量）を使うか」を決定する際に有用ですし。Exploratoryの標準の機能では、ステップワイズ法はサポートされていないため、「ノート」機能にてRパッケージであるMASSを使うことで、ステップワイズ法による変数選択を実行できます。

ステップワイズ法の詳細

ステップワイズ法には主に3つのアプローチがあります。今回使用するRスクリプトは「両方向（Both）」を採用しています。

前向き選択 (Forward Selection): 何もない状態から、最も予測に寄与する変数を1つずつ追加していく
後退削除 (Backward Elimination): 全ての変数を入れた状態から、不要な変数を1つずつ削除していく
両方向 (Stepwise / Both): 変数の追加と削除を組み合わせ、AIC（赤池情報量基準）が最小になるモデルを探す

必要なパッケージのインストール

まず、ステップワイズ法を実行するためのパッケージをインストールします。

プロジェクトメニューから「Rパッケージの管理」を選択します。

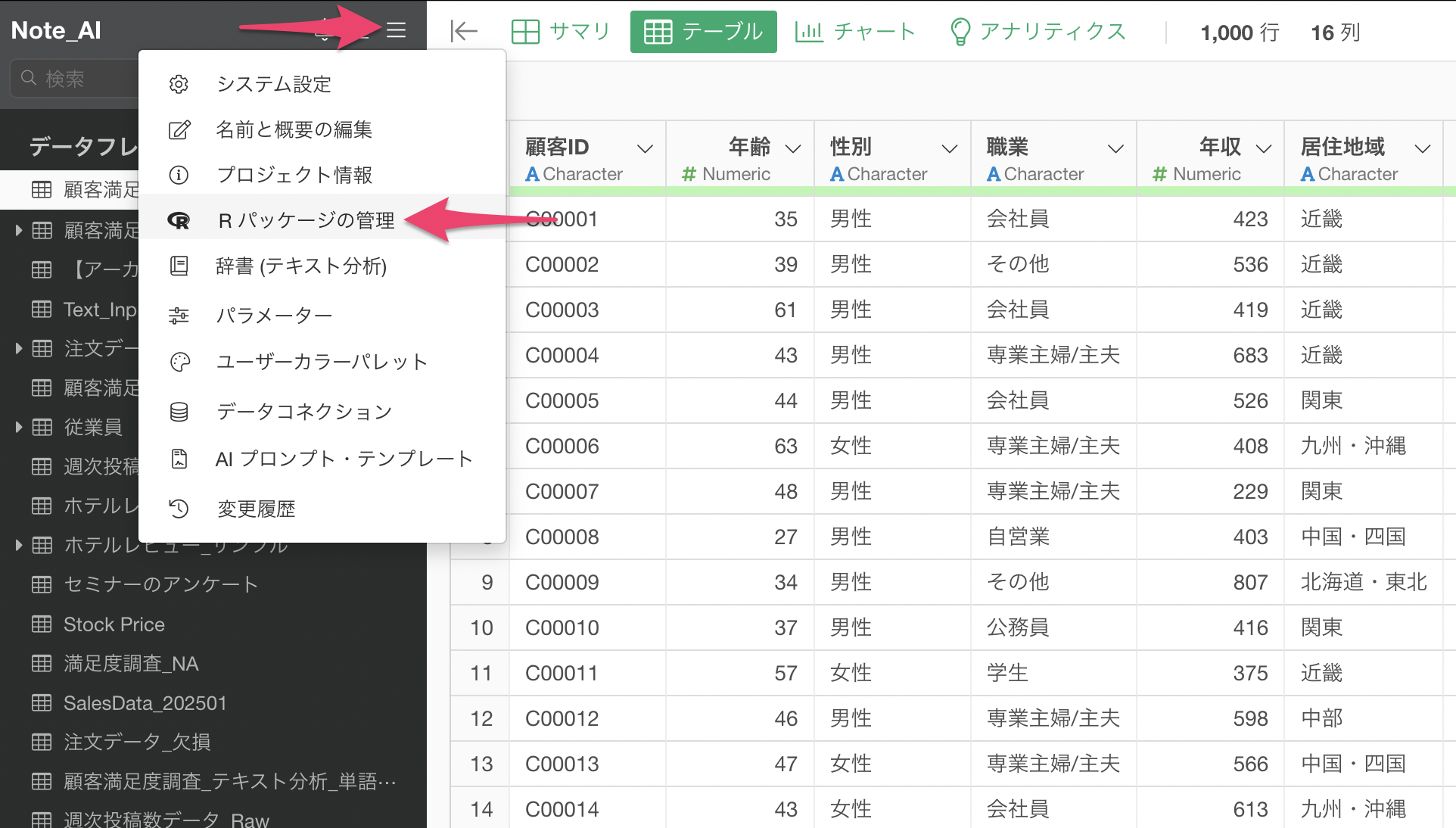
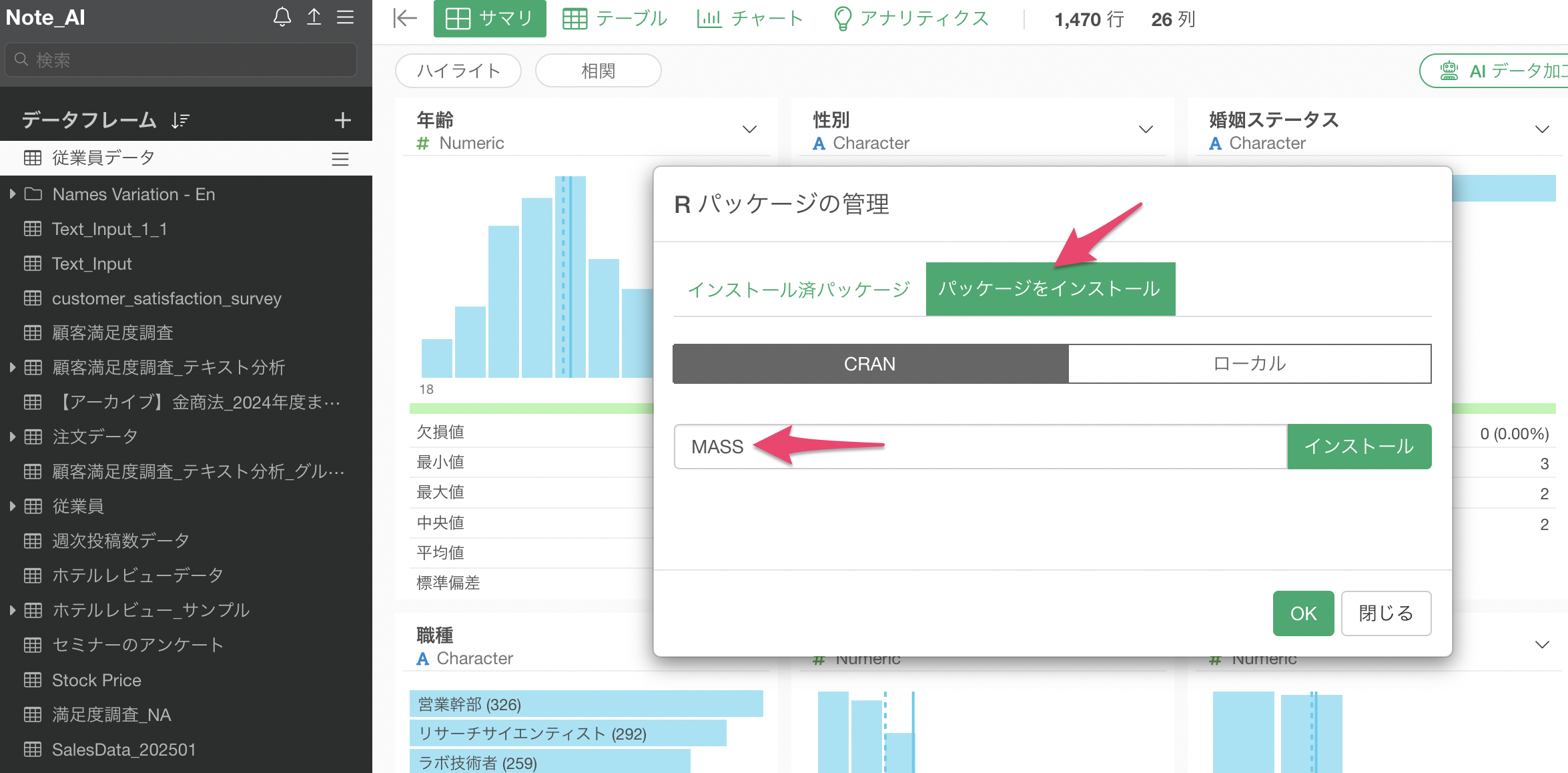
Rパッケージの管理のダイアログが表示されるため、パッケージをインストールをクリックしてから「MASS」パッケージをインストールしてください。

サンプルデータ

サンプルデータとして従業員データを使用します。データはこちらからダウンロードしていただけます。

ノートの作成

レポートのプラスボタンから「ノートを作成」を選択します。

ノートのウィンドウが開けたら、左上のプラスボタンから「Rコード」ボタンをクリックします。

Rスクリプトを記述するためのコードブロックが追加されました。

ステップワイズ法の実行

以下のRスクリプトを使用します。

library(MASS) # stepAIC関数のため

# データセットの読み込み
data(従業員データ)

# 最大モデル（全変数を含むモデル）の定義
full.model <- lm(給料 ~ ., data = 従業員データ)

# 最小モデル（インターセプトのみのモデル）の定義
null.model <- lm(給料 ~ 1, data = 従業員データ)

# ステップワイズ法によるモデル選択（前向き選択、後退削除、両方向選択が可能）
# direction = “both” は両方向選択（前向き選択と後退削除の組み合わせ）
step.model <- stepAIC(null.model, scope = list(lower = null.model, upper = full.model), direction = “both”, trace = 0)

# 最適なモデルの要約
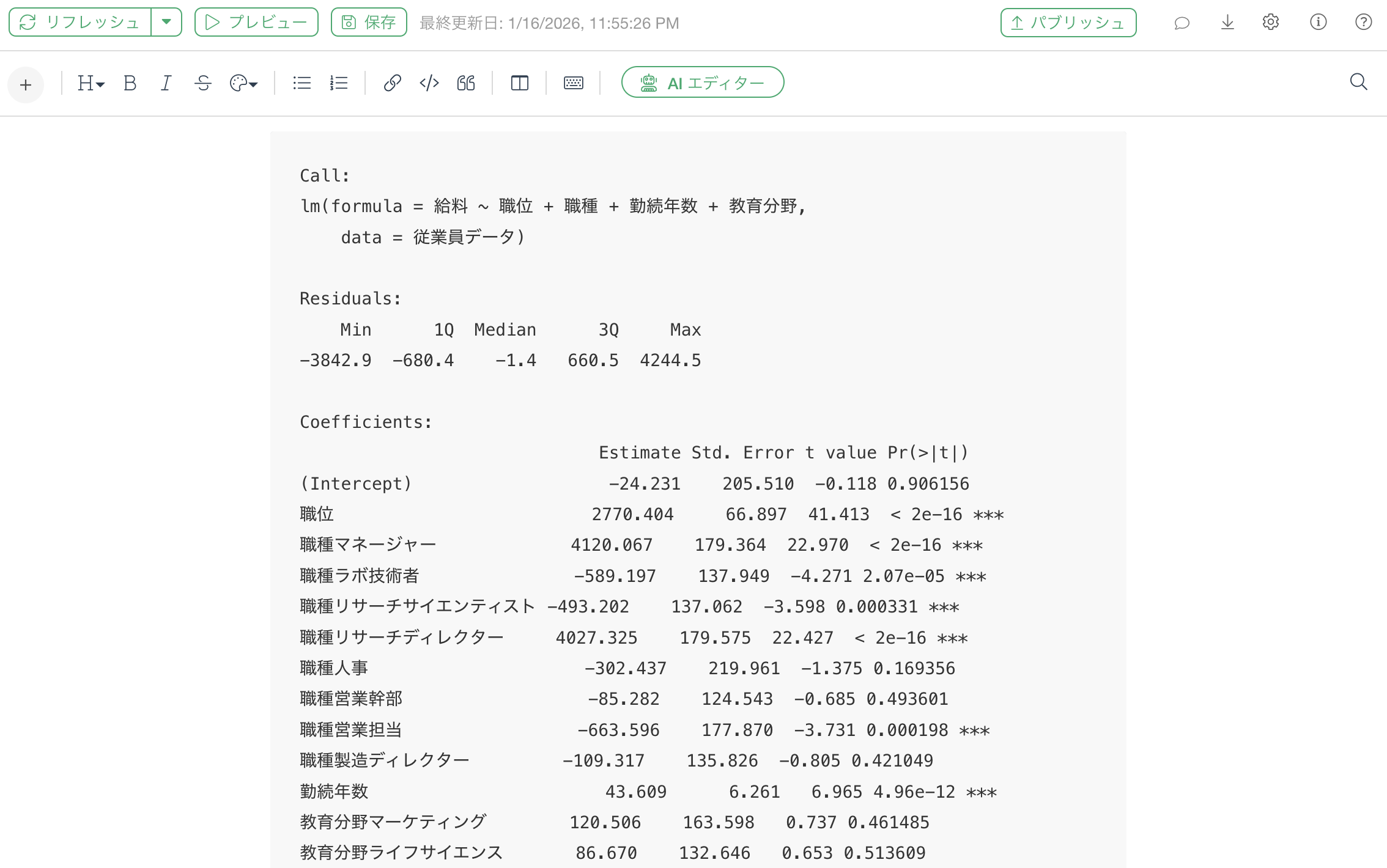
summary(step.model)

このRスクリプトを実行すると、最終的に選ばれたモデルのサマリー（係数、P値、決定係数など）が表示されます。


Call:
lm(formula = 給料 ~ 職位 + 職種 + 勤続年数 + 教育分野, 
    data = 従業員データ)

Residuals:
    Min      1Q  Median      3Q     Max 
-3842.9  -680.4    -1.4   660.5  4244.5 

Coefficients:
                             Estimate Std. Error t value Pr(>|t|)    
(Intercept)                   -24.231    205.510  -0.118 0.906156    
職位                         2770.404     66.897  41.413  < 2e-16 ***
職種マネージャー             4120.067    179.364  22.970  < 2e-16 ***
職種ラボ技術者               -589.197    137.949  -4.271 2.07e-05 ***
職種リサーチサイエンティスト -493.202    137.062  -3.598 0.000331 ***
職種リサーチディレクター     4027.325    179.575  22.427  < 2e-16 ***
職種人事                     -302.437    219.961  -1.375 0.169356    
職種営業幹部                  -85.282    124.543  -0.685 0.493601    
職種営業担当                 -663.596    177.870  -3.731 0.000198 ***
職種製造ディレクター         -109.317    135.826  -0.805 0.421049    
勤続年数                       43.609      6.261   6.965 4.96e-12 ***
教育分野マーケティング        120.506    163.598   0.737 0.461485    
教育分野ライフサイエンス       86.670    132.646   0.653 0.513609    
教育分野人事                  128.264    288.996   0.444 0.657235    
教育分野医療                   80.312    135.095   0.594 0.552278    
教育分野技術系                171.836    158.894   1.081 0.279677    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1125 on 1454 degrees of freedom
Multiple R-squared:  0.9435,    Adjusted R-squared:  0.9429 
F-statistic:  1618 on 15 and 1454 DF,  p-value: < 2.2e-16

自分のデータで分析する場合の変更箇所

上記のサンプルコードを自分のデータに適用する際は、以下の箇所を変更してください。

1. データフレーム名の指定

変更箇所: lm()関数のdataパラメータ

# 例：データフレーム名が「従業員データ」の場合

full.model <- lm(給料 ~ ., data = 従業員データ)
null.model <- lm(給料 ~ 1, data = 従業員データ)

# 例：データフレーム名が「売上データ」の場合

full.model <- lm(売上 ~ ., data = 売上データ)
null.model <- lm(売上 ~ 1, data = 売上データ)

2. 目的変数名の指定

変更箇所: lm()関数の式の左辺（チルダ~の左側）

# 例：目的変数が「給料」の場合

full.model <- lm(給料 ~ ., data = 従業員データ)
null.model <- lm(給料 ~ 1, data = 従業員データ)

# 例：目的変数が「売上」の場合

full.model <- lm(売上 ~ ., data = 売上データ)
null.model <- lm(売上 ~ 1, data = 売上データ)

3. 出力の詳細度の調整

変更箇所: stepAIC()関数のtraceパラメータ

# 選択過程を詳細に表示

trace = 1

# 選択過程を表示しない（結果のみ）

trace = 0

結果の読み方

ステップワイズ法を実行した summary()の結果には以下の情報が含まれます。

Call:
lm(formula = 給料 ~ 職位 + 職種 + 勤続年数 + 教育分野, 
    data = 従業員データ)

Residuals:
    Min      1Q  Median      3Q     Max 
-3842.9  -680.4    -1.4   660.5  4244.5 

Coefficients:
                             Estimate Std. Error t value Pr(>|t|)    
(Intercept)                   -24.231    205.510  -0.118 0.906156    
職位                         2770.404     66.897  41.413  < 2e-16 ***
職種マネージャー             4120.067    179.364  22.970  < 2e-16 ***
職種ラボ技術者               -589.197    137.949  -4.271 2.07e-05 ***
職種リサーチサイエンティスト -493.202    137.062  -3.598 0.000331 ***
職種リサーチディレクター     4027.325    179.575  22.427  < 2e-16 ***
職種人事                     -302.437    219.961  -1.375 0.169356    
職種営業幹部                  -85.282    124.543  -0.685 0.493601    
職種営業担当                 -663.596    177.870  -3.731 0.000198 ***
職種製造ディレクター         -109.317    135.826  -0.805 0.421049    
勤続年数                       43.609      6.261   6.965 4.96e-12 ***
教育分野マーケティング        120.506    163.598   0.737 0.461485    
教育分野ライフサイエンス       86.670    132.646   0.653 0.513609    
教育分野人事                  128.264    288.996   0.444 0.657235    
教育分野医療                   80.312    135.095   0.594 0.552278    
教育分野技術系                171.836    158.894   1.081 0.279677    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1125 on 1454 degrees of freedom
Multiple R-squared:  0.9435,    Adjusted R-squared:  0.9429 
F-statistic:  1618 on 15 and 1454 DF,  p-value: < 2.2e-16

このCall: lm(formula = 給料 ~ 職位 + 職種 + 勤続年数 + 教育分野, data = 従業員データ) の部分がステップワイズ法を使ってAIC（赤池情報量基準）が最小になる最適な変数だと言えます。

よくあるエラーと対処法

Error in library(MASS) : there is no package called ‘MASS’

原因: MASSパッケージがインストールされていない
対処: 「必要なパッケージのインストール」セクションの手順に従って、パッケージをインストールしてください

Error: object ‘従業員データ’ not found

原因: 指定した名前のデータフレームが存在しない、または綴りが間違っている
対処: プロジェクト内のデータフレーム名とスクリプト内の名前が完全に一致しているか確認してください

まとめ

ステップワイズ法は、統計的な基準（AIC）に基づいて予測モデルに含める変数を自動的に選択する手法です。ExploratoryのUIには直接的なステップワイズ法のメニューはありませんが、ノート機能でRのMASSパッケージを使用することで実行が可能です。

この方法により、Exploratory上で最適な変数選択を自動的に行うことが可能です。