生存曲線(カプランマイヤー法) - 打ち切りとは何か
カプランマイヤー法とは?
カプランマイヤー法は、生存時間を分析する統計手法の一つです。患者の治療効果や商品の故障率、サブスクリプションサービスの解約率など、「どれくらいの期間、ある状態が続くか」を調べるときに使われます。
この手法の最大の特徴は、「打ち切り」というデータの欠損を適切に処理できることです。つまり、すべての対象者について最終的な結果(死亡、故障、解約など)が確認できなくても、分析を行うことができます。
カプランマイヤー法の基本的な考え方
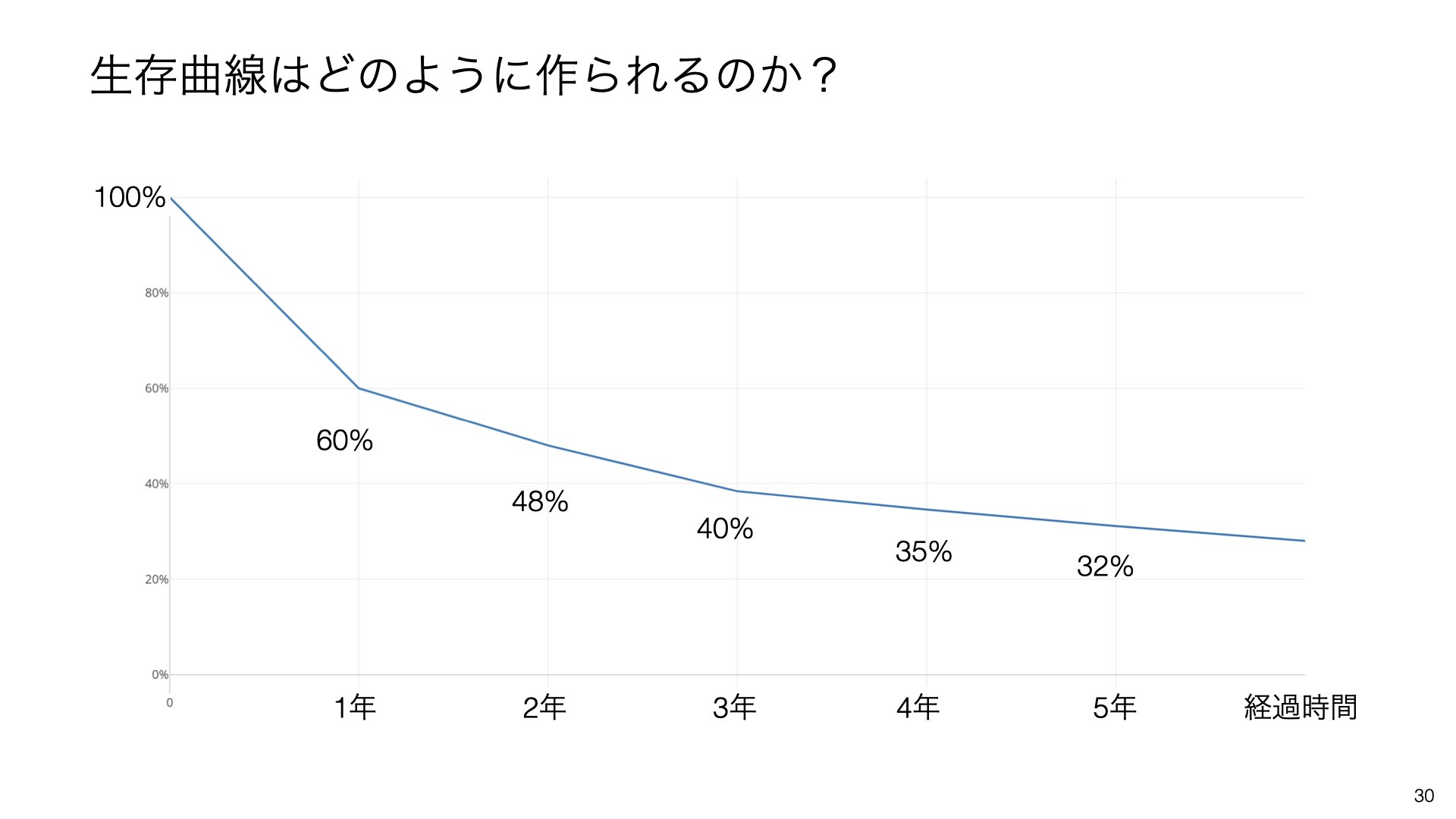
まず、生存曲線がどのように作られるかを理解しましょう。生存曲線は時間の経過とともに生存率(継続率)がどのように変化するかを表したグラフです。最初は100%から始まり、時間が経つにつれて徐々に減少していきます。
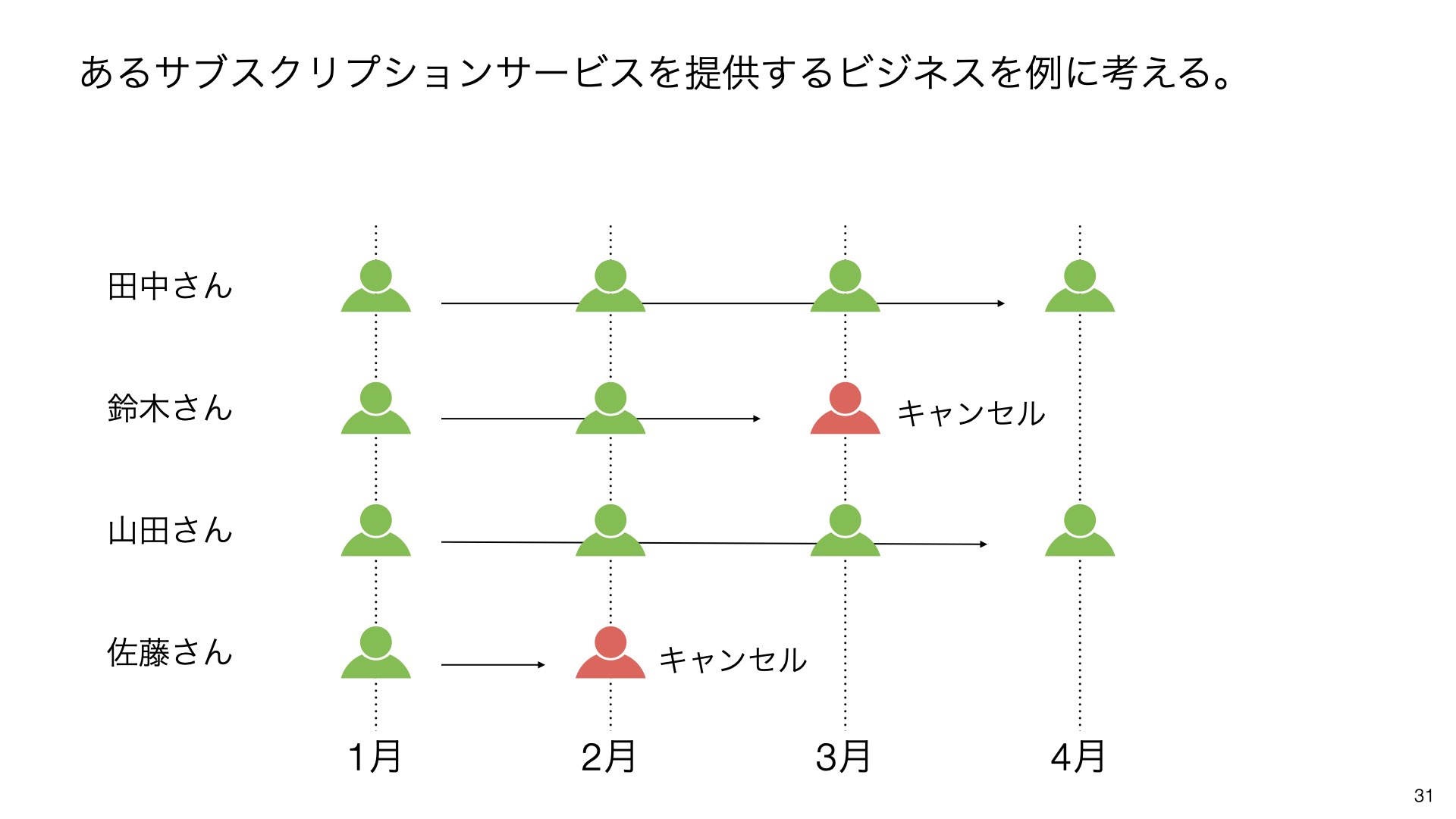
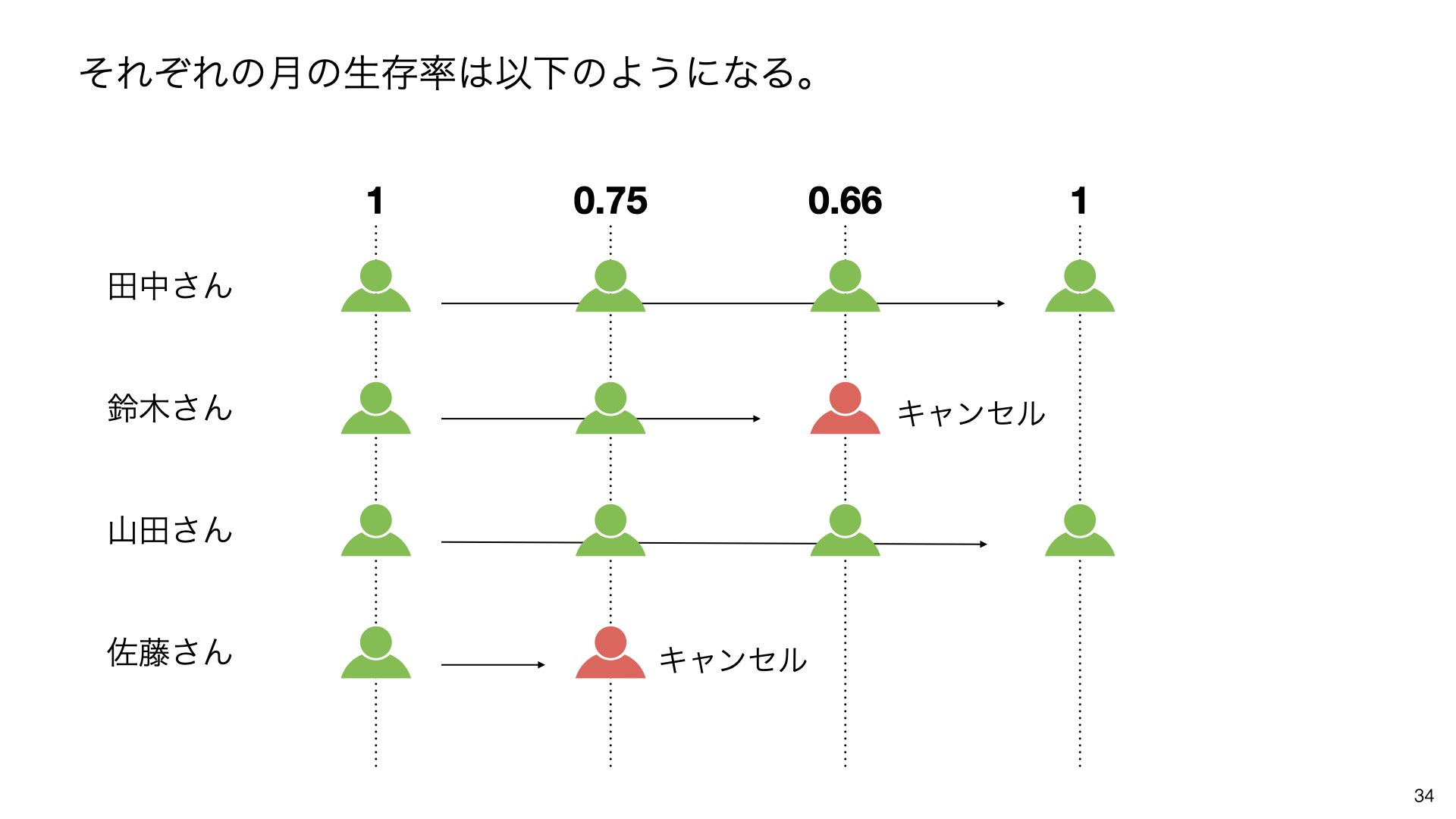
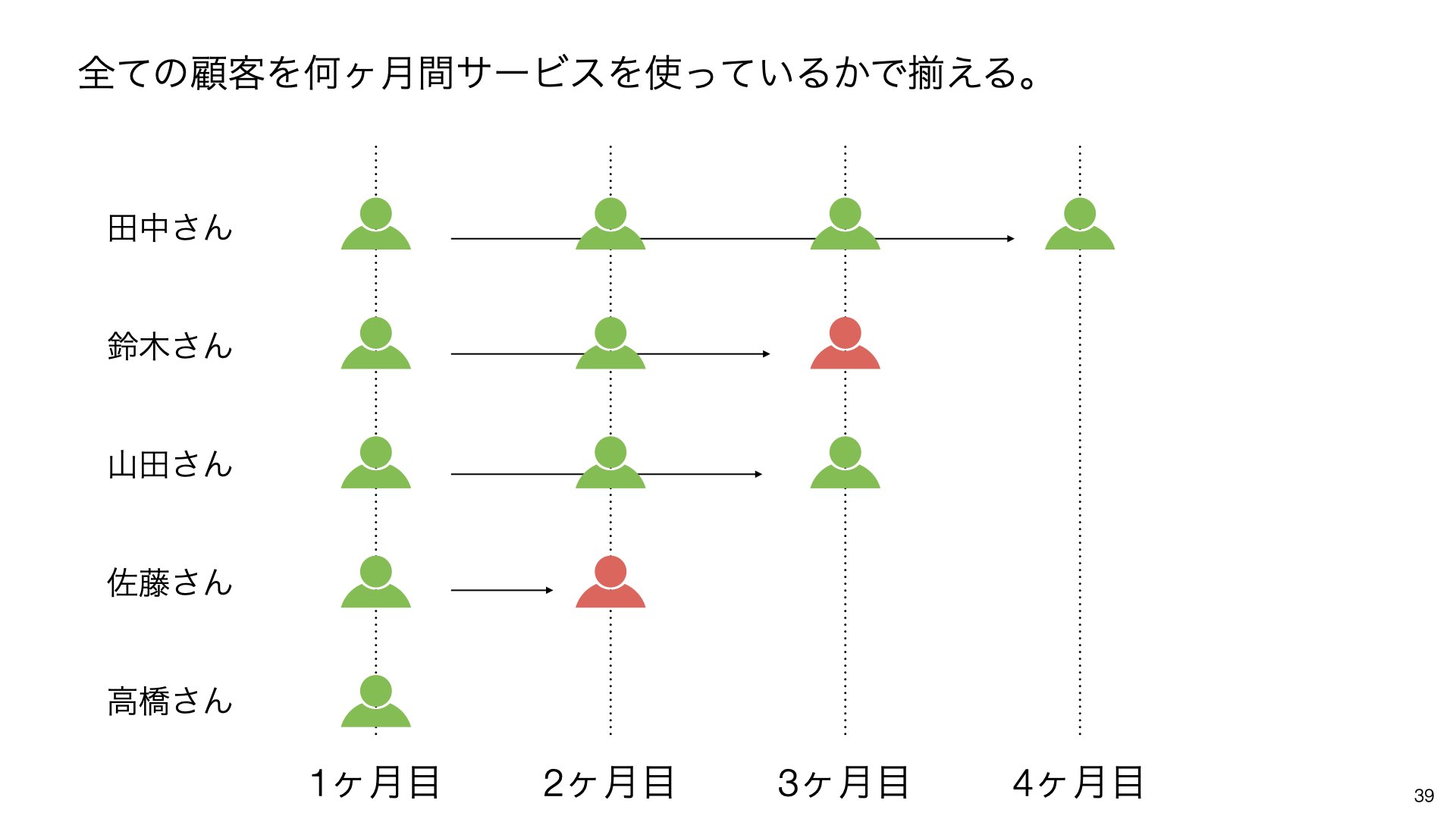
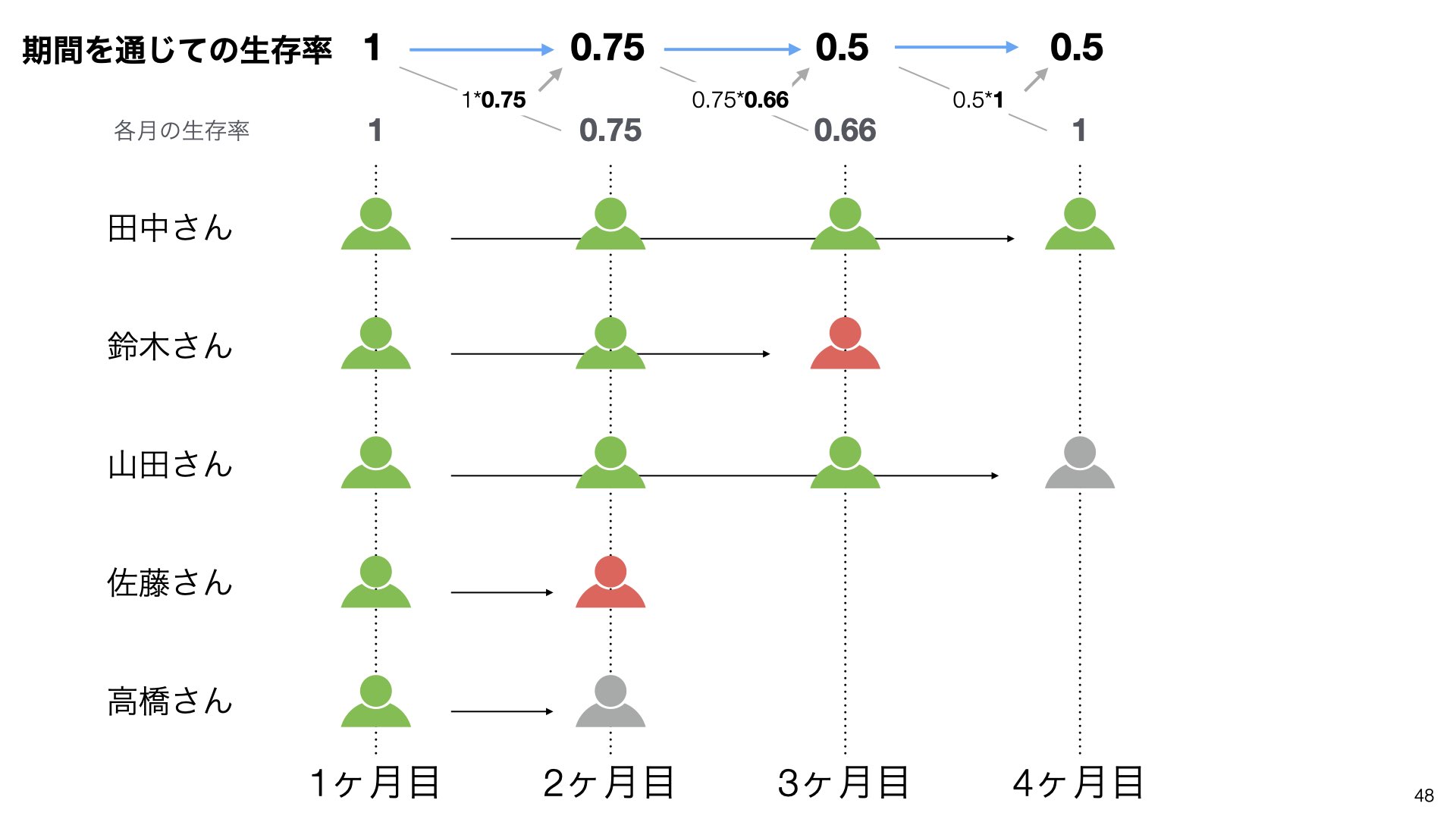
次に、具体的な例としてサブスクリプションサービスを考えてみましょう。5人の顧客(田中さん、鈴木さん、山田さん、佐藤さん、高橋さん)のサービス利用状況を追跡します。各顧客の継続状況を時系列で観察します。
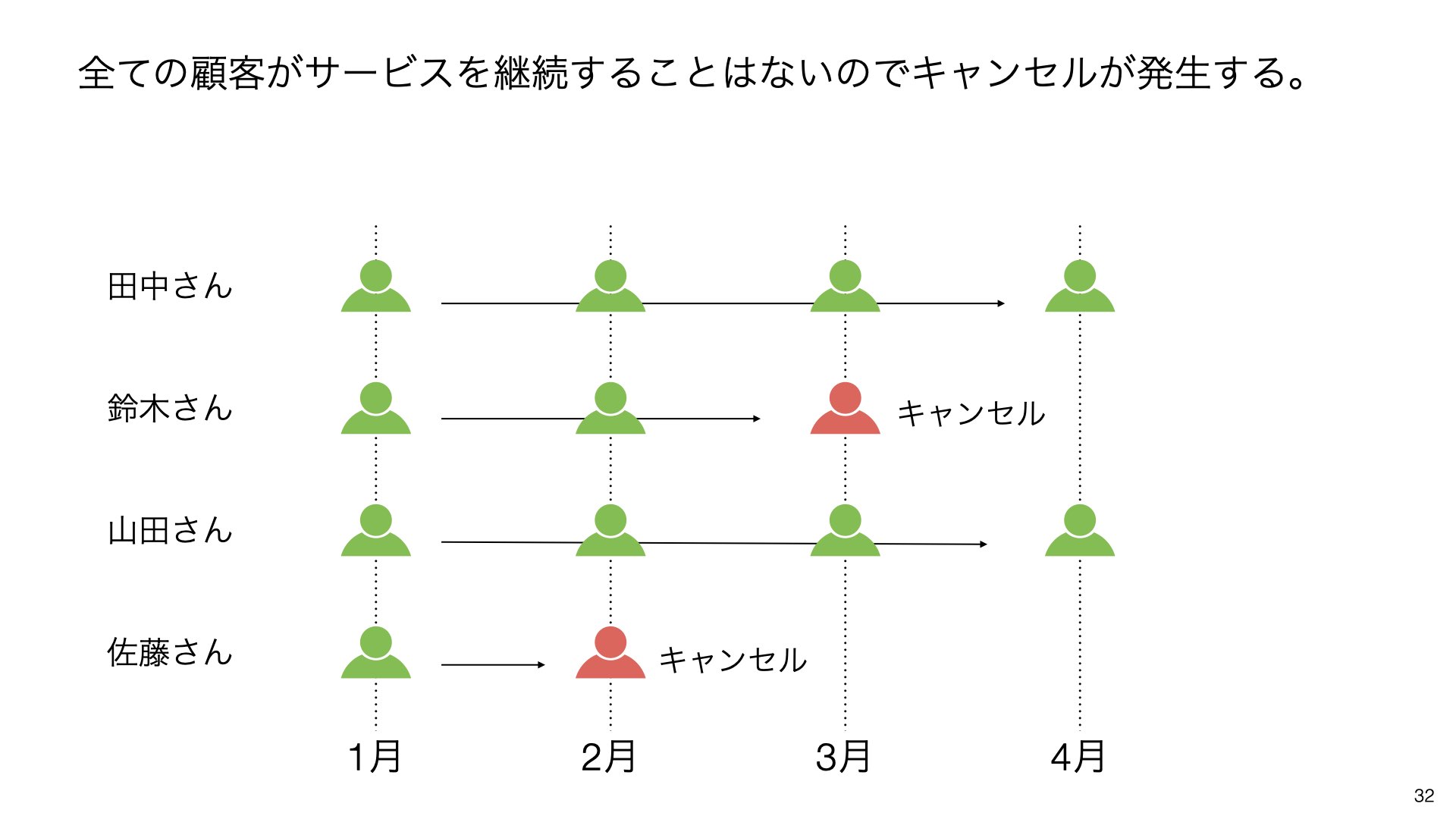
しかし、全ての顧客がサービスを継続するわけではありません。一部の顧客は期間中に解約(キャンセル)することがあります。これが生存分析における「イベント発生」にあたります。
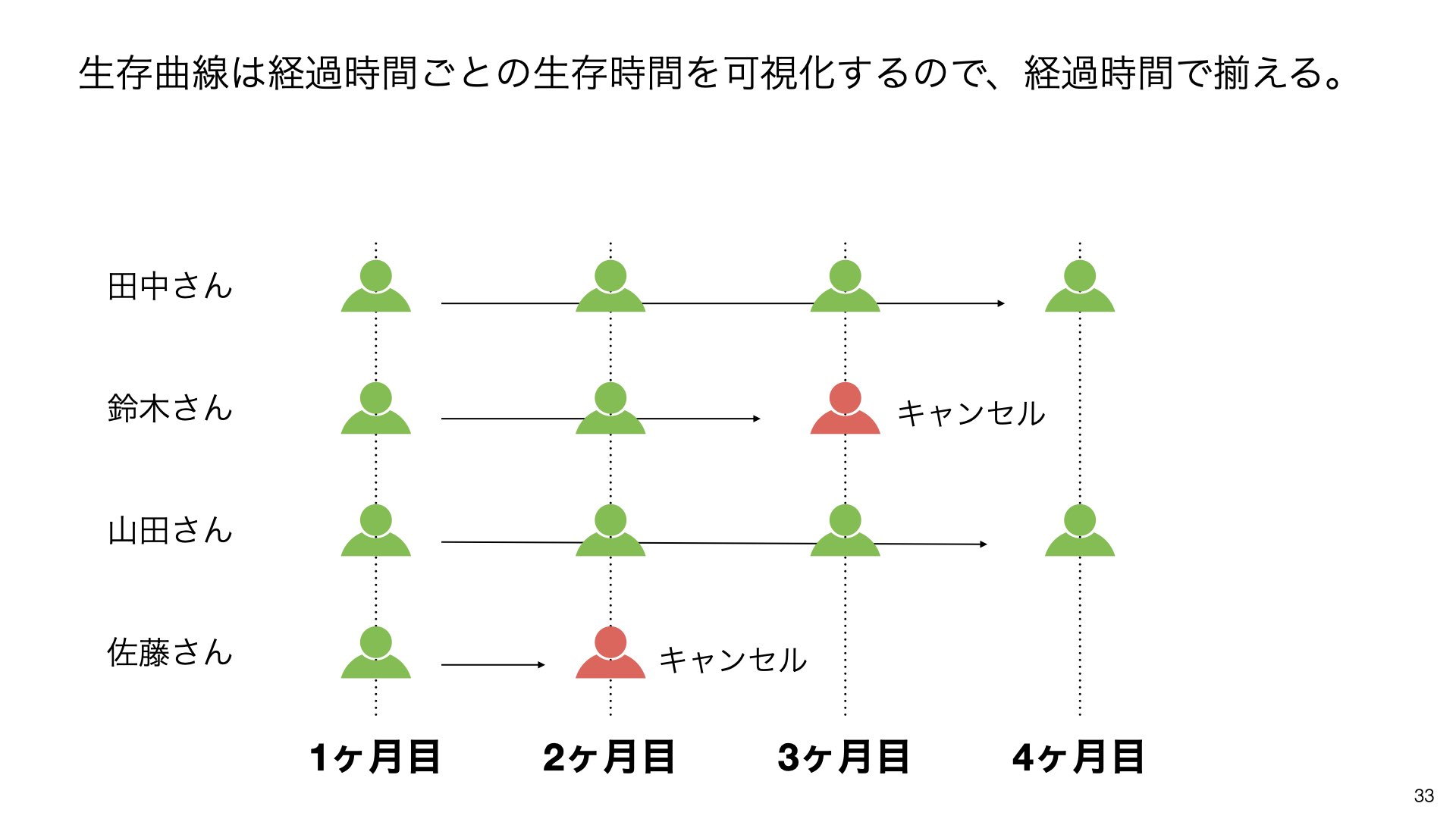
生存曲線は、このような経過時間ごとの生存時間を可視化するために使用されます。横軸は経過時間、縦軸は生存率を表します。
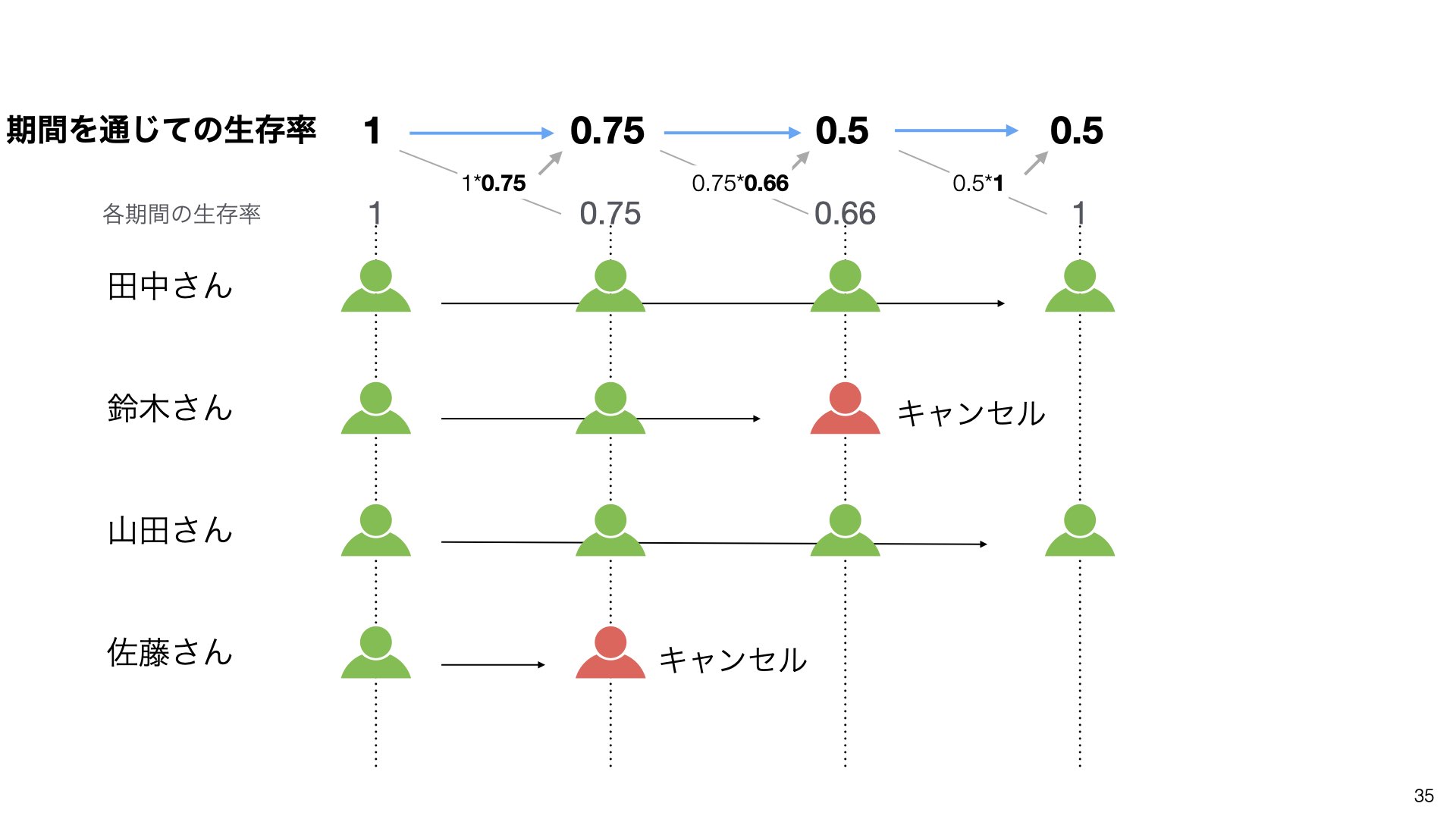
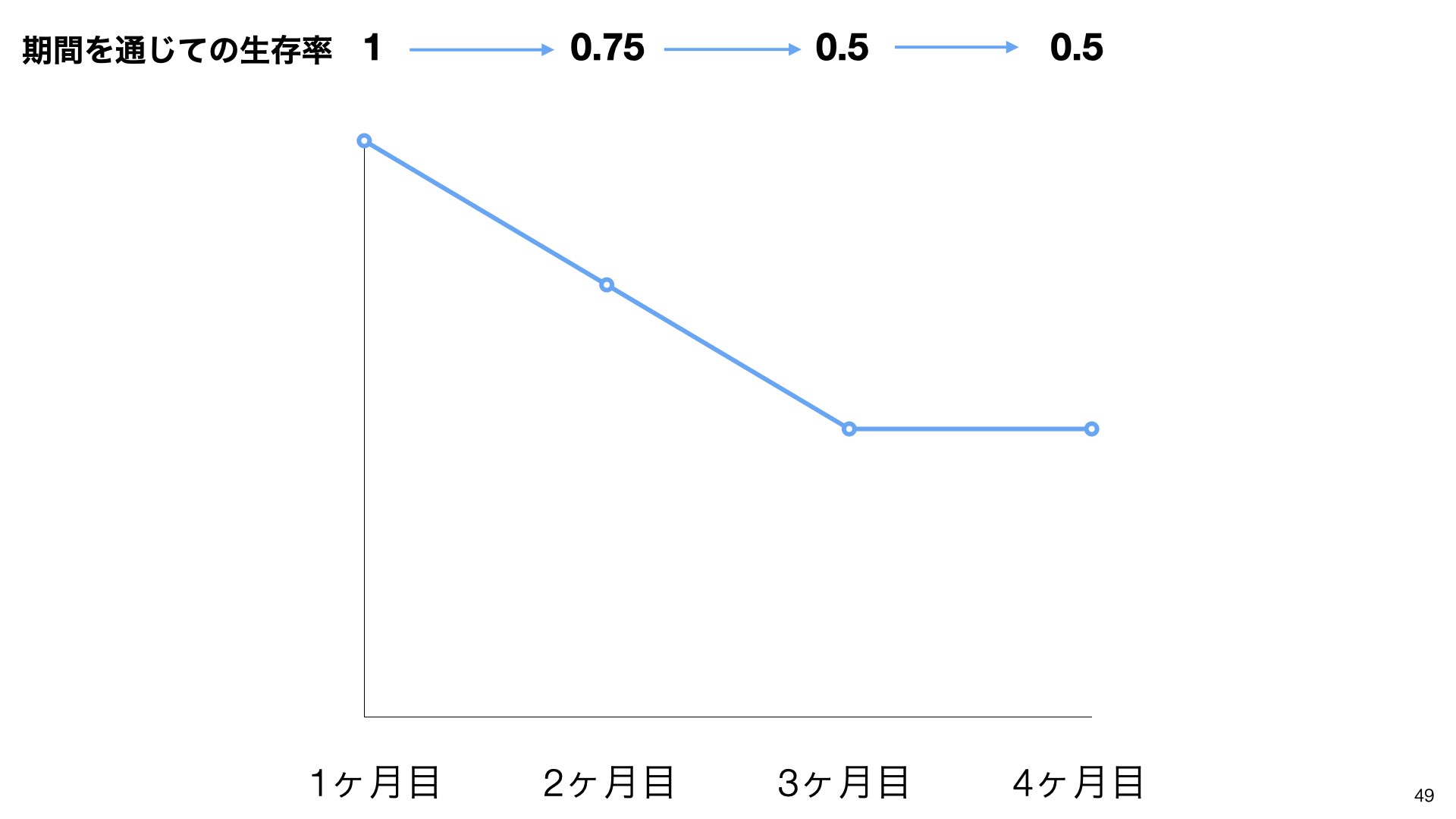
各月の生存率を具体的に見てみると、1ヶ月目は1(100%)、2ヶ月目は0.75(75%)、3ヶ月目は0.66(66%)、4ヶ月目は1(100%)となります。
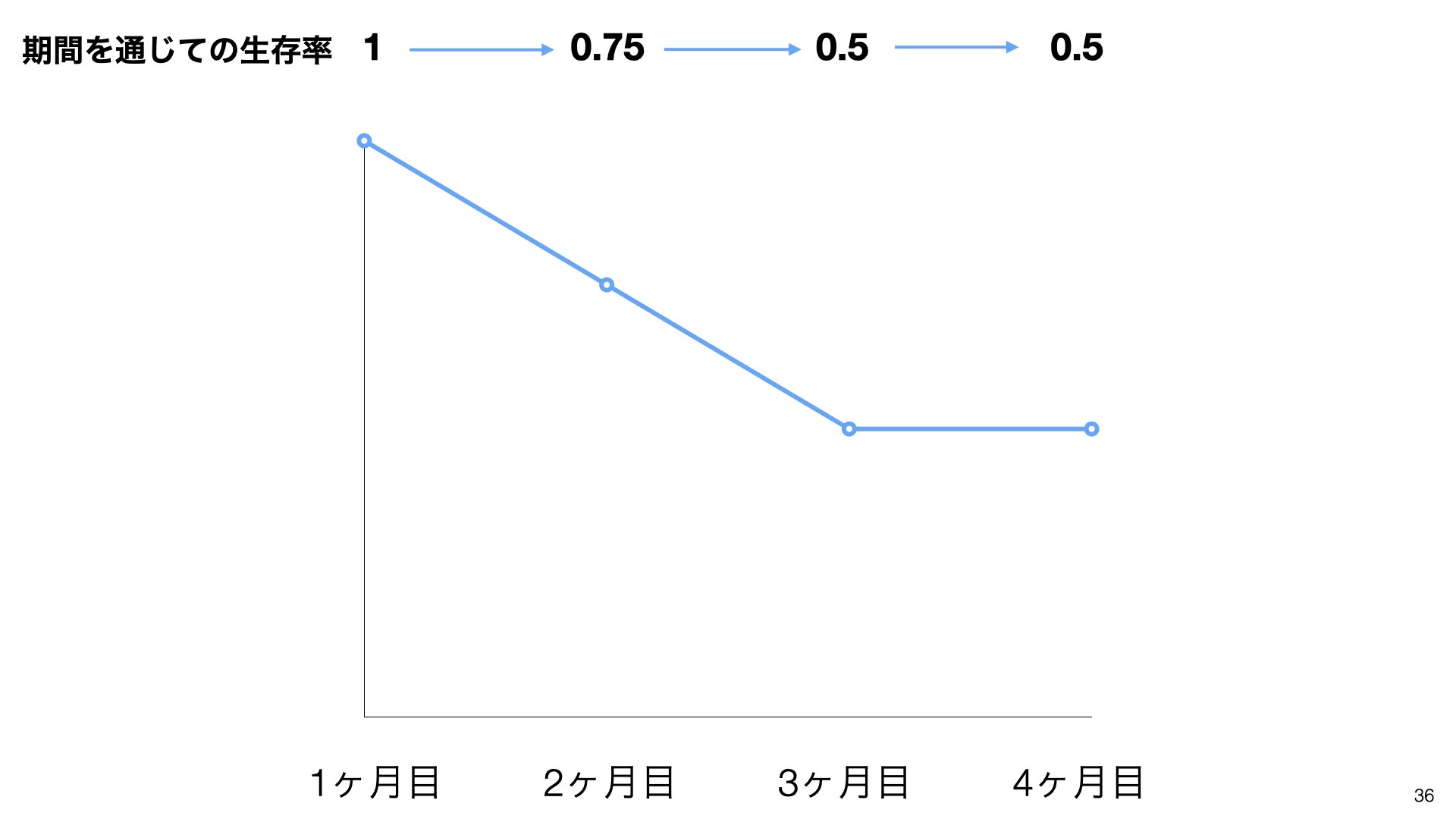
期間を通じての生存率は、各期間の生存率を掛け合わせて計算します。1×0.75=0.75、0.75×0.66=0.5、0.5×1=0.5となります。
この計算結果をグラフにプロットすると、階段状の生存曲線が完成します。
実際のカプランマイヤー法の打ち切り処理
現実の世界では、顧客は異なるタイミングでサービスを利用し始めます。そのため、観察期間の終了時点で、一部の顧客の最終的な結果が分からない状況が発生します。
例えば、山田さんは2ヶ月目から、佐藤さんは3ヶ月目から、高橋さんは4ヶ月目からサービスを開始したとします。この場合、観察期間中に全ての顧客について何ヶ月間サービスを使っているかを把握することができます。
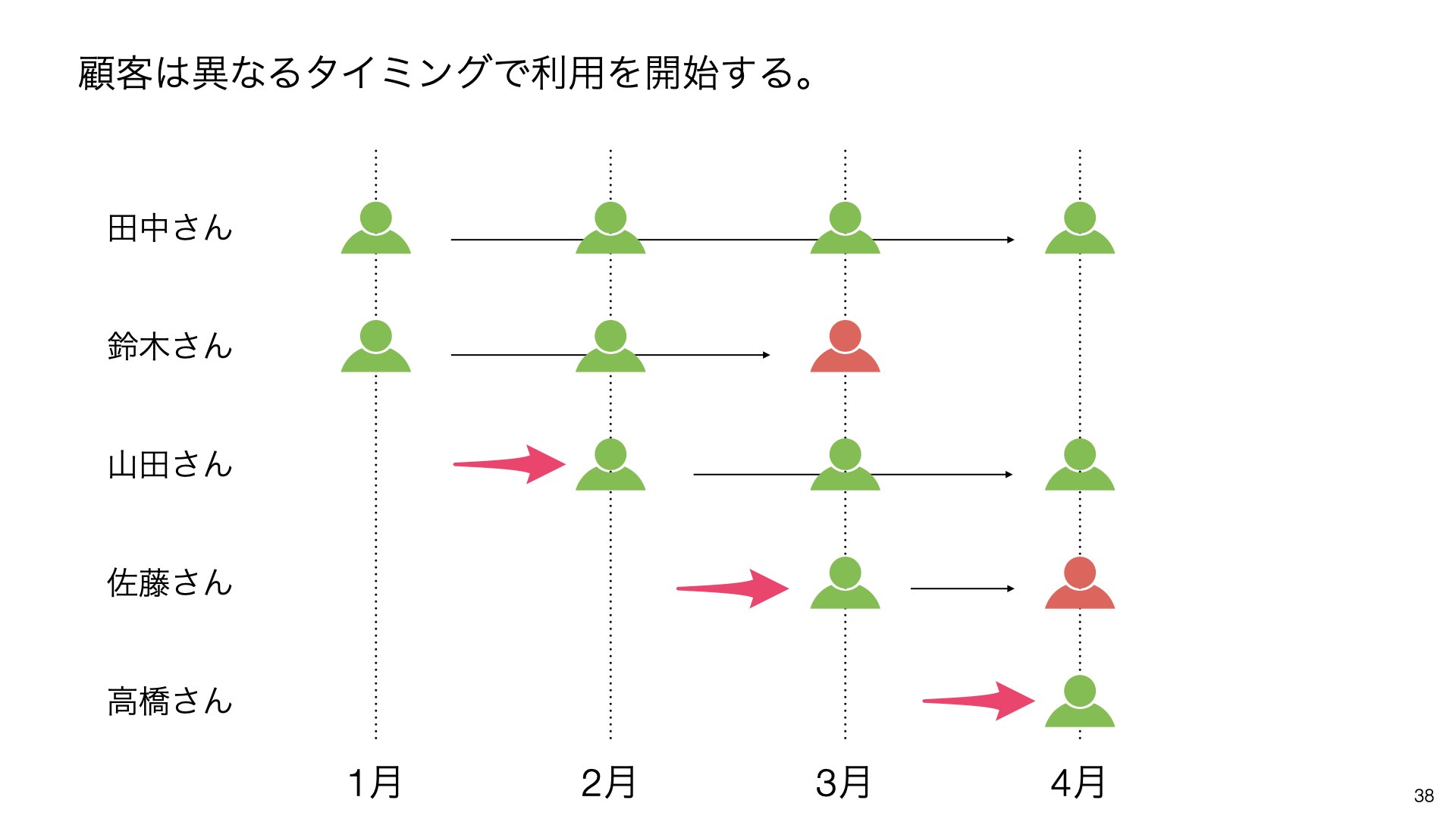
しかし、観察期間が終了した時点で、まだサービスを継続している顧客がいます。全ての顧客を何ヶ月間サービスを使っているかで捉えることができます。
打ち切りの問題
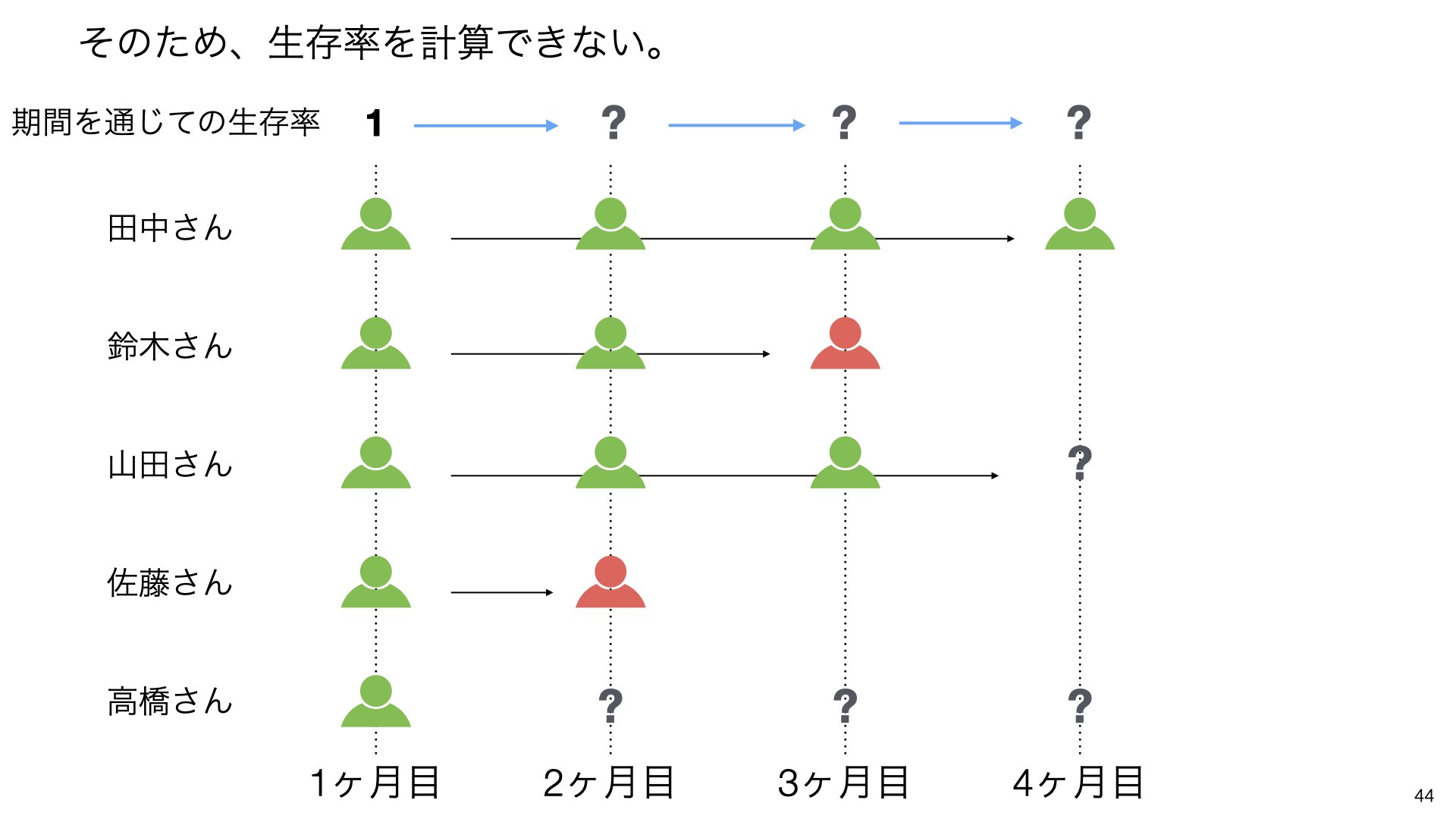
ここで、生存率を計算する際に一つの問題が生じます。
山田さんと高橋さんの継続状況がわからない期間があります。山田さんは4ヶ月目以降、高橋さんは2ヶ月目以降の状況が不明です。
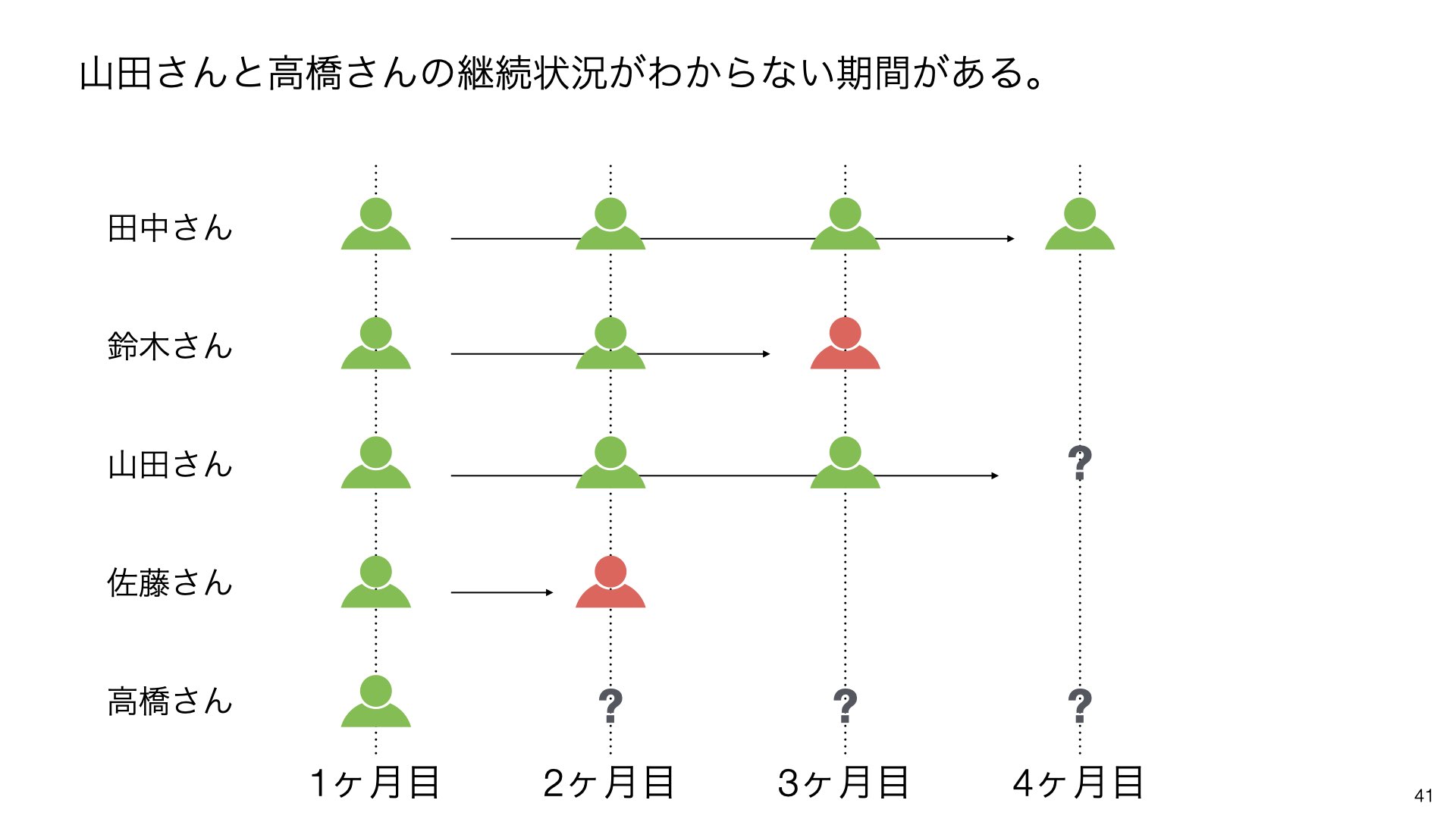
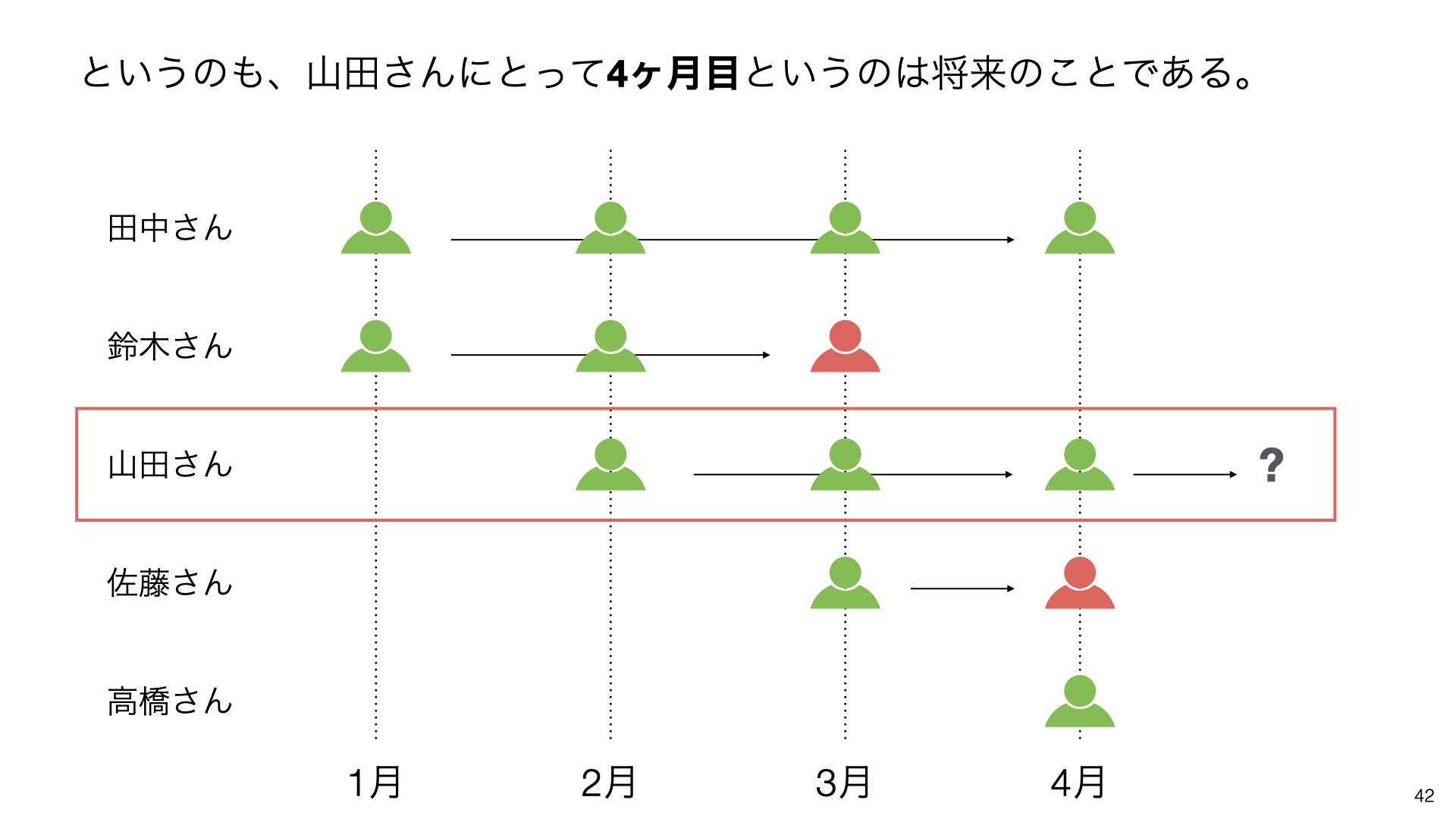
このような状況では、将来のことであるため、山田さんにとって4ヶ月目以降、高橋さんにとって2ヶ月目以降は将来の出来事となります。
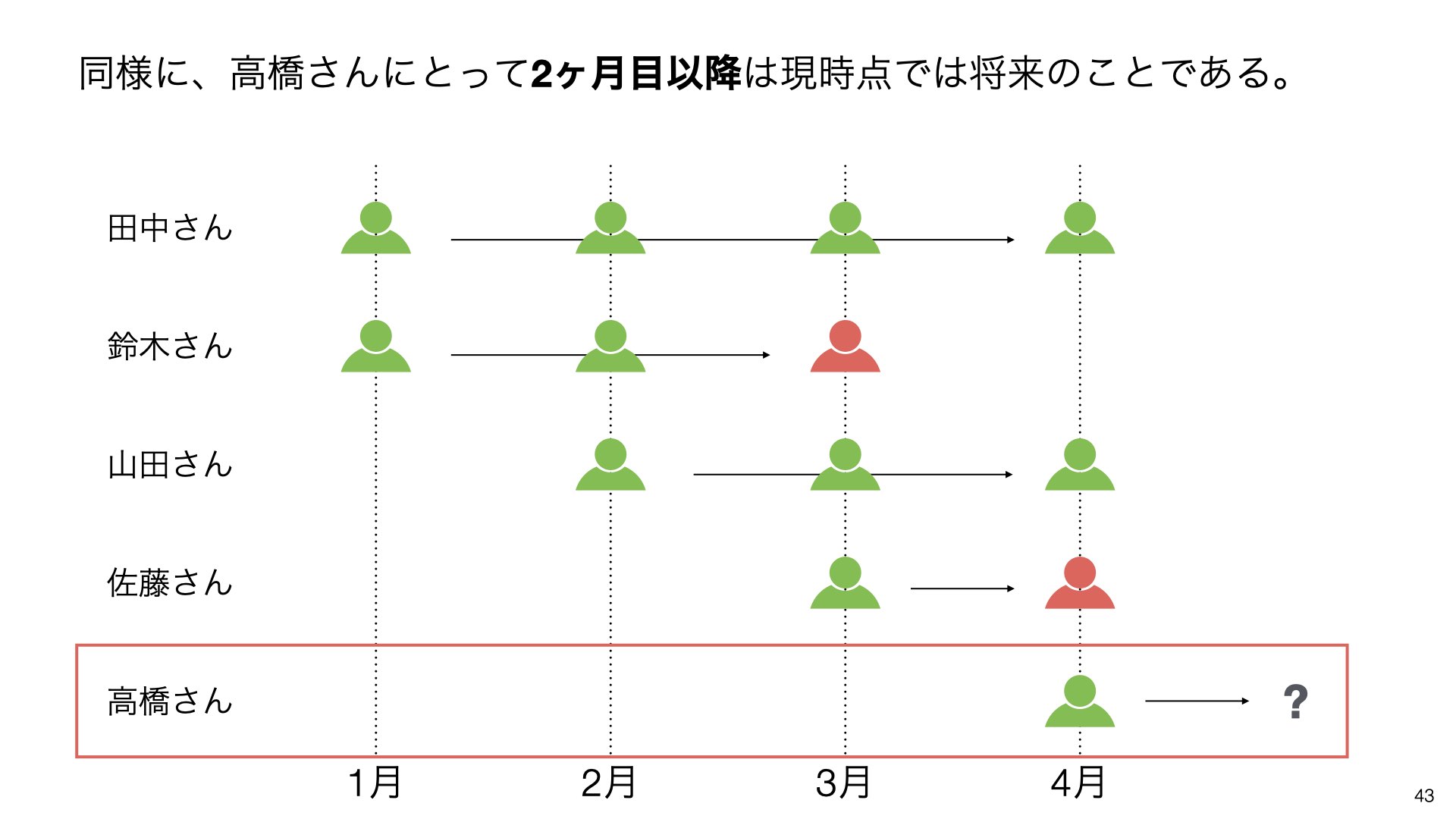
同様に、高橋さんにとって2ヶ月目以降は現時点では将来のことであるため、結果が不明です。
そのため、通常の方法では生存率を計算できません。期間を通じての生存率が「?」となってしまいます。
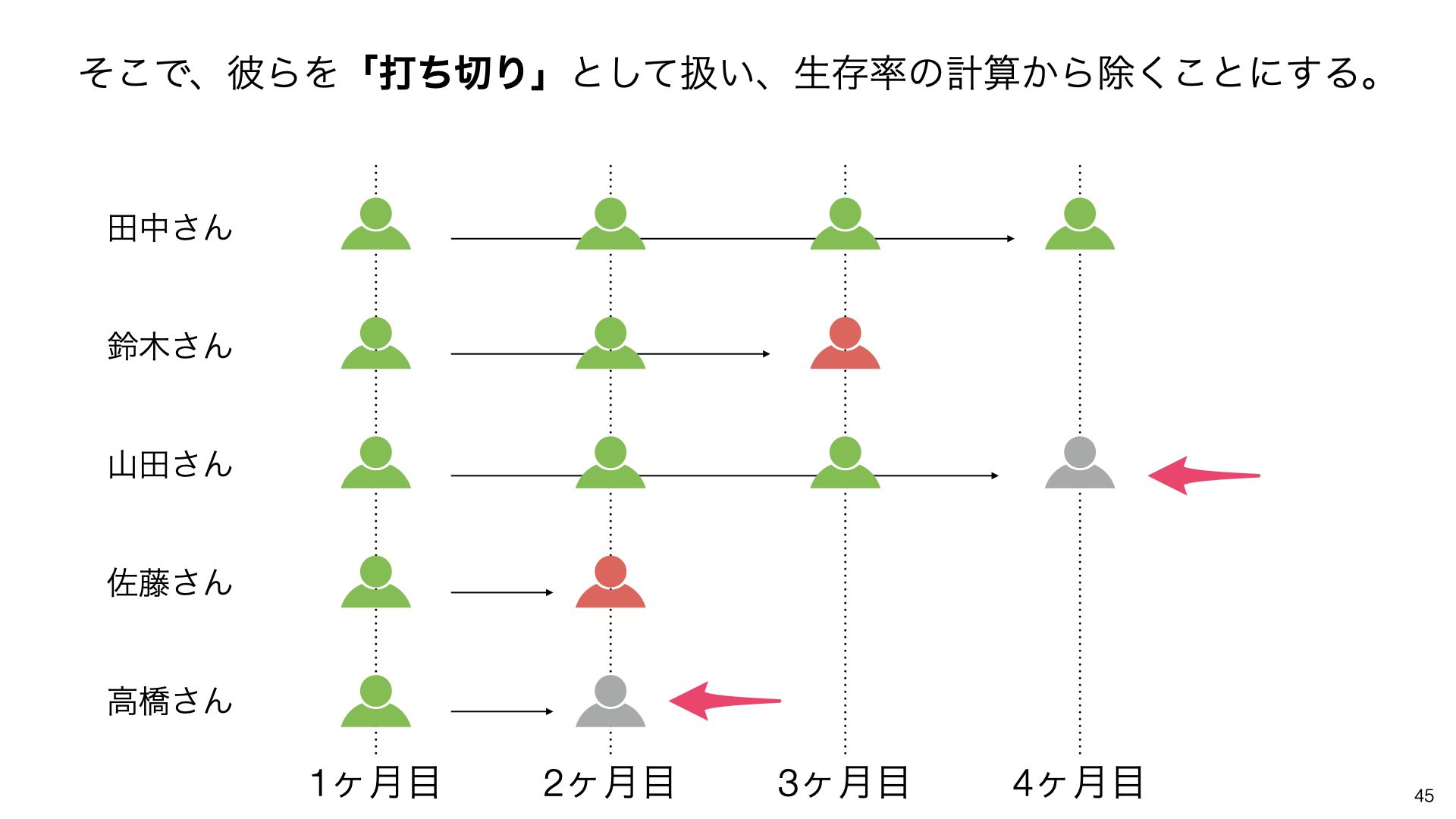
打ち切り処理の実施
そこで、これらの顧客を「打ち切り」として扱い、生存率の計算から除くことにします。
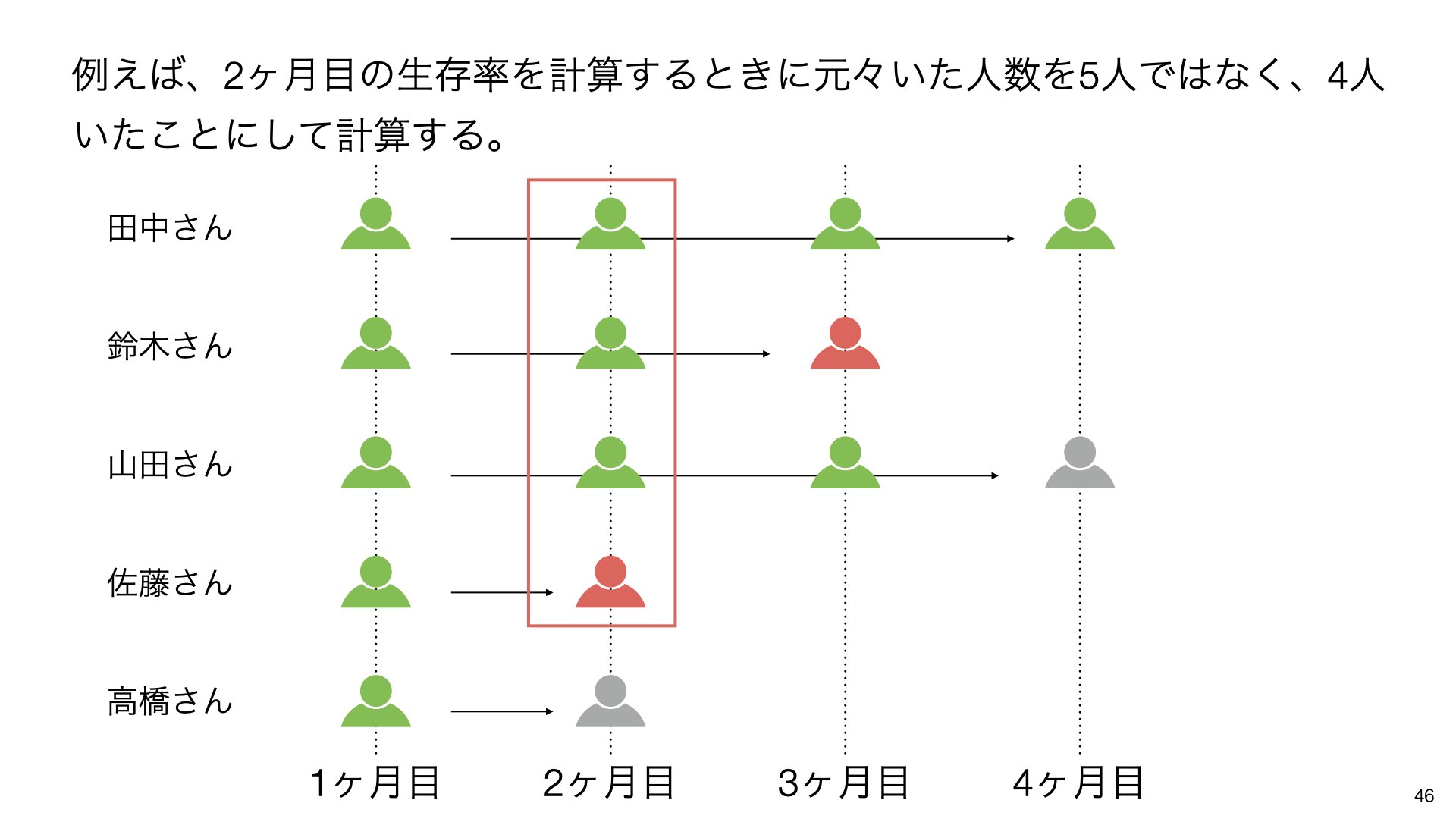
例えば、2ヶ月目の生存率を計算するときに、元々いた人数を5人ではなく、4人(高橋さんを除く)として計算します。
この修正により、各月の生存率を正確に計算できるようになります。3/4=0.75、2/3=0.66、1/1=1となります。
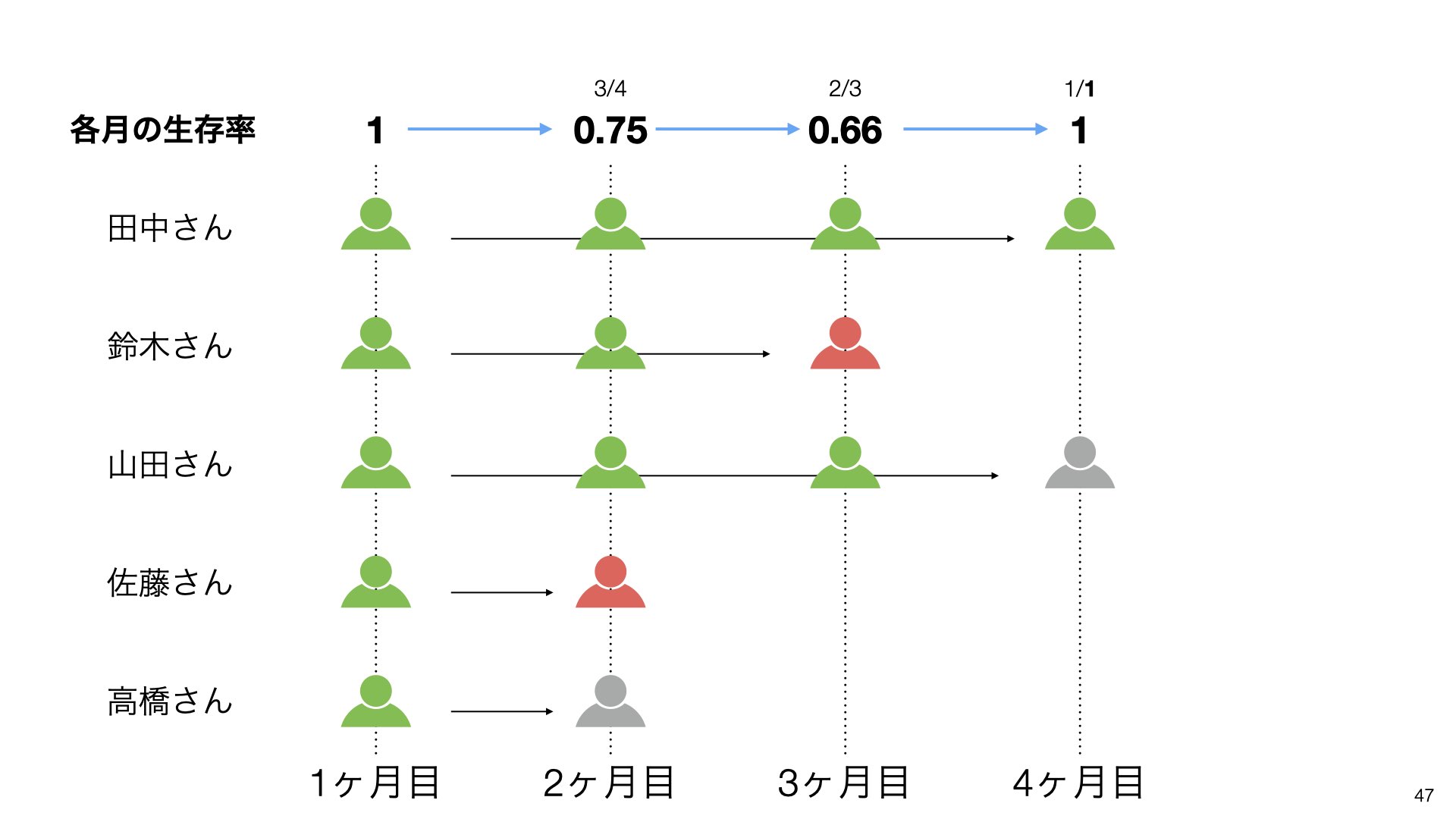
期間を通じての生存率も、1×0.75=0.75、0.75×0.66=0.5、0.5×1=0.5として正しく計算できます。
最終的に、打ち切りを適切に処理した生存曲線が完成します。
動画
生存曲線やカプランマイヤー法について紹介している動画は以下をご覧ください。
まとめ
カプランマイヤー法は、打ち切りデータが存在する状況での生存分析を可能にする強力な手法です。この手法の最も重要な特徴は、打ち切り処理により観察期間中に結果が確認できない対象者を適切に除外できることです。
また、段階的計算を行うことで、各時点での生存率を段階的に計算し、全体の生存率を正確に求めることができます。さらに、医療分野での治療効果の分析だけでなく、ビジネス分野でのサービス継続率や商品の故障率分析など、幅広い分野で活用できる実用性の高さも特徴です。
この手法により、不完全なデータからでも信頼性の高い生存率推定が可能になり、意思決定に役立つ情報を得ることができます。