Introduction to One-Way ANOVA in Exploratory
This is an introductory note on how to run One-Way ANOVA in Exploratory and how to interpret various tabs that are automatically generated.
One-Way ANOVA is one of the statistical testing methods and can be used to test if the difference in multiple means among multiple groups is significant.
As the name suggests, there is another version of One-Way ANOVA, which is called Two-Way ANOVA. In this document, we'll focus on One-Way ANOVA.
Objective and Data
We have this clinical trial data about the effectiveness of two drugs - Drug A and Drug B.
The data can be downloaded from here.
In order to see the effectiveness we have assign patients with a certain type of disorder to 3 groups of Drug A, Drug B, and Placebo (No Drug).
After having the patients taking their assigned drugs we measured how much their symptom improved. Bigger 'Improvement' numbers mean the better improvement.
We can visualize the means of the improvements among the 3 groups as below.
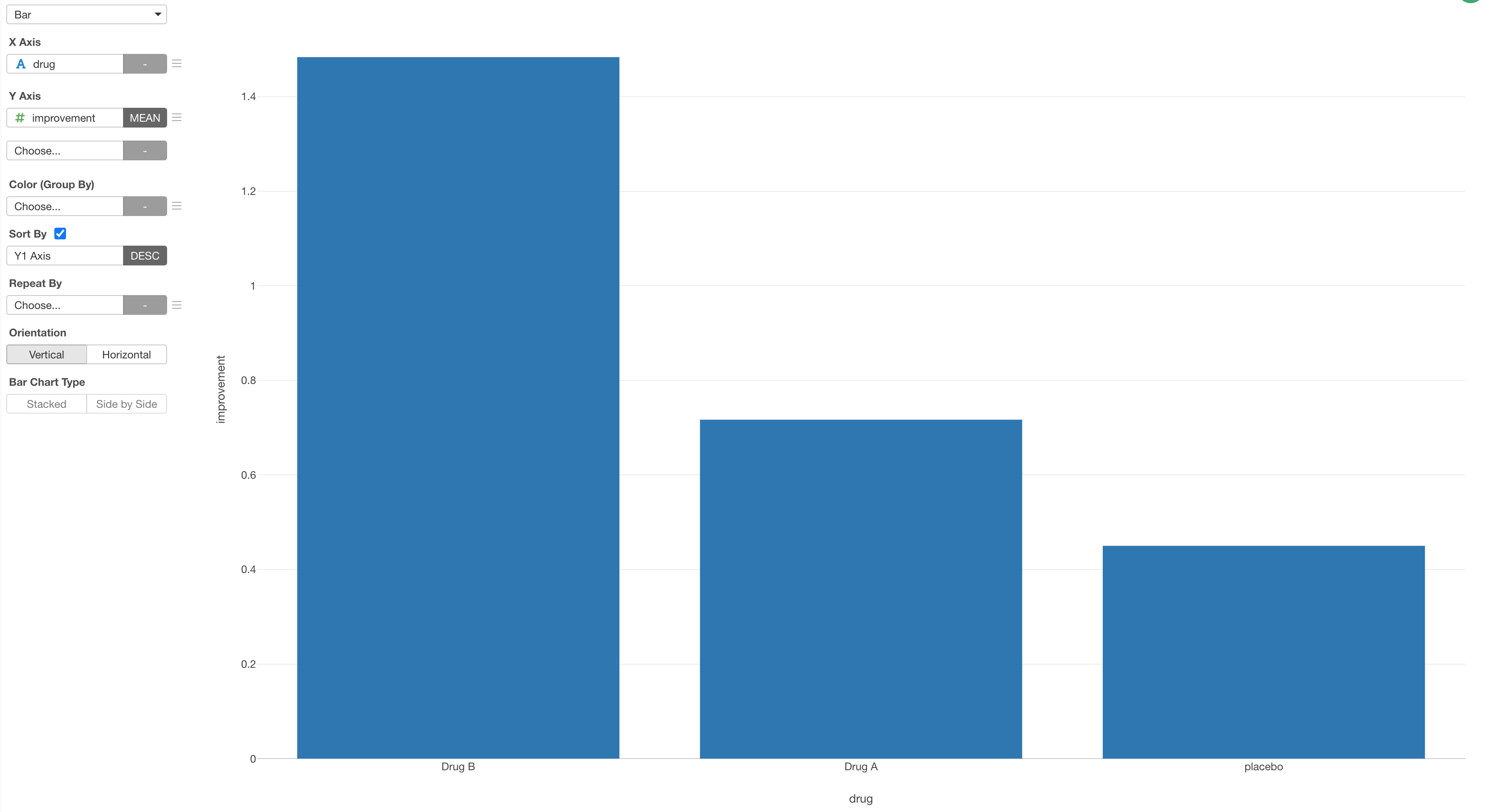
Now the questions is, are these differences statistically significant or just a consequence of randomness.
Run One-Way ANOVA
Under the Analytics view, select 'One-Way ANOVA' from the Type.

And select the 'Improvement' column for the Target Variable and the 'drug' column for the Explanatory Variable, and click the Run button.
You will see a Summary tab being generated.

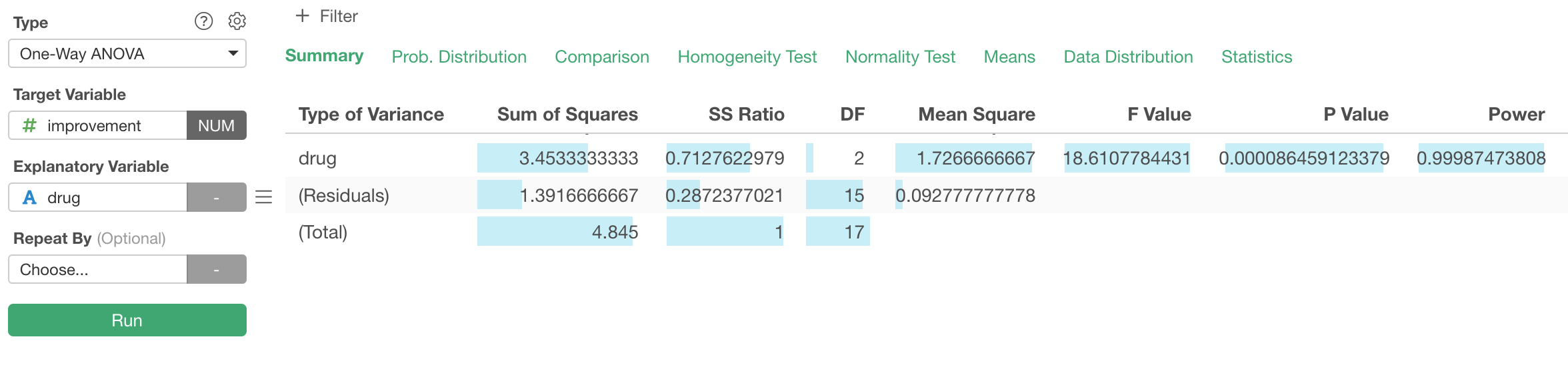
Result Summary
Significance
The first row shows various metrics about the explanatory variable 'drug'.
The Sum of Squares indicates the total variance of the 3 means (the means for each group of Drug A, Drug B, and Placebo). The Mean Square is the mean of the variance.
The F Value is calculated as a ratio of the explained variance (due to the model) compared against the unexplained variance (residuals).
The P Value indicates a probability of observing the difference between several means from the multiple groups if we accept a null hypothesis (assumption) that there is no difference among them.
Given that the P Value here is less 0.05 (5%), we can conclude that the difference among the groups is statistically significant (assuming that the threshold value is 0.05).
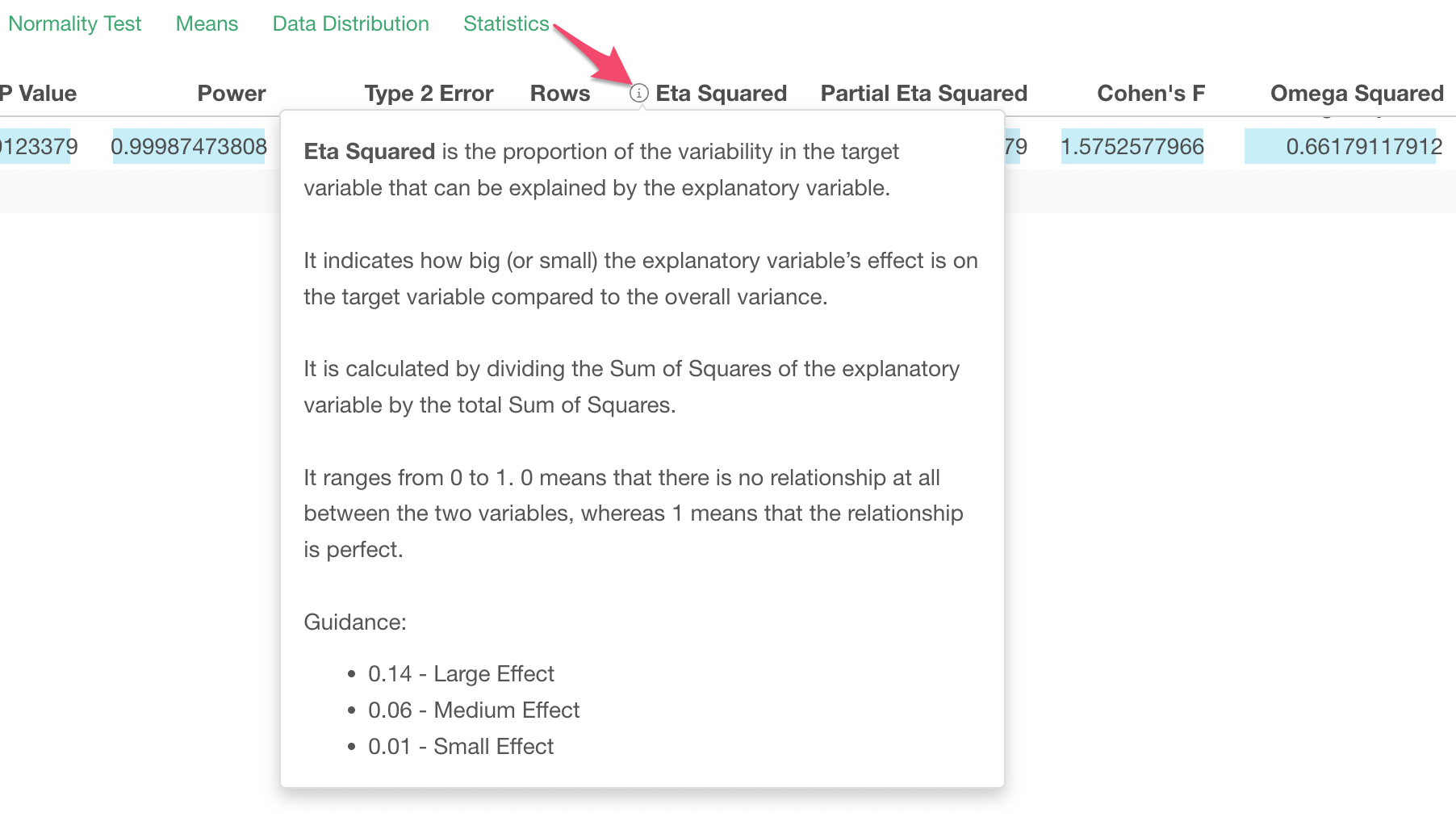
Effect Size
Testing if the difference or the effect is significant or not is one thing, but even when it's significant we want to know how big is the difference or the effect.
There are 4 effect size metrics provided under the Summary table.
- Eta Squared
- Partial Eta Squared
- Cohen's F
- Omega Squared

You can see what these metrics mean by clicking on the information icon in the column header.
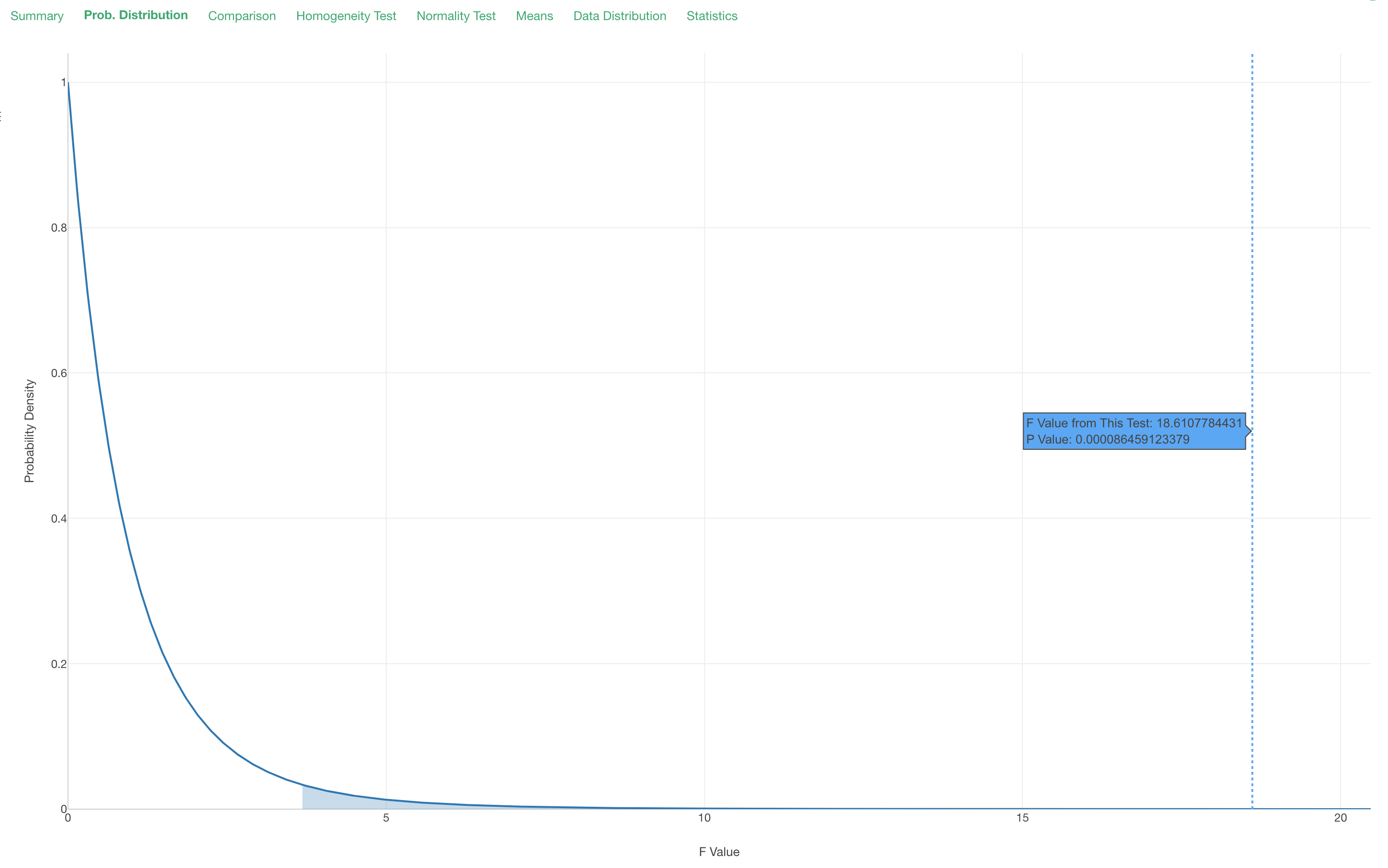
Probability Distribution
Under the Probability Distribution tab, you can see where the given F value from this test is located on the underlying probability curve 'F distribution' as the blue dotted vertical line.
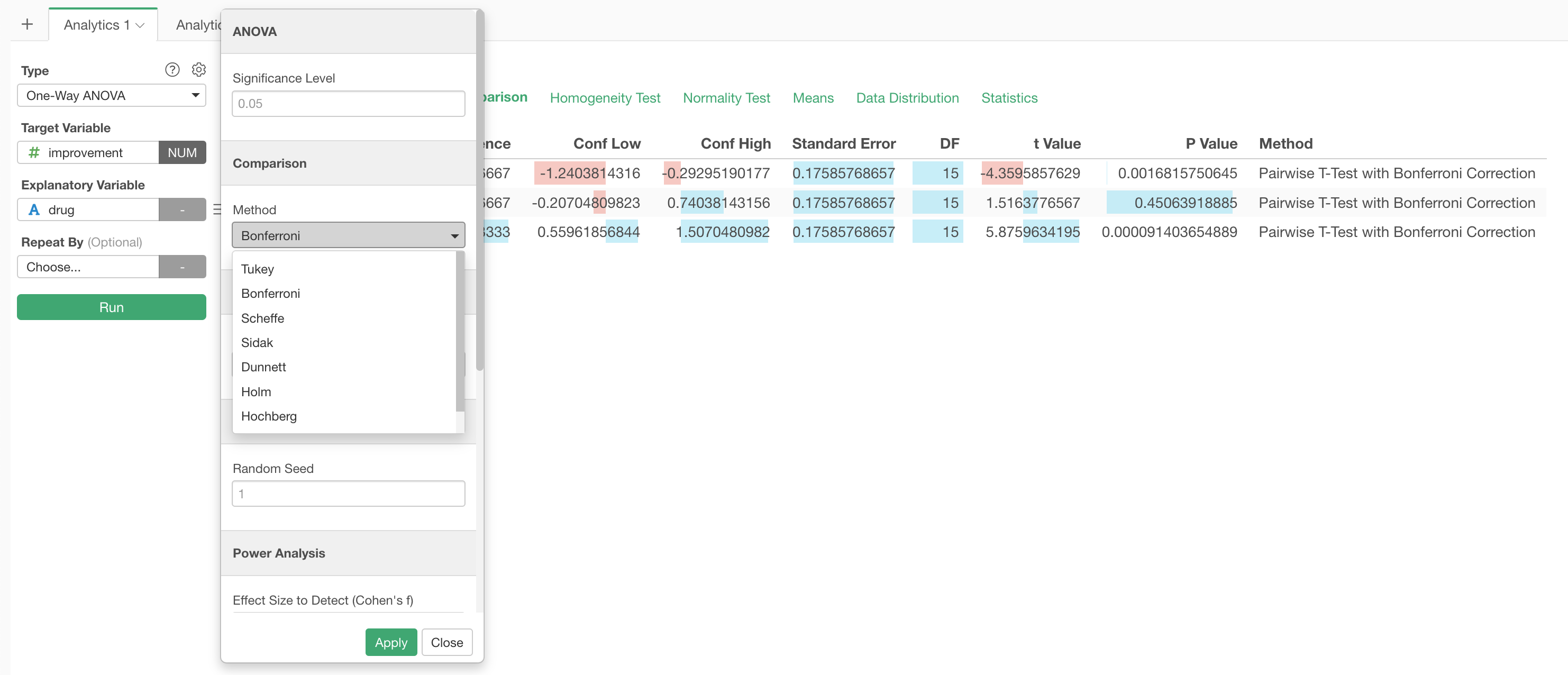
Comparison
Under the Comparison tab, you can see the result of 'Post Hoc Test', which test the significance of each pair of the groups. In this case, we have 3 groups - Drug A, Drug B, and Placebo - we have 3 combinations of the pairs.

The default method for this multiple comparisons is Tukey's HSD Test. Based on the result, we can conclude that the difference between Drug A and Drug B and the one between Drug A and Placebo are significant, but the difference between Drug B and Placebo is not.
Given this is a post hoc test you might want to add a correction to the P values. You can choose from various methods for the correction in the Property dialog.
Assumption Check
ANOVA test is designed based on a few assumptions. You can check the following two assumptions about the underlying data in Exploratory.
- The data variances among Groups are equal.
- The data is normally distributed.
Homogeneity Test for Equal Variance

The null hypothesis is there is no difference (equal) in the variance among the groups.
If the P value is less than a threshold value (it's 0.05 (5%) by default in Exploratory) we can reject the null hypothesis hence there is a difference and this invalidates the assumption.
If the P value is greater than a threshold value (it's 0.05 (5%) by default in Exploratory) then we can't reject the null hypothesis hence the variances are equal and the assumption is valid.
Normality Test for Normal Distribution

The null hypothesis is there is no difference between a normal distribution and the distribution of data in hands.
If the P value is less than a threshold value (it's 0.05 (5%) by default in Exploratory) we can reject the null hypothesis hence the underlying data distribution is difference from the normal distribution and this invalidates the assumption.
If the P value is greater than a threshold value (it's 0.05 (5%) by default in Exploratory) then we can't reject the null hypothesis hence the underlying data distribution is equal to the normal distribution and the assumption is valid.
Descriptive Statistics
You can see the descriptive statics of the data in various ways.
Means
Under the Means tab, you can see the means of multiple groups and their 95% confidence interval.
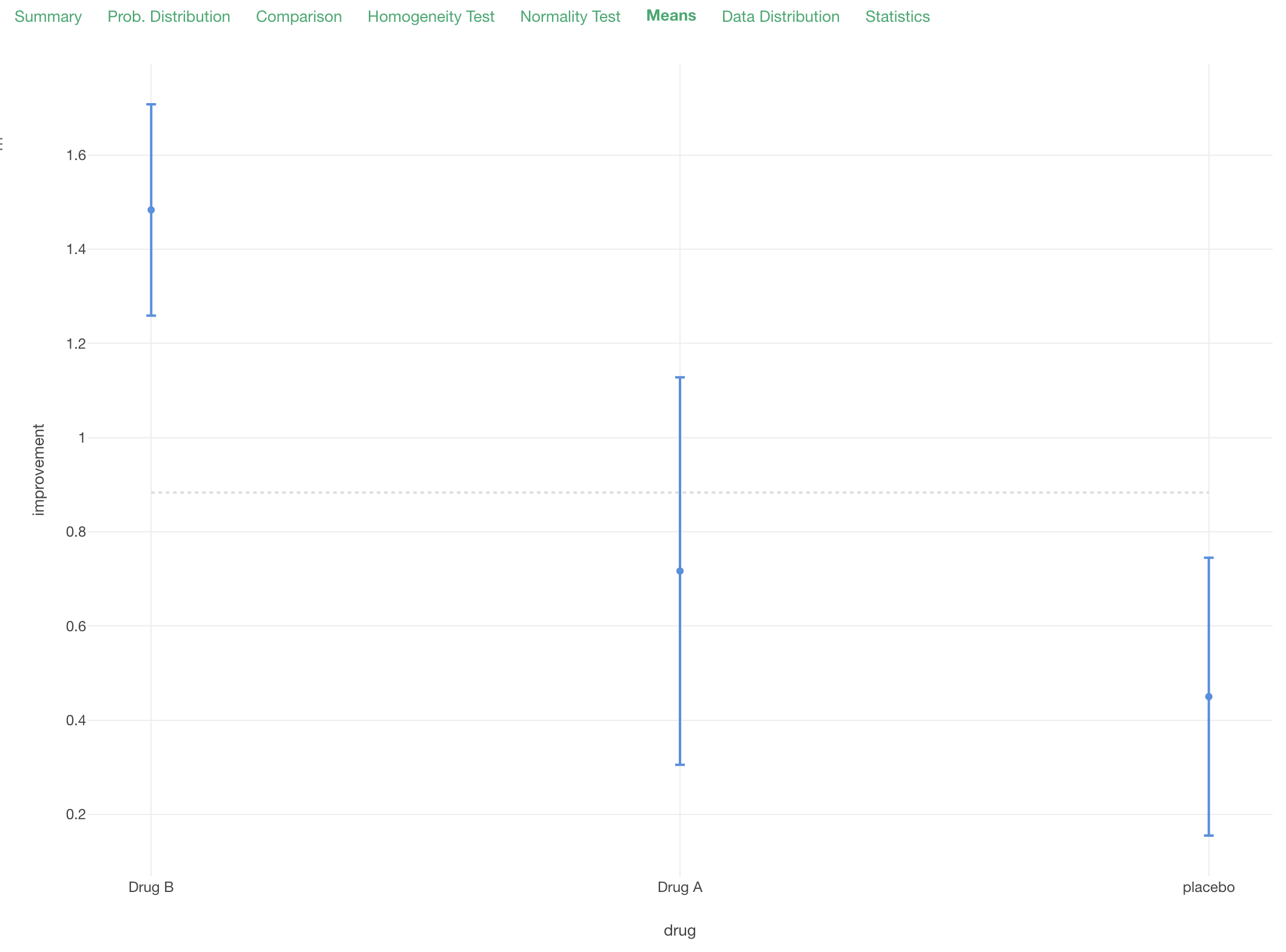
This is an error bar chart that visualize the means and the confidence intervals and shows you the summary the underlying data.
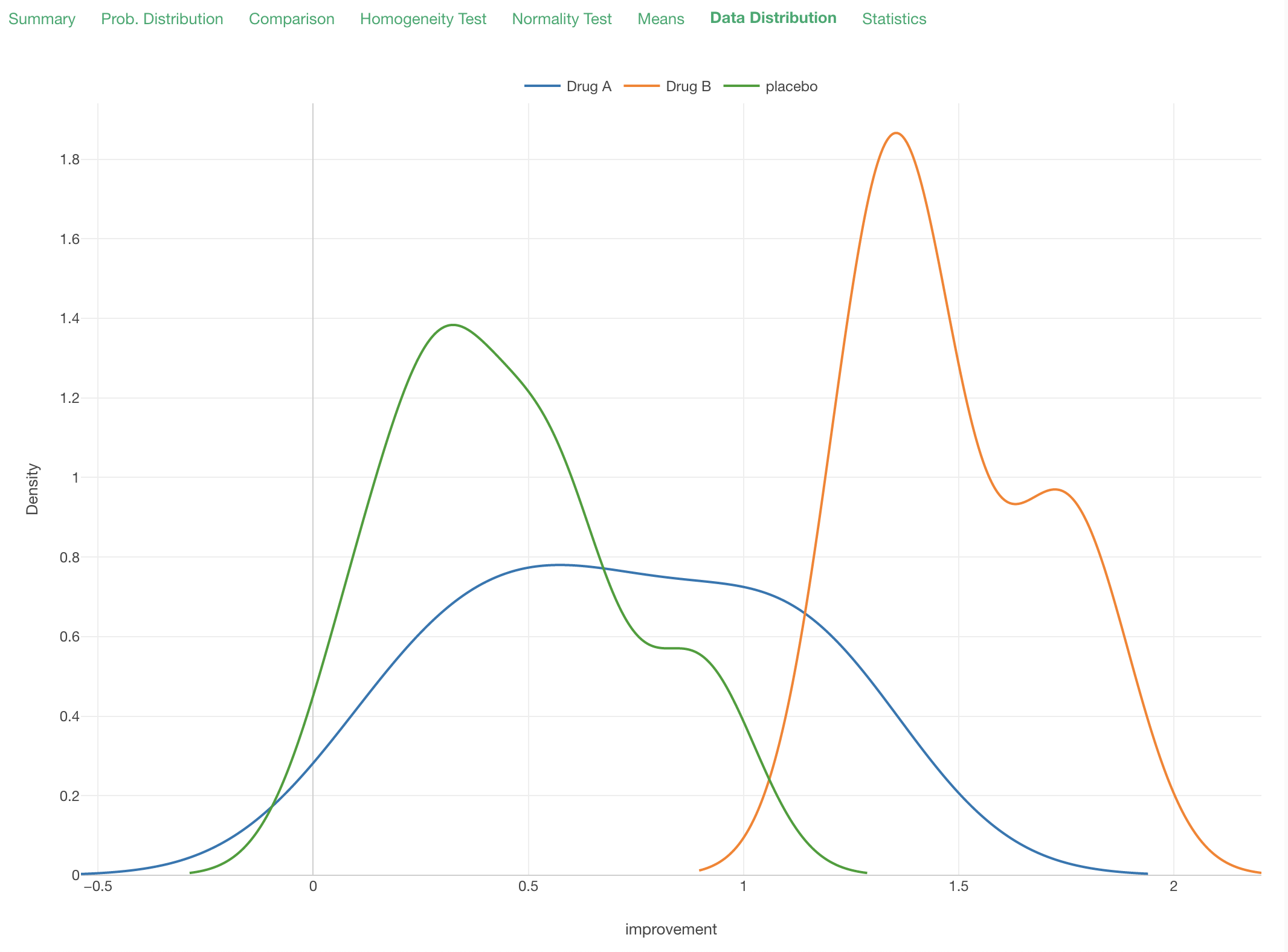
Data Distribution
Under the Data Distribution tab, you can see how the data is distributed by each group.
Statistics
Under the Statistics tab, you can see various summary statistics for each group.
