主成分分析の紹介

このノートでは主成分分析について簡単に紹介させていただきます。

主成分分析は、よく次元削減の手法として使われるアルゴリズムの一つで、元のデータに含まれる情報量を極力失わないようにしながらも少ない数の「次元（変数）」で表現することができます。

さらには、複数の変数間の関係を可視化したり、元のデータの中にあるパターンや特徴を可視化したりすることにもよく使われたりします。

必要なデータの形式

主成分分析を実行する際には、1行が1観測対象となっているデータを使う必要があります。また、変数の列には数値型の列のみが選択できます。

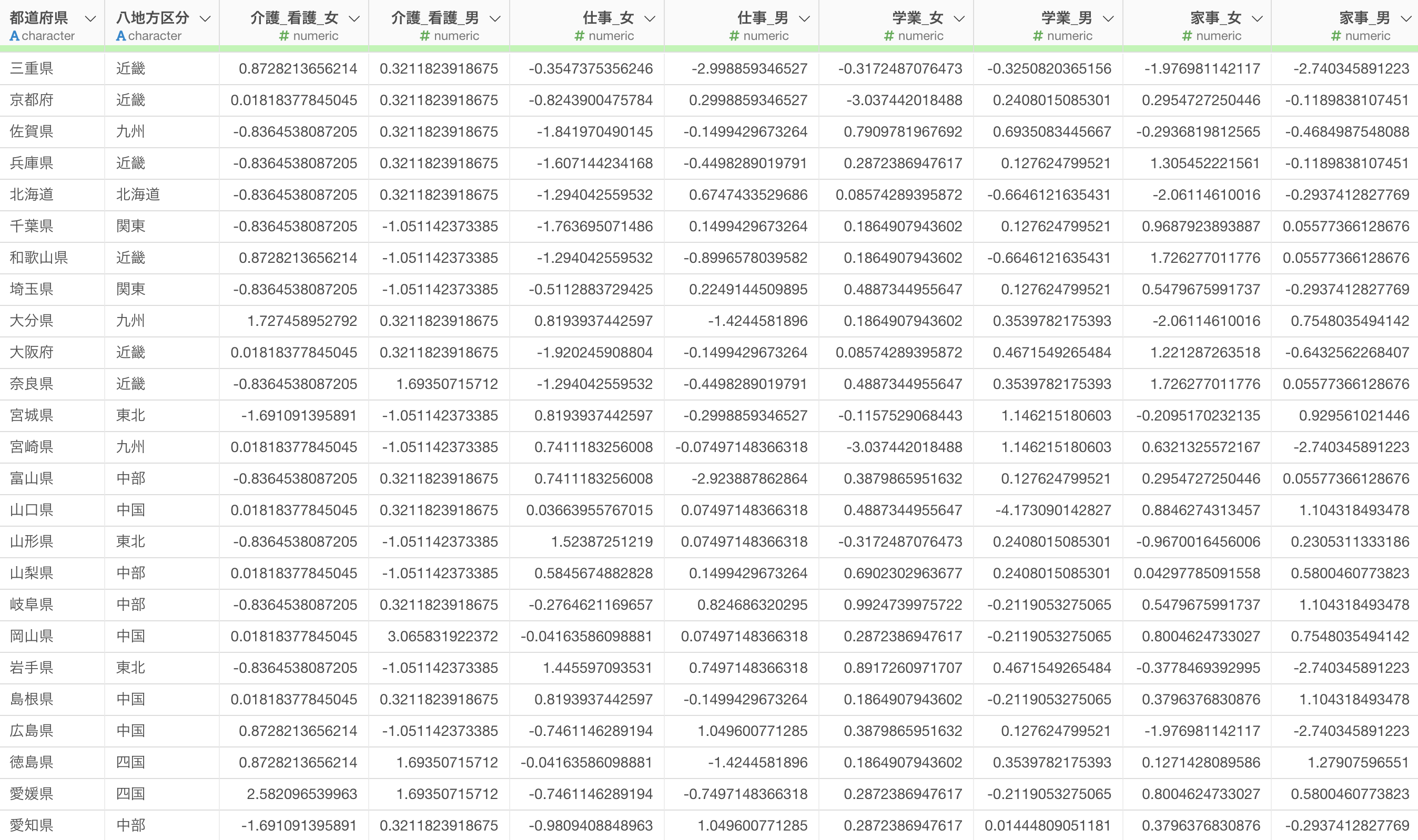
そこで、今回はサンプルデータとして、都道府県ごとの時間の使い方のデータを使用します。

このデータは、1行が1都道府県となっていて、列には仕事や家事、学業などにどれだけの時間を使っているかの列が性別ごとにあります。

アナリティクスビューを開き、タイプに「主成分分析」を選択します。

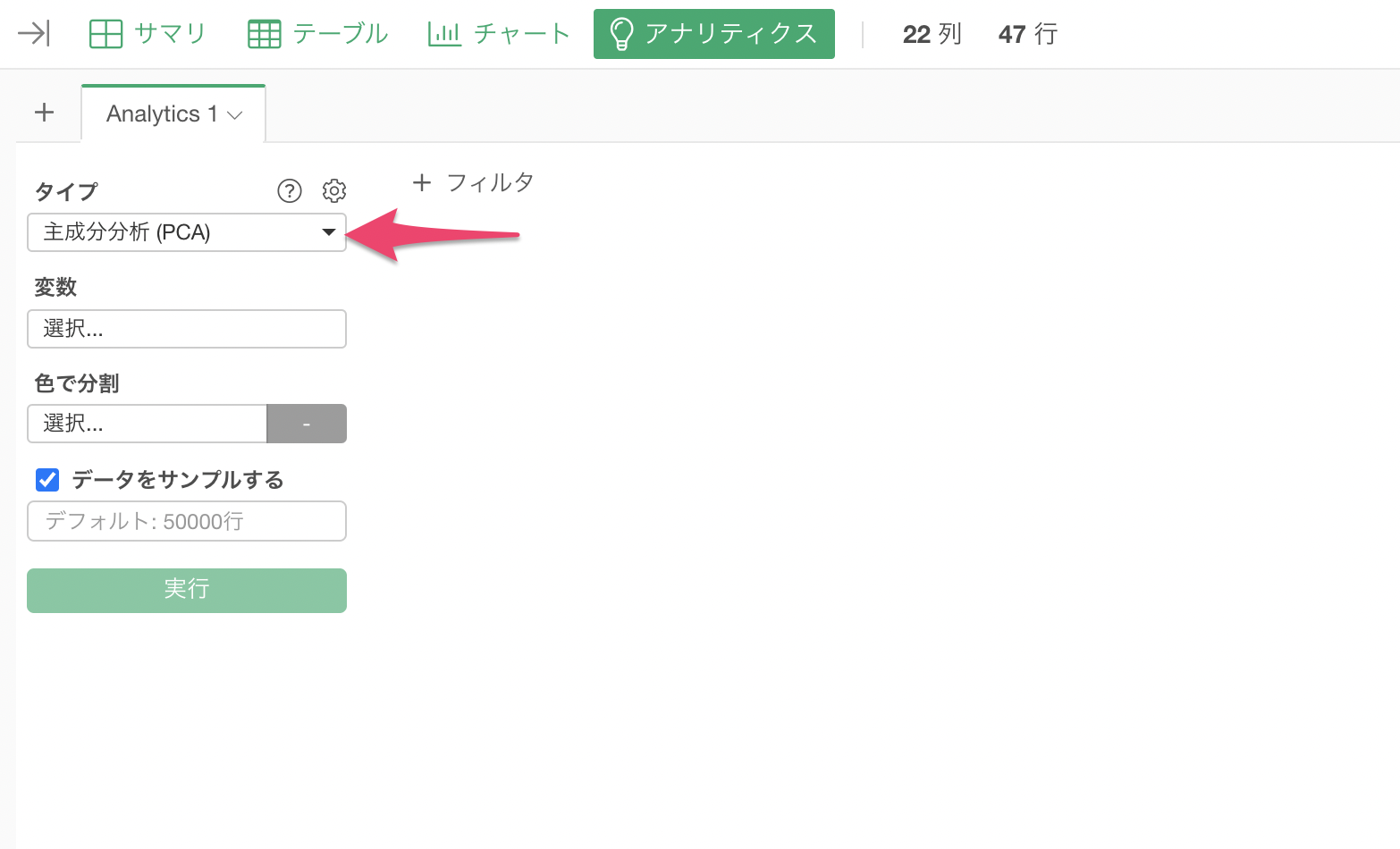
変数の列をクリックして、主成分分析に使用する列を選択します。シフトキーを押すことで、複数の列を一気に選択できます。

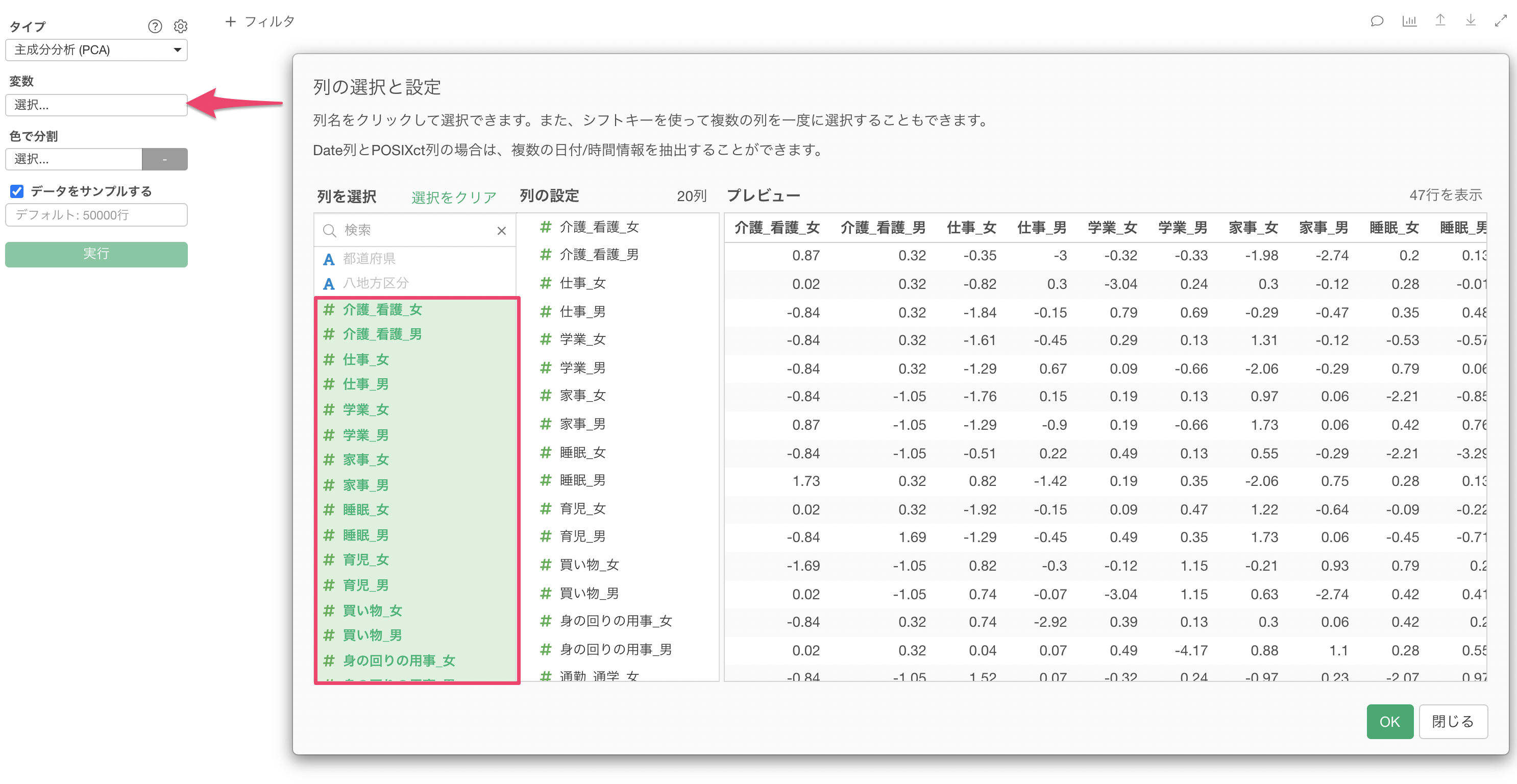
列の指定が完了したら実行することで、主成分分析の結果が表示されます。

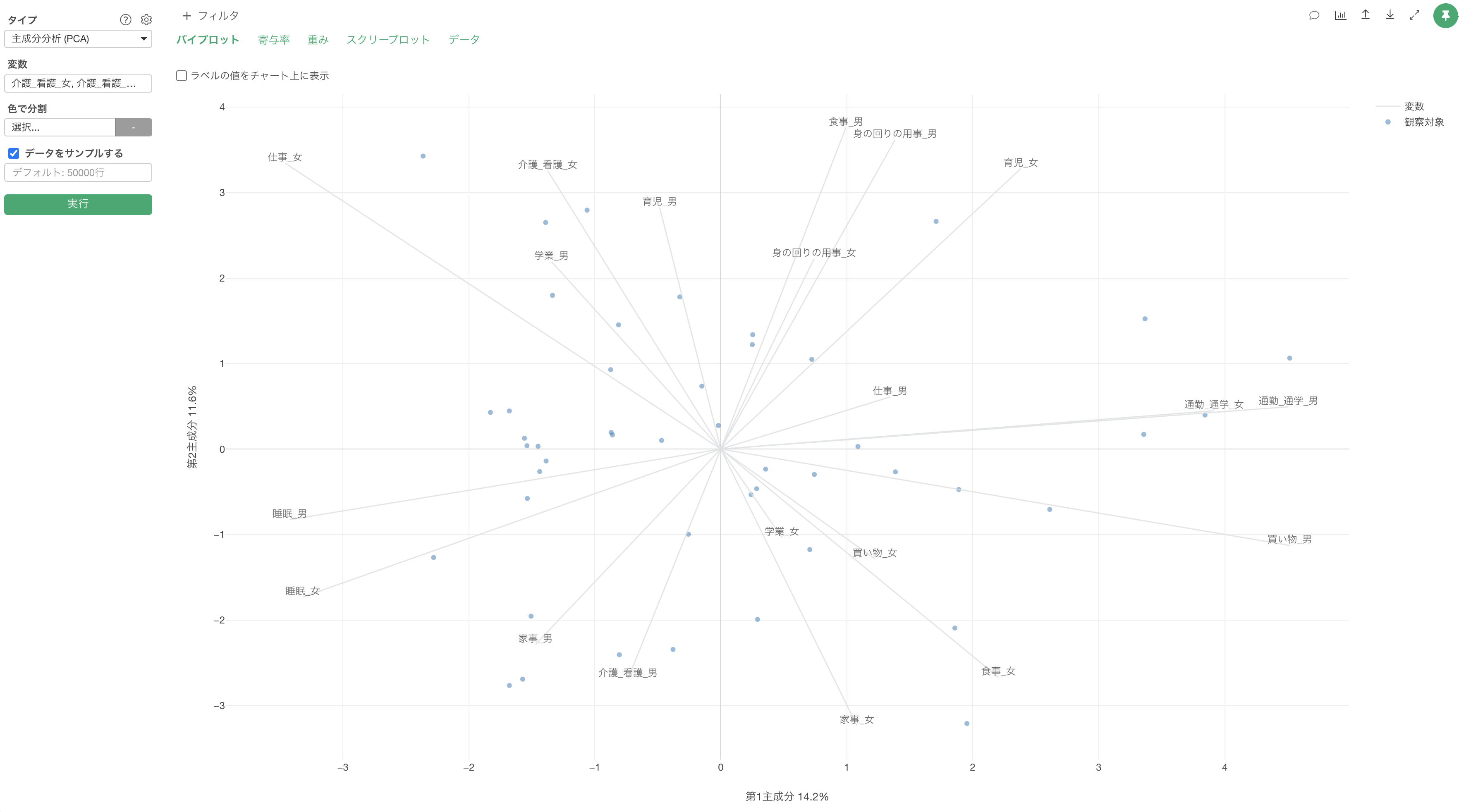
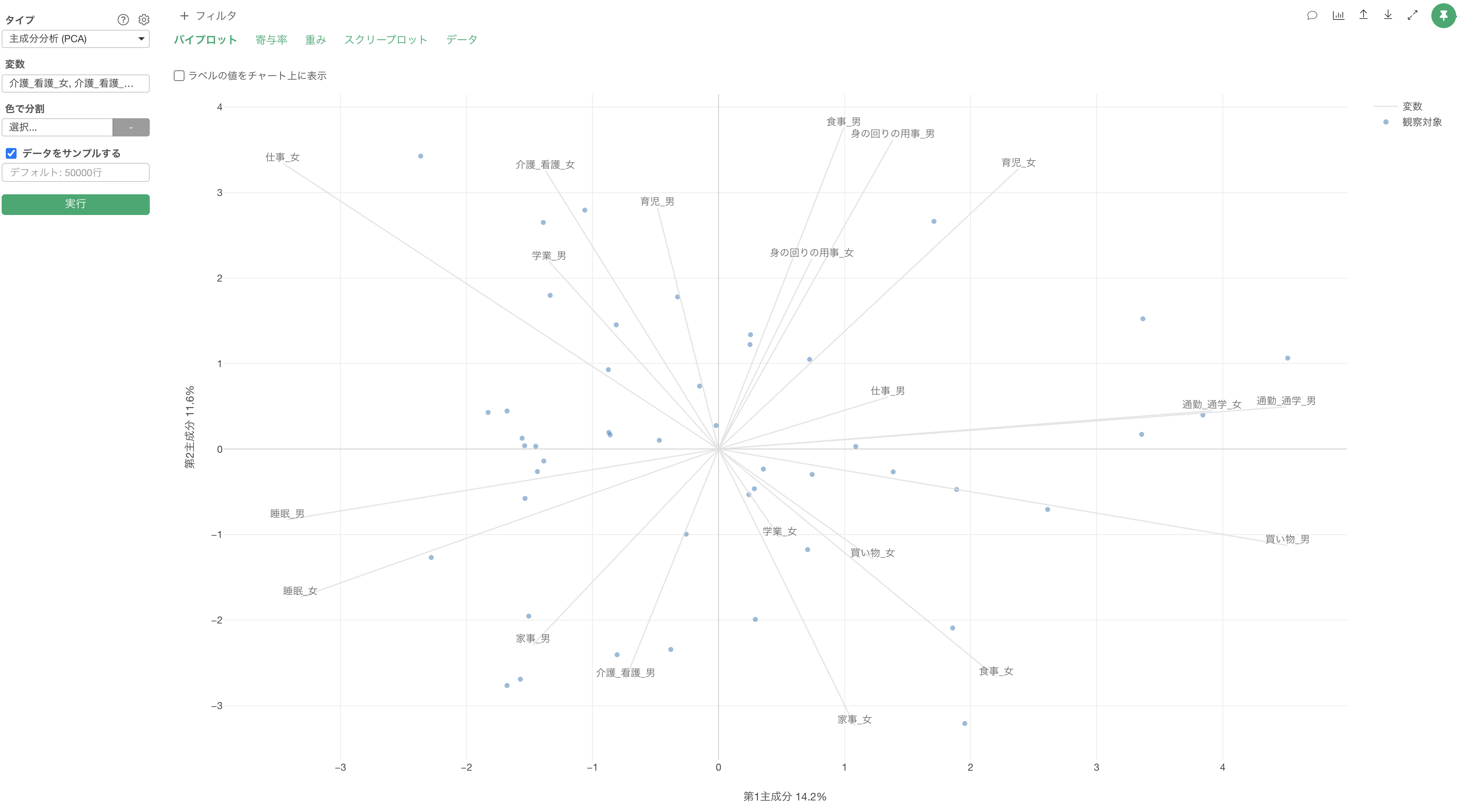
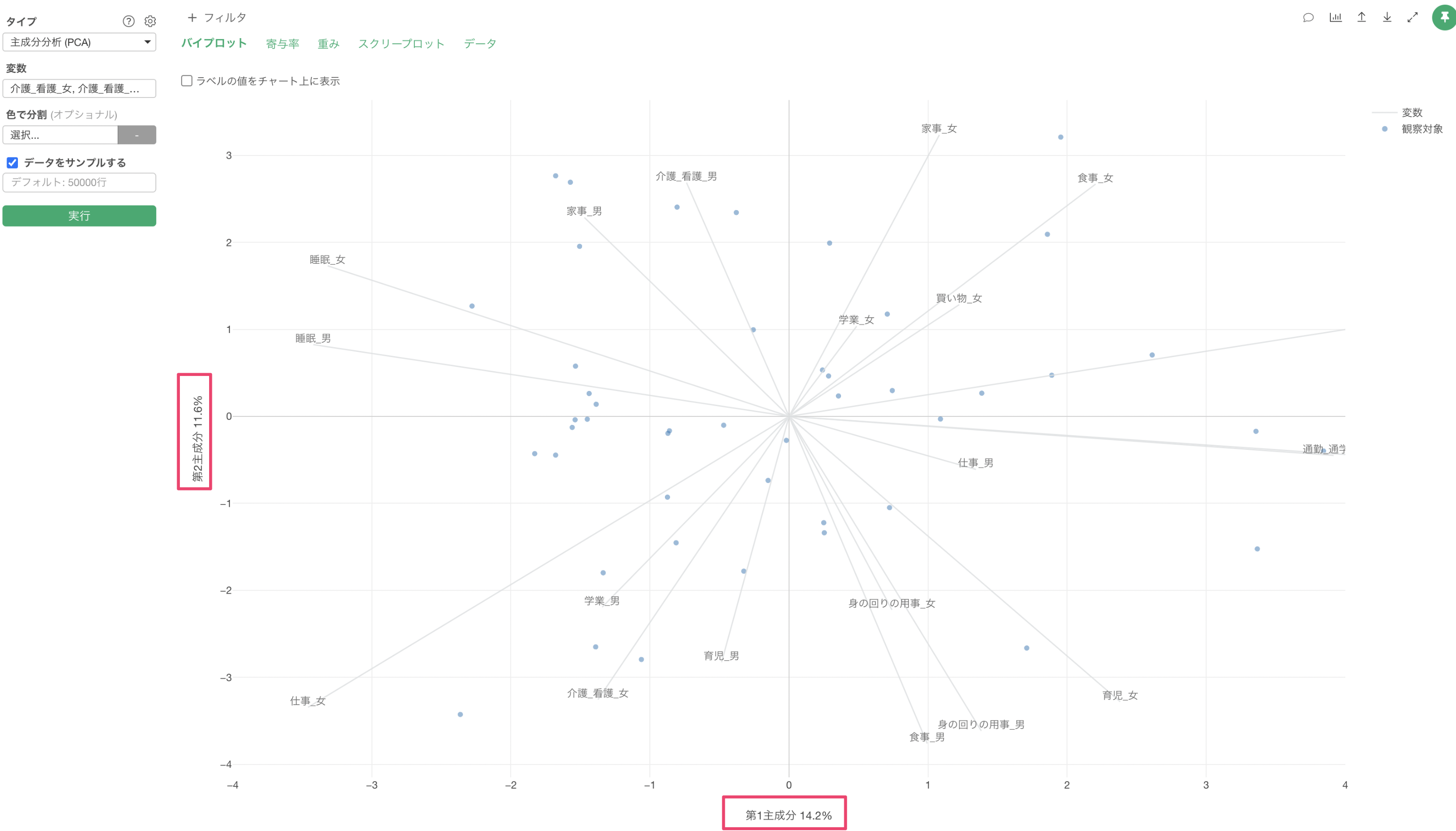
バイプロットのタブでは、それぞれの変数を2つの軸（第1主成分, 第2主成分）で表現しています。

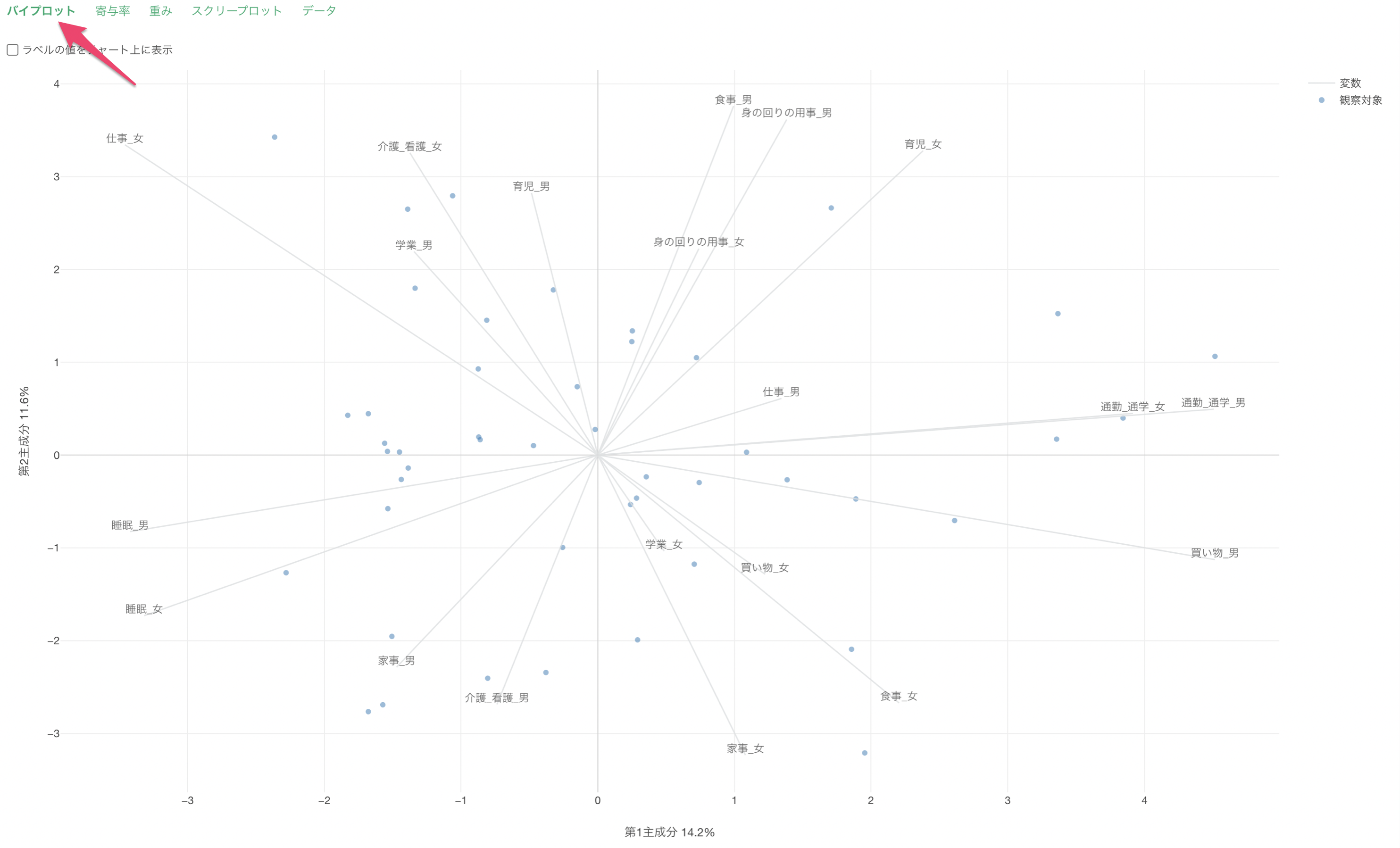
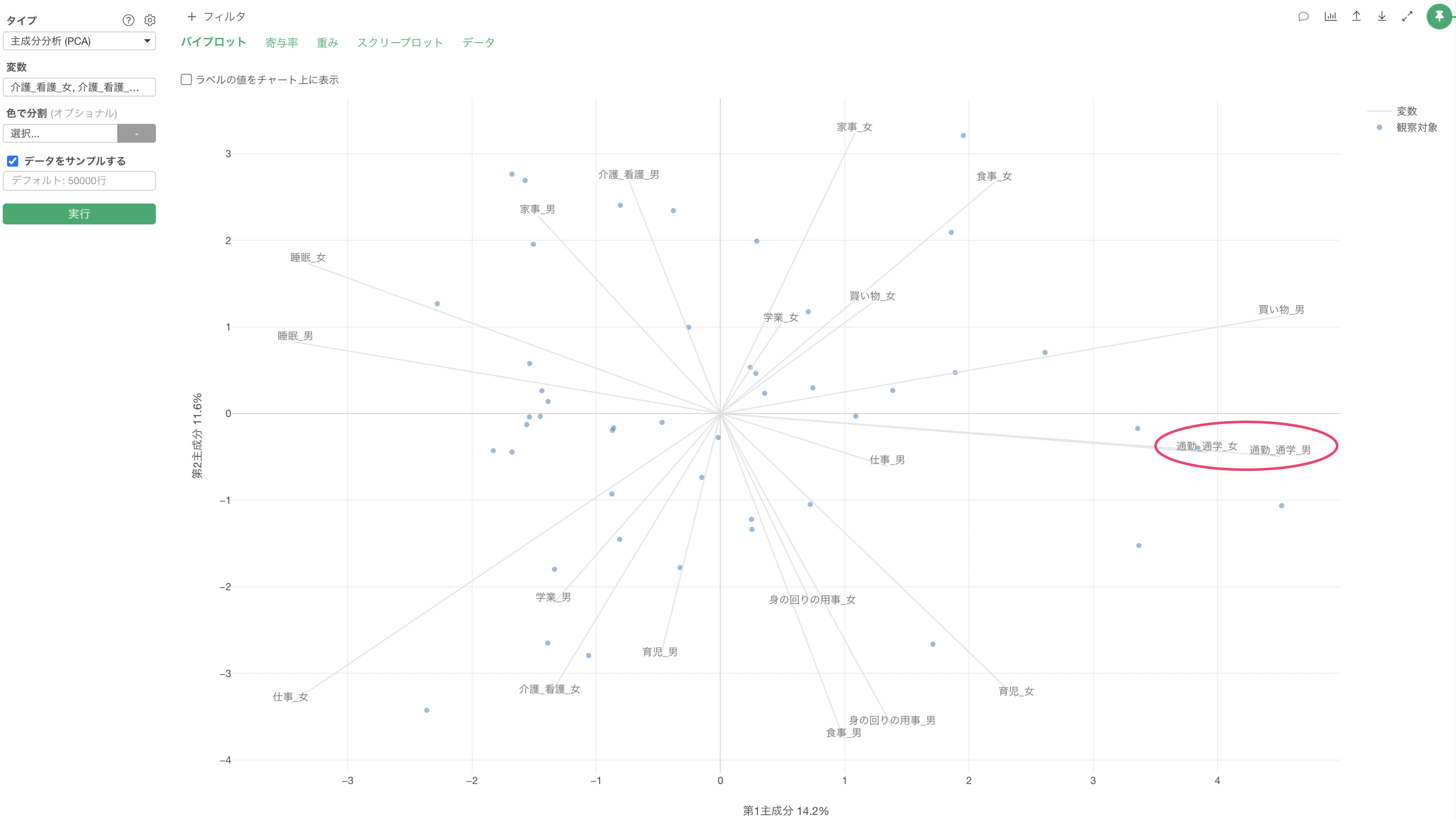
線はそれぞれの変数を、点はデータの1行を表します。変数の線が同じ方向に向いている場合は、それらの変数で相関関係があると判断できます。

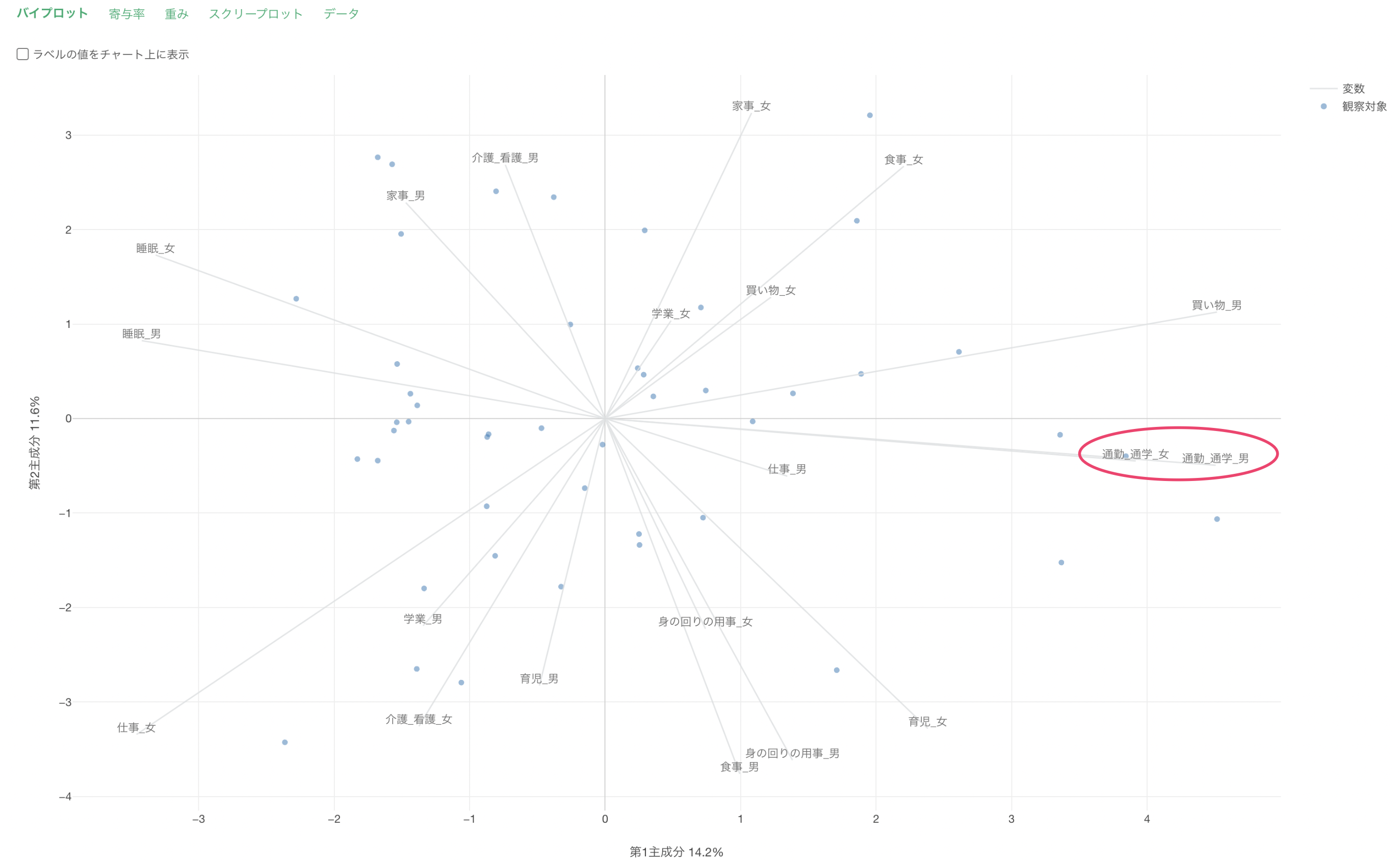
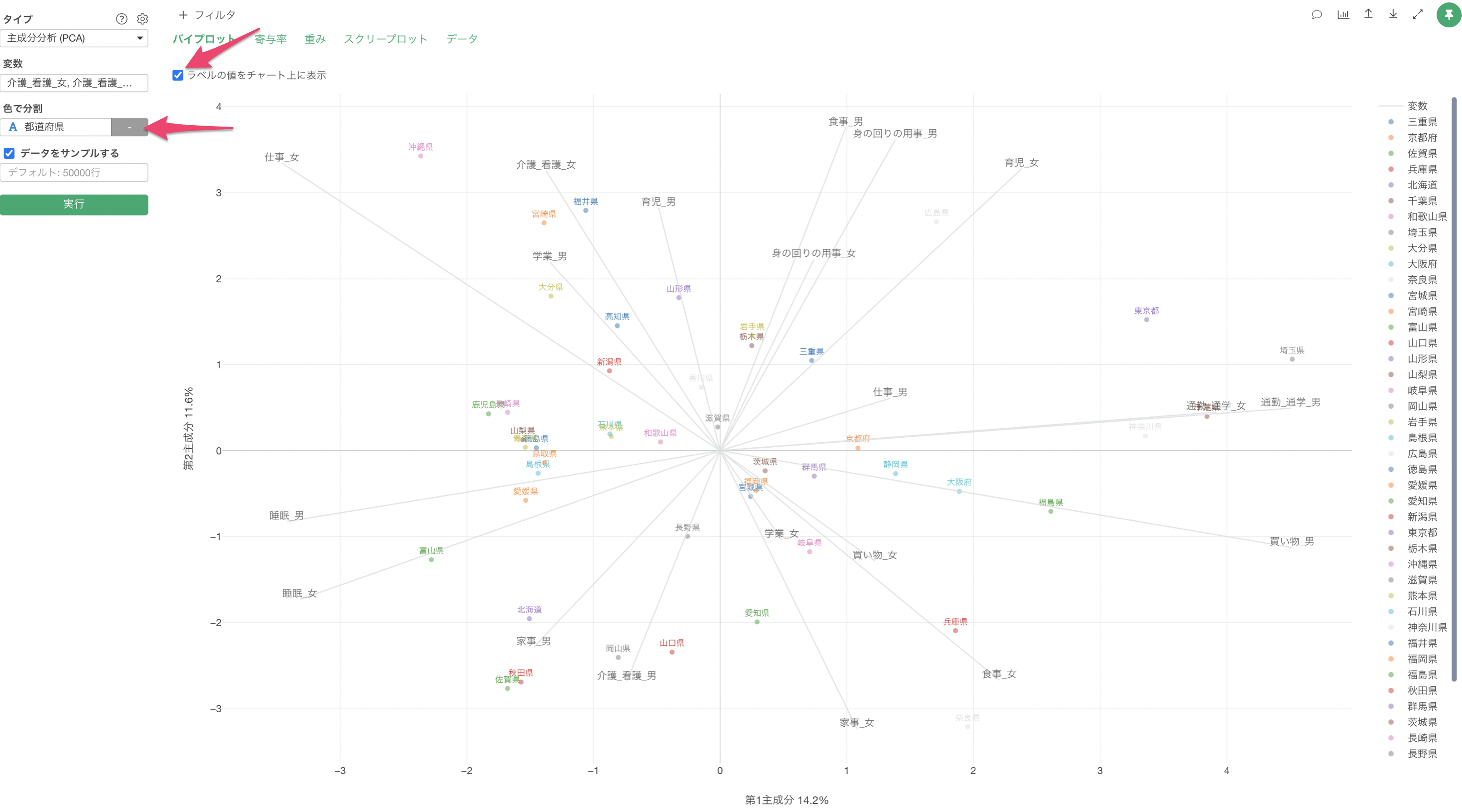
バイプロット上にラベルを表示したい場合は、「色で分割」に列を割り当て、「ラベルの値をチャート上に表示」にチェックをつけることで可能です。

下記は20列使用して主成分分析を実行したものとなりますが、第1主成分で14.2%、第2主成分で11.6%と2つ合わせて全ての変数のばらつきの25.8% を表現できていると捉えることができます。

残りの74.2%のデータのばらつきについては、第3主成分以降で説明がつくばらつきになっています。

また、それぞれの変数の軸線は主成分分析を実行した際の第1主成分、第2主成分のスコアをもとに位置が決まっています。

バイプロットの詳細については、こちらの「主成分分析（PCA）の紹介」のセミナーをご覧ください。

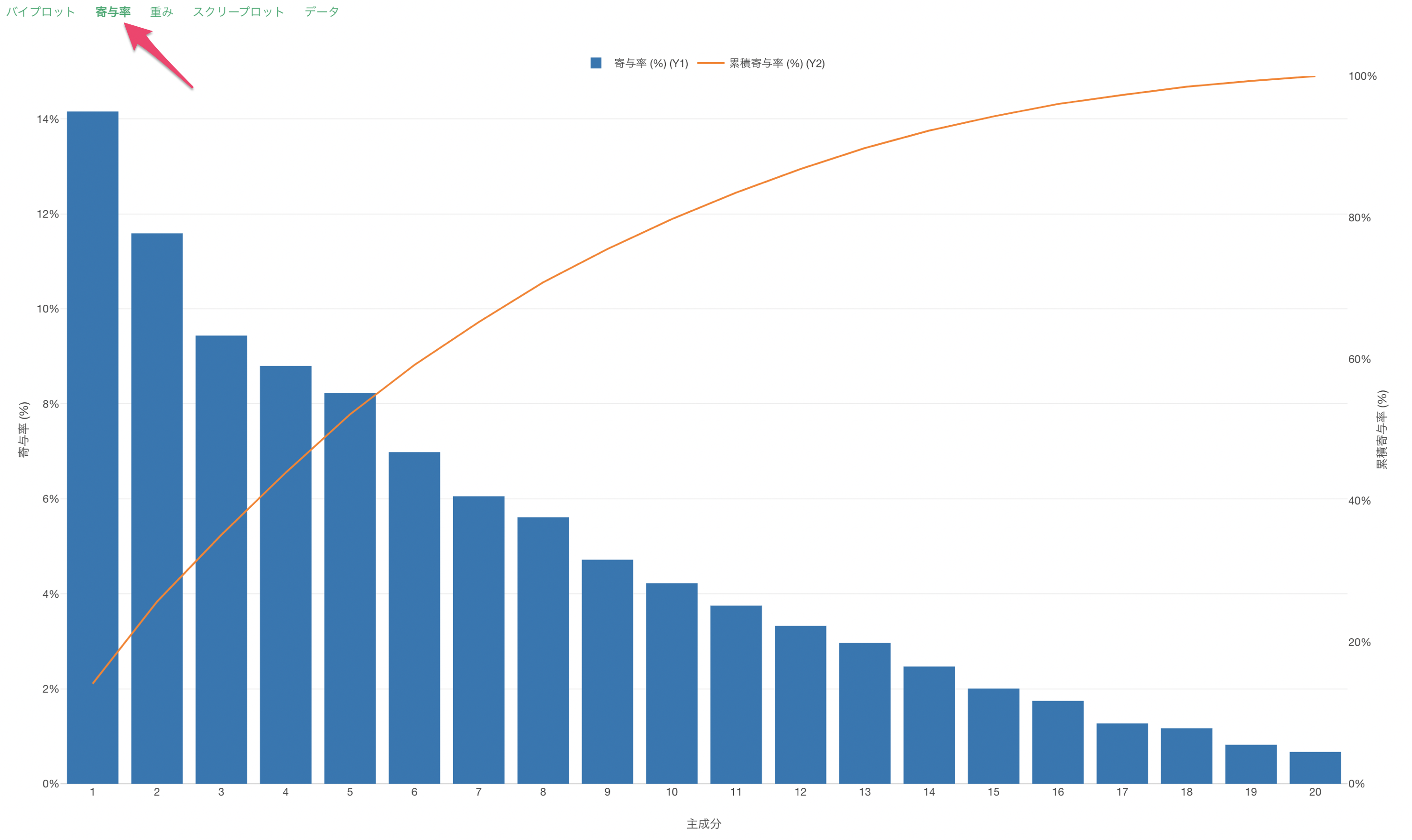
寄与率のタブでは、主成分分析で作られた軸である第1主成分、第2主成分によって元データの情報量（ばらつき）をどれだけ表現できるかを確認できます。

寄与率はそれぞれの主成分での情報量の表現できている割合で、累積寄与率はそれらの寄与率を足し上げて行った時にどれだけ表現できているのかがわかります。

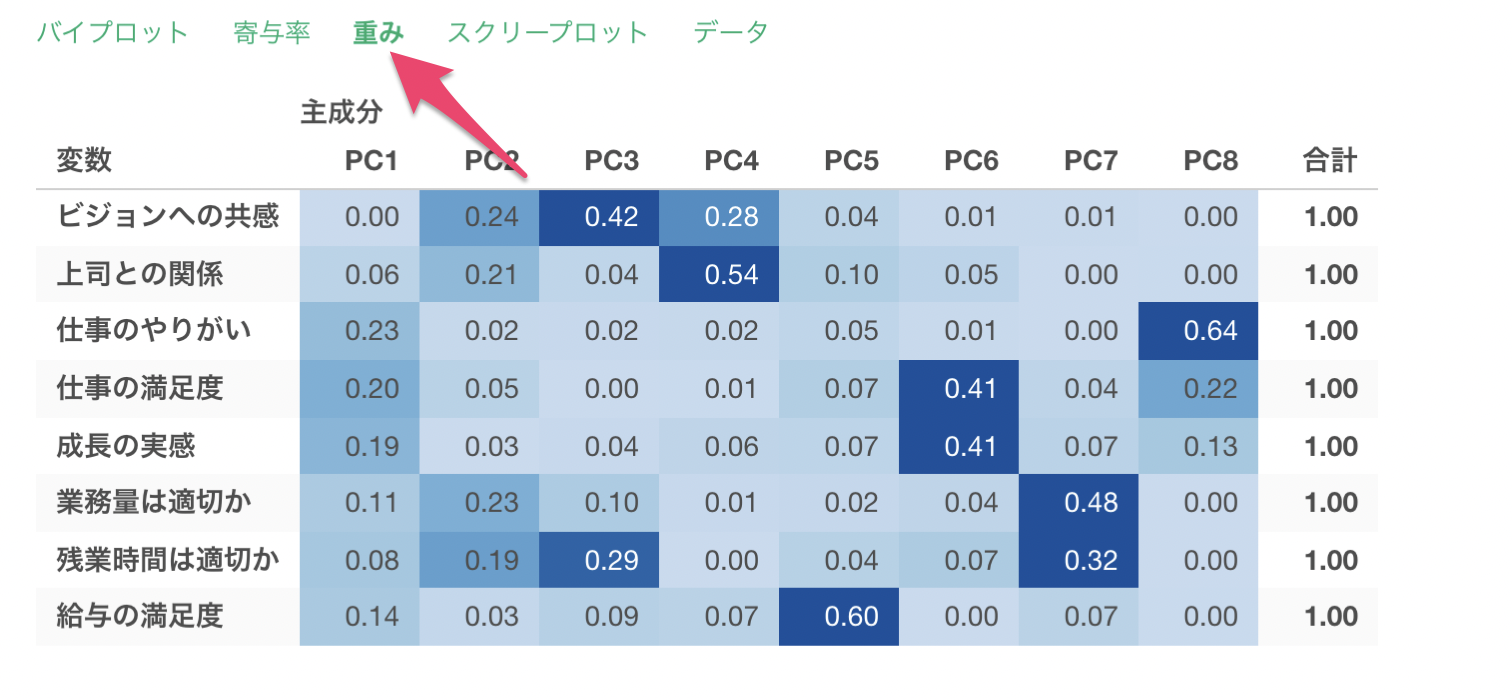
重みタブでは、それぞれの変数ごとに主成分の重みを確認することができます。

重みタブで表示されている指標は、「主成分負荷量」という指標で、主成分負荷量は該当変数が、各主成分にどの程度、寄与しているか（その主成分によって、どの程度その変数を説明できているのか）を表す指標です。

主成分分析に関する参考資料は下記をご覧ください。

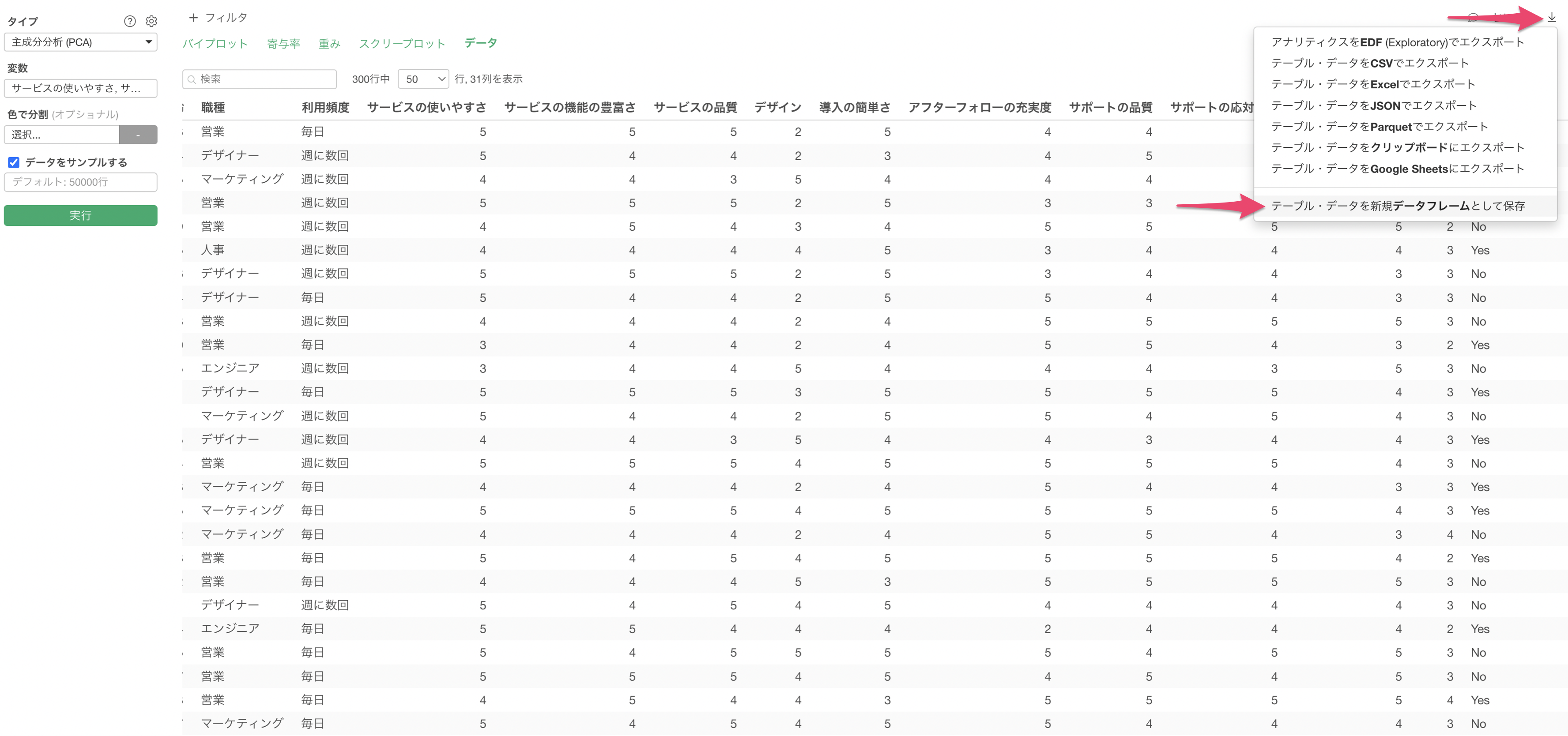
主成分分析のデータタブでは、元のデータに対して主成分スコアとしてPC1, PC2...が含まれています。

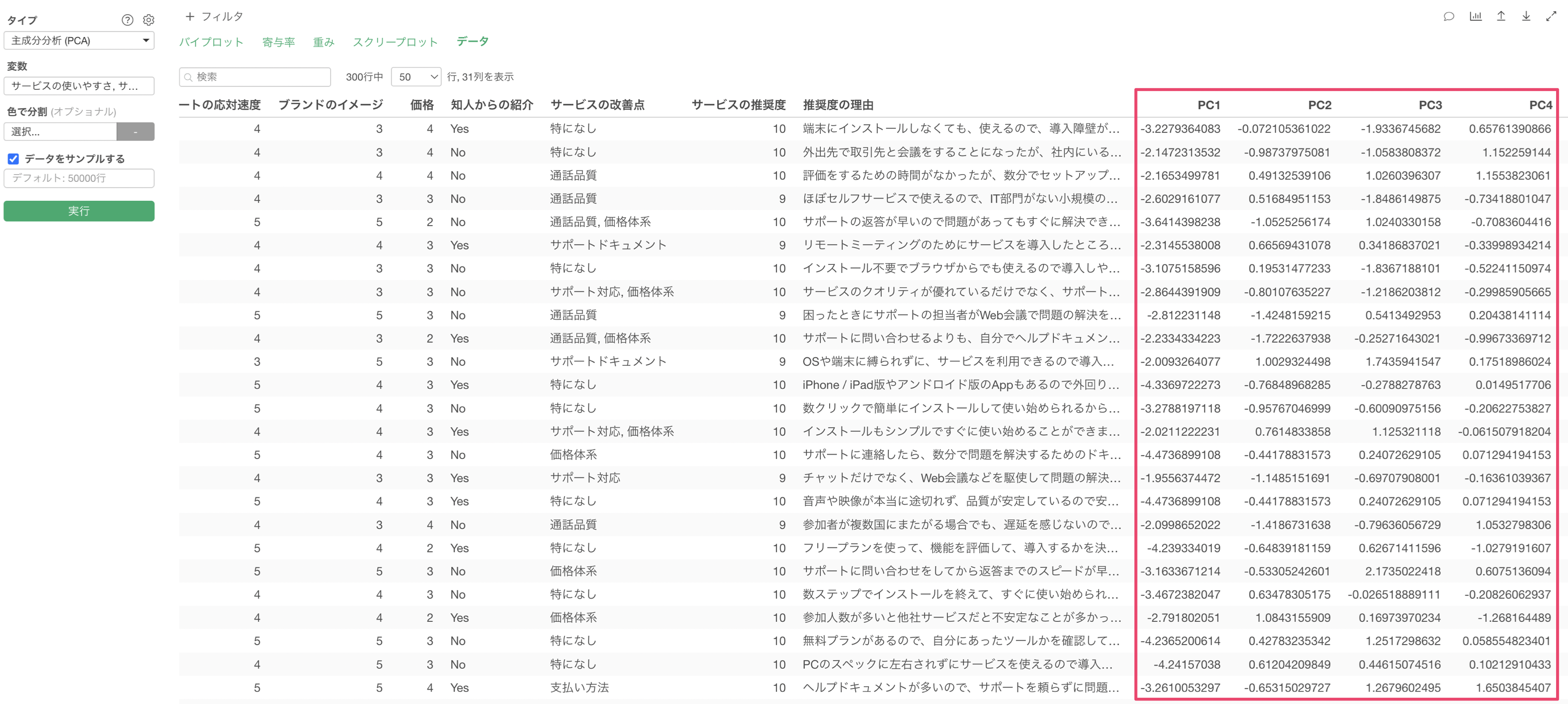
そのため、データタブからデータフレームとして保存をしていただくことで可能です。