NPSの信頼区間を計算する方法
NPS(ネット・プロモーター・スコア)は自社のサービスや製品に、顧客などがどれだけ価値を感じているかを測るためによく利用される指標です。
簡単かつ的確に顧客が感じている価値を測ることができるため、NPSは様々な企業で利用されていますが、サーベイの回答者数の大小に関わらず、1つの指標にまとめられてしまう、という問題があります。
そこで、こちらのノートではNPSの信頼区間を計算・可視化する方法を紹介します。
NPSとその計算方法や信頼区間の詳細は以下よりご確認ください。
NPSの信頼区間の計算式
NPSの「95%信頼区間」は以下の式から計算できます。

サンプル数はNPSサーベイの回答者数を表すため、「NPSの分散」がわかれば、信頼区間を計算できるわけです。
変数のタイプと離散型変数の分散
ところで、NPSのような変数(色々な値を取り得るもの)には、以下の2つのタイプがあります。
- 離散型
- 連続型
例えばサイコロを振ったときに出る目は、1と2の間の1.5という値をとることはなく、とびとびの数値で表されるため、「離散型」の変数です。
一方で身長や体重は170.1cm、170.2cmのように、連続的な数値で表されるため、「連続型」の変数です。
NPSは回答者数が決まると、取り得るNPSのスコアが決まり、連続的な数値をとることはないため、「離散型」の変数です。
そして離散型の変数の「分散」は以下の計算式を使って、「期待値(平均して期待できる値。平均値の一種)」をもとに求めることが可能です。

上記の計算式で使われている「確率」や「実現値」については、この後詳しく説明します。
離散型変数の期待値
NPSの期待値を計算する前に、まずは簡単な例を使って離散型の変数の期待値を計算する方法を紹介します。
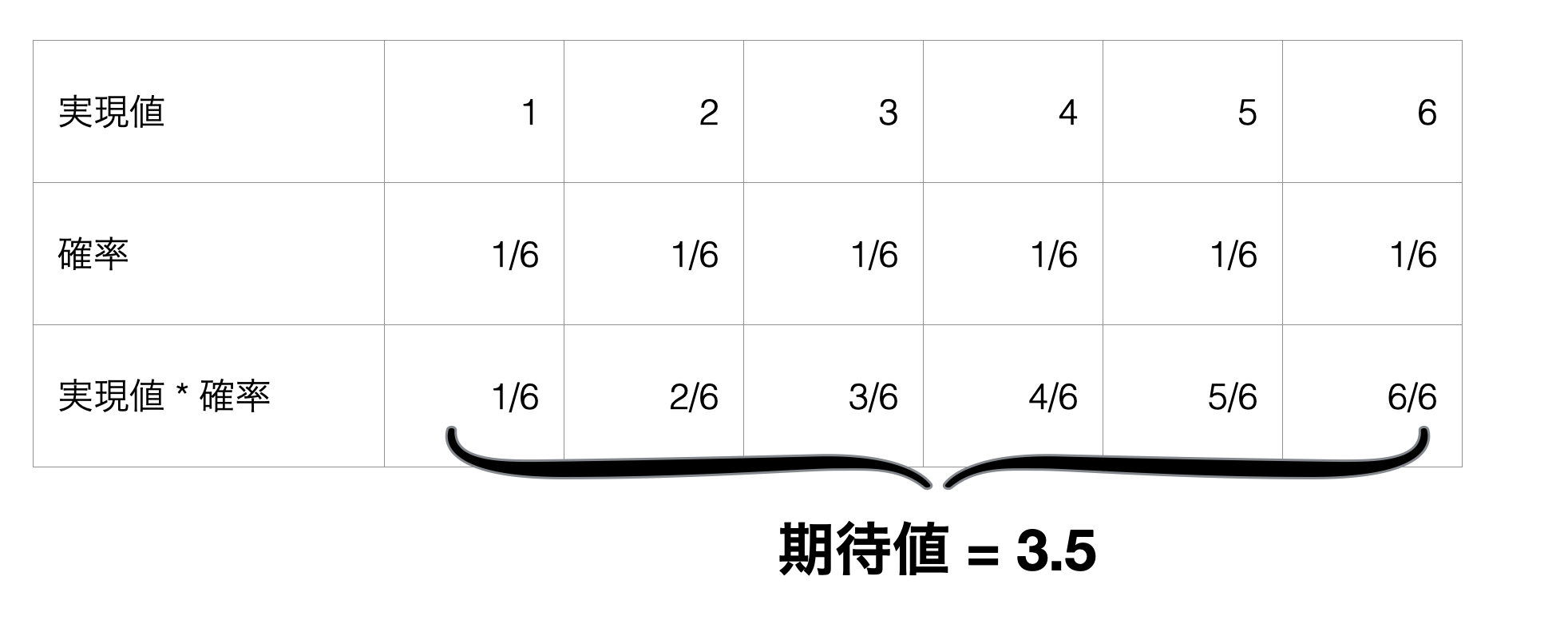
今回はサイコロを1回振ったときに出る目の数の期待値を例に考えてみます。
サイコロには1から6の目があり、それぞれの目が出る可能性は等しく1/6です。
期待値は以下のように全ての実現値(期待される結果、今回で言うサイコロを振ったときに出る目の数)に、その実現値を得られる確率を掛けて求められる値を全て足した指標です。

上記の計算を表形式でまとめたものが以下になりますが、サイコロを1回振ったときに出る目の数の期待値は3.5になるわけです。
NPSの期待値
ここからは、NPSの期待値の考え方を紹介します。
NPSは以下のように、プロモーターからデトラクターの割合を引いた指標で、パッシブの割合はNPSの計算結果に影響を与えません。
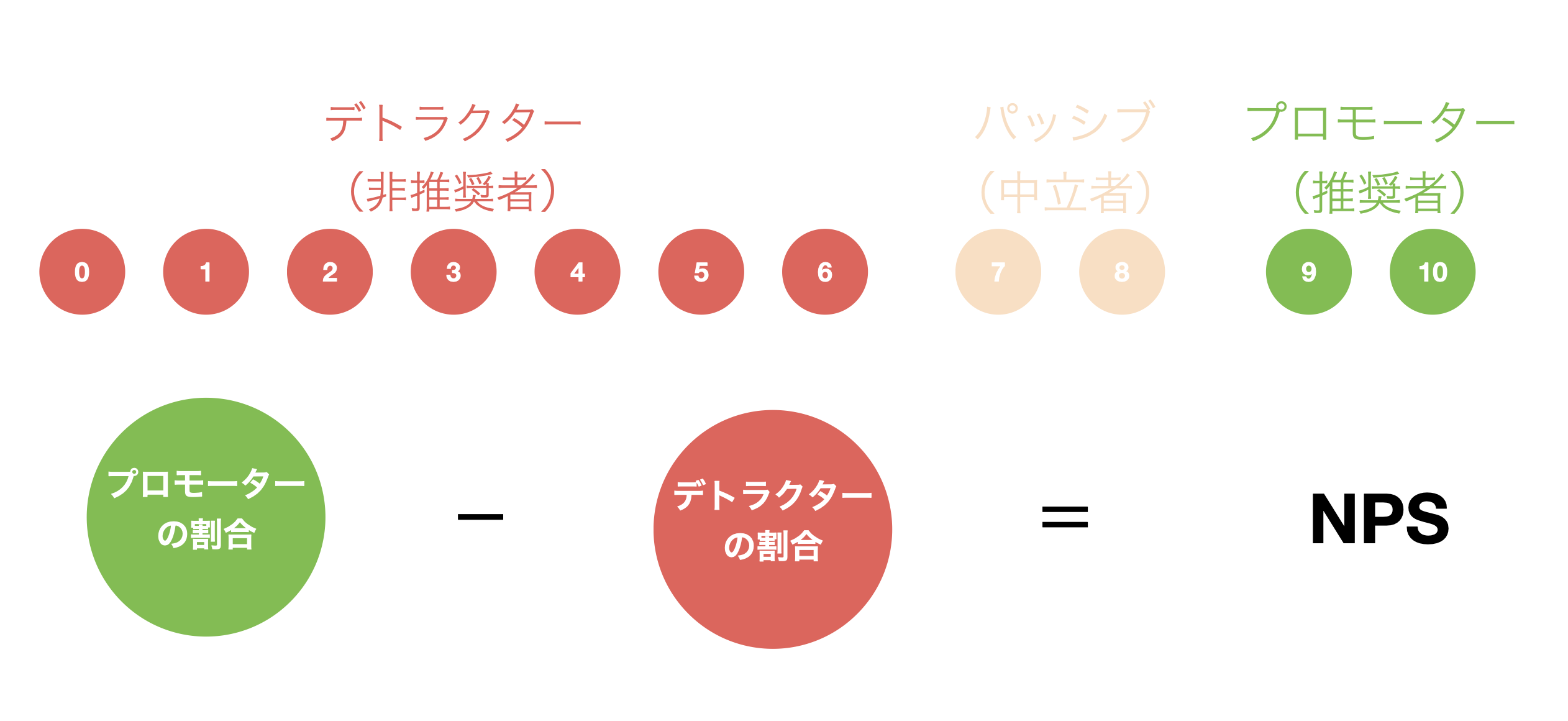
そのため、NPSにはプロモーターが1人増えると1スコア分増え、デトラクターの場合は1スコア分減る特徴があると捉えられます。
また、パッシブの場合はスコアが変わらないため、各々の回答(グループ)における実現値は以下のように捉えられます。
- デトラクター: -1
- パッシブ: 0
- プロモーター: +1
さらに各グループの出現確率は、それぞれのグループの割合です。す。
上記を踏まえて、NPSのサーベイに参加した人数が100人、プロモーターが80人、デトラクターが10人だった場合のNPSの期待値を先程のテーブルを使って計算すると、NPSの期待値は0.7であることがわかります。

上記の例におけるNPSは70%(0.7)です。

このようにNPSの期待値はNPSそのものを表していることになるわけです。
NPSの分散
これまでの説明からNPSサーベイにおける実現値は以下となり、
- デトラクター: -1
- パッシブ: 0
- プロモーター: +1
期待値はNPSの値そのものであることがわかっています。
前述した分散を求める計算式にそれらをあてはめると、以下のように計算式をアップデートできます。
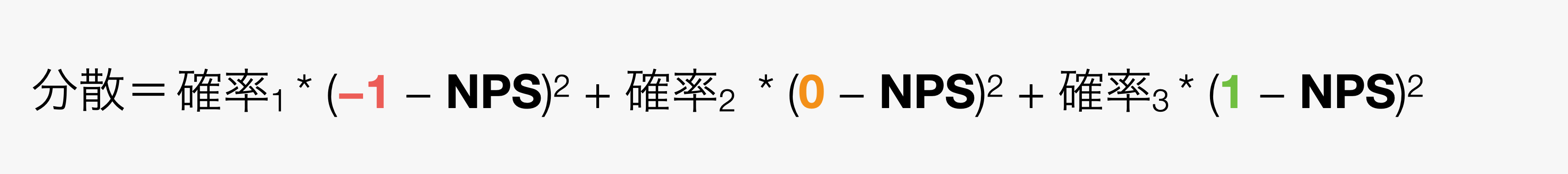
さらに、各実現値における確率は各カテゴリーの割合になるため、分散の計算式は、さらに以下のようにアップデートできます。

この計算式を先程の例にあてはめて考えると、分散は0.41と計算できます。
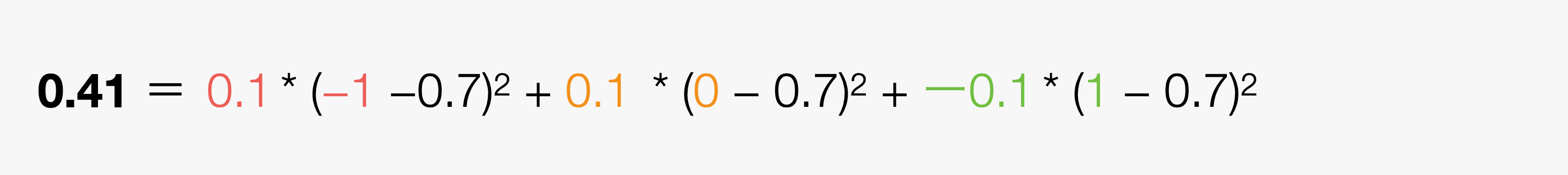
このとき、NPSには小数点表記のスコアを利用する点に注意してください。
NPSの信頼区間の計算
分散を求めることができたら、NPSの95%信頼区間を求める計算式に、分散やサンプルの情報をあてはめます。

先程の例におけるNPSは「0.7(70)」、分散は「0.41」、サンプル数(回答者数)は「100」になるため、NPSの95%信頼区間は、以下を計算することで求められるわけです。

Exploratoryを使ったNPSの信頼区間の計算
ここからは、Exploratoryを使ってNPSの信頼区間を計算・可視化していきます。
今回は1行が1つのセミナーを表し、列にはセミナー名、回答者数、各カテゴリーの割合、NPSのスコアの情報を持つNPSサーベイの集計データを利用します。

データはこちらのページからダウンロードできます。Macをお使いの方は「CSV-UTF8」を、Windowsをお使いの方は「CSV - Shift-JIS」をダウンロードしてください。
今回のような集計データを、NPSサーベイの回答データからつくりたい方は以下をご参考ください。
- NPSの計算 - リンク
データをインポートしたら、NPSの信頼区間の計算式を思い出してみます。

今回のデータにはNPSやサンプル数(回答者数)の情報があるので、「分散」を計算するだけで信頼区間の計算が可能です。

NPSの分散の計算式は以下となるので、こちらの計算式をもとに、NPSの信頼区間を求めていきます。

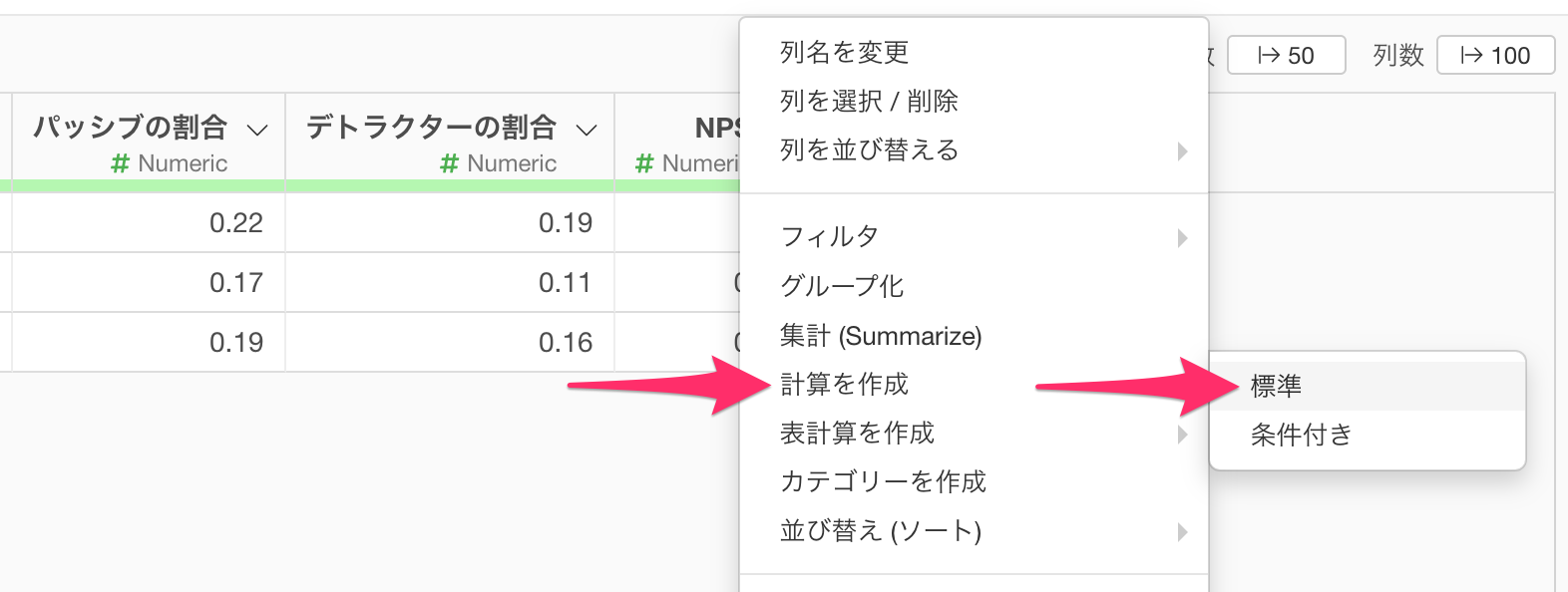
「NPS」の列ヘッダーメニューから「計算を作成」の「標準」を選択します。
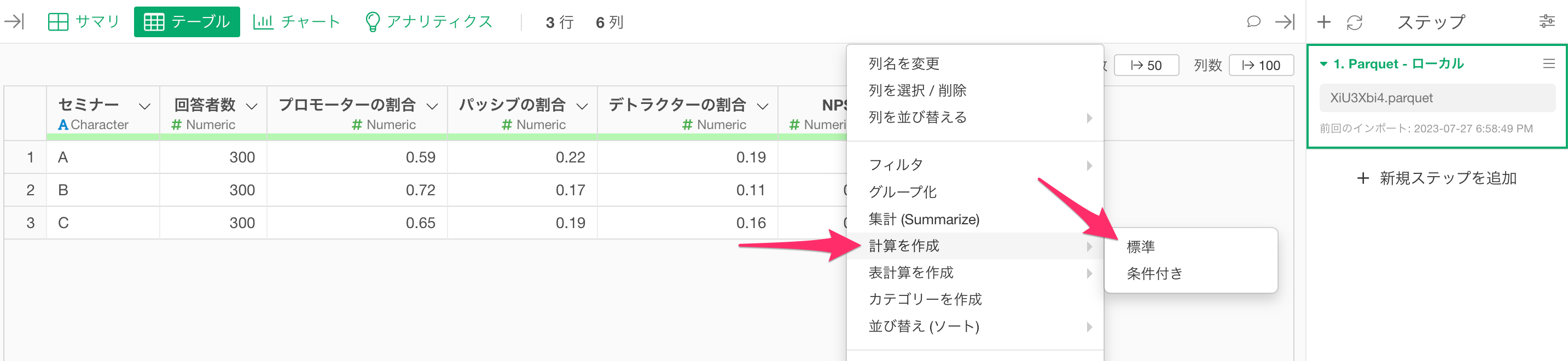
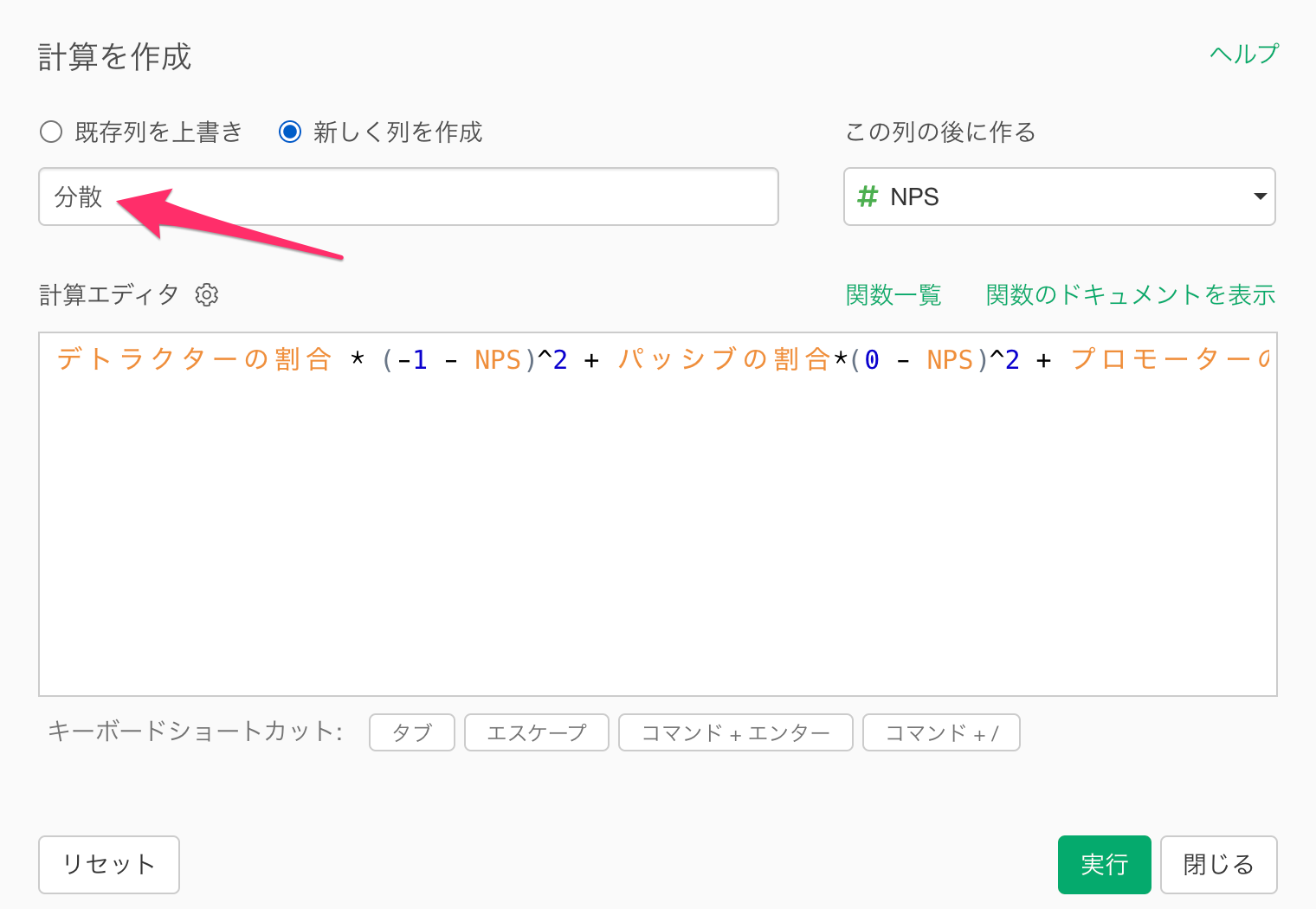
「計算を作成」のダイアログが表示されたら、計算エディタにNPSの分散を計算する以下の計算式を入力します。
デトラクターの割合 * (-1 - NPS)^2 + パッシブの割合 * (0 - NPS)^2 + プロモーターの割合 * (1 - NPS)^2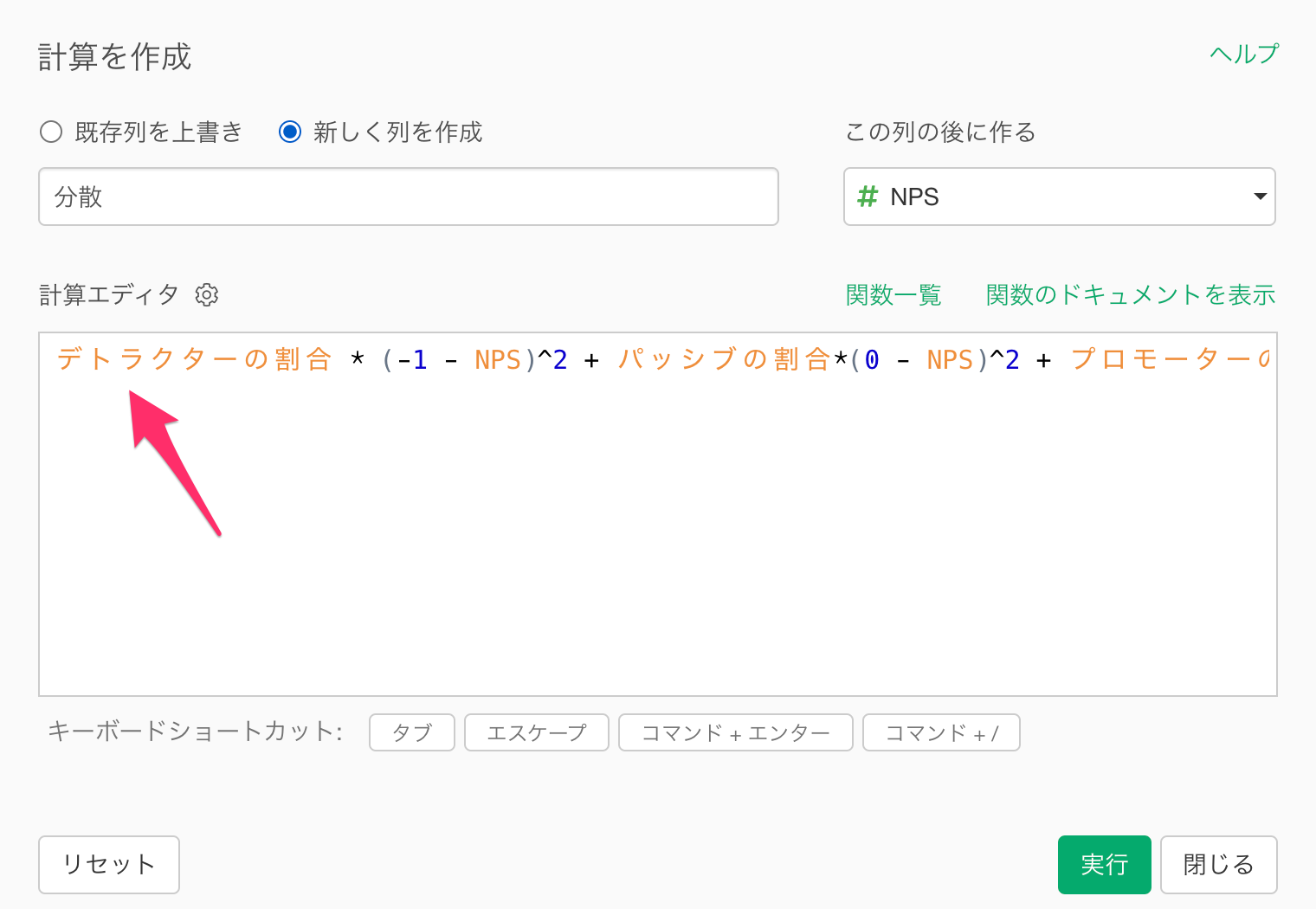
なお^2は二乗を表します。
計算エディタに上記の計算式を入力したら、新しい列名に「分散」を指定して実行します。
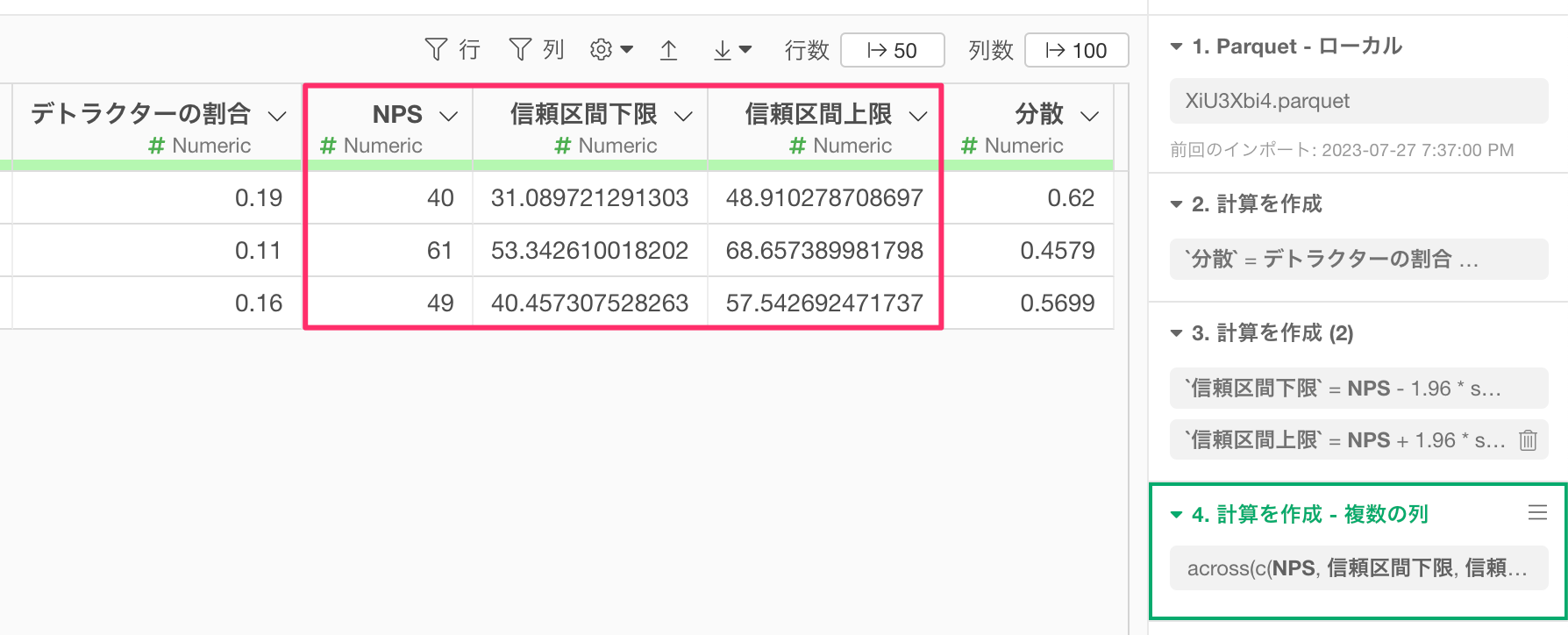
これでNPSの分散を求めることができました。
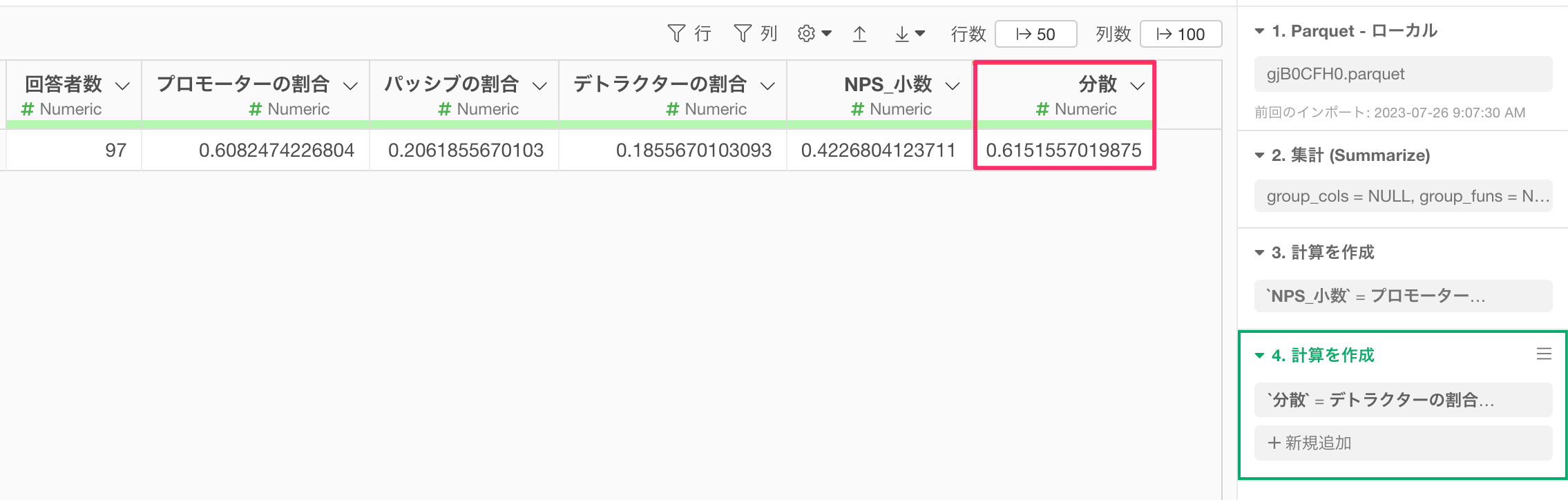
後は、求めた分散の情報を使って信頼区間を計算するだけです。
まずは、信頼区間の上限を計算するために、「NPS」の列ヘッダーメニューから「計算を作成」の「標準」を選択します。
「計算を作成」のダイアログが表示されたら、NPSの信頼区間の下限を計算する以下の計算式を入力します。
NPS - 1.96 * sqrt(分散 / 回答者数)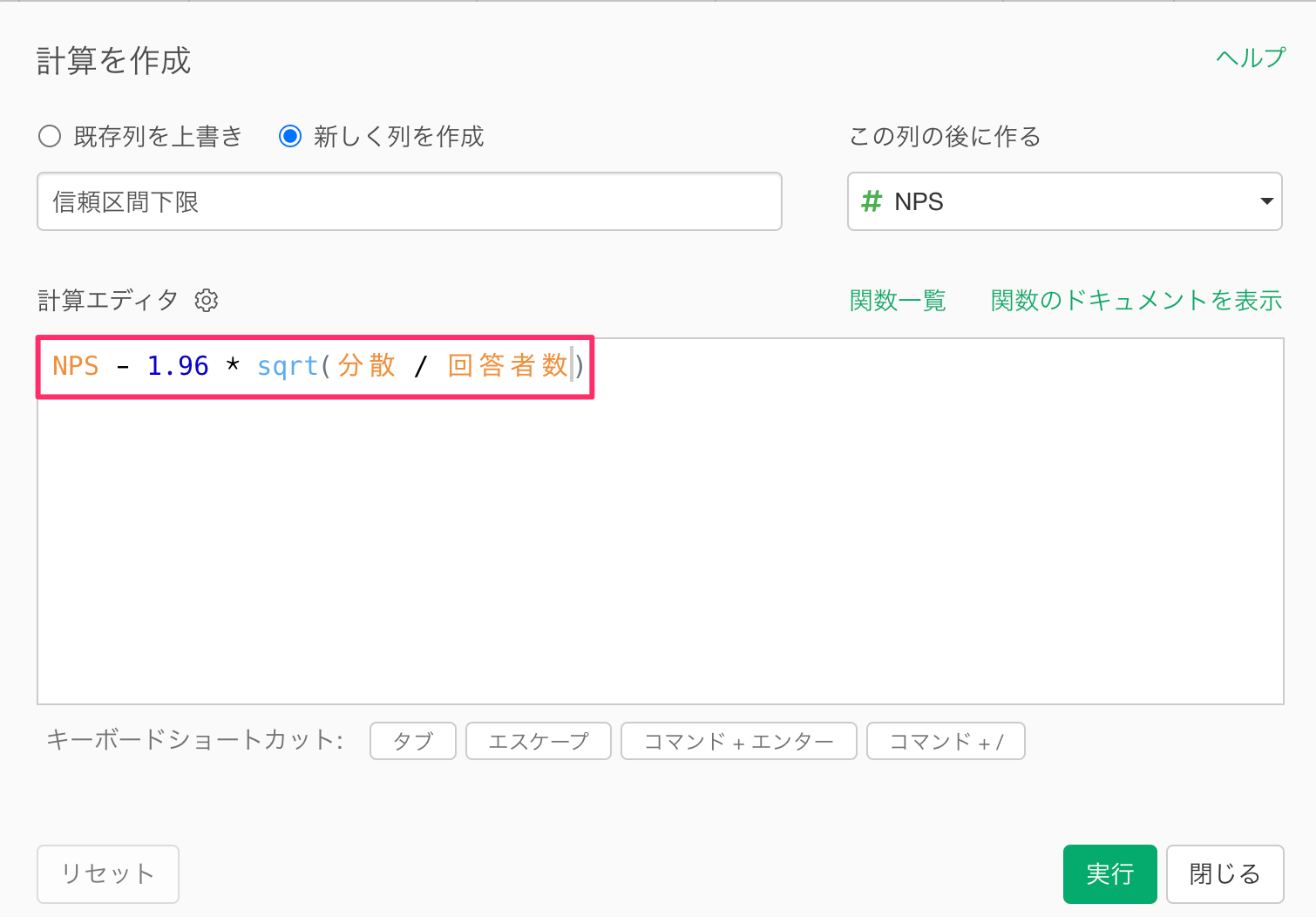
なお、sqrt関数は、引数の平方根(ルート)を計算する関数です。
計算エディタに上記の計算式を入力したら、新しい列名に「信頼区間下限」を指定して、実行します。
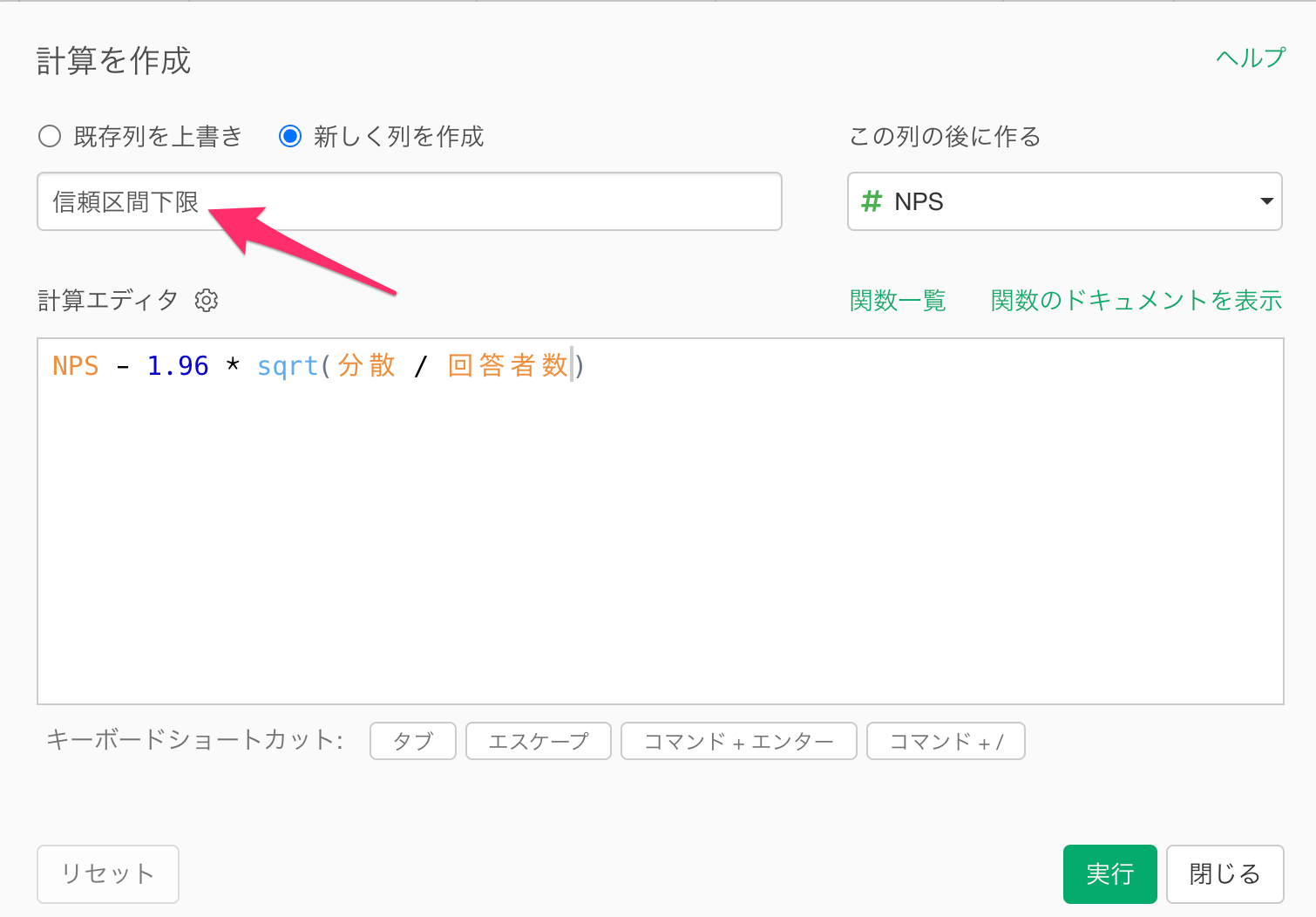
信頼区間の下限値を計算することができました。
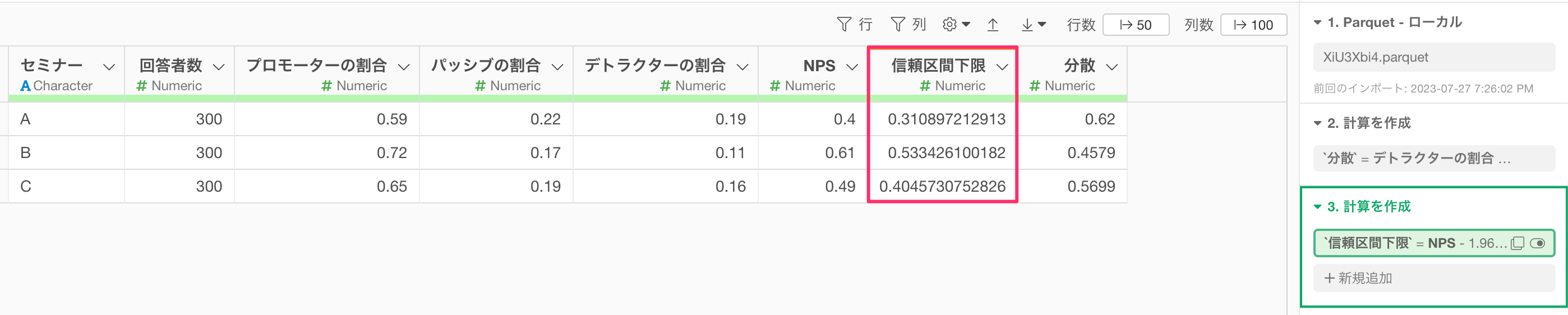
続いて、信頼区間の下限値を計算したステップのトークンの複製ボタンをクリックします。
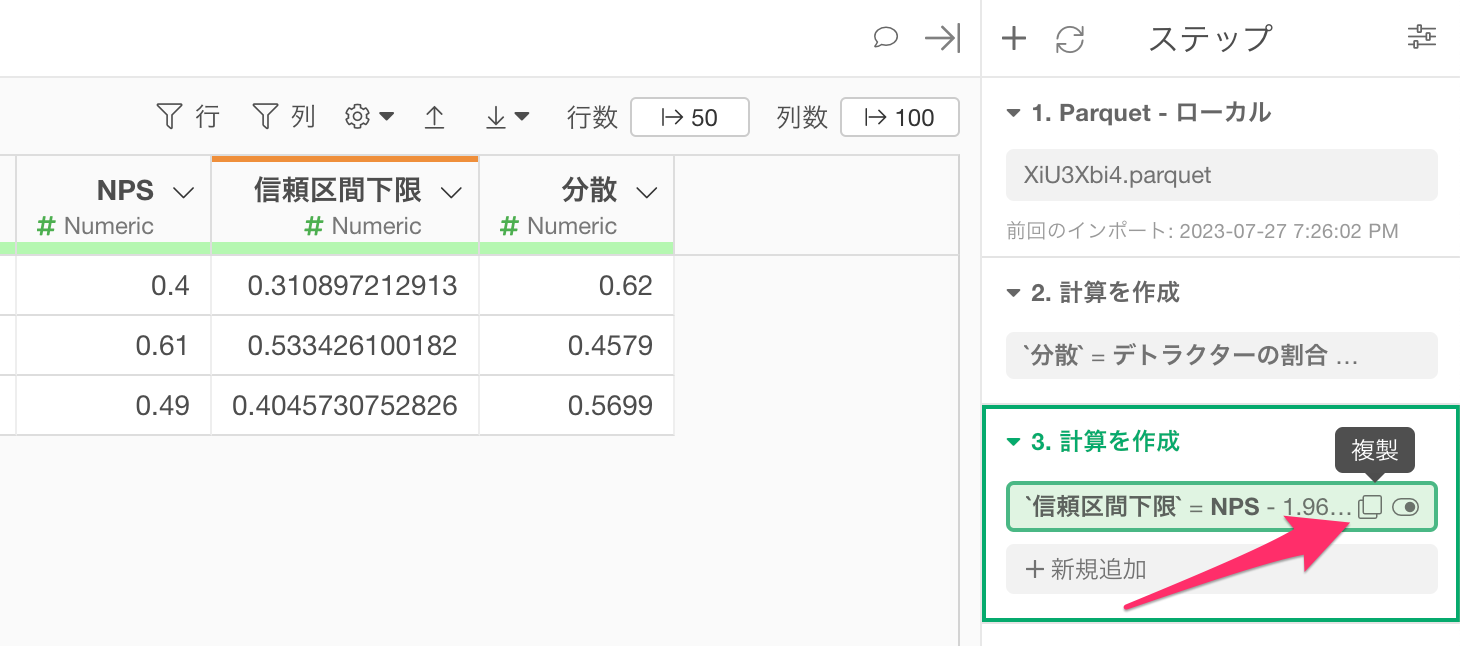
すると、信頼区間の下限値を計算したステップのトークンの複製されるので、トークンをクリックします。
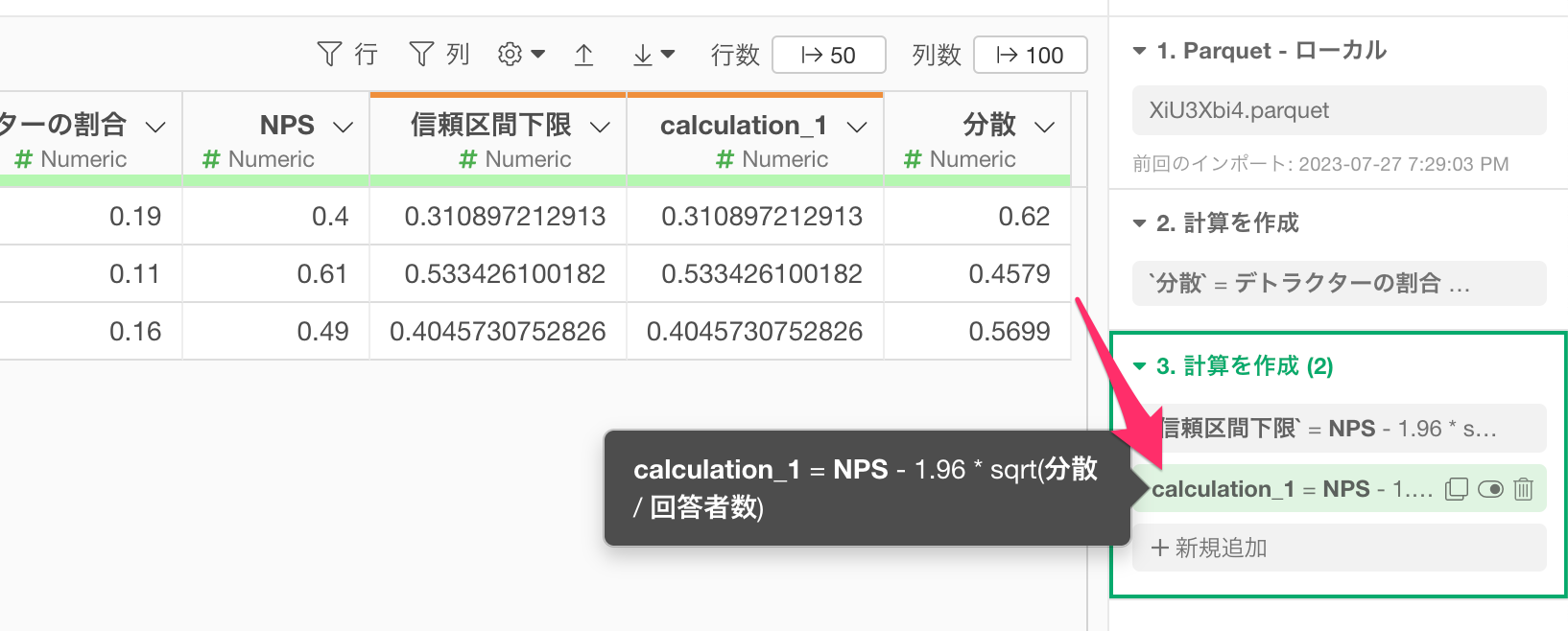
すると、複製したトークンのダイアログが表示されるので、計算エディタの内容を下記にアップデートし、新しい列名に「信頼区間上限」を指定して、実行します。
NPS + 1.96 * sqrt(分散 / 回答者数)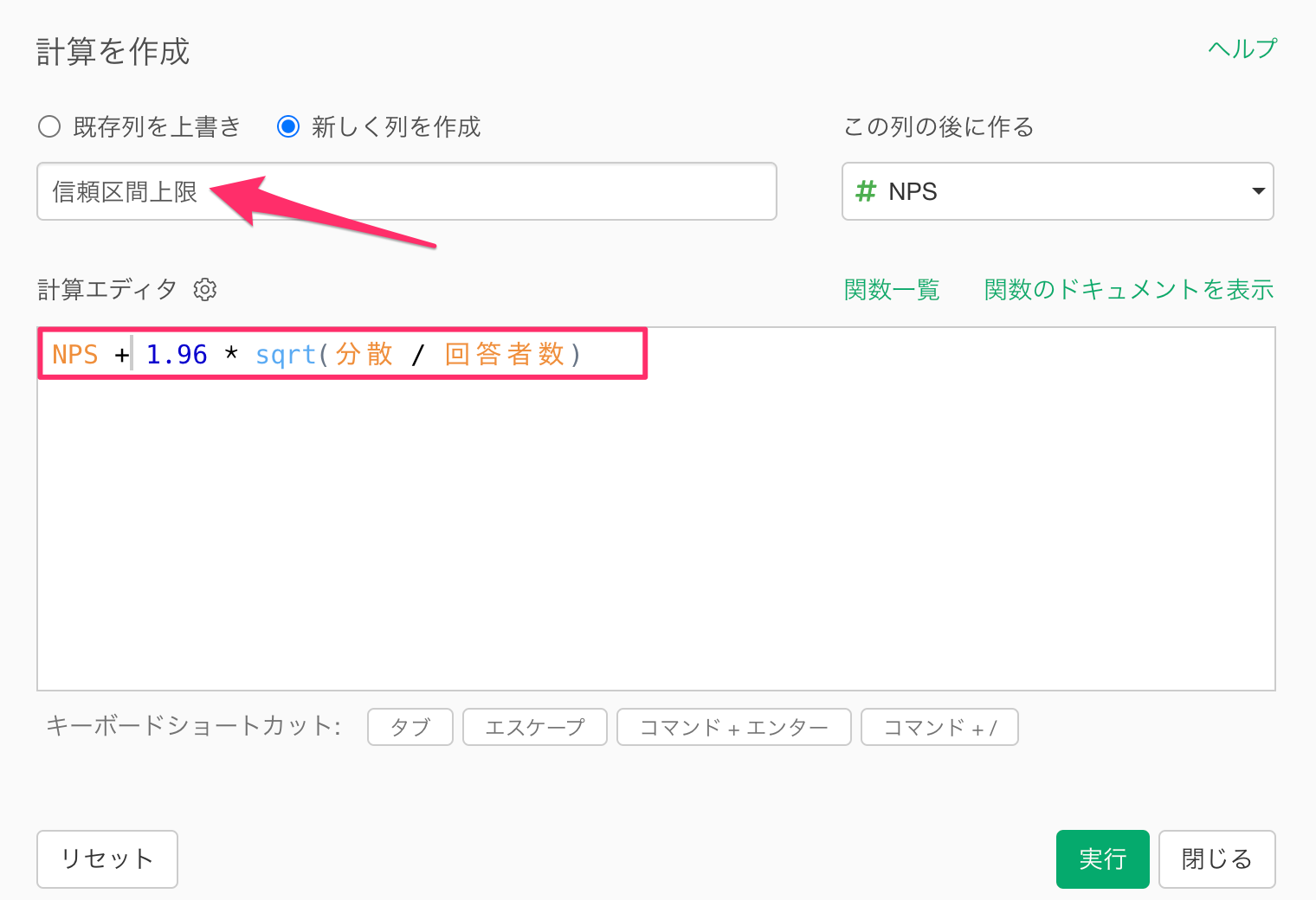
信頼区間の上限値を計算することができました。
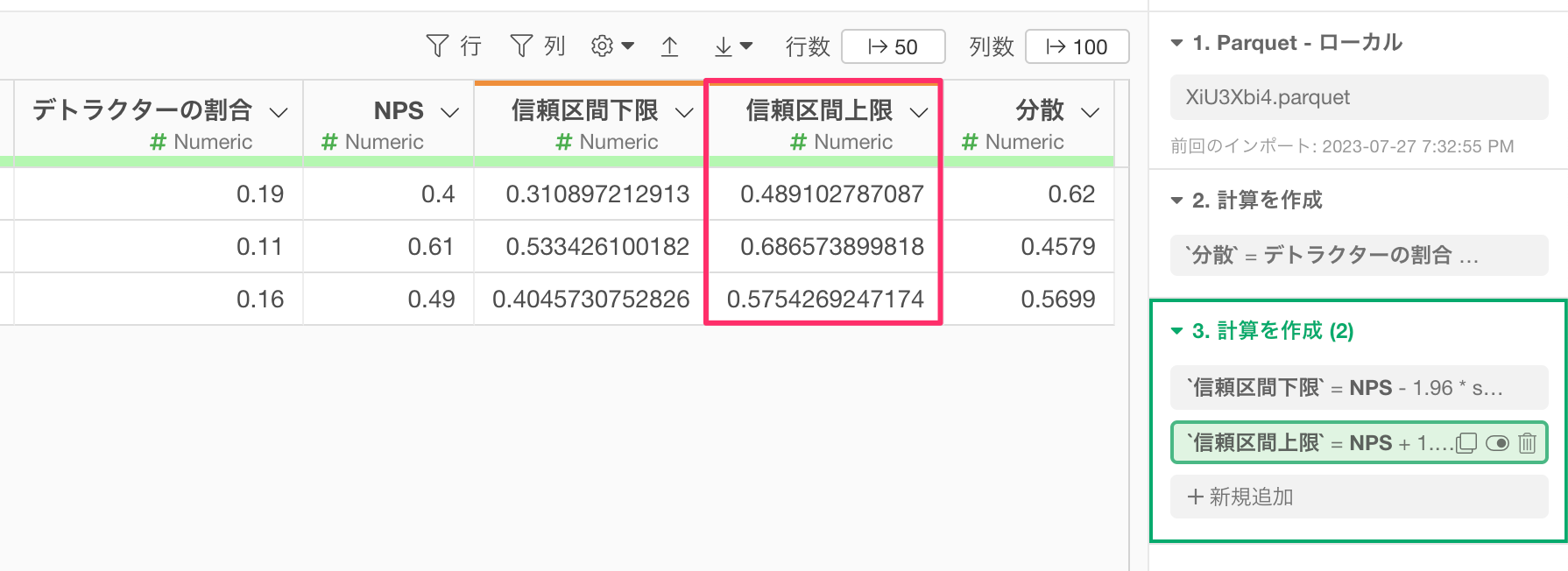
最後に、NPSと信頼区間の上限・下限の値に100を掛けてNPSのスコアに変換していきます。
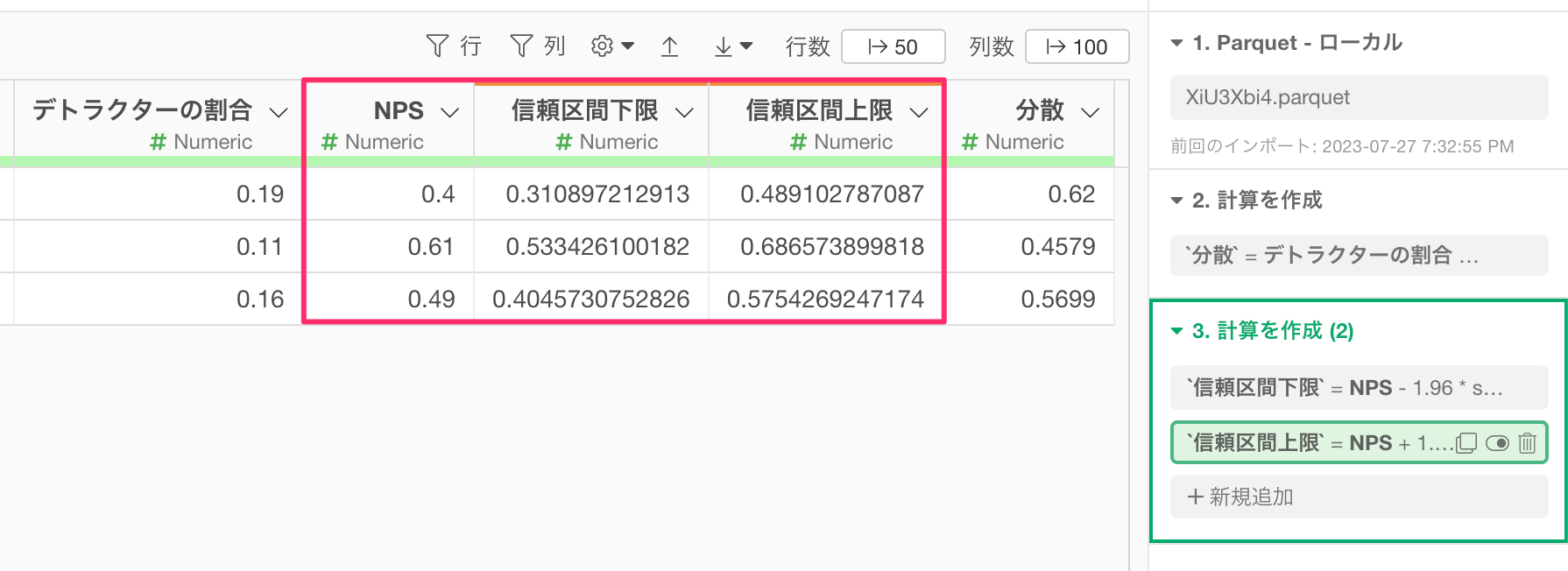
Shiftキーを押しながら、「NPS」と「信頼区間上限」の列を選択し、列ヘッダーメニューから「計算を作成-複数の列」の「標準」を選択します。
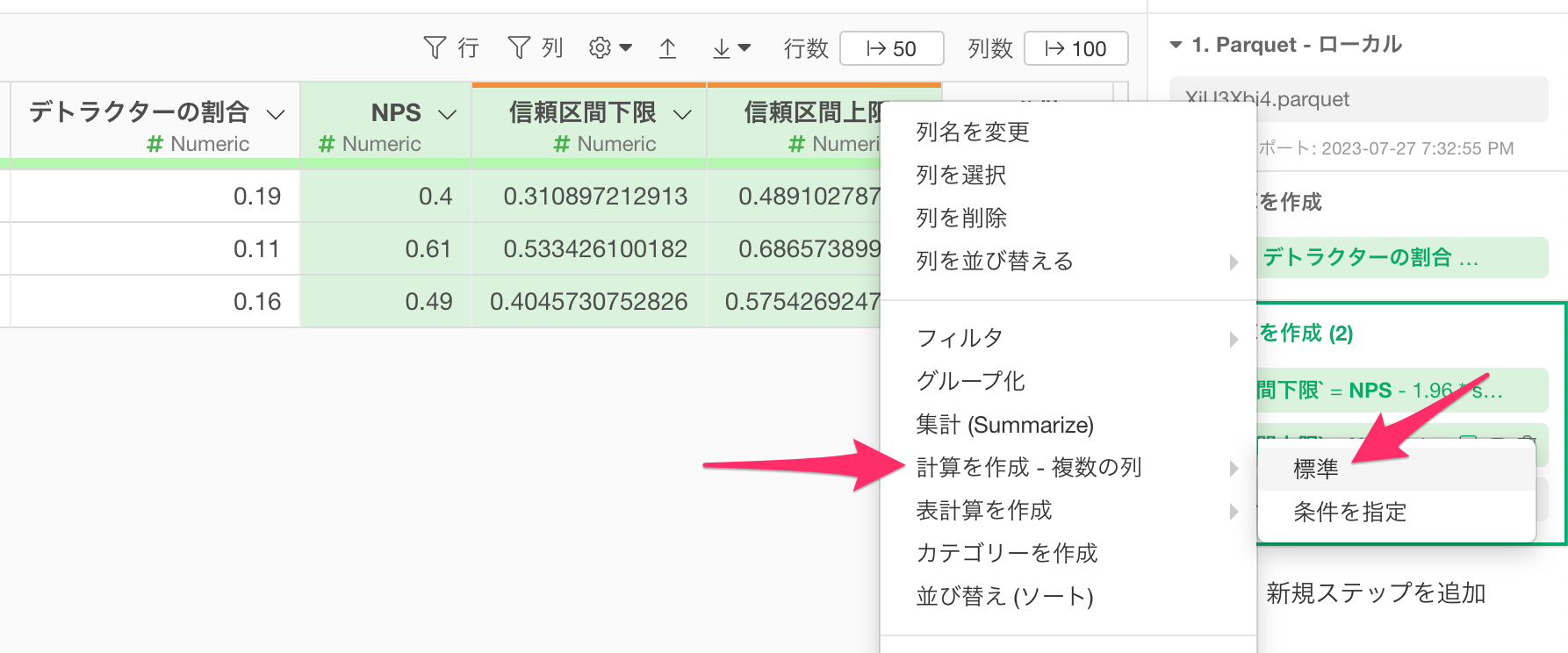
「計算を作成」のダイアログが表示されたら、計算エディタに以下の数式を入力し、実行します。
. * 100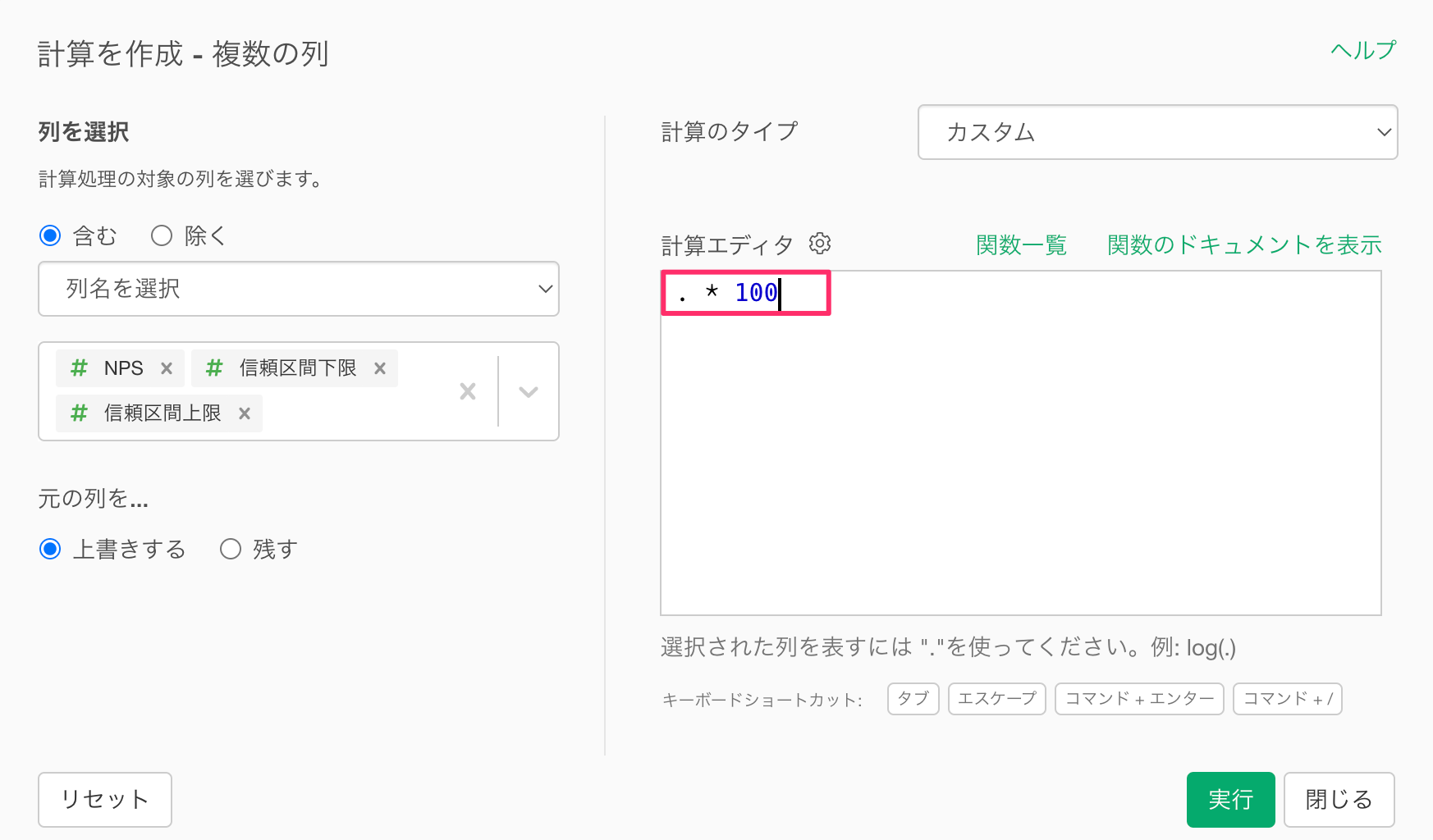
なお、.は選択された列を表しているので、前述の計算式は、選択した列に100を掛けるという計算になるわけです。
これでNPSと信頼区間を計算できました。
信頼区間の可視化
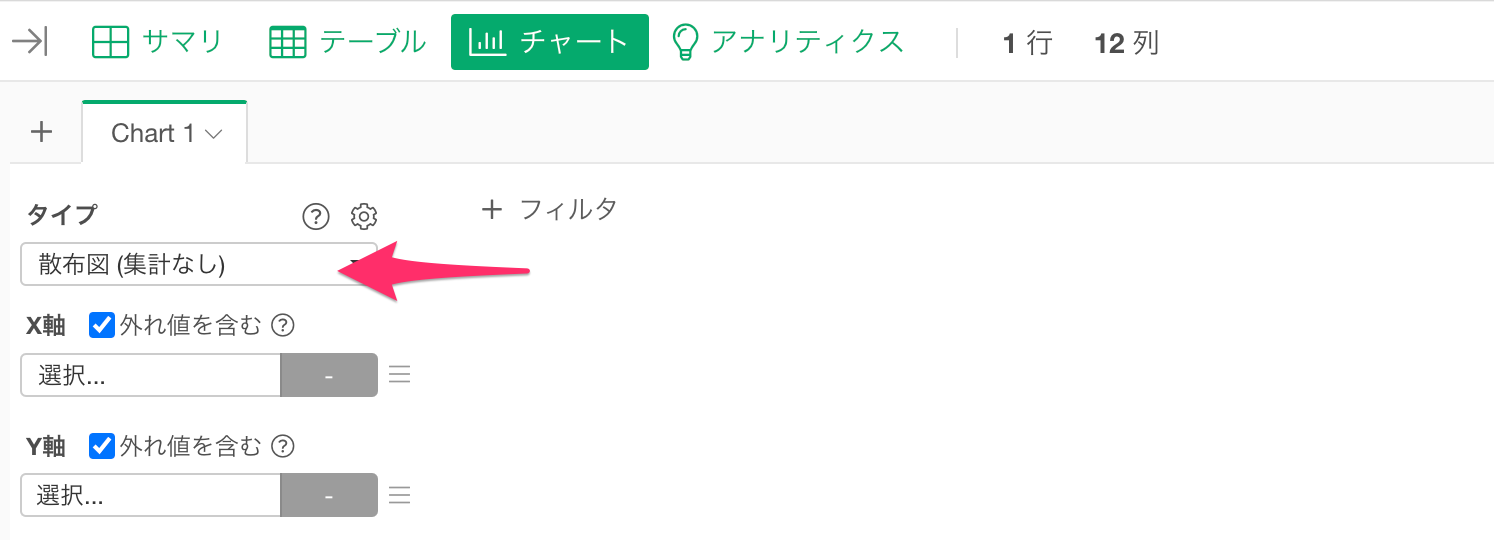
今回のデータのようにカテゴリーや日付の列があるときには、計算したNPSの信頼区間を可視化することも可能です。

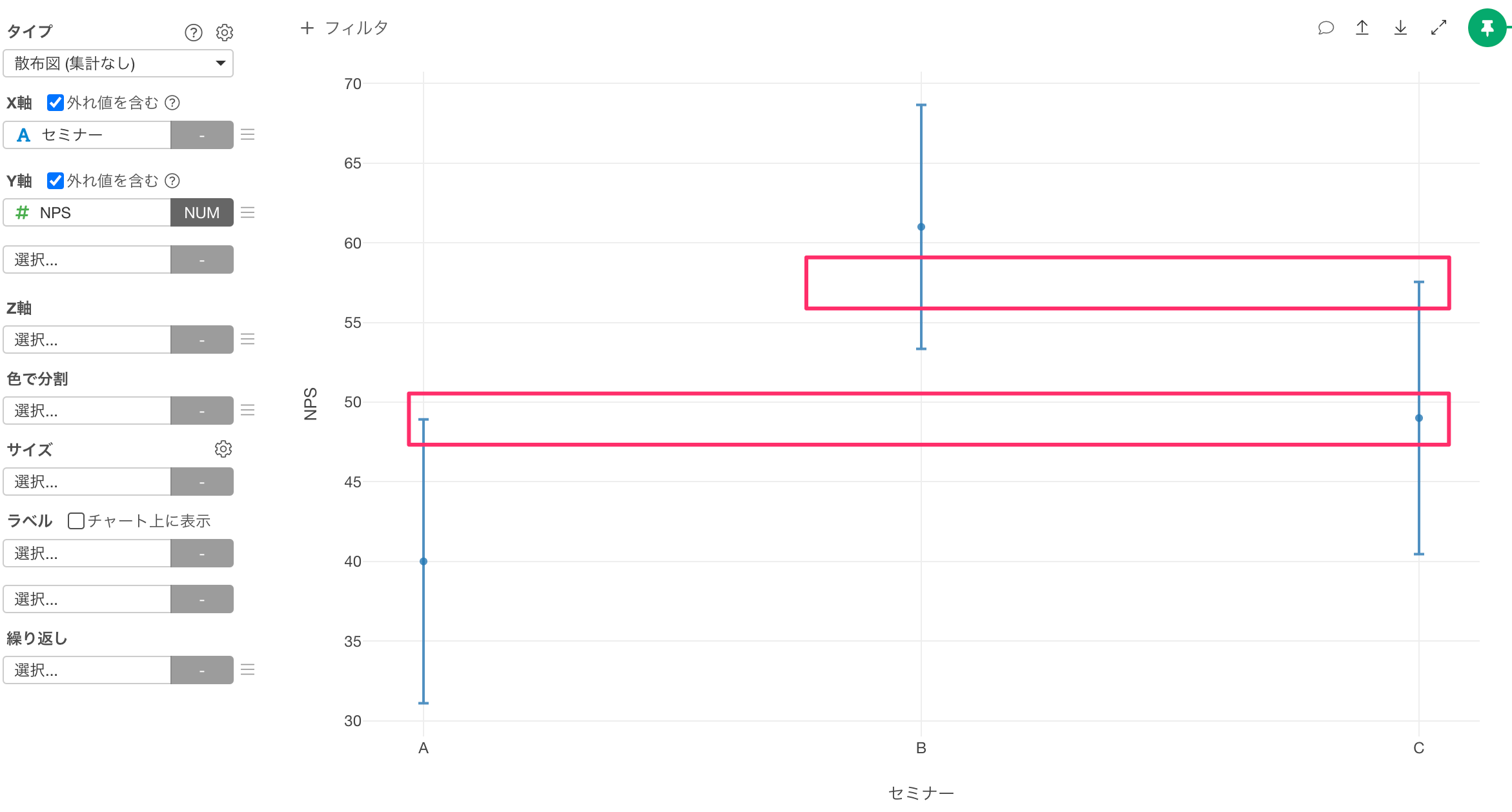
あらかじめ計算しておいた信頼区間を可視化するときにはチャートのタイプに「散布図(集計なし)」を選択します。
今回はセミナーごとにNPSとその信頼区間を可視化したいので、X軸に「セミナー」を選択し、Y軸に「NPS」を選択します。
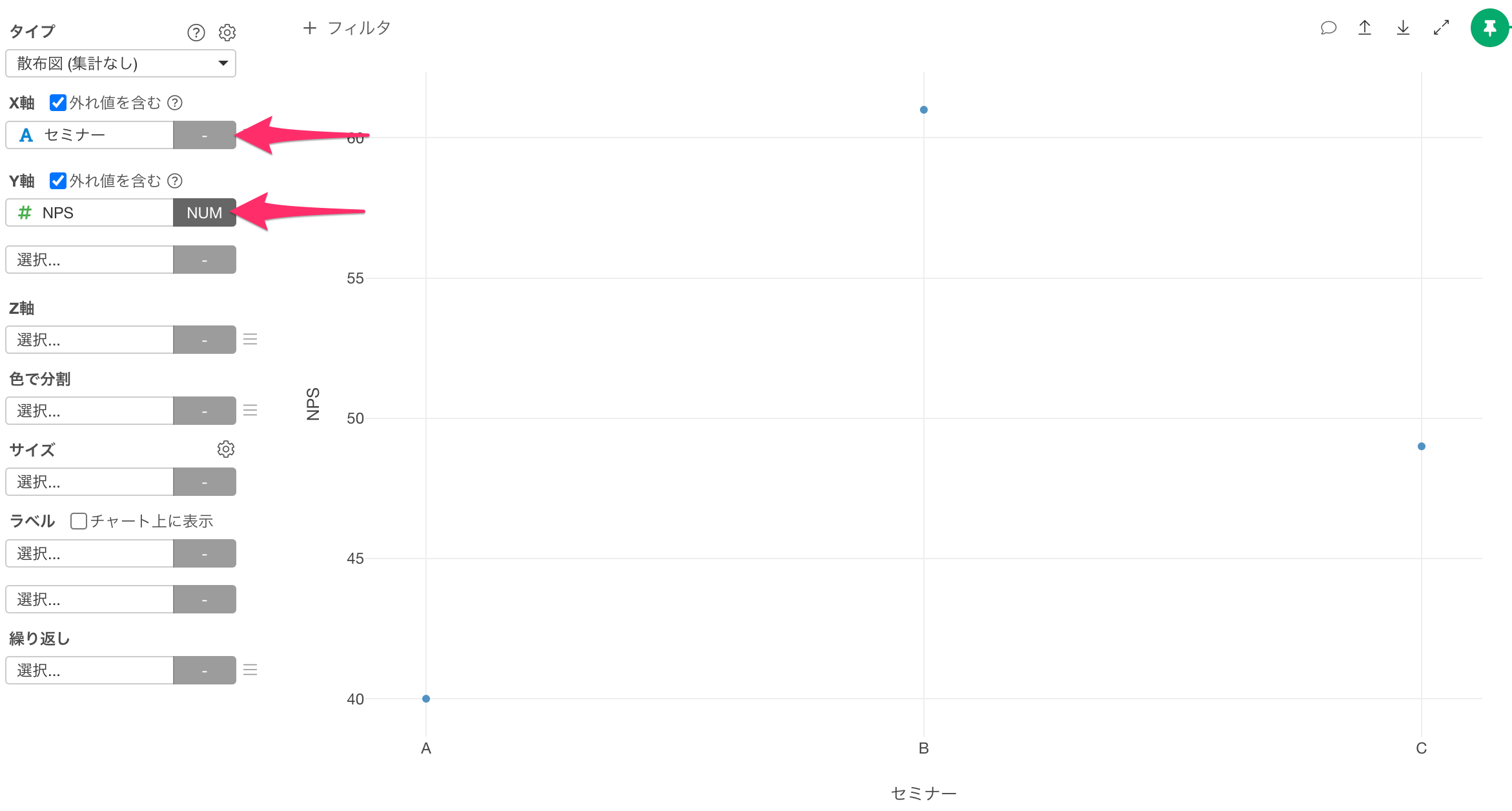
続いて信頼区間を可視化するために、Y軸のメニューから「範囲(信頼区間,etc)」を選択します。
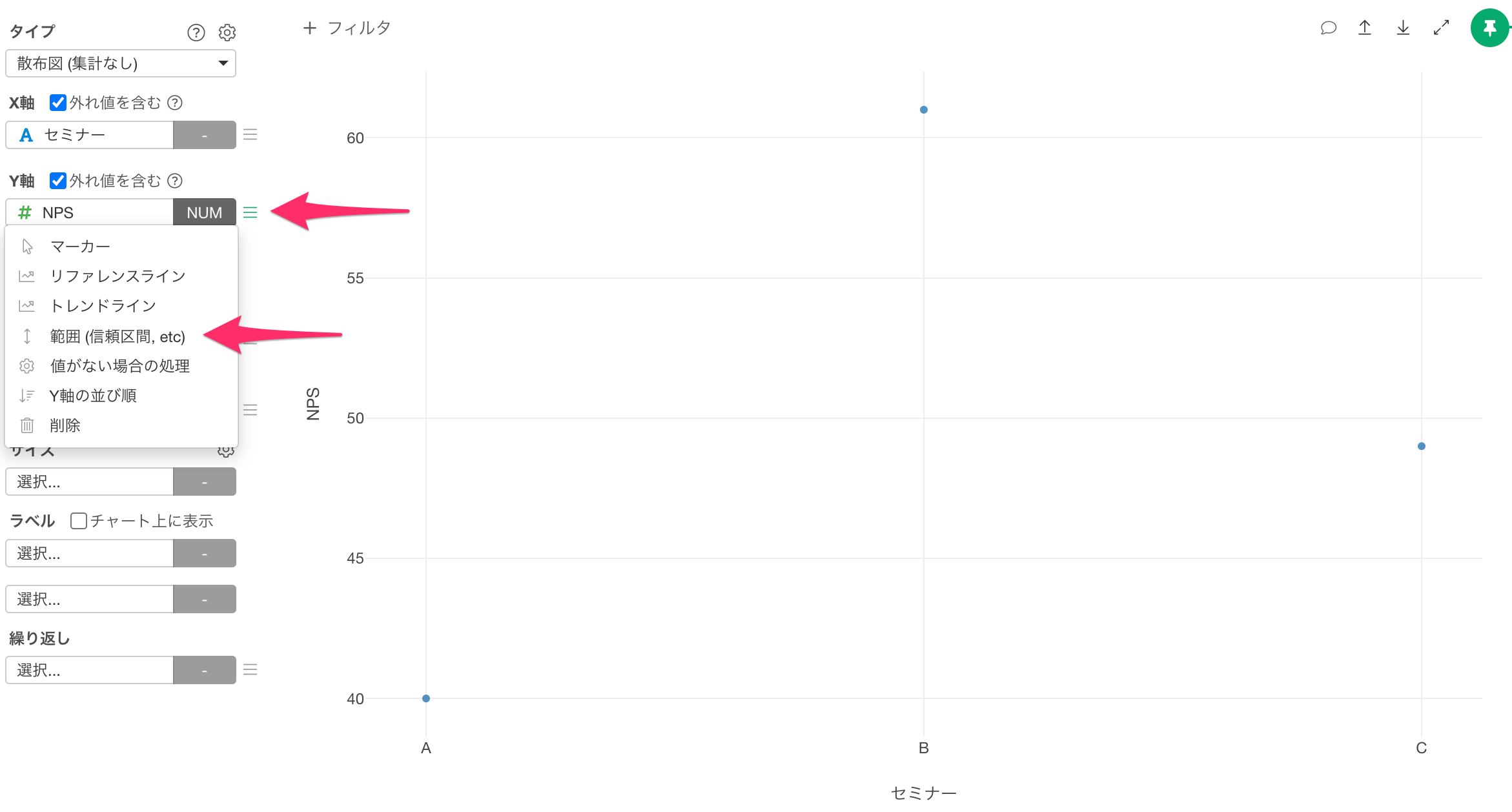
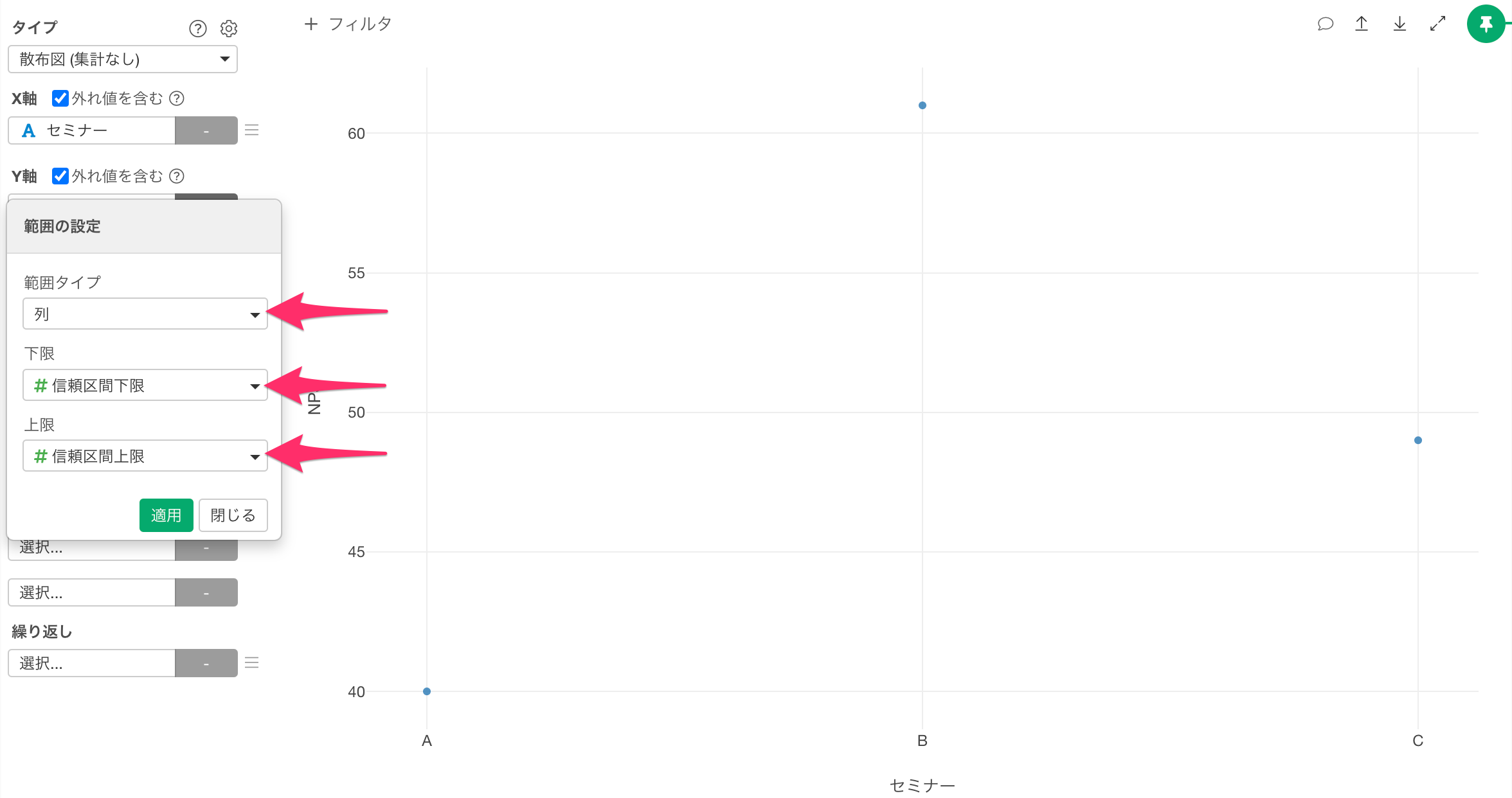
範囲の設定ダイアログが開いたら、範囲タイプに「列」、下限に「信頼区間下限」、上限に「信頼区間上限」を選択し適用します。
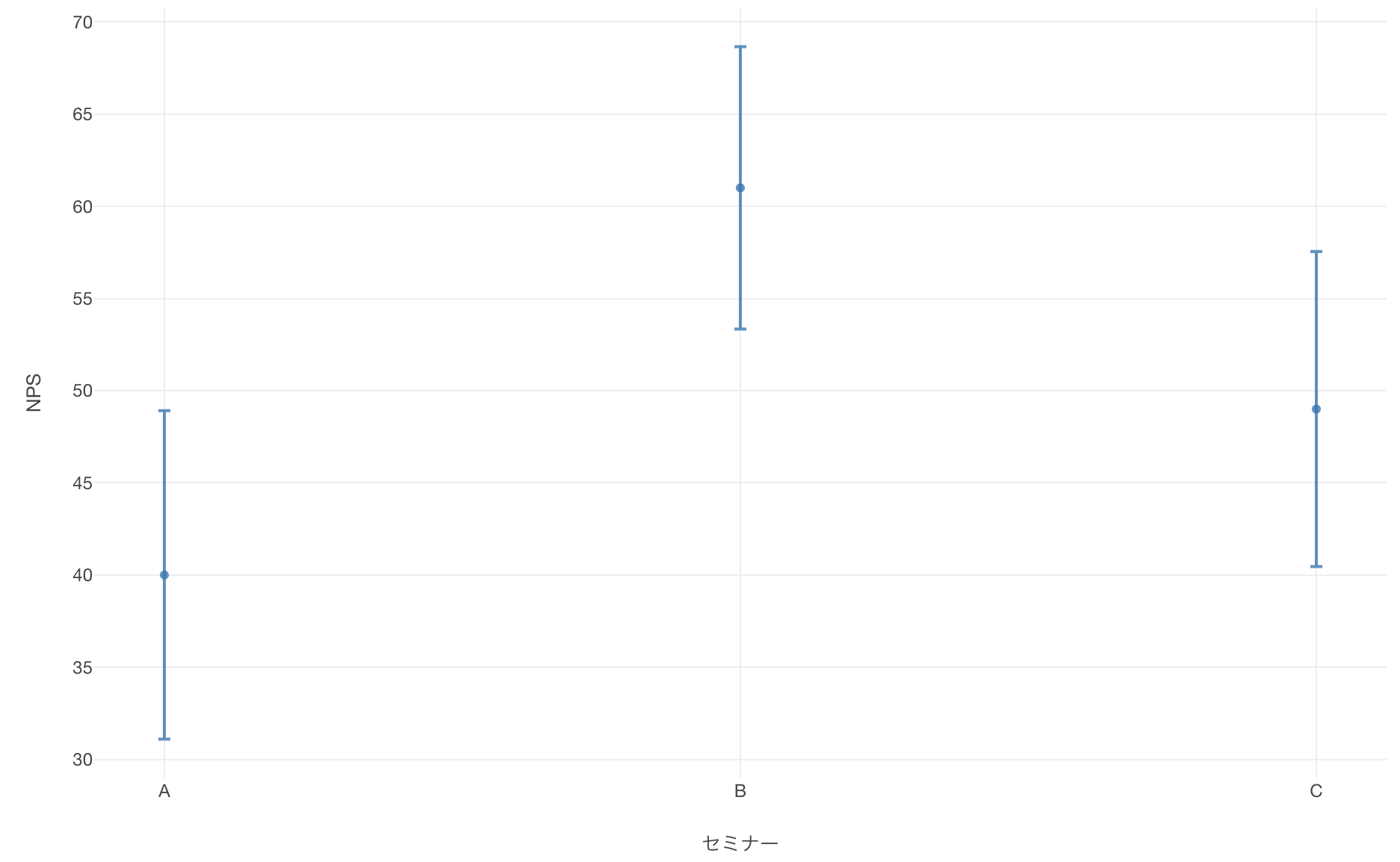
NPSの信頼区間を可視化できました。
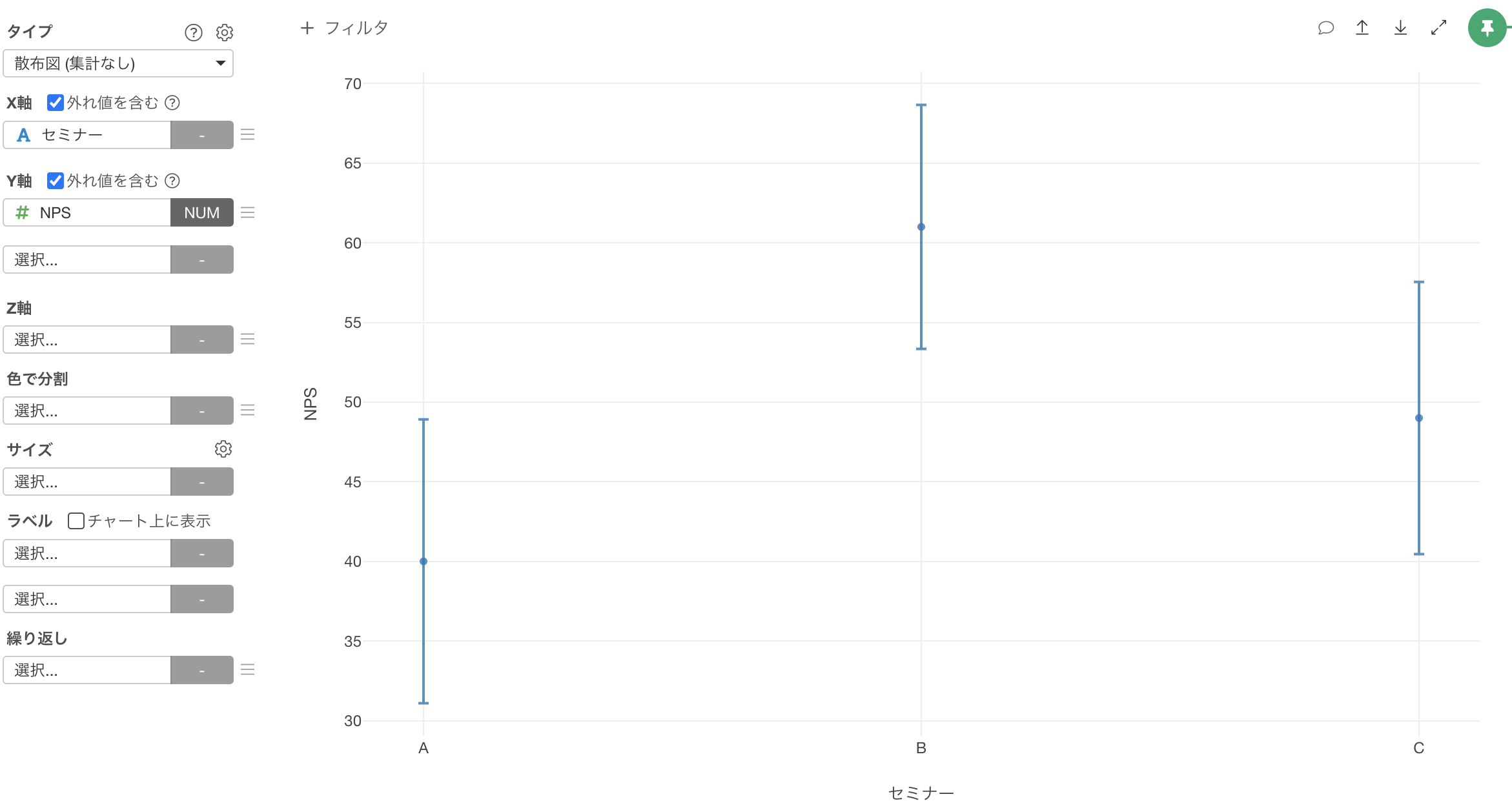
セミナーAとBのNPSの信頼区間は重なっていないため、両者のNPSの間には有意な違いがあると言えそうです。
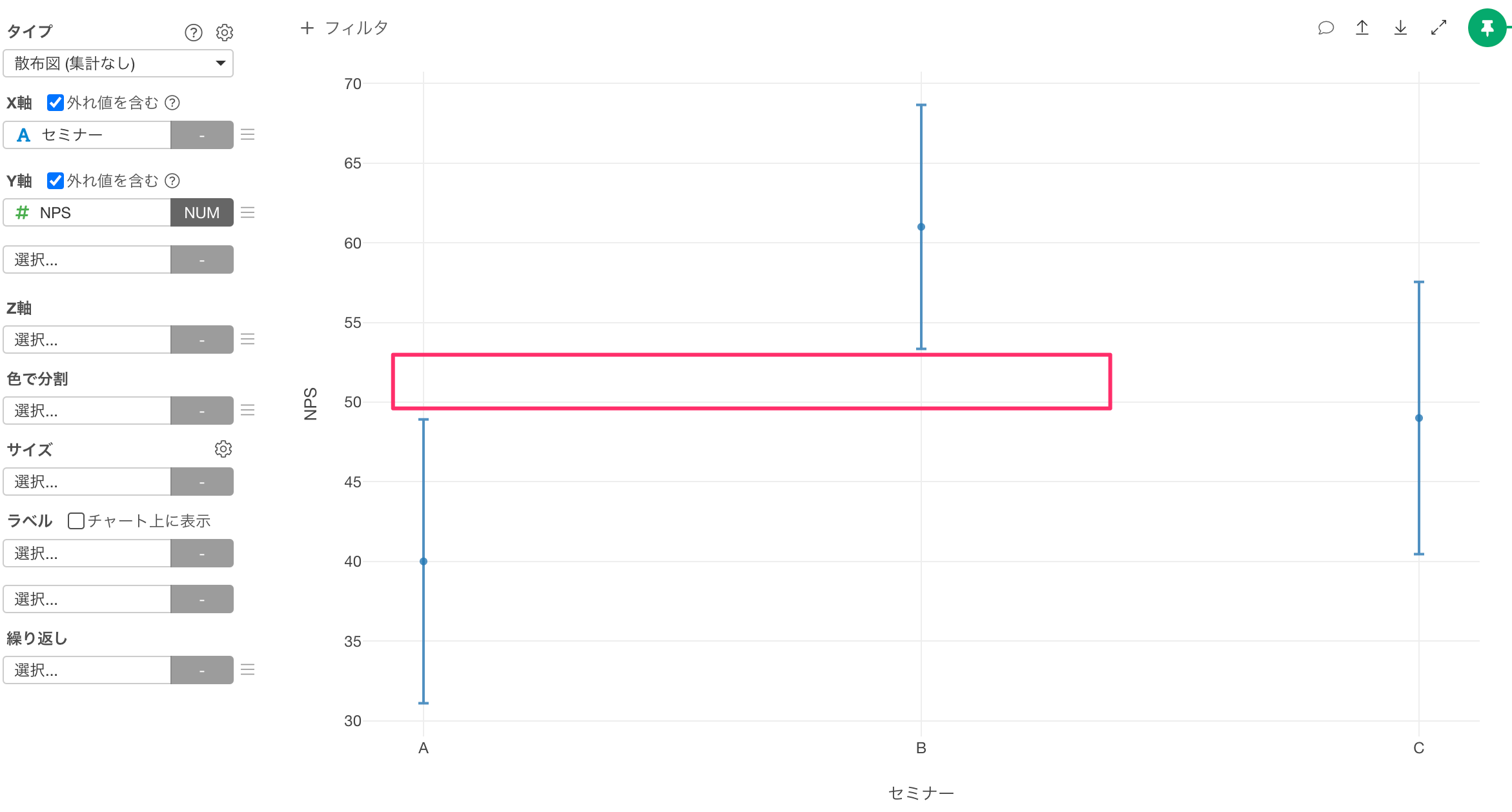
一方で、セミナーAとCあるいは、セミナーBとCのNPSの信頼区間は重なっているので、有意な差があるとは言えないようです。