ロジスティック回帰などの二項分類の統計モデルを実行した際、有意ではないロジカル型または文字列型の変数重要度が最も高いときの解釈方法

多変量解析を行い、例えば、ロジスティック回帰などの二項分類のモデルを実行したときに、ロジカル型や文字列型の説明変数の変数重要度が最も高いにも関わらず、統計的には有意ではなく、それよりも変数重要度が低い他の変数が有意になっている結果に出会うことがあります。

多くの場合、これはデータの構造そのものに起因する現象であり、特に一方向に偏ったパターンでよく見られます。

そこでこのノートでは、よくある一方向に偏ったデータのパターンによって前述したような現象が起きているときの解釈方法を紹介します。

今回は以下のように1行が従業員を表すようなデータを使って、列には各従業員の属性情報を持つデータを使い従業員のデータを使って説明をしていきます。

なお今回は、あらかじめロジスティック回帰のモデルを作成し、前述したような現象が起きているモデルを用意しています。

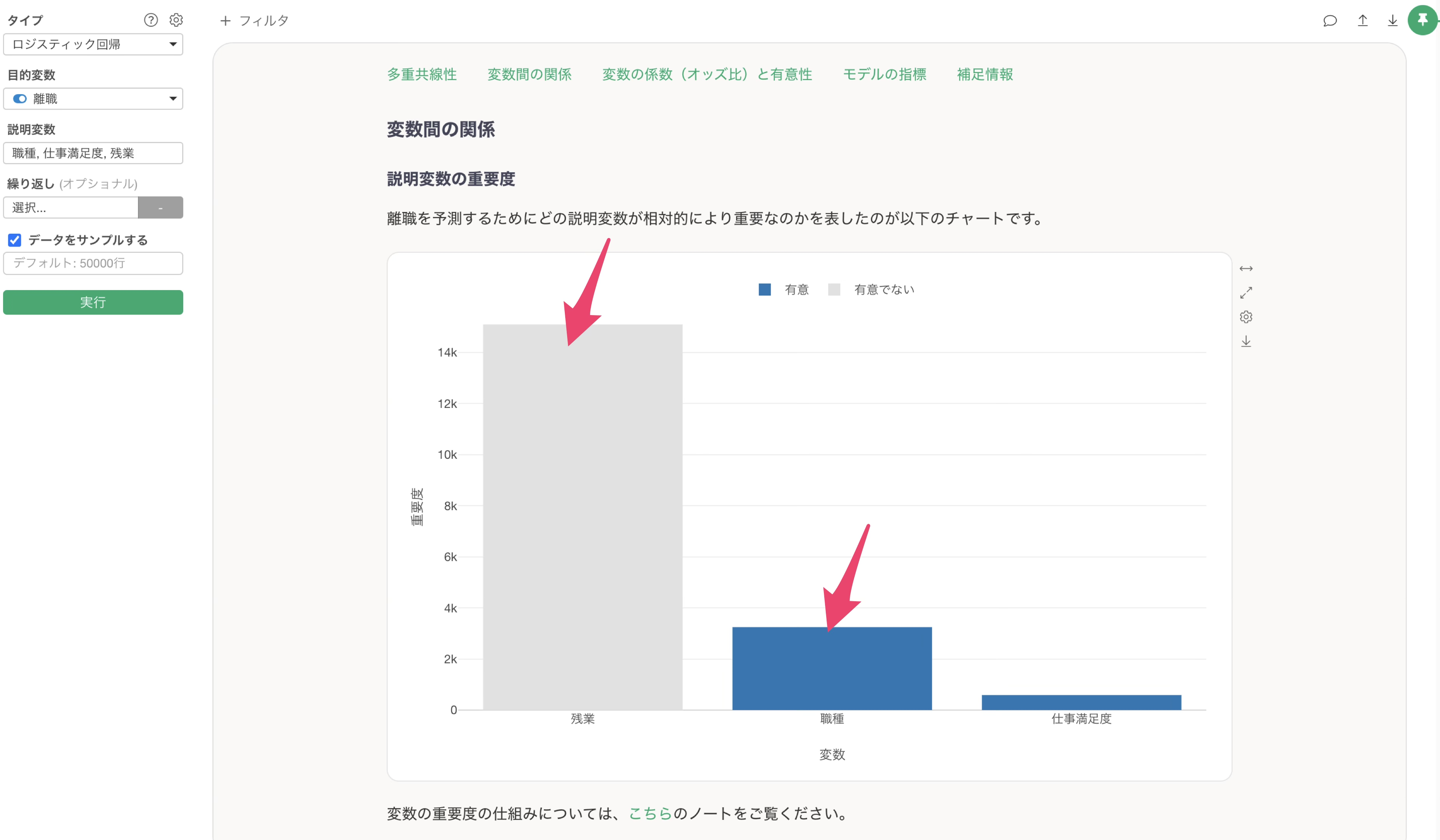
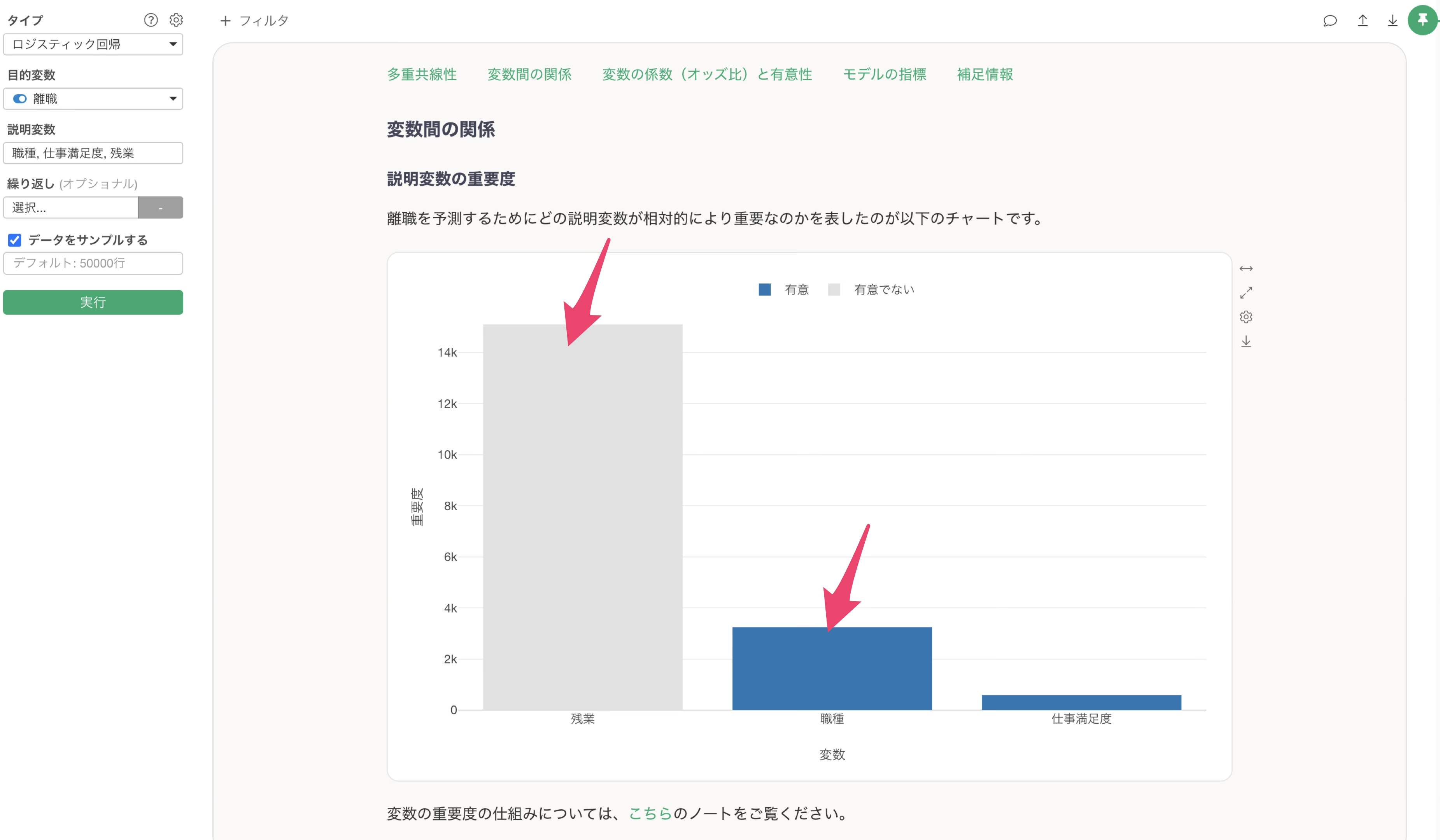
具体的には変数重要度を見ると、最も重要度が高いのは残業であるにもかかわらず、有意とは言えない状況であることに加えて、それよりも変数重要度が低い変数が統計的には有意になっている状態です。

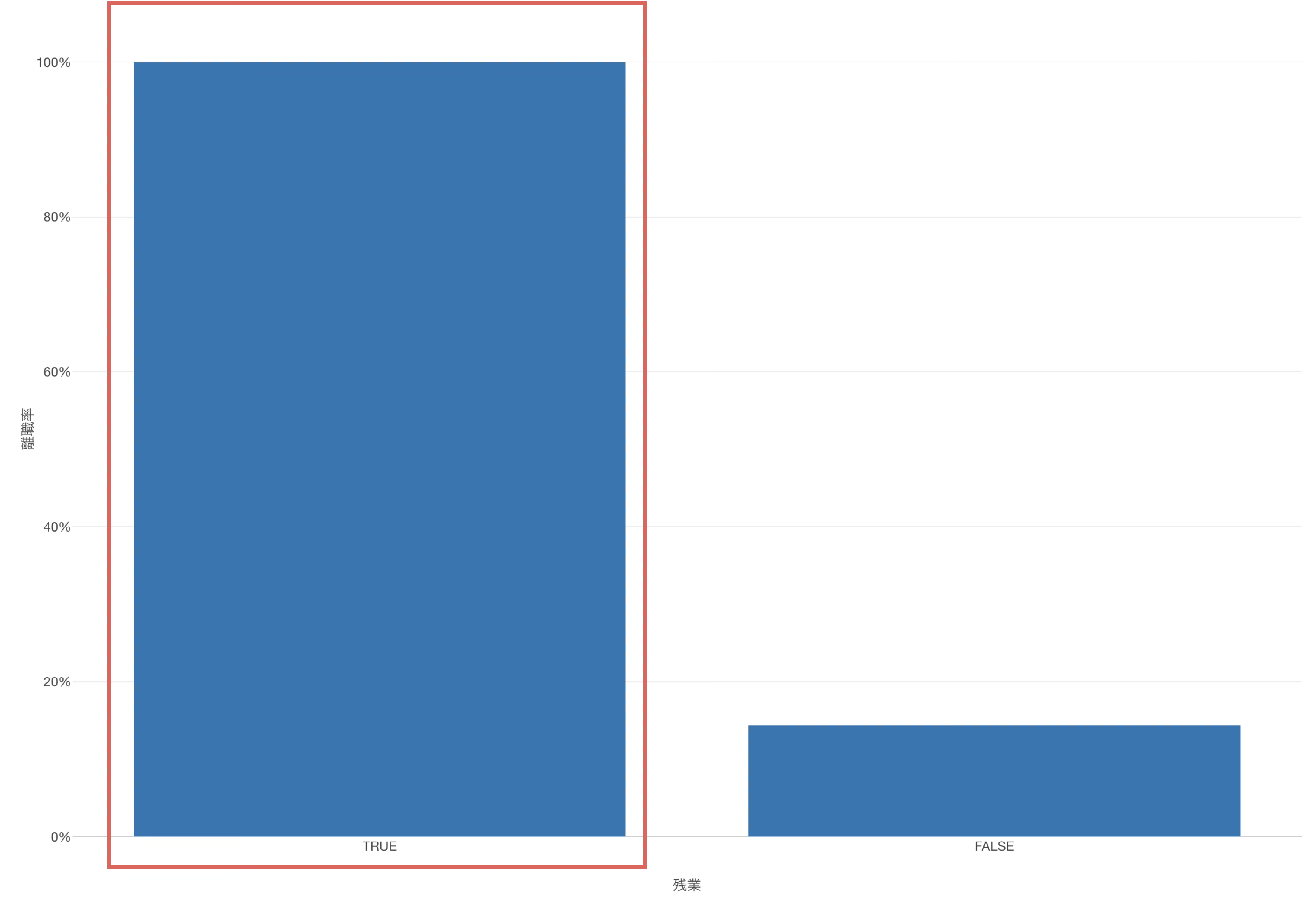
このようなときに、よく起こっていることは、説明変数がTRUEの人（今回の例で言うと残業する人）は、全員が目的変数もTRUE（離職する）である一方で、説明変数がFALSEの人は目的変数がTRUEだったりFALSEだったりする、というような構造です。

なお、逆に、説明変数がTRUEの人（残業する人）は目的変数にTRUEとFALSEが混在していて、説明変数がFALSEの人（残業しない人）は全員、目的変数もFALSE（離職しない）であるような構造もありえます。このように、説明変数の一方の値に対応する目的変数の確率が極端に偏っているような構造があると、今回のような結果が発生します。

これは、説明変数の一方の値（例えば残業がTRUE）で目的変数の値が完全に固定されると、ロジスティック回帰のモデルは「この変数の効果は無限大に大きい」と推定しようとします。しかし、そのような極端な推定値には大きな不確実性が伴うため、統計的な検定では「効果があるとは言い切れない（有意とは言えない）」という結果になります。

今回説明したようなケースが発生しているかどうかは、説明変数の影響度のセクションのチャートから確認が可能です。

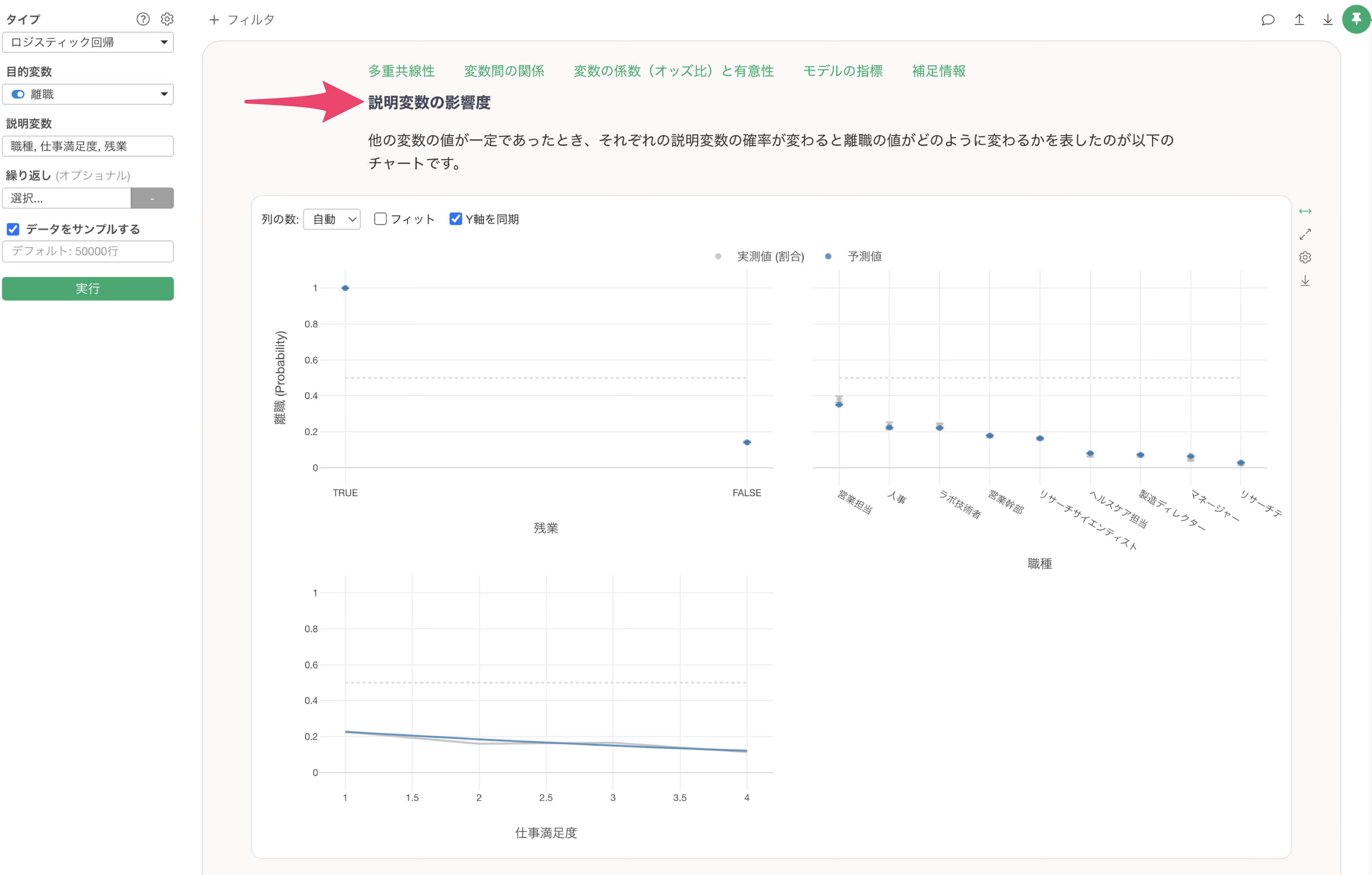
実測値であるグレーの情報、グレーが表す実測値のデータが非常に偏りがある結果であるようであれば、前述したようなケースに該当していると考えられます。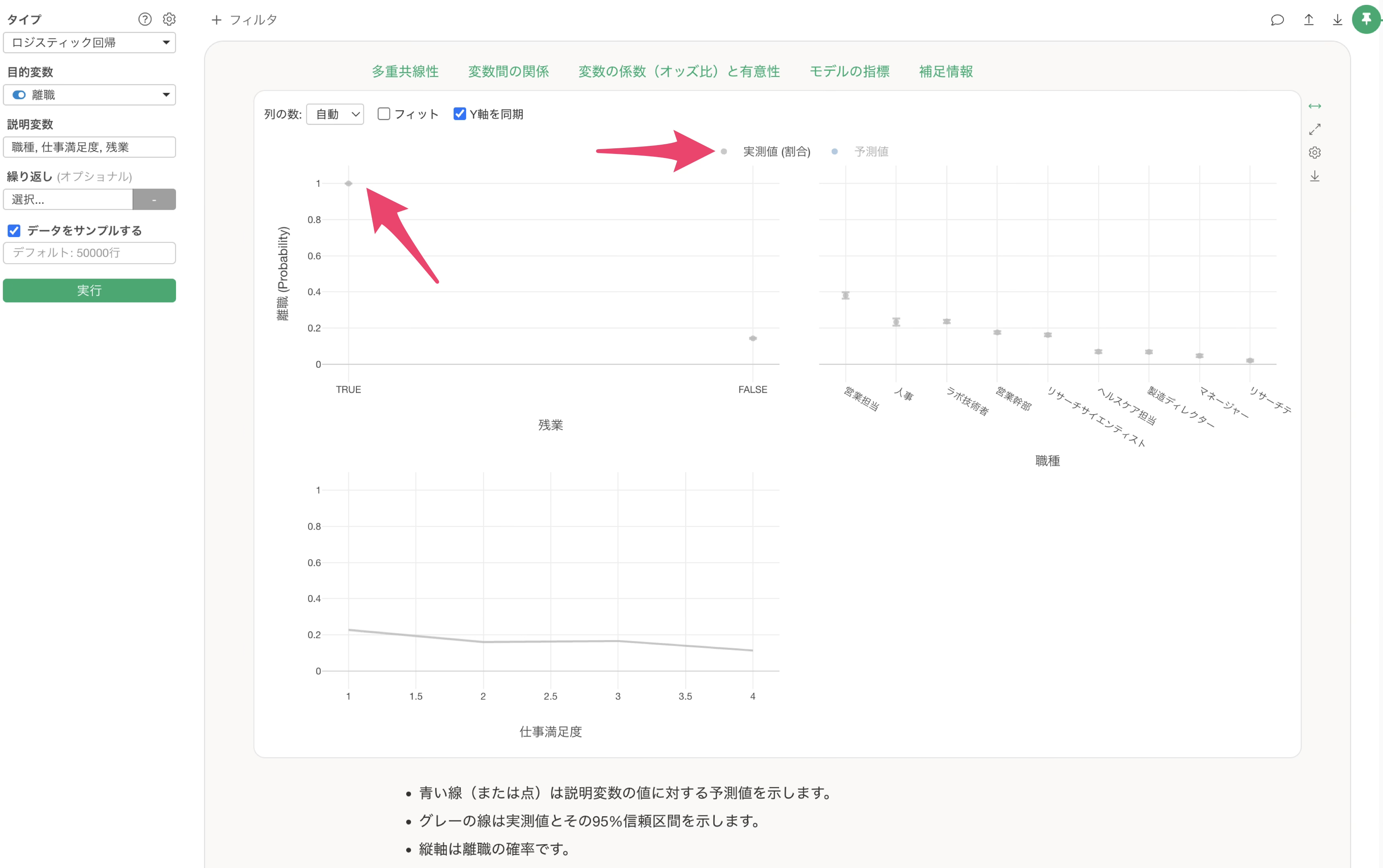

変数重要度が最上位にくる理由

一方で、予測の観点では「その変数の値を見るだけで結果が確実に分かる」ため、変数重要度は最も高くなることがありえます。それは、変数重要度が、その変数がないことでどれだけ精度が悪くなるかをもとに重要度を測る指標だからです。

今回紹介したデータ構造のように、「この変数がTRUEなら結果は100%TRUE」というようなルールが存在すると、モデルの予測精度に絶大な貢献をもたらします。そういった変数を取り除いたり、シャッフルしたりすると、モデルの予測精度は劇的に悪化するため、予測の観点からは最も「重要な」変数として評価されます。

このように、説明変数の統計的な優位性と変数重要度はそれぞれ独立して計算されるため、変数重要度は高いが優位ではないといったような結果が生じます。

なお、変数重要度の計算方法の詳細を確認されたい方は、こちらのリンクをご参照ください。

結果の解釈

なお、このような結果を得られた場合、統計的には有意とは言えないものの、実質的には非常に強い効果を持っている可能性があると考えられます。