R2乗の仕組み
R2乗とは?
R2乗(決定係数)は、作成した予測モデルがどれだけ優秀かを測る指標です。具体的には、目的変数の値の平均からのばらつきをモデルが説明できている割合を表します。
R2乗には以下のような特徴があります:
0から1の間で、1が最高の値
モデルとデータがどれだけフィットしているかを表す指標
相関係数を2乗した値(単回帰の場合)
決定係数、寄与率とも呼ばれる
R2乗の基本的な考え方
R2乗を理解するためには、「平均値からのばらつき」という概念が重要です。
例えば、給料予測のモデルを考えてみましょう。データには平均値の6,500という赤い線があります。
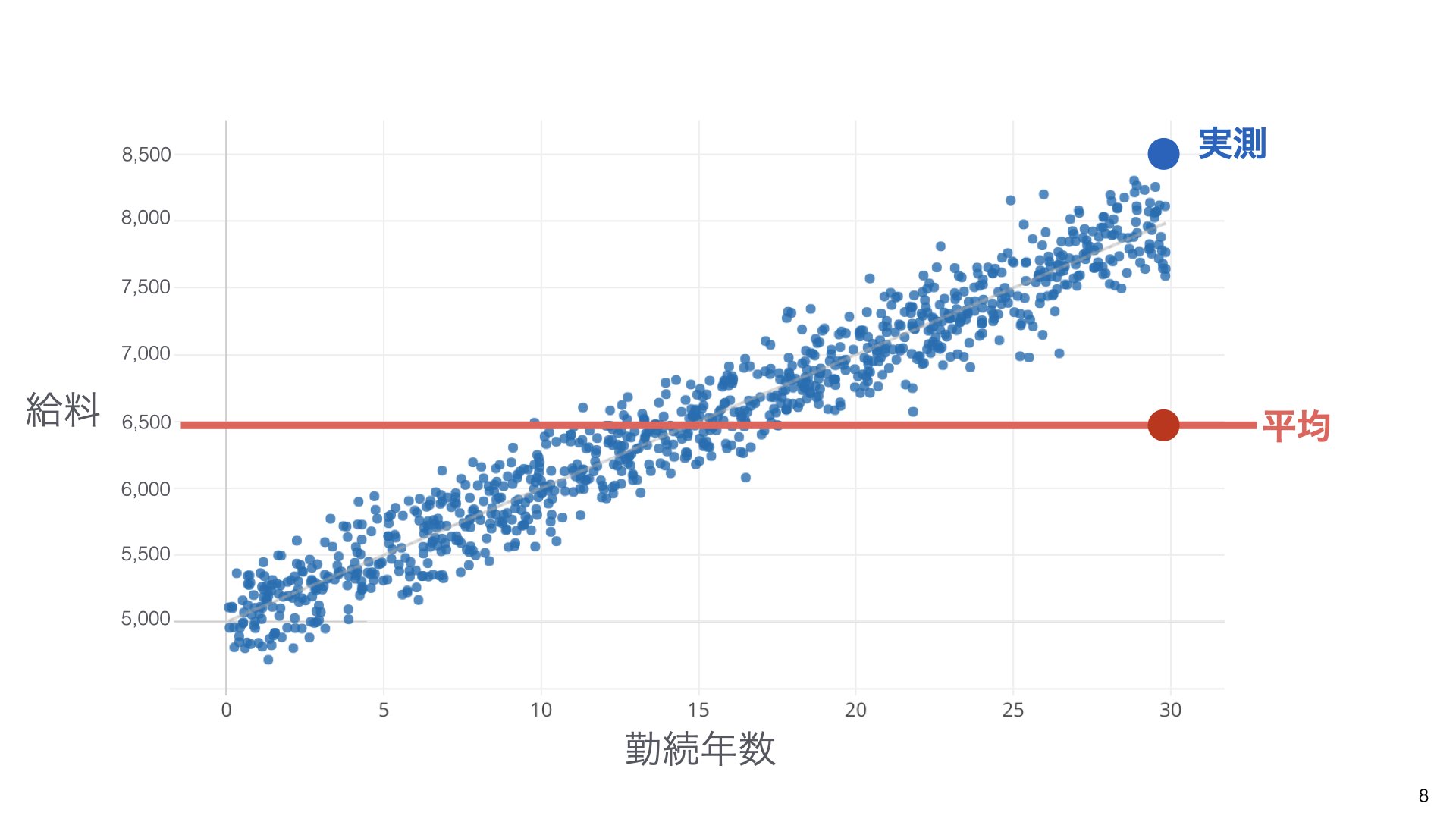
この図では、実際の給料データ(青い点)が平均値の周りに散らばっています。各データポイントは平均値からある程度離れており、この「離れ具合」が「平均値からのばらつき」です。
R2乗が1に近い場合(優秀なモデル)
勤続年数を使って給料を予測する場合を見てみましょう。

このグラフでは、紫色の予測モデル(直線)が実際のデータ点を非常によく説明しています。実際の例では、R2乗が0.944という高い値が得られています。

この高いR2乗値は、勤続年数が給料の94.4%を説明できていることを意味します!
R2乗が0に近い場合(あまり役に立たないモデル)
一方、社内イベントの参加回数で給料を予測しようとした場合を見てみましょう。

この場合、データは平均値の周りにランダムに散らばっており、予測モデル(紫の線)はほとんど平均値と変わらない水平な線になります。これは、社内イベント参加回数が給料とほとんど関係がないことを示しています。
実際のR2乗の計算例
R2乗は以下の数式で計算されます:
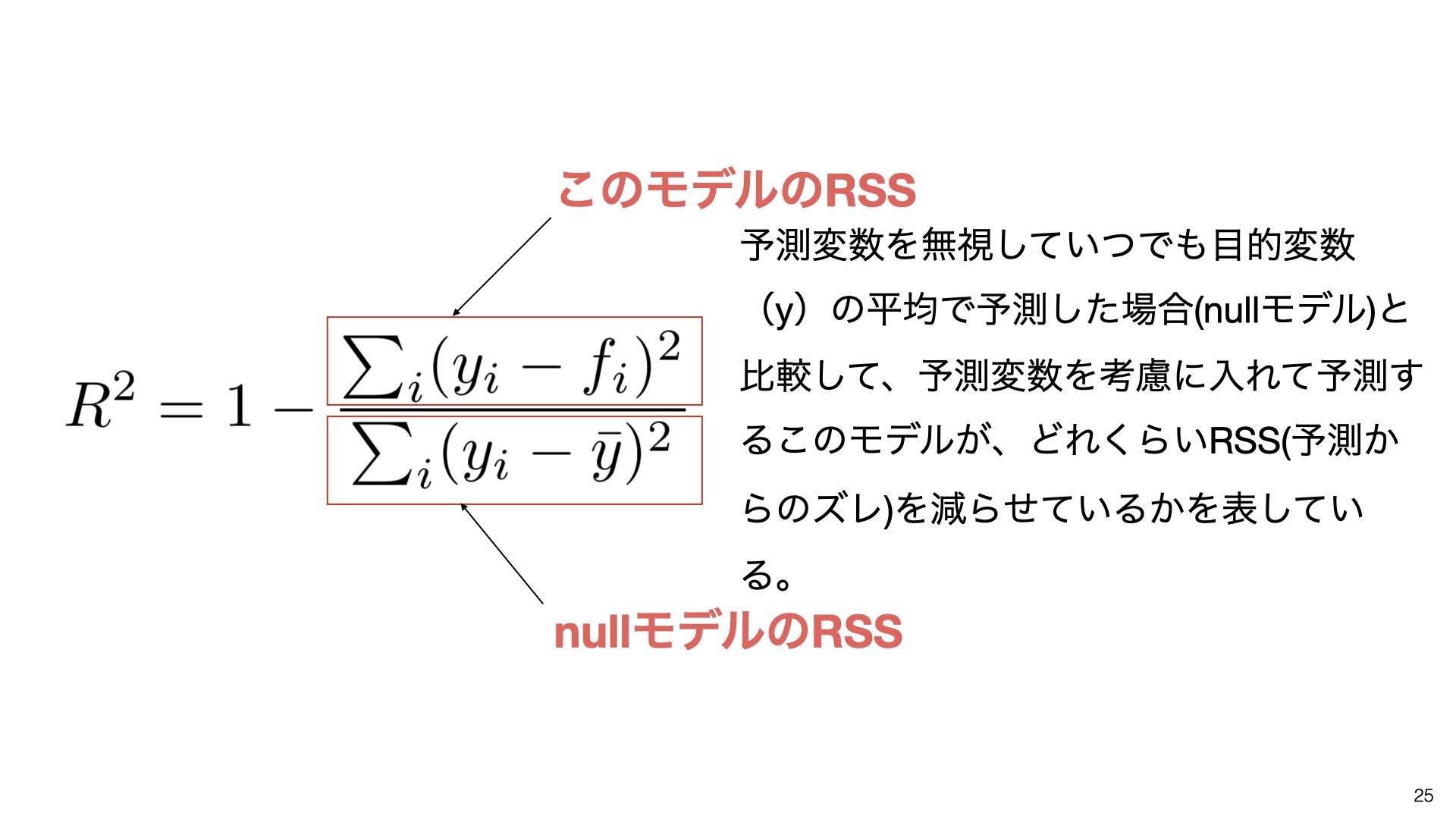
この式を分解すると:
分子:予測モデルによる残差の二乗和(RSS)
分母:平均値を使った場合の残差の二乗和(nullモデルのRSS)
具体的な計算手順

例えば、以下のようなデータがある場合:
- 実際の値(y1)= 10、予測値(f1)= 8
残差 = 10 - 8 = 2
残差の二乗 = 2² = 4
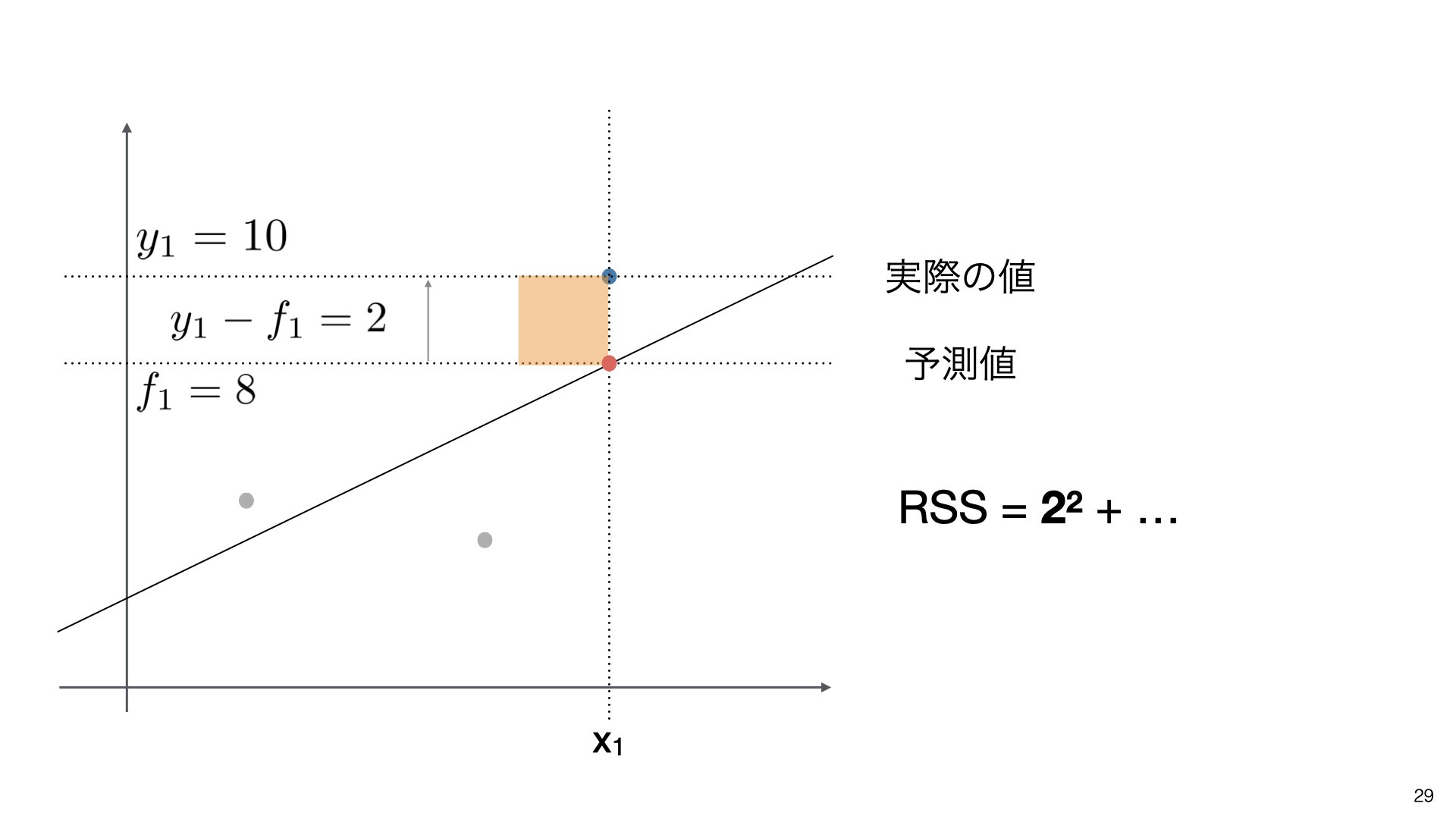
- 全てのデータポイントで同様に計算

- 最終的なRSS = 2² + (-3)² + 1² = 4 + 9 + 1 = 14
この値をnullモデルのRSSと比較することで、R2乗が計算されます。
R2乗の解釈

R2乗が高い:モデルがデータの平均からのばらつきをよく説明している
R2乗が低い:モデルの説明力が限定的で、予測精度が低い
まとめ
R2乗(決定係数)は、回帰モデルがどれくらい上手にデータの「ばらつき」を説明できているかを測る指標で、0から1の間の数値で表されます。これを理解するには「平均値からのばらつき」という考え方が重要です。例えば給料のデータがあるとき、各人の給料は平均給料からある程度離れて散らばっています。
R2乗は、作ったモデル(例:勤続年数から給料を予測)が、この散らばりをどれだけ上手く説明できるかを示します。R2乗が1に近い場合(例:0.944)は、モデルがデータの94.4%を説明できている優秀なモデルで、予測線が実際のデータ点によく合っています。
一方、R2乗が0に近い場合は、モデルがほとんど平均値と変わらない水平線になってしまい、予測に役立たないことを意味します。
R2乗の計算は、モデルの予測誤差と平均値だけを使った場合の誤差を比較することで行われ、「このモデルは平均値を使うよりもどれだけ良い予測ができるか」を数値化したものです。つまりR2乗は、回帰モデルの「成績表」として、データのばらつきをどれだけ説明できているかを教えてくれる指標と言えます。