RMSEの仕組み
RMSEとは?
RMSEとは、Root Mean Square Error(二乗平均平方根誤差)の略で、機械学習や統計学において、予測の精度を測る指標です。簡単に言うと、「実際の値と予測した値がどれくらい違うか」を数値で表したものです。
例えば、給料予測のモデルを作った場合、実際の給料500万円に対して予測値が480万円だったとき、その誤差を評価するために使われます。RMSEの値が小さいほど、予測の精度が高いことを意味します。
RMSEの基本的な考え方
RMSEは、予測モデルの「当たり具合」を測る物差しです。以下のような特徴があります:
大きな誤差により重きを置く:誤差を二乗するため、大きな外れ値があると、その影響が強く反映されます
元の単位と同じ:予測対象が「万円」なら、RMSEも「万円」単位で表示されるため、解釈しやすいです
0に近いほど良い:完璧な予測ができれば、RMSEは0になります
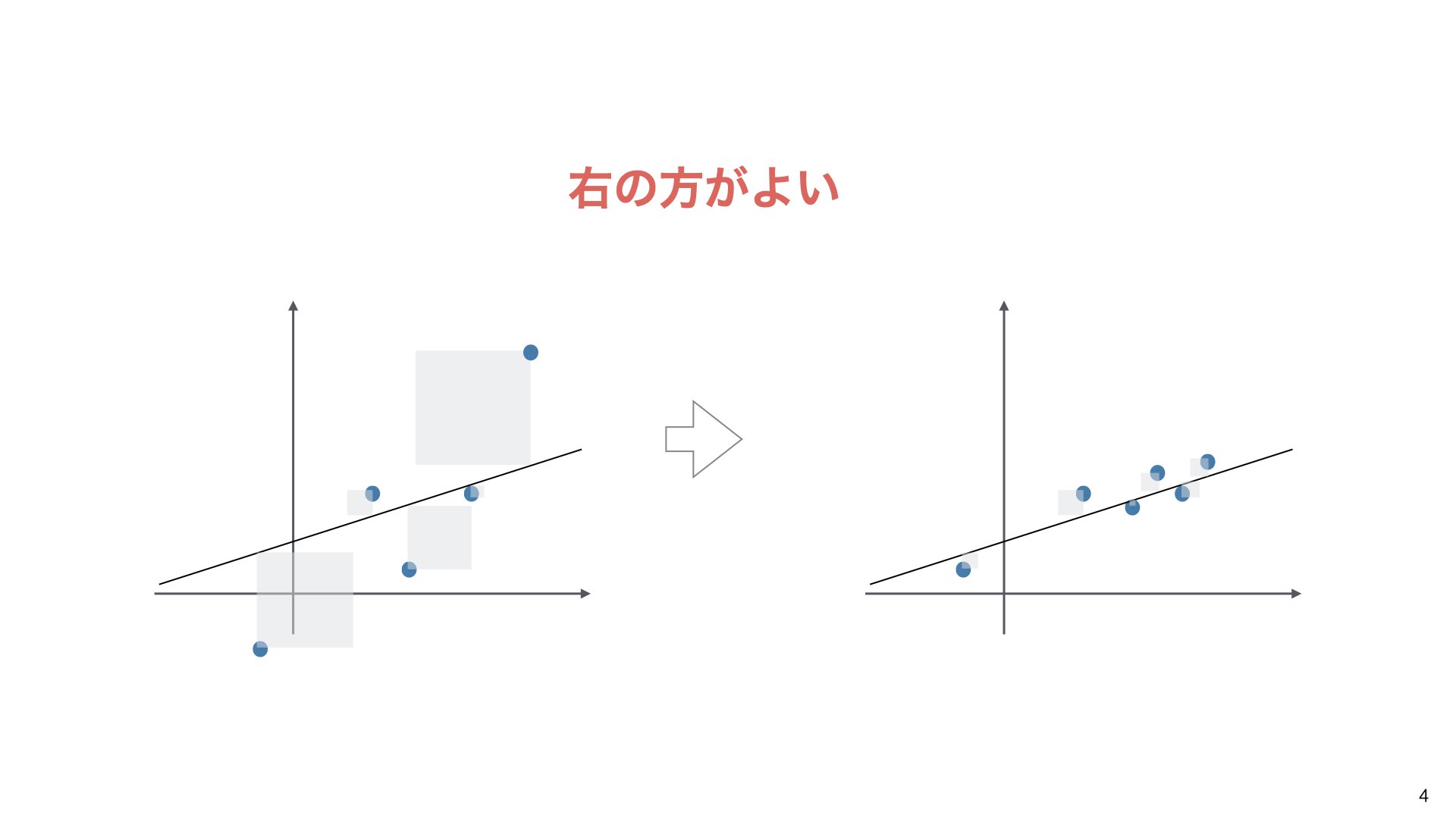
左の図のように予測線から離れた点(外れ値)が多い場合と、右の図のように予測線に近い点が多い場合では、右の方がRMSEの値が小さくなり、「良いモデル」と評価されます。
実際のRMSEの計算例
MAE(平均絶対誤差)との比較
RMSEを理解するために、まずはより単純な指標であるMAE(Mean Absolute Error)を見てみましょう。

MAEは、実際の値(yi)と予測値(fi)の差を絶対値にして、その平均を求めます。図の例では:
データ点1:誤差 = 1
データ点2:誤差 = 2
RMSEの計算手順
RMSEは以下の手順で計算されます:
各データ点について、実際の値と予測値の差を計算する
その差を二乗する(負の値も正の値になる)
すべての二乗誤差の平均を求める
最後に平方根を取る
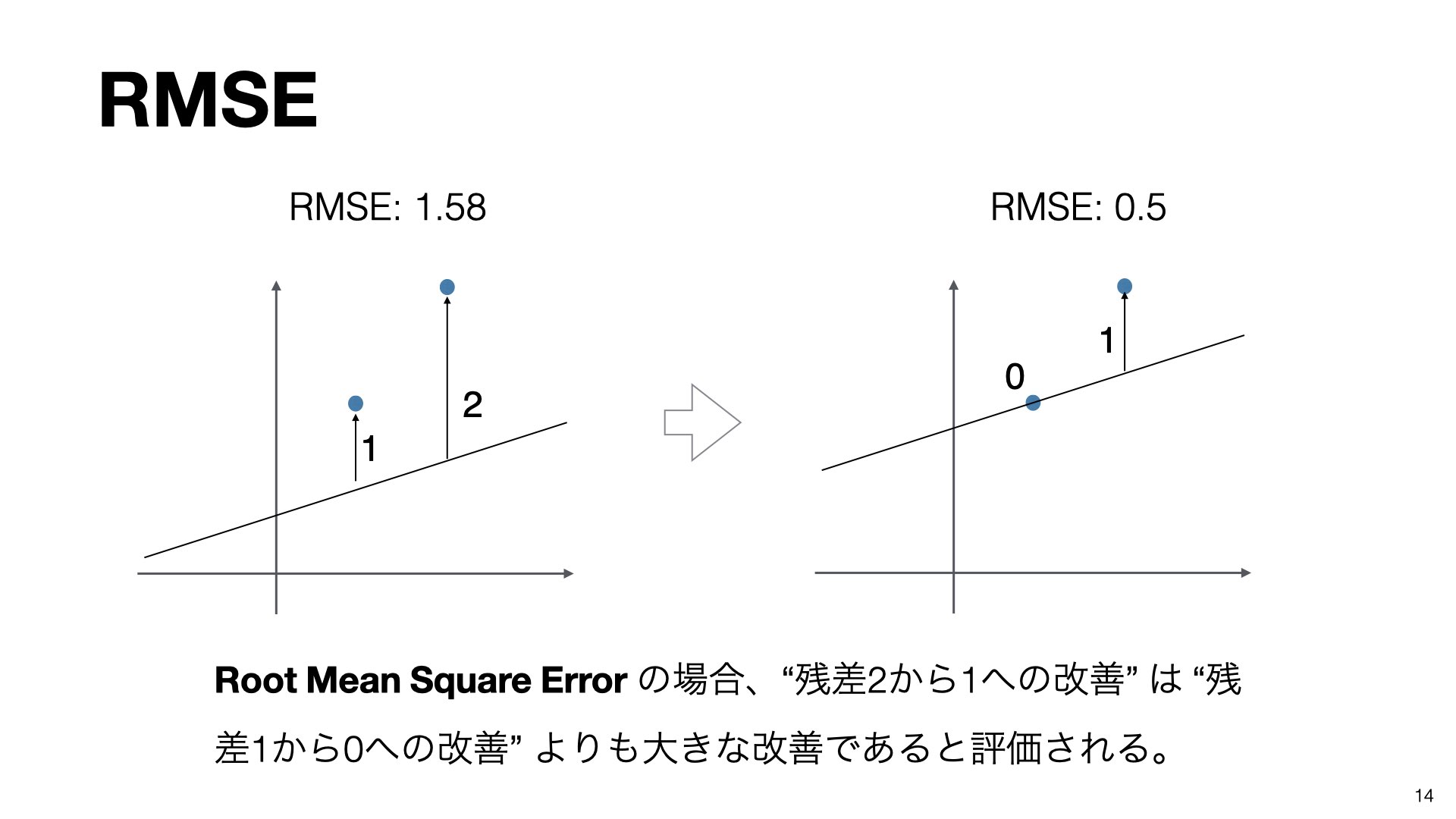
具体的な計算例を見てみましょう:
左の図(精度の低いモデル):
データ点1:誤差1 → 二乗すると 1² = 1
データ点2:誤差2 → 二乗すると 2² = 4
平均:(1 + 4) ÷ 2 = 2.5
平方根:√2.5 = 1.58
右の図(精度の高いモデル):
データ点1:誤差0 → 二乗すると 0² = 0
データ点2:誤差1 → 二乗すると 1² = 1
平均:(0 + 1) ÷ 2 = 0.5
平方根:√0.5 = 0.5
RMSEの重要な特徴
図の下部に記載されているように、RMSEでは「残差2から1への改善」は「残差1から0への改善」よりも大きな改善として評価されます。
これは、RMSEが誤差を二乗することで、大きな誤差により厳しい評価を与えるためです:
誤差2→1の改善:RMSE 1.58→0.5(改善幅:1.08)
誤差1→0の改善:RMSE 0.5→0(改善幅:0.5)
まとめ
RMSEは予測モデルの精度を評価する重要な指標です:
数値が小さいほど良いモデルを意味します
大きな誤差に敏感で、外れ値がある場合にその影響が強く現れます
元の単位と同じなので、実際の業務において解釈しやすいです
モデル同士の比較や、改善の効果を測定する際に広く使われています
給料予測で RMSE = 50万円 なら「平均的に50万円程度の誤差がある」と解釈でき、この値が小さくなるようにモデルを改善していくことが重要です。