予測モデル作成時の説明変数の選び方

機械学習や統計モデルで目的変数（予測したい値）を予測するために、どの説明変数を使うべきかは重要です。

例えば、従業員の給料を予測したい場合、年齢、学歴、職種、勤務年数など様々な要素が考えられますが、すべてを使えば良いというわけではありません。適切な変数を選ぶことで、予測精度の向上とモデルの安定性を両立できます。

説明変数を選ぶ際には、以下の3つの重要な原則があります。

多重共線性を避ける
カテゴリー数の多い変数は避ける
予測をする上で不要な変数（重要でない変数）は除く

これらの原則を守ることで、モデルが安定し、解釈しやすい結果を得ることができます。

1. 多重共線性を避ける

予測モデルの構築において、予測変数間に強い相関関係がある多重共線性の問題は、モデルの係数を不安定にし、分析結果の信頼性を損なう重要な問題の一つです。この問題は線形回帰などの統計のモデルでは発生しますが、ランダムフォレストなどの機械学習のモデルでは起きない問題となります。一方で、機械学習でも似たような問題として影響度を取り合ってしまうことがあるために、機械学習のモデルで予測ではなく要因分析を行う際には注意が必要です。

では、多重共線性が発生するケースをいくつか紹介していきます。

相関の強すぎる説明変数は同時に使わない

相関の強すぎる説明変数を使用してしまうと、多重共線性が発生してしまうことがあります。もし変数間の関係の強さを事前に調べたい場合は、アナリティクスビューから「相関」を行うことで確認が可能です。

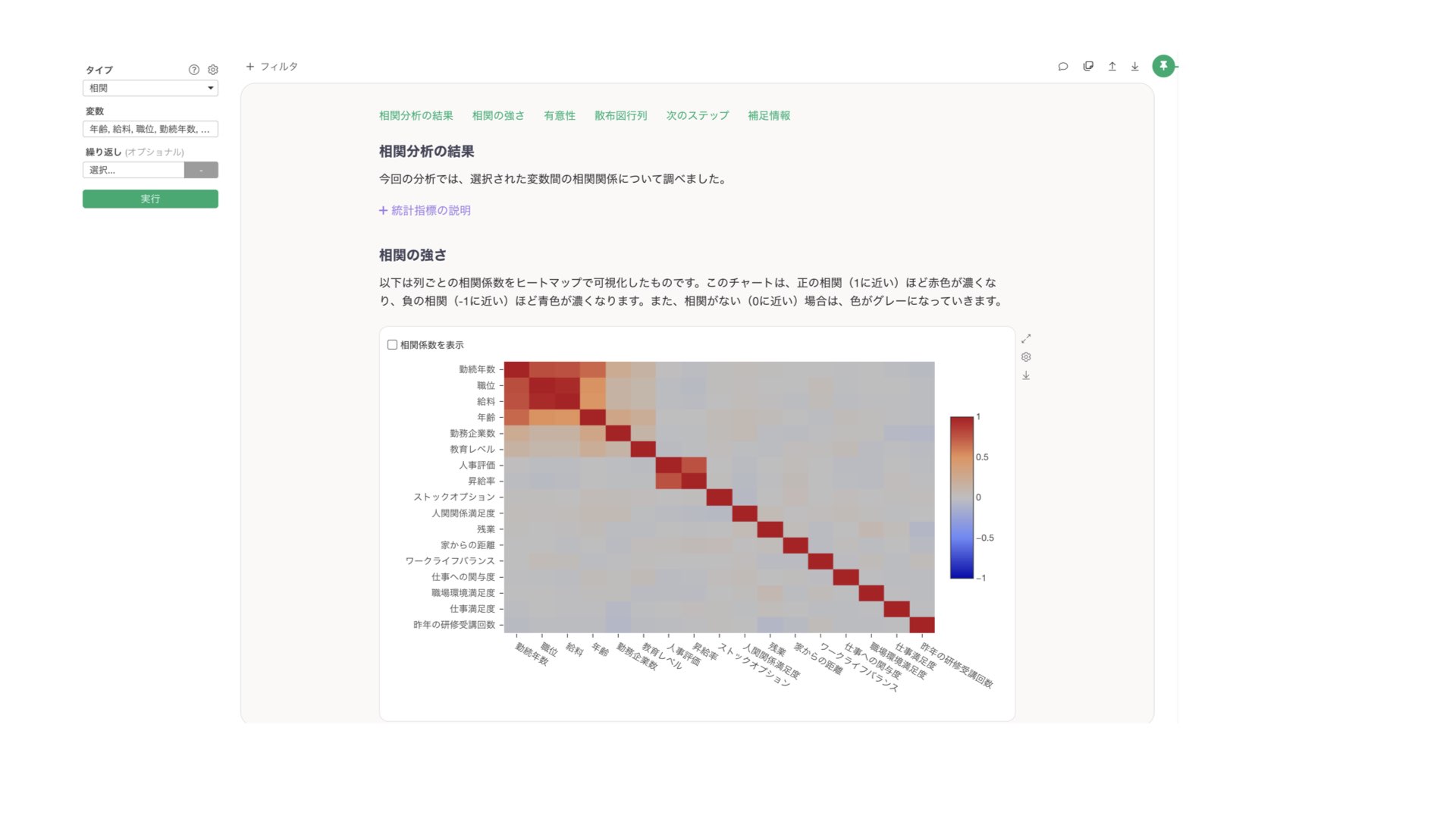例えば、「勤続年数」と「職位」が強い相関を示している場合、これらを同時にモデルに含めると、同じような情報を重複して使用することになり、多重共線性の問題によって係数が不安定になってしまうことがあります。

階層関係のある変数は同時に使わない

階層関係とは、ある変数が別の変数に含まれる関係のことです。

例えば、部署と職種のように階層関係がある変数を使っても、片方の値が分かればもう片方の値もわかってしまうために、多重共線性の問題を引き起こしてしまう原因となります。

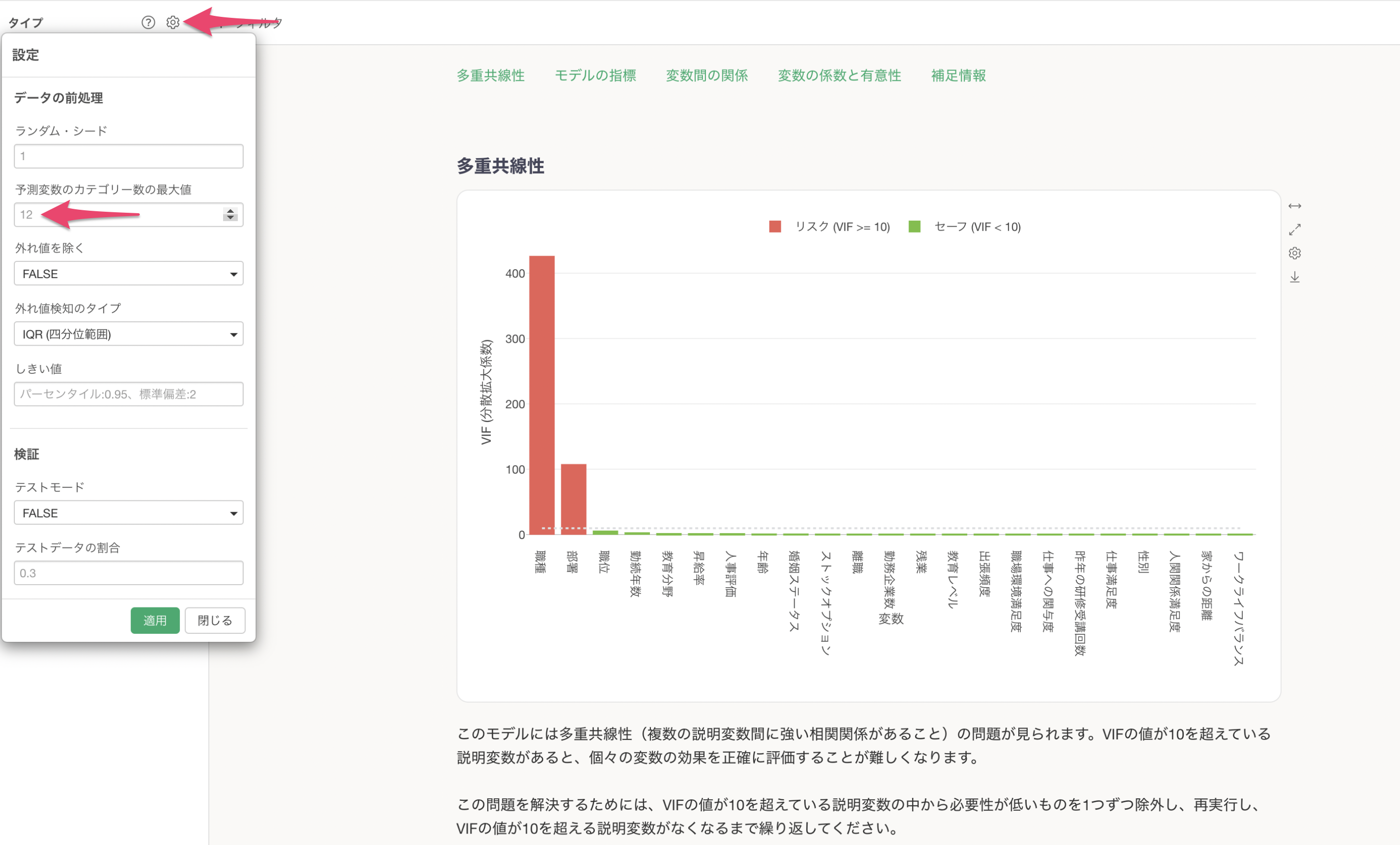
VIFによる多重共線性のチェック

多重共線性を数値的に検出するためにVIF（分散拡大係数）という指標を使用します。

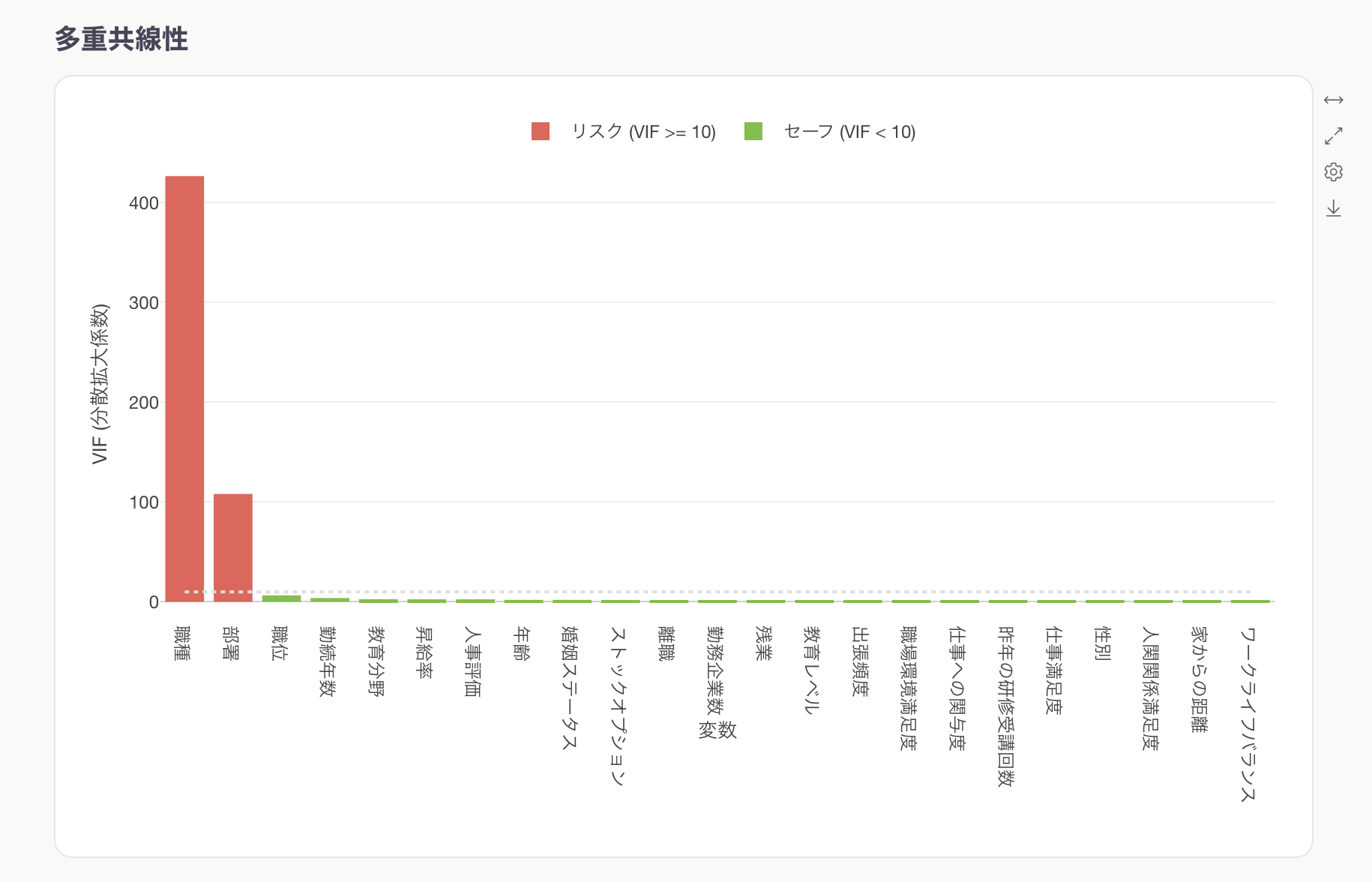
この図では、「職位」と「部署」がVIF値が10以上の変数（赤いバー）が多重共線性の問題を抱えています。

この問題を解決するためには、VIFの値が10を超えている説明変数の中から必要性が低いものを1つずつ除外し、再実行し、VIFの値が10を超える説明変数がなくなるまで繰り返してください。

2. カテゴリー数の多い変数を避ける

カテゴリー変数（文字や分類データ）で、あまりに多くの種類がある場合は注意が必要です。

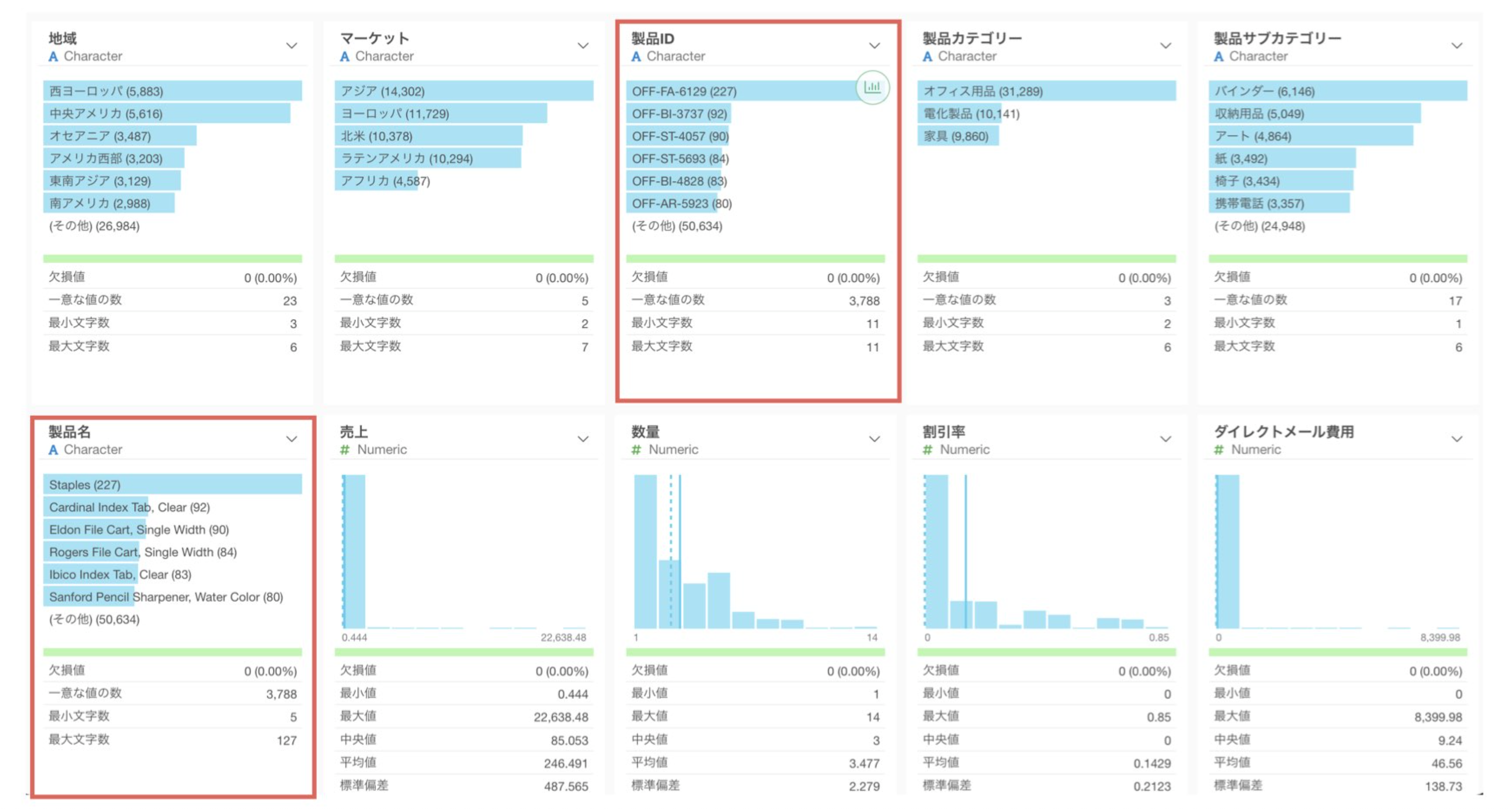
上の例では、「製品名」や「製品ID」に3,788種類もの値があります。このような変数を使用しても、全ての値をそのまま組み込むことは難しいために、その変数を使っても意味がない結果になってしまうことがあります。また、もし全ての値を使って予測を使用としてもモデルが複雑になってしまい、予測精度が悪化してしまう可能性もあります。

Exploratoryの場合は、説明変数のカテゴリーの数の最大値のデフォルトは「12」となっているため、カテゴリー数を変更しない限りは12個だけが使われます。

一意な値の数が多すぎる場合は、詳細なカテゴリーの値を持った列を使うのではなく、「上位のカテゴリー」の列（例: 製品カテゴリー）を使用した方が望ましいです。

モデル実行後の変数選択最適化

基本的な変数選択を行った後、予測モデルを実行してから、さらに変数選択を最適化することができます。

変数の重要度と統計的有意性を元に評価する

変数重要度を元に、各説明変数がモデルの予測性能にどの程度重要かを確認できます。さらには、このチャートでは統計的に有意か、有意でないかの情報も確認できます。

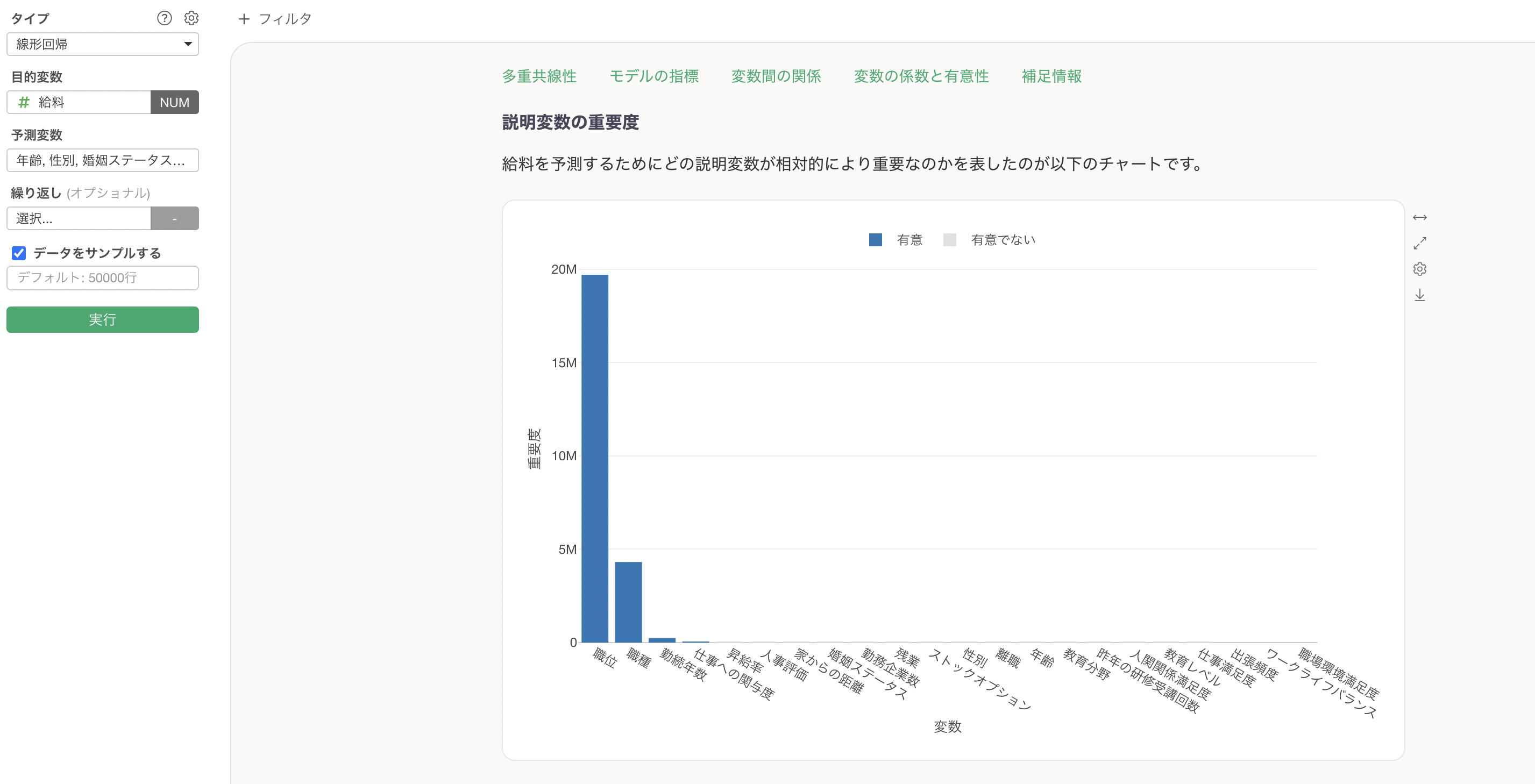
この変数重要度で見た際に、重要度の低い変数を除去していく、さらに統計的に有意でない変数を取り除いていくことでモデルをシンプルにしてしていくことができ、過剰適合のリスクも減らすことができます。

しかし、統計的に有意でなくても、影響度のチャートを見て目的変数との関係がありそうなものを除いてしまうことで、予測精度が落ちてしまうことがあるために注意が必要です。

まとめ

機械学習や統計モデルで目的変数を予測する際、適切な説明変数選択が予測精度とモデル安定性の鍵となります。選択時の重要な原則として、まず多重共線性を避けることが挙げられます。

相関の強い変数や階層関係のある変数の同時使用は係数を不安定にするため、VIF値を用いて10以下に抑える必要があります。次に、カテゴリー数の多い変数は避け、より上位のカテゴリーを使用します。

最後に、モデル実行後は変数重要度と統計的有意性を確認し、重要度の低い変数や有意でない変数を除去してモデルを最適化します。

これらの原則に従うことで、過剰適合を防ぎ、解釈しやすく安定した予測モデルを構築できます。