時系列データにおける異常値検知の方法
異常値検知は、データ内で通常のパターンから著しく逸脱したデータ(異常値、外れ値)を特定することです。この異常値検知は、製造工程における品質管理やシステムの異常検知、不正取引の発見など、様々な分野で重要な役割を果たしています。
異常値を早期に発見することで、問題への迅速な対応が可能となり、品質の向上とコストの削減を実現できます。
また、リスク管理の観点からも、異常値検知は事業の安定的な運営において不可欠な要素となっています。
標準偏差を使った異常値検知
一般的に知られる異常値検知は、平均値から標準偏差の2倍や3倍の範囲を超えたものを異常値として設定します。
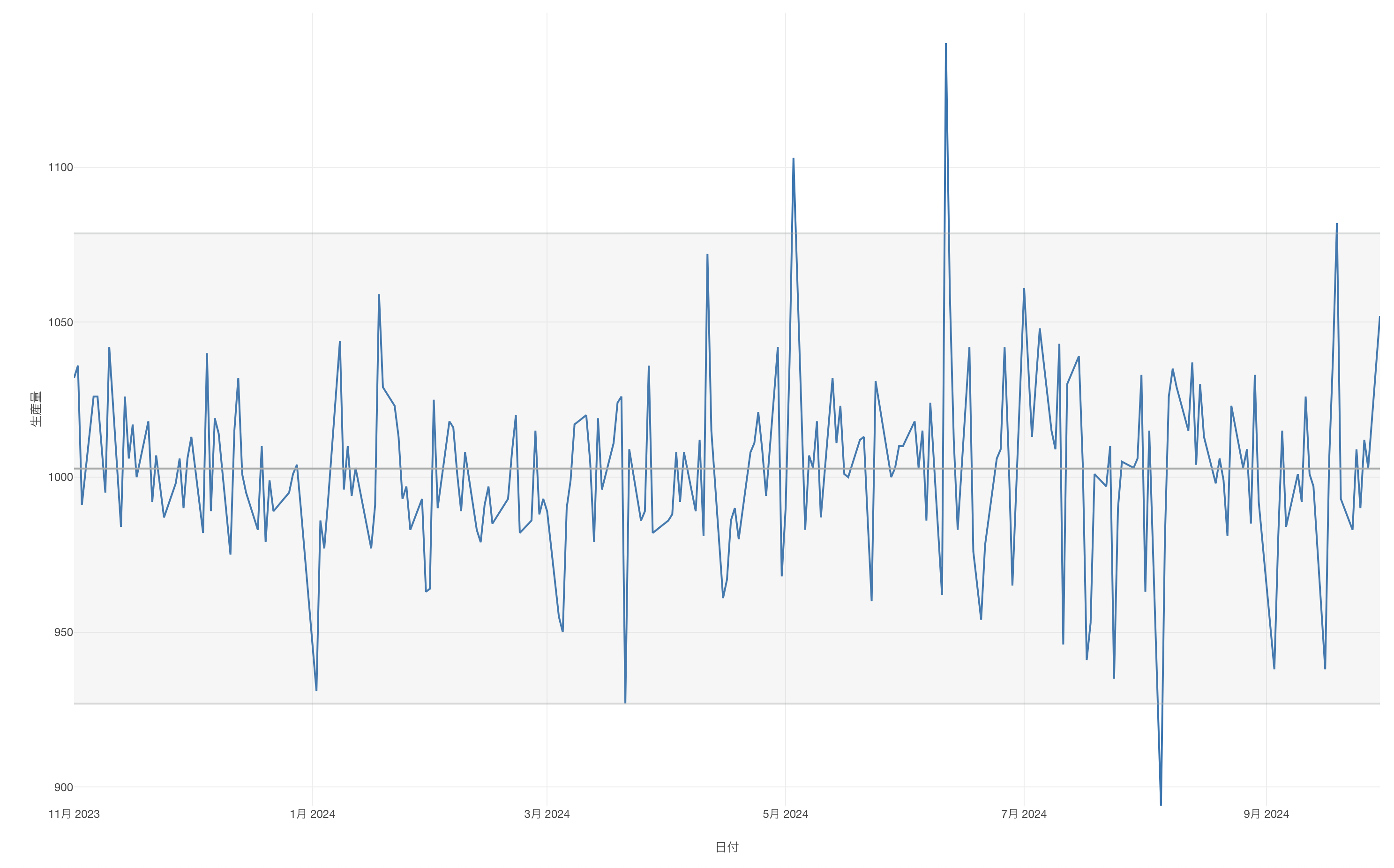
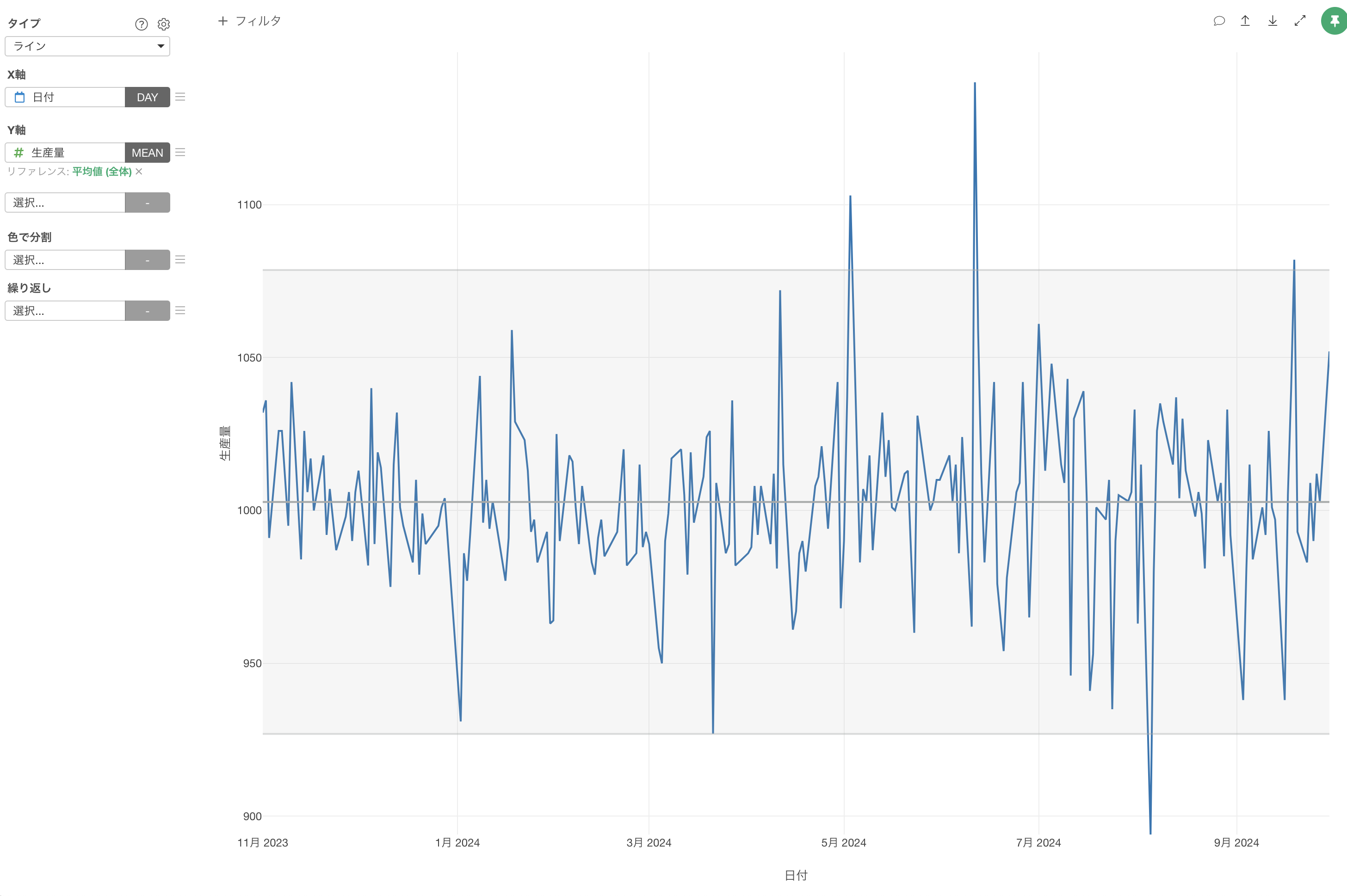
例えば、以下のように日毎の生産量のデータがあったとします。
ラインチャートにて、X軸に「日付」、Y軸に「生産量」を割り当てて可視化をしていたとします。
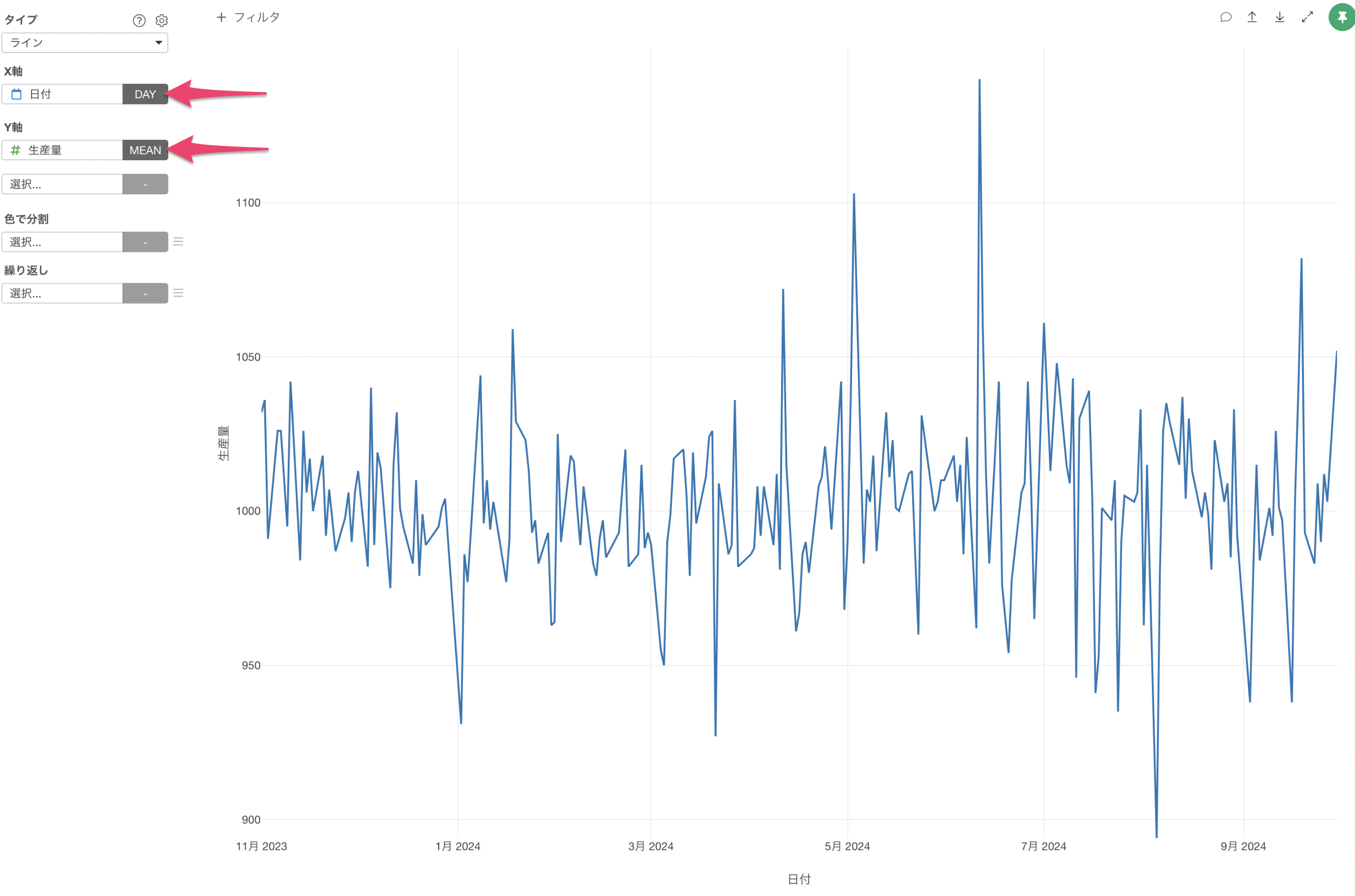
このデータをもとに異常値検知を行っていきます。
Y軸のメニューから「リファレンスライン」を選択します。
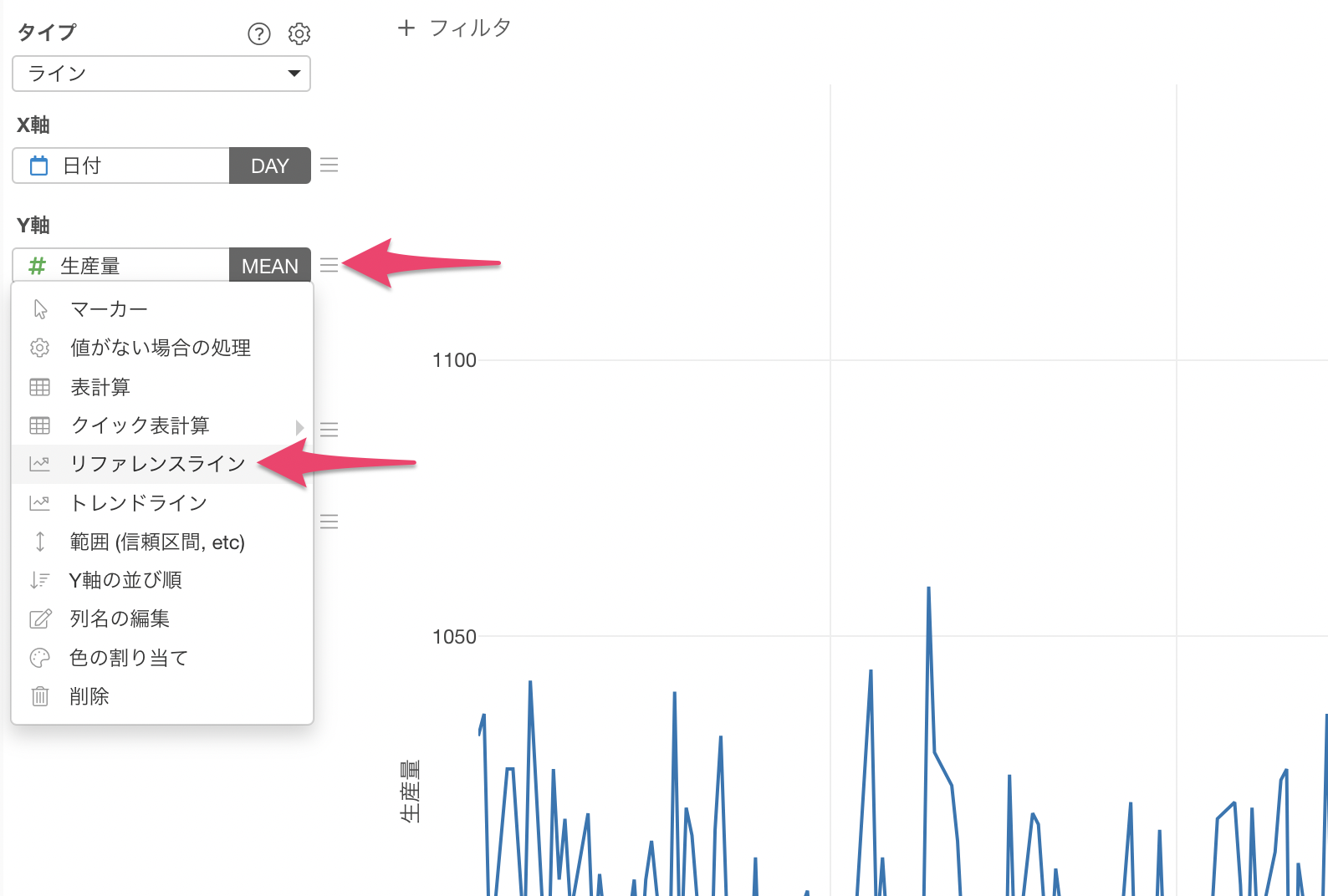
リファレンスラインの設定のダイアログが表示されるため、リファレンスラインのタイプには「平均値(MEAN)」を選択します。
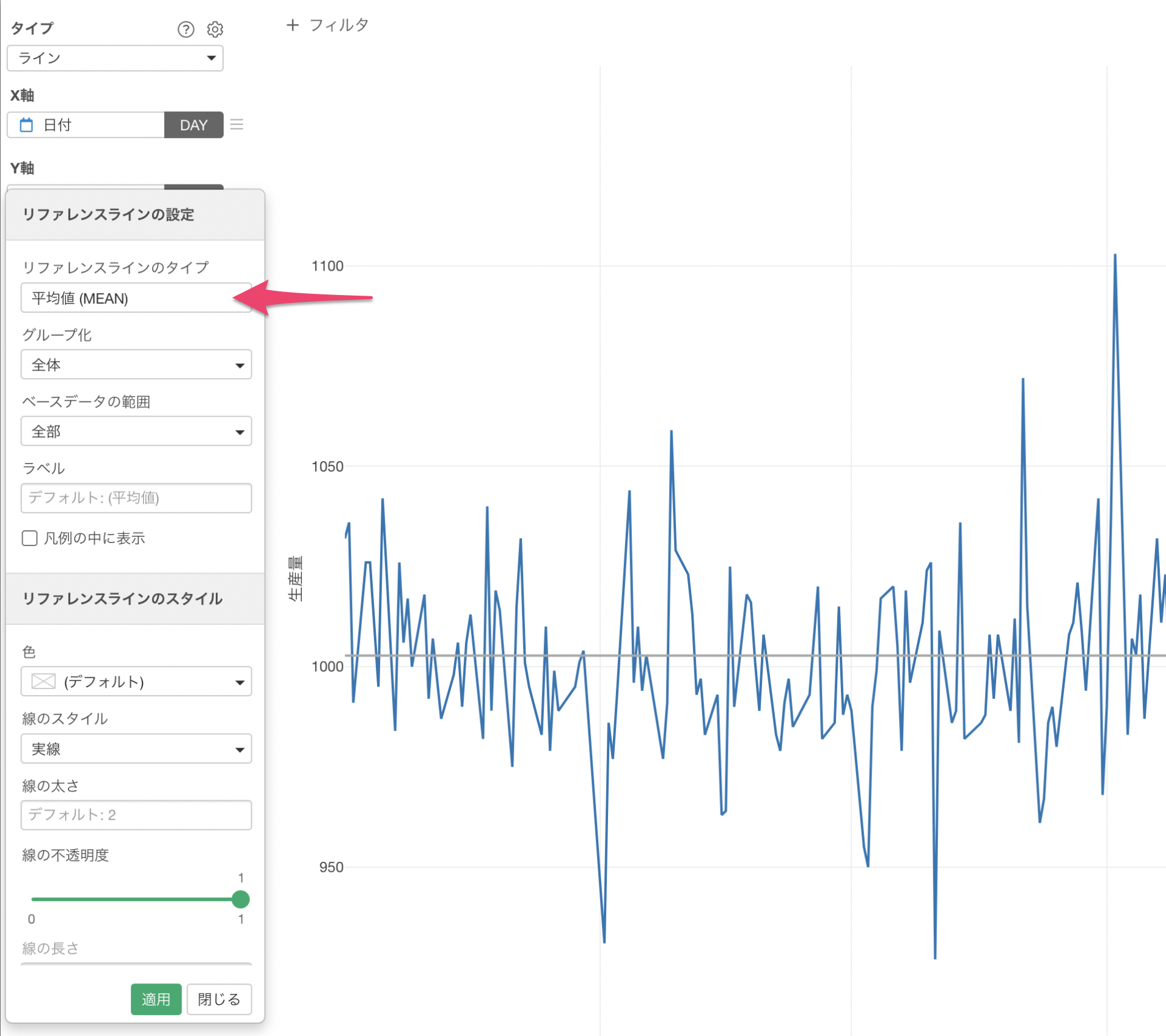
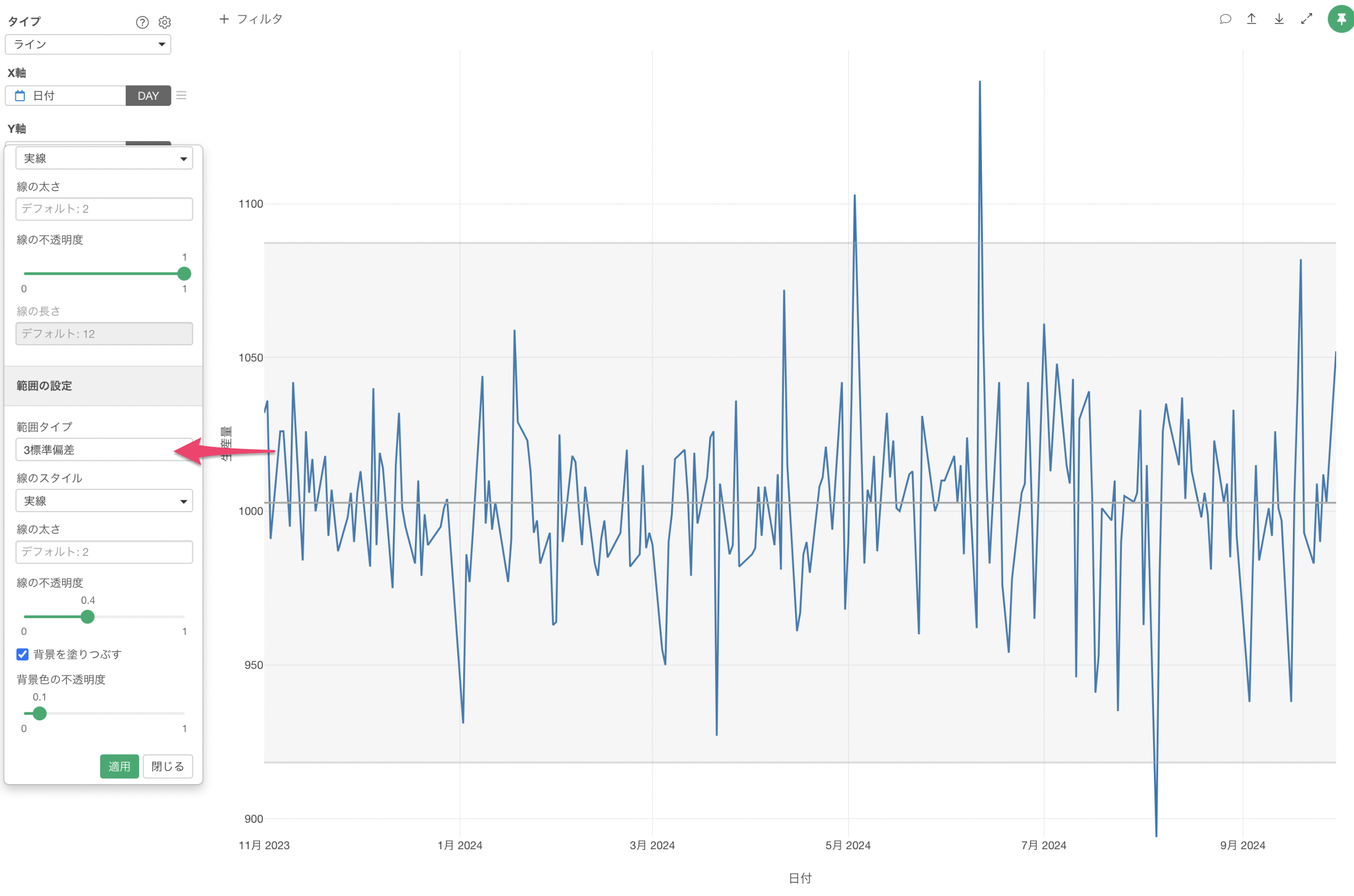
範囲タイプには「2標準偏差」を選択します。
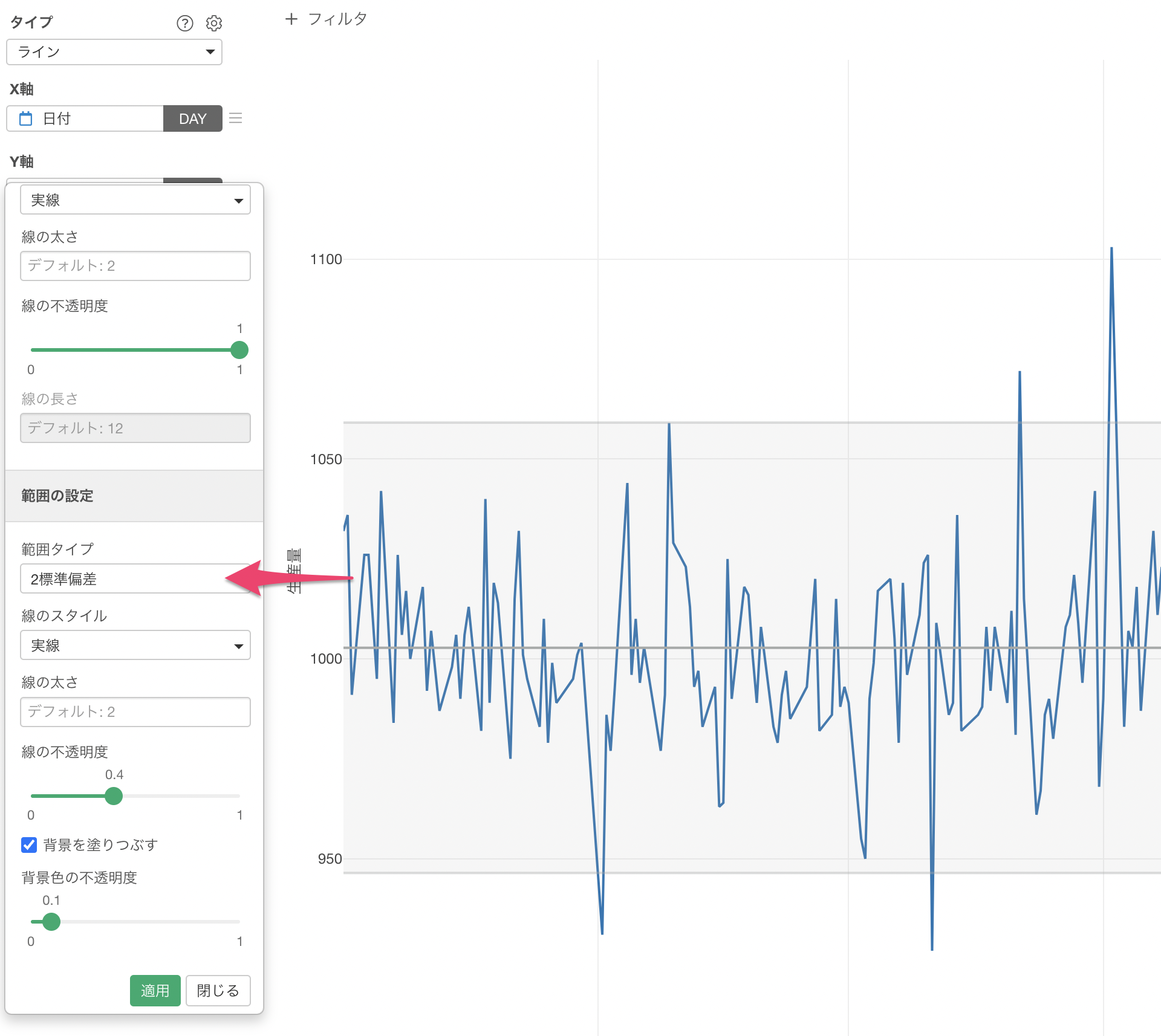
これによって2標準偏差を使って異常値検知を行うことができました。
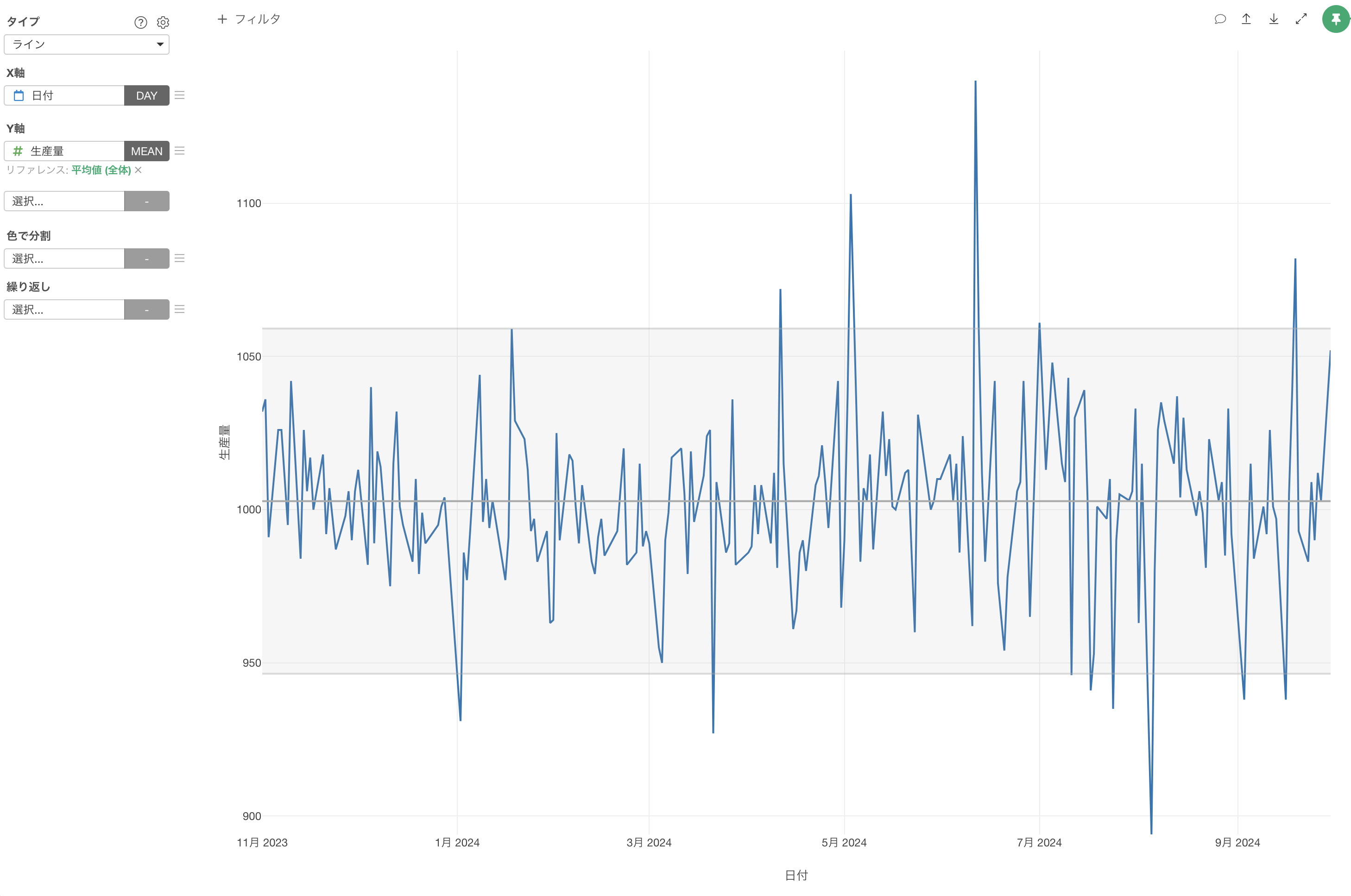
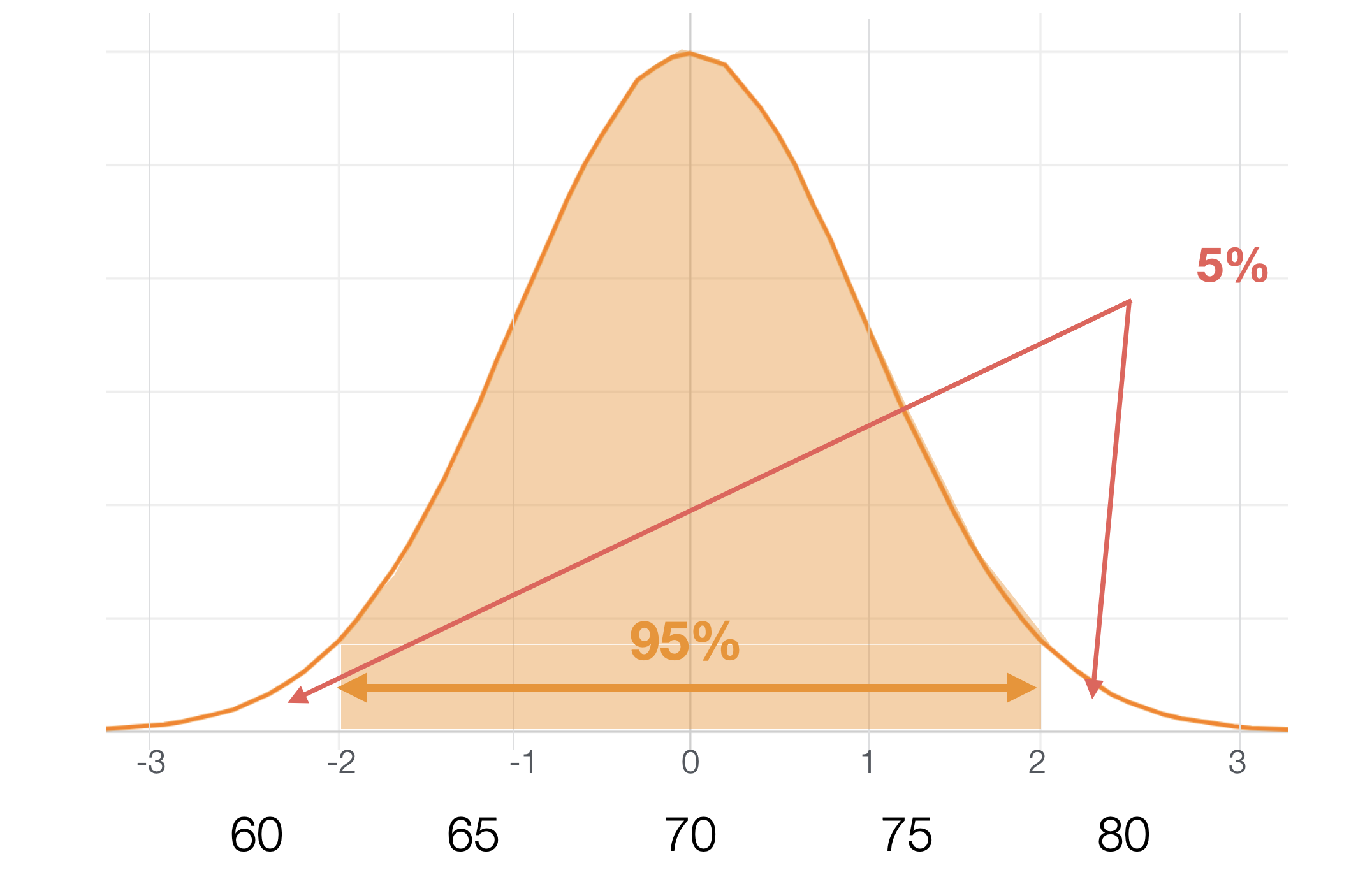
正規分布が前提となっている場合、2標準偏差の間に約95%の値が入ります。
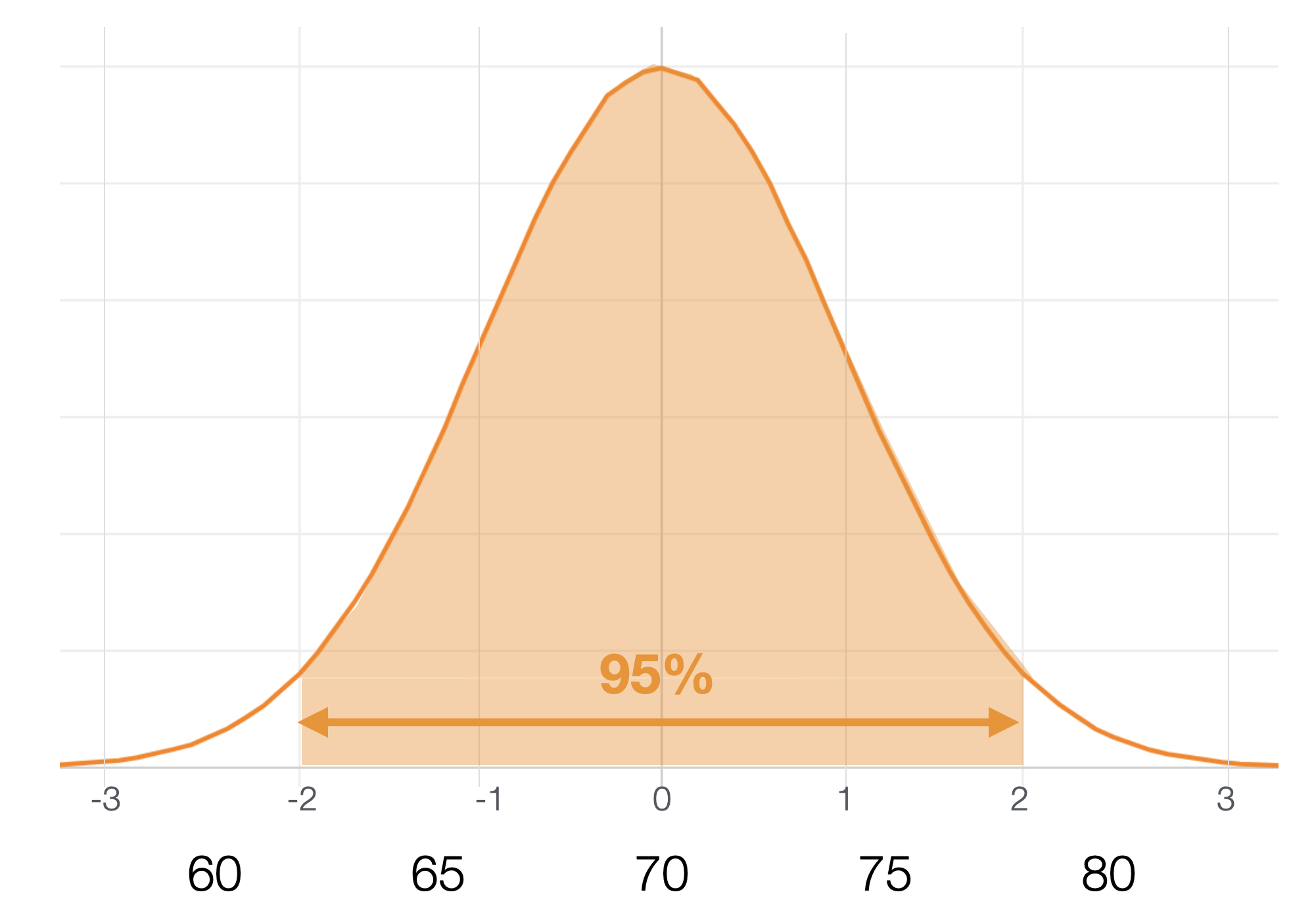
つまり、2標準偏差に入らない値は約5%となります。
さらに、平均値から標準偏差の3倍の範囲を使いたいため、範囲タイプに「3標準偏差」を選択します。
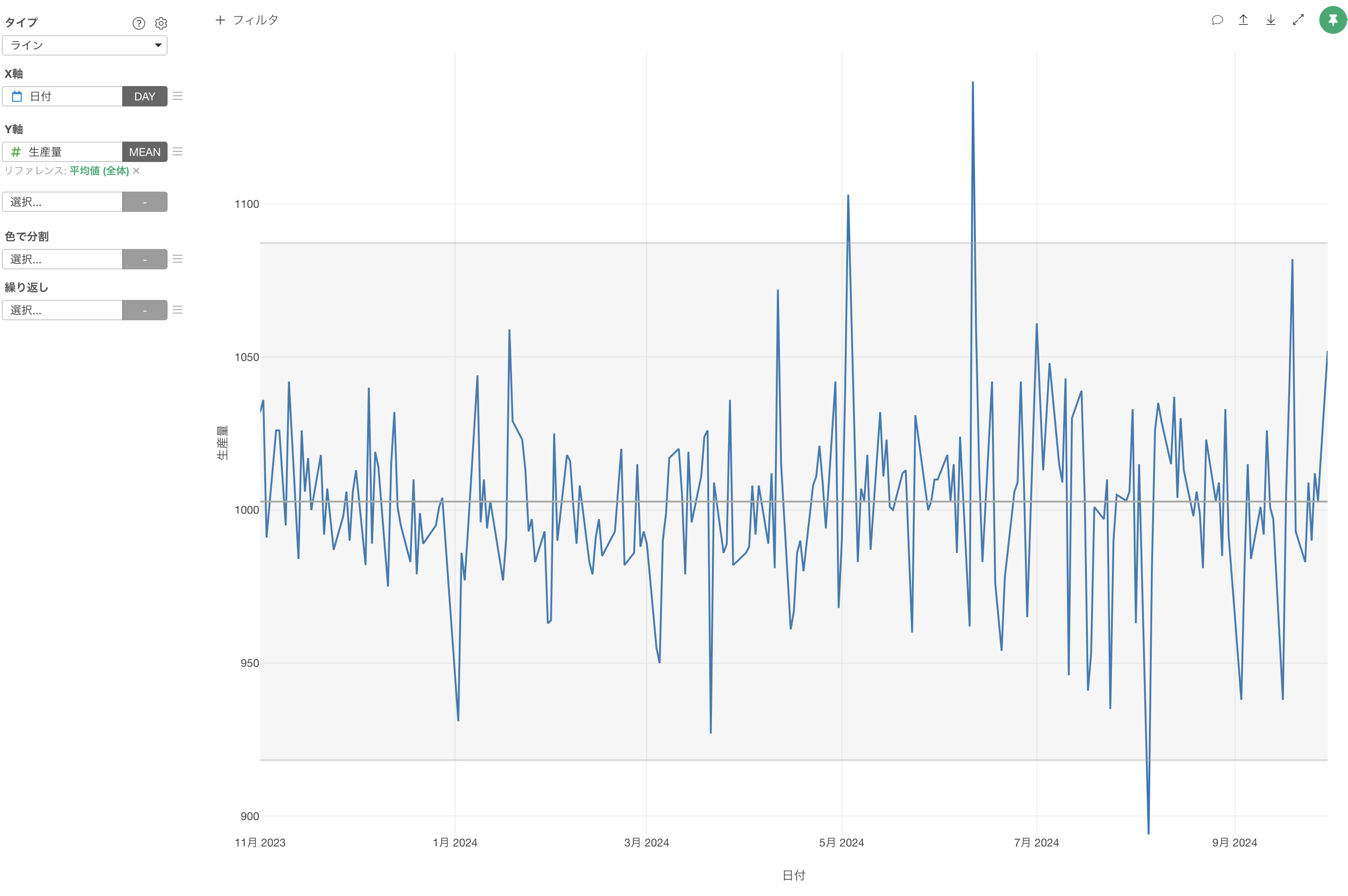
 これによって3標準偏差を使って異常値検知を行うことができました。
これによって3標準偏差を使って異常値検知を行うことができました。
正規分布が前提となっている場合、3標準偏差の間に約99.7%の値が入ります。
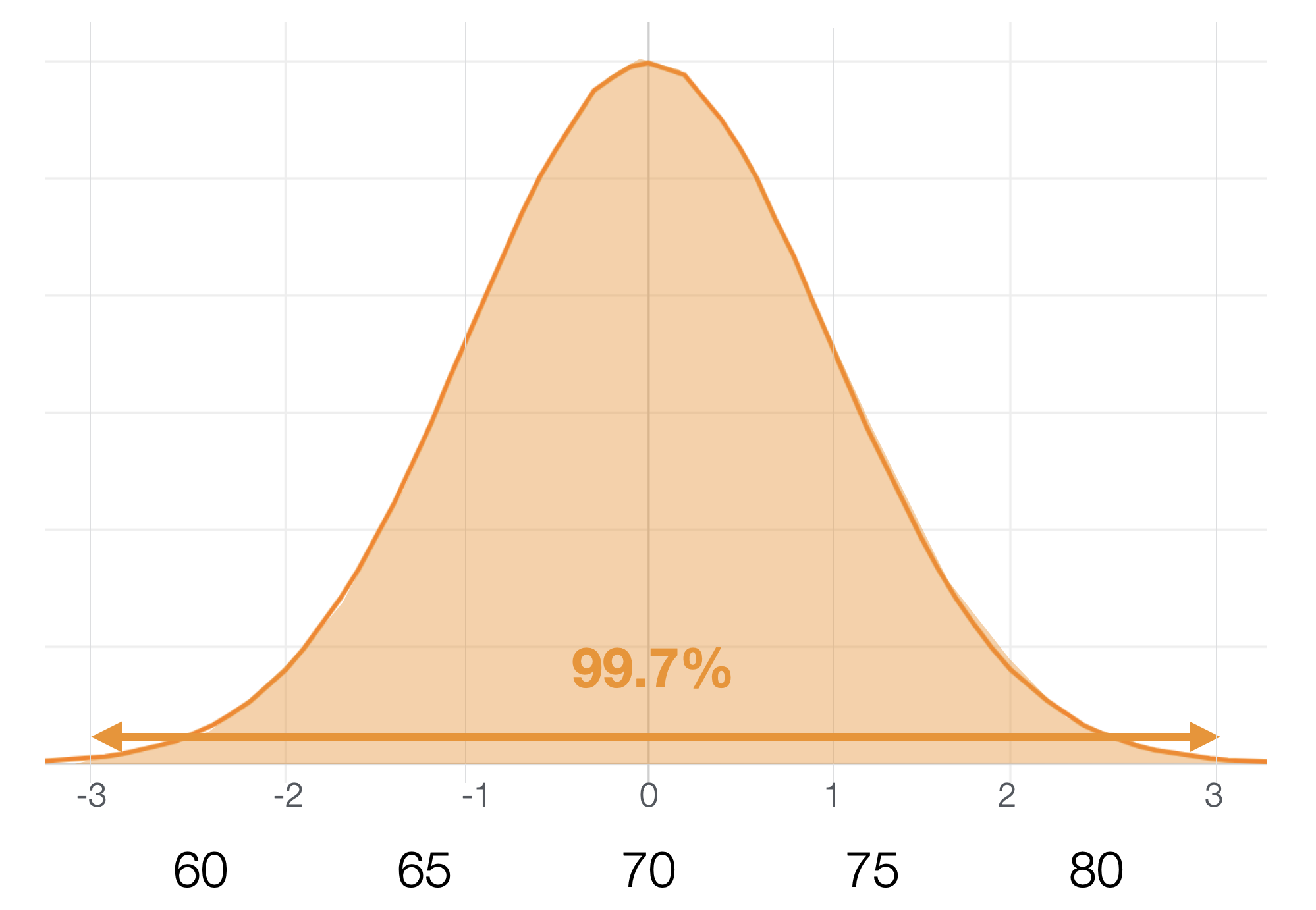
つまり、3標準偏差に入らない値は約0.3%となります。
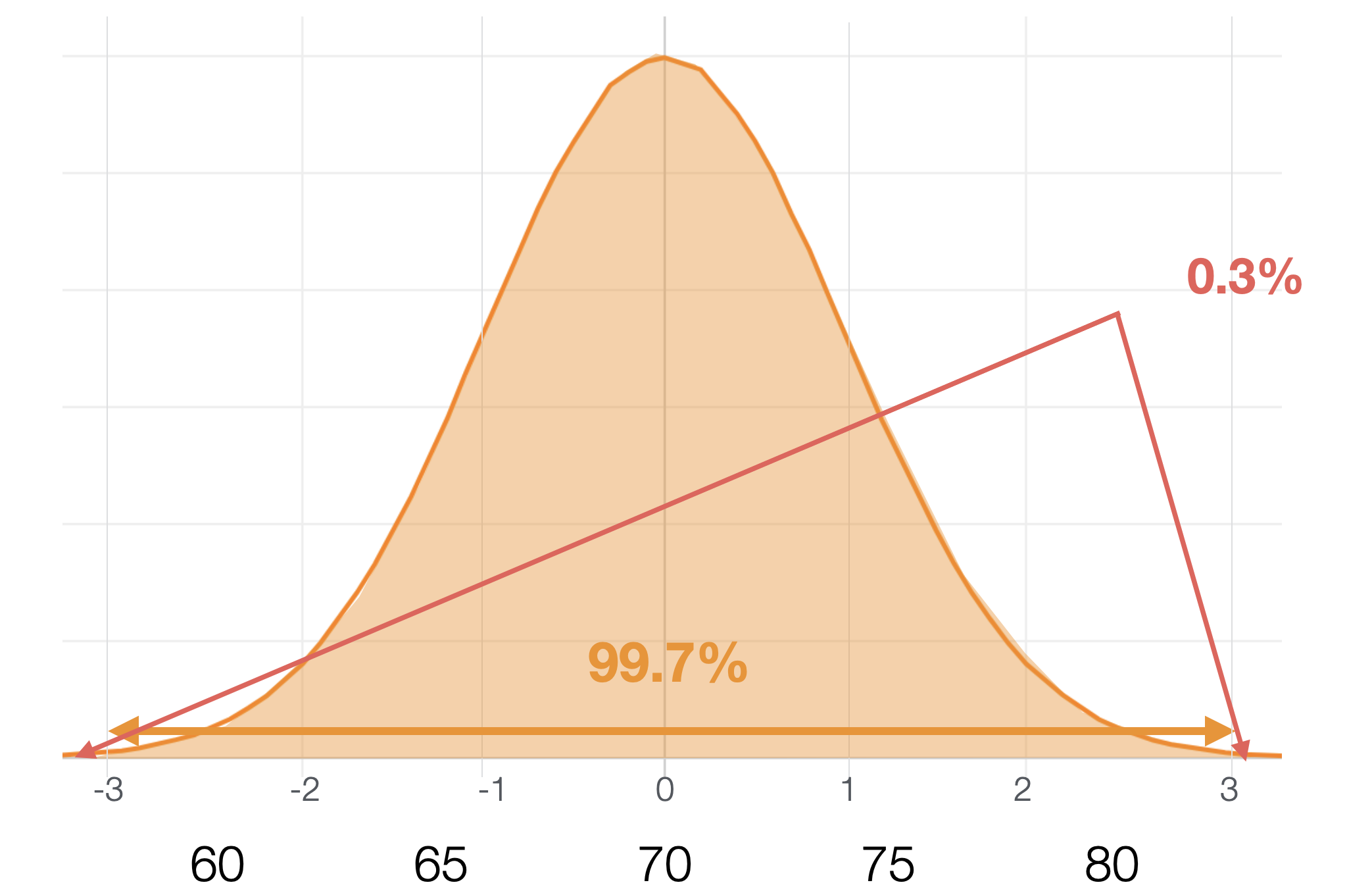
この範囲を超えるデータは異常値として判定され、即座な調査と対応が必要となります。この方法は、比較的シンプルで理解しやすい手法として知られています。
標準偏差での異常値検知の問題点
標準偏差による異常値検知には、いくつかの重要な制約があります。
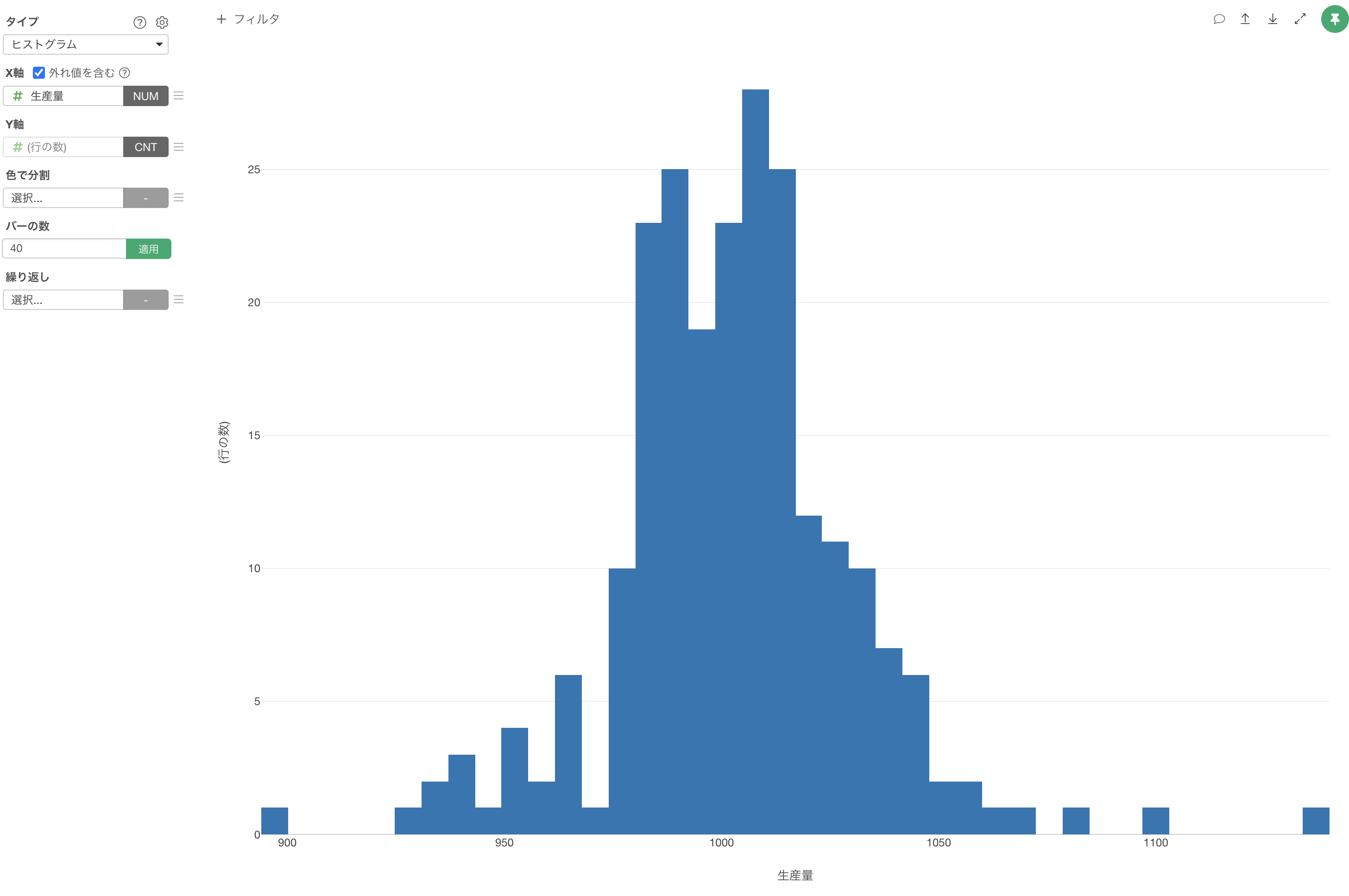
最も大きな問題は、データが正規分布に従うことを前提としている点です。実際のビジネスデータは、必ずしも正規分布に従わず、歪んだ分布や多峰性の分布を示すことが多く、そのような場合には誤った検知に繋がってしまいます。
今回のデータは以下のような分布の形になっています。
さらに、Exploratoryではアナリティクスビューにて「統計的検定」の中にある「正規繊維検定」を使うことで、その数値列が正規分布かどうかを確認することができます。
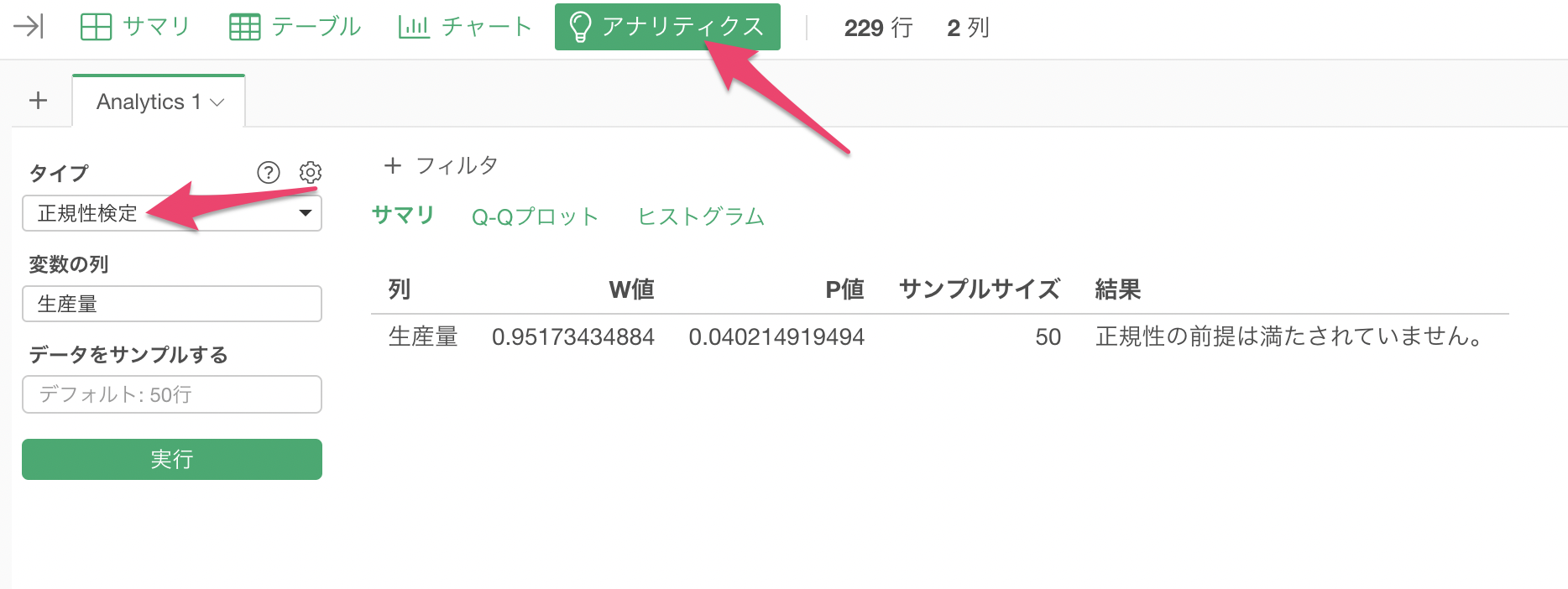
その結果このデータでは正規分布ではないということがわかりました。
また、この手法は外れ値の影響を強く受けるという特徴があります。異常値自体が平均値と標準偏差の計算に影響を与えてしまい、結果として標準偏差を使った時の範囲が異常に広くなってしまい、信頼性が低下してしまうことがあります。
XmRチャートを使った異常値検知
XmRチャートは、データの分布に依存しない異常値検知の手法として非常に有用です。
正規分布を前提としないため、様々な形状の分布に対して適用可能です。
実用面では、プロセスの変化を視覚的に把握できる点が大きな利点です。さらに、少量のデータでも適用可能で、リアルタイムモニタリングにも適しているため、様々な業種やプロセスでの応用が可能です。
XmRチャートは、個々の測定値(X)のチャートと移動範囲(mR)のチャートという2つの要素で構成されています。XmRチャートの具体的な計算式については、こちらをご覧ください。
XmRチャートを使って異常値検知をするために、範囲タイプに「管理限界(X)」を選択します。
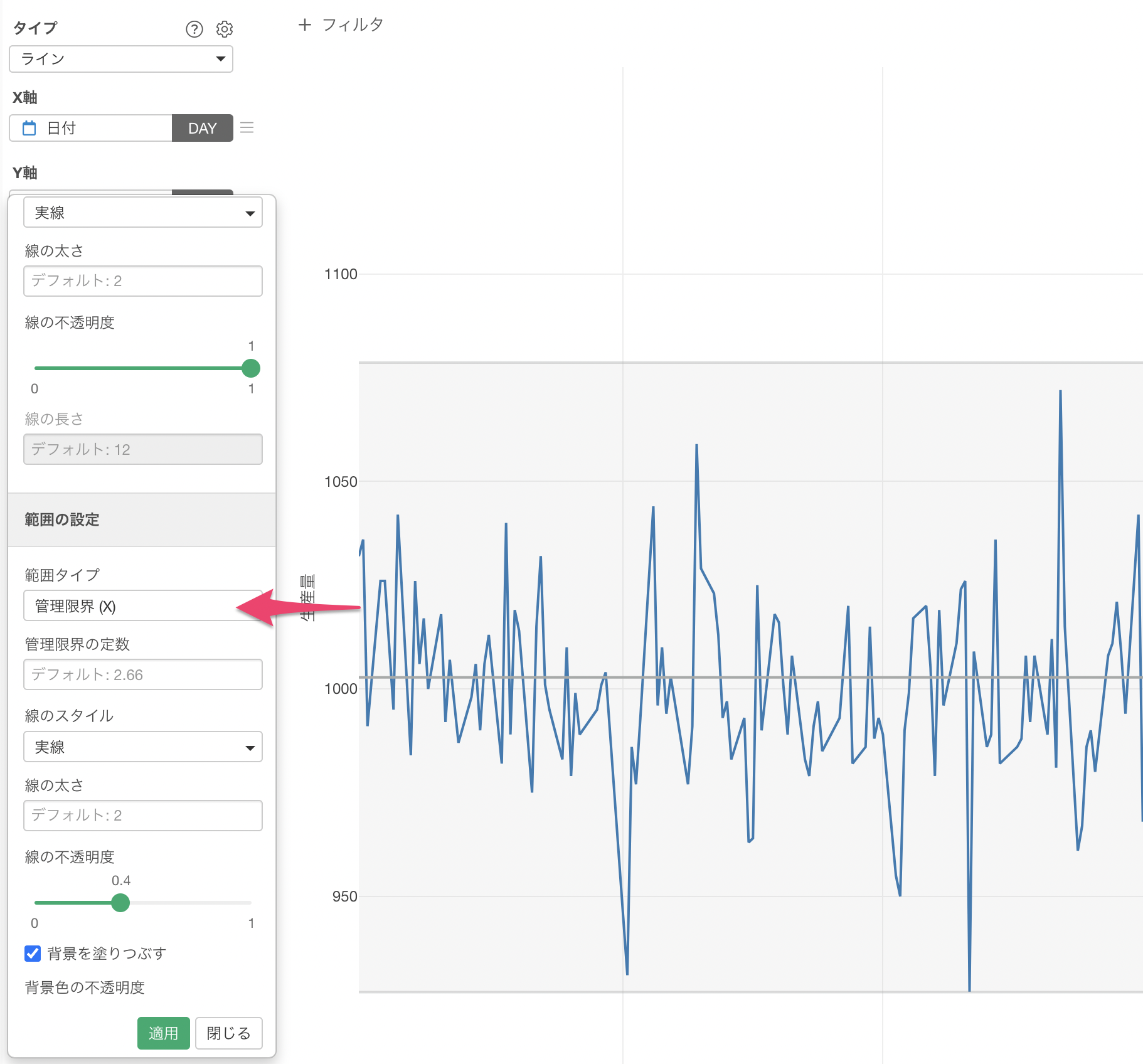
これによってXmRチャートを使って異常値検知を行うことができました。XmRチャートの場合は、データが正規分布であるという前提もないために、どういったデータでも使用することができるようになっています。
XmRチャートでシグナルかどうかを判断するための3つのルール
XmRチャートを使ってシグナルかどうかを判断する際には、以下の3つのルールがあります。
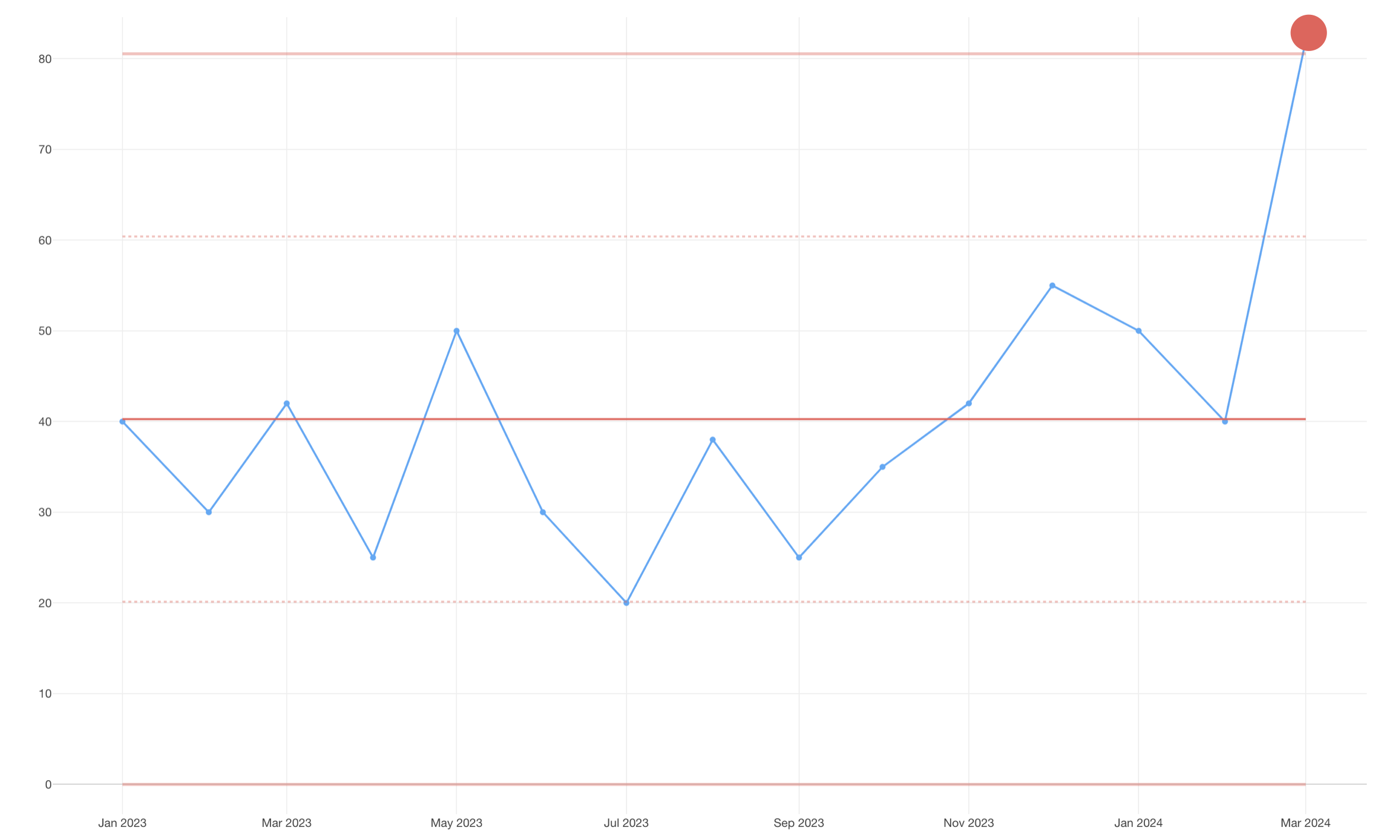
ルール 1: 値が管理限界の外にあるとき
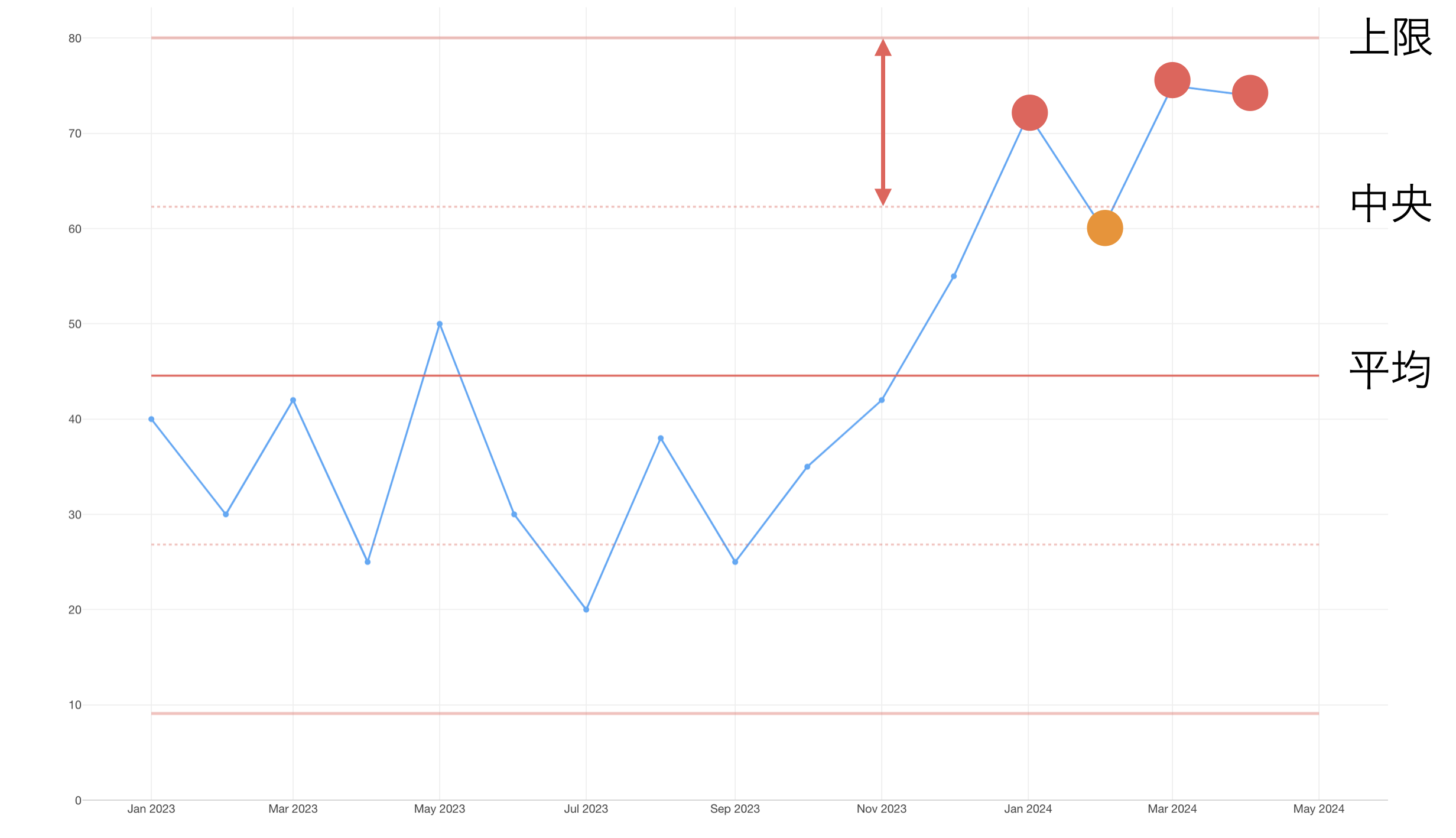
ルール 2: 連続した4つの値のうち3つが平均よりも上限(または下限)に近いとき
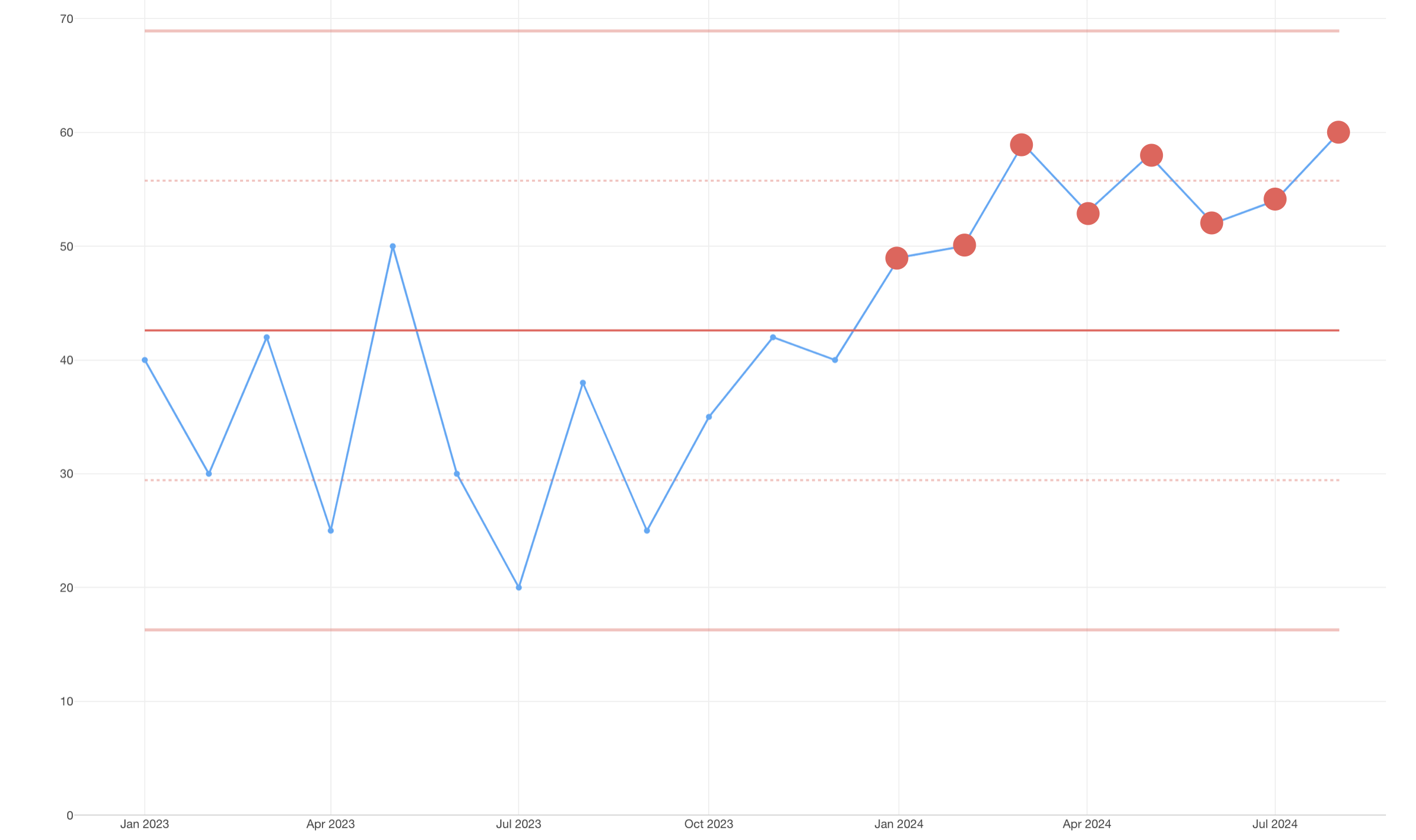
ルール 3: 平均の上側(または下側)に連続して8つの値が並んだとき。
上記の3つのルールのうち、どれかに該当する場合はその値はシグナルであると判断し、何が要因になっているのか調査する必要があります。