Two-Way ANOVA（分散分析）の使い方
Two-Way ANOVA（二元配置分散分析）は、2つの異なる要因（独立変数）が1つの結果（従属変数）にどのように影響を与えているかを分析する手法です。この分析では、各要因の主効果だけでなく、2つの要因間の交互作用も検証することができます。例えば、年齢層と性別という2つの要因が購入金額にどのように影響を与えているのかを分析する際、年齢層による影響、性別による影響、そしてそれらの組み合わせによる特有の影響（交互作用）を同時に評価することができます。
Two-Way ANOVAの特徴的な点は、2つの要因の組み合わせによる相乗効果や打ち消し合う効果を発見できることです。例えば、一般的に年齢層が上がるほど購入金額が増加する傾向がある一方で、その増加パターンが性別によって異なるといった複雑な関係性を明らかにすることができます。これにより、単純な一要因の分析では見落としてしまう可能性のある重要なパターンや関係性を特定することが可能となります。
この分析手法の最大の利点は、複数の要因を同時に分析できることに加えて、それぞれの要因の効果の大きさを統計的に比較できる点にあります。例えば、購入金額の変動に対して年齢層と性別のどちらがより大きな影響を持っているのかを定量的に評価できます。また、交互作用の有無を確認することで、より効果的なマーケティング戦略の立案や、商品開発の方向性の決定など、実務的な意思決定に直接活用できる知見を得ることができます。
1. どういった時に使えるのか
Two-Way ANOVAは、2つのカテゴリカルな要因が数値データにどのように影響を与えているかを理解したい場合に特に有効です。例えば、ECサイトでの商品の売れ行きを分析する際、商品カテゴリーと販売チャネルという2つの要因が売上金額にどのように影響しているかを分析できます。また、教育分野では、教授法と学習環境が学生の成績にどのように影響するかを調査する際にも活用できます。
ビジネスの現場では、新商品の開発やマーケティング戦略の立案時に、複数の要因の効果を同時に検証する必要がある場合に特に重宝します。例えば、広告の効果を測定する際に、広告の種類と表示時間帯という2つの要因が、クリック率にどのように影響するかを分析することができます。また、顧客満足度調査では、サービスの種類と顧客の属性が満足度にどのように影響するかを理解するのに役立ちます。
参考となるデータ例：
- 商品カテゴリー×販売チャネル別の売上データ
- 年齢層×性別による商品購入金額データ
- 広告タイプ×配信時間帯別のコンバージョン率データ
- 教育方法×学習環境別の学習成績データ
2. ユースケース
EC事業での使い方
- ECサイトでは、商品カテゴリーと購入チャネルの組み合わせが購入金額に与える影響を分析する時に使えます。
- 具体的には、商品カテゴリー（食品、衣類、電化製品など）と購入チャネル（PC、スマートフォン、タブレット）の組み合わせが、顧客の購入金額にどのように影響するかを分析することで、各チャネルでどの商品カテゴリーが強いのかがわかるようになります。
- これにより、各チャネルでの商品の見せ方や、重点的にプロモーションを行うカテゴリーを決定する際のヒントとなります。
教育サービスでの使い方
- 教育サービスでは、指導方法と学習時間帯の組み合わせが学習効果に与える影響を分析する時に使えます。
- 具体的には、指導方法（対面、オンライン、ハイブリッド）と学習時間帯（午前、午後、夜間）の組み合わせが、テストスコアにどのように影響するかを分析することで、最も効果的な学習環境を特定できるようになります。
- これにより、時間帯別の最適な指導方法の選択や、カリキュラムの改善といった施策を打つ際のヒントとなります。
マーケティング担当者での使い方
- マーケティング担当者は、広告タイプと配信プラットフォームの組み合わせが広告効果に与える影響を分析する時に使えます。
- 具体的には、広告タイプ（動画、バナー、テキスト）と配信プラットフォーム（SNS、検索連動型、ディスプレイ）の組み合わせが、コンバージョン率にどのように影響するかを分析することで、最も効果的な広告戦略を把握できるようになります。
- これにより、予算配分の最適化や、プラットフォーム別の広告クリエイティブ戦略を立案する際のヒントとなります。
商品開発担当者での使い方
- 商品開発担当者は、製品機能と価格帯の組み合わせが顧客満足度に与える影響を分析する時に使えます。
- 具体的には、製品機能（基本機能、プレミアム機能）と価格帯（エントリー、ミドル、ハイエンド）の組み合わせが、顧客満足度にどのように影響するかを分析することで、最適な製品ラインナップを特定できるようになります。
- これにより、新製品の機能設計や価格設定を決定する際のヒントとなります。
3. ExploratoryでTwo-Way ANOVAを実行する
使用するデータ
今回は「小売業顧客購買データ」を使用します。データはこちらからダウンロードが可能となっています。
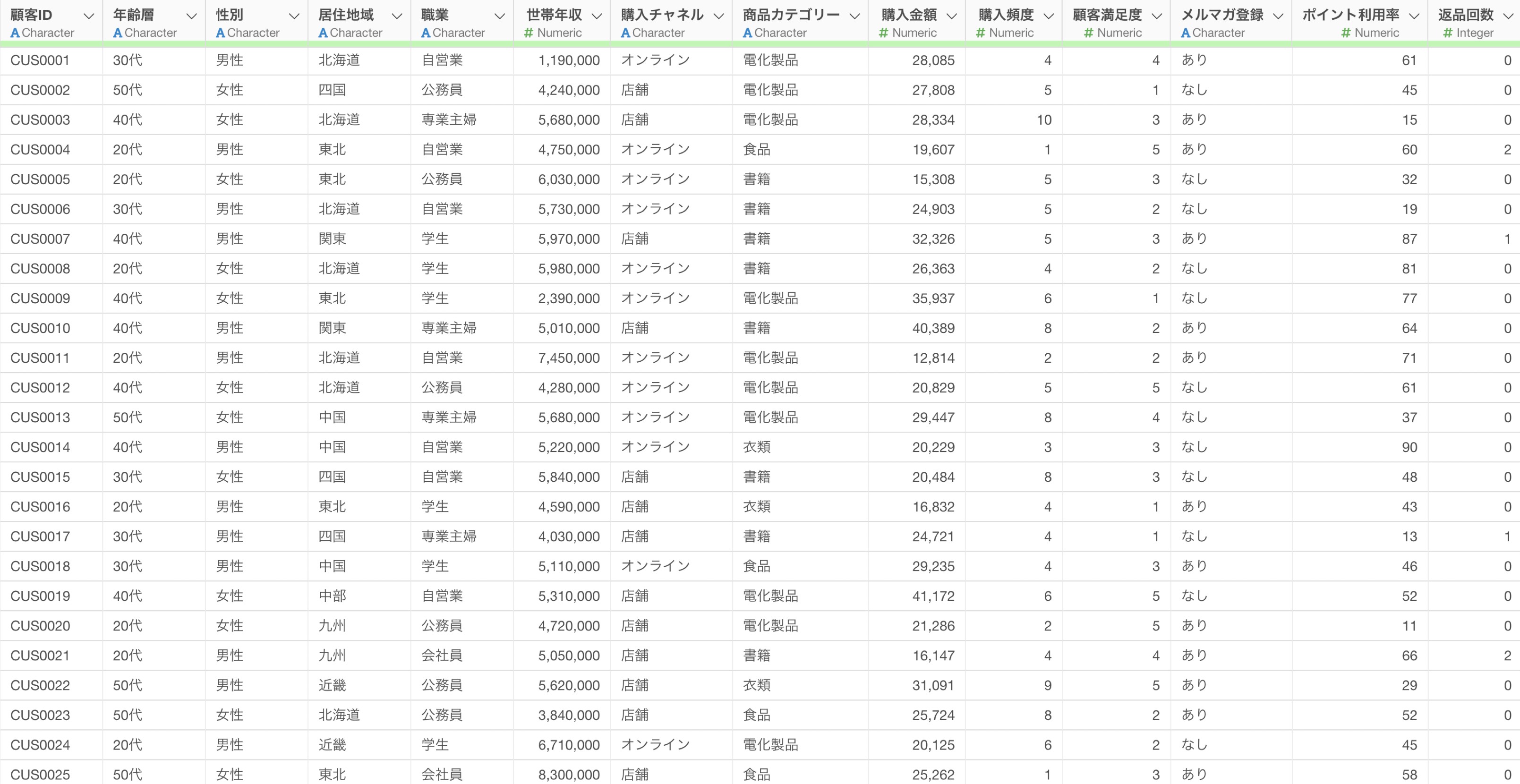
このデータは小売業の顧客購買データで、1行が1顧客の購買情報で、列には顧客ID、年齢層、性別などの属性情報に関するデータがあります。
Two-Way ANOVAを作るためには、以下のようなデータの構造が必要となります。
- 1つの数値型の目的変数（分析対象となる変数）
- 2つのカテゴリ型の変数（要因）
- 各カテゴリの組み合わせに十分なサンプル数があること
- データに極端な外れ値が含まれていないこと
アナリティクスを作成する
小売業顧客購買データから「アナリティクス・ビュー」を開きます。
タイプに「統計的検定」を選び、「Two-Way ANOVA (分散分析)」を選択します。
目的変数には、「購入金額」の列を割り当てます。
説明変数1には「年齢層」を、説明変数2には「性別」を割り当てます。
最後に、「実行」ボタンをクリックして実行結果を確認します。
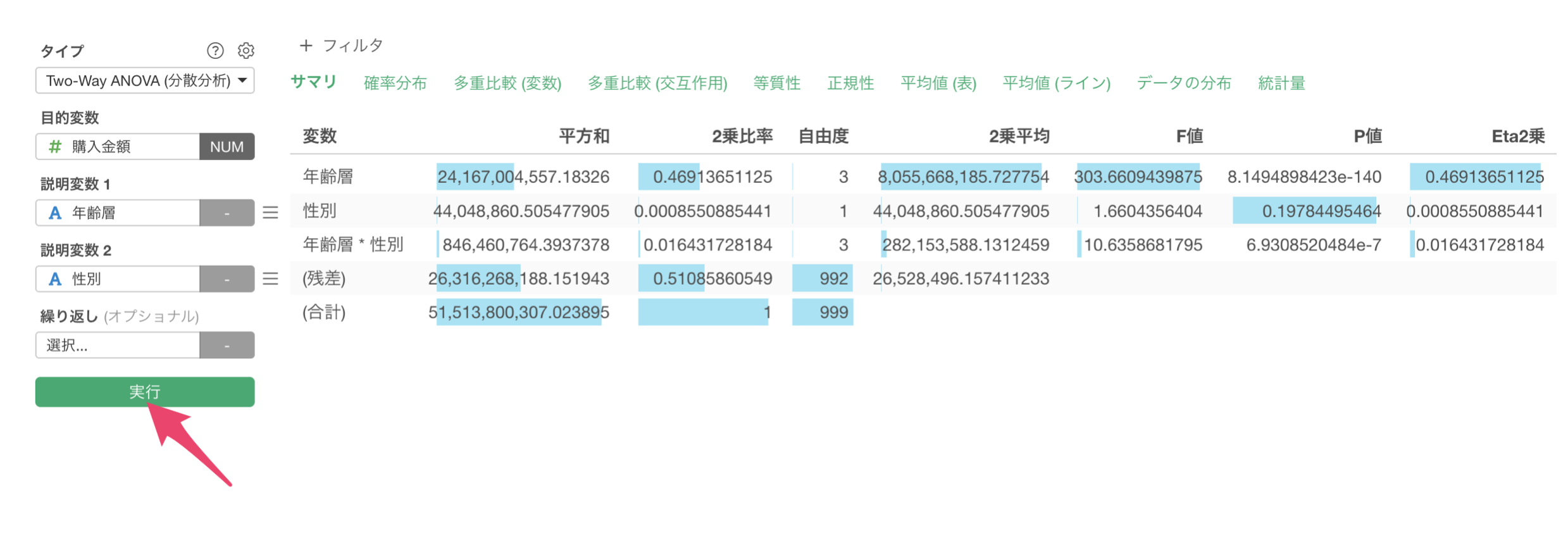
結果の解釈
Two-Way ANOVAでは、年齢層と性別が購入金額に与える影響を解釈するためにサマリや確率分布、多重比較などの情報があります。
サマリ
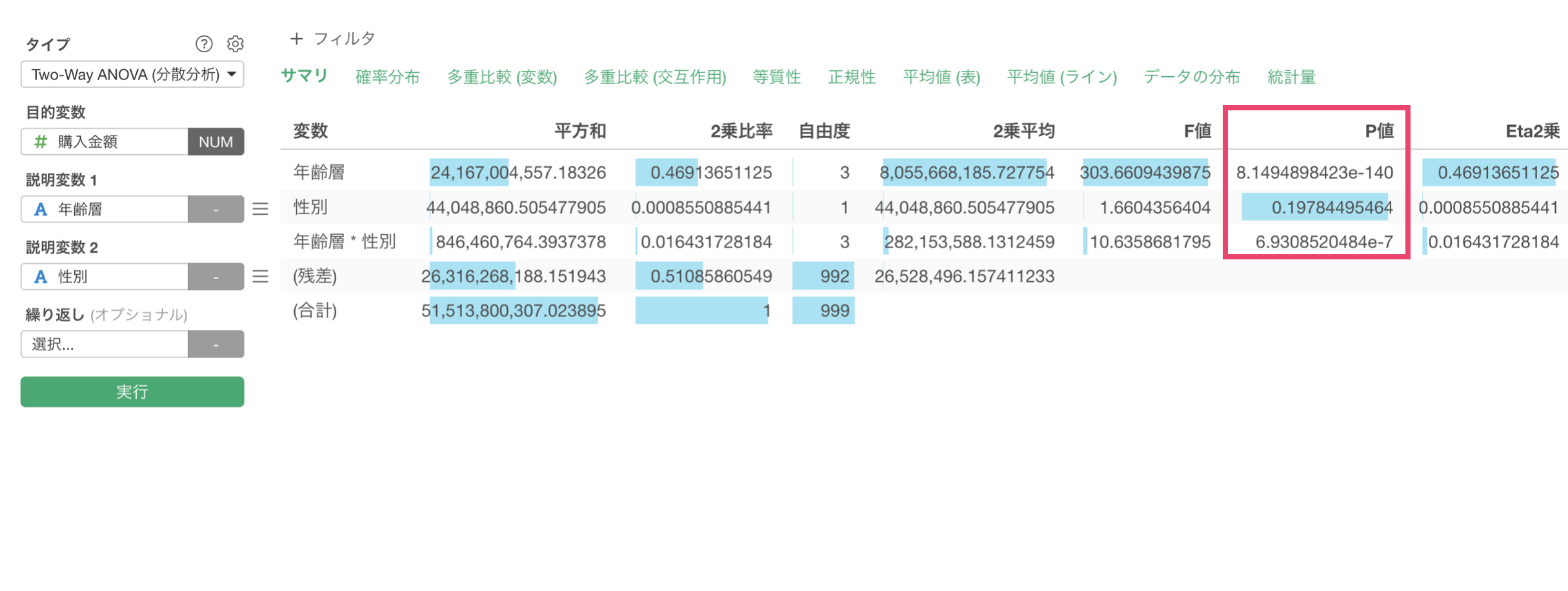
「サマリ」タブでは分散分析の基本的な結果を確認できます。
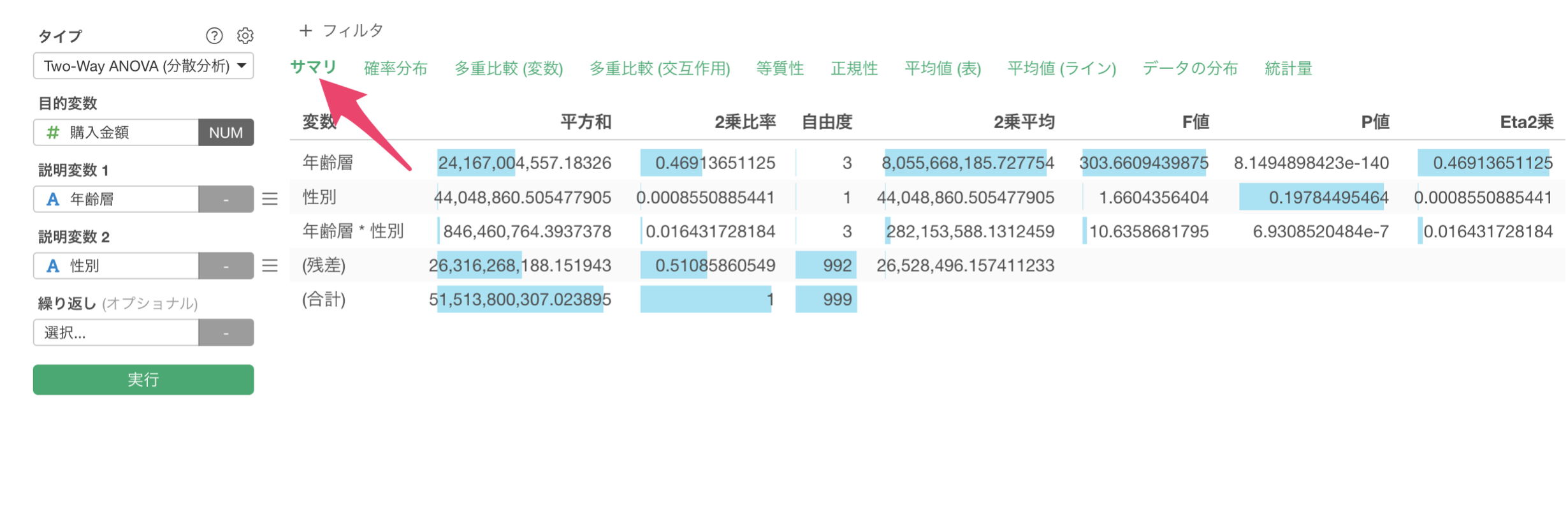
年齢層、年齢層と性別の組み合わせはP値が0.05未満のため、統計的に有意な差があることがわかります。一方で、性別単体ではP値が0.197（20%程度）で統計的に有意であるとは言えない結果となっています。
確率分布
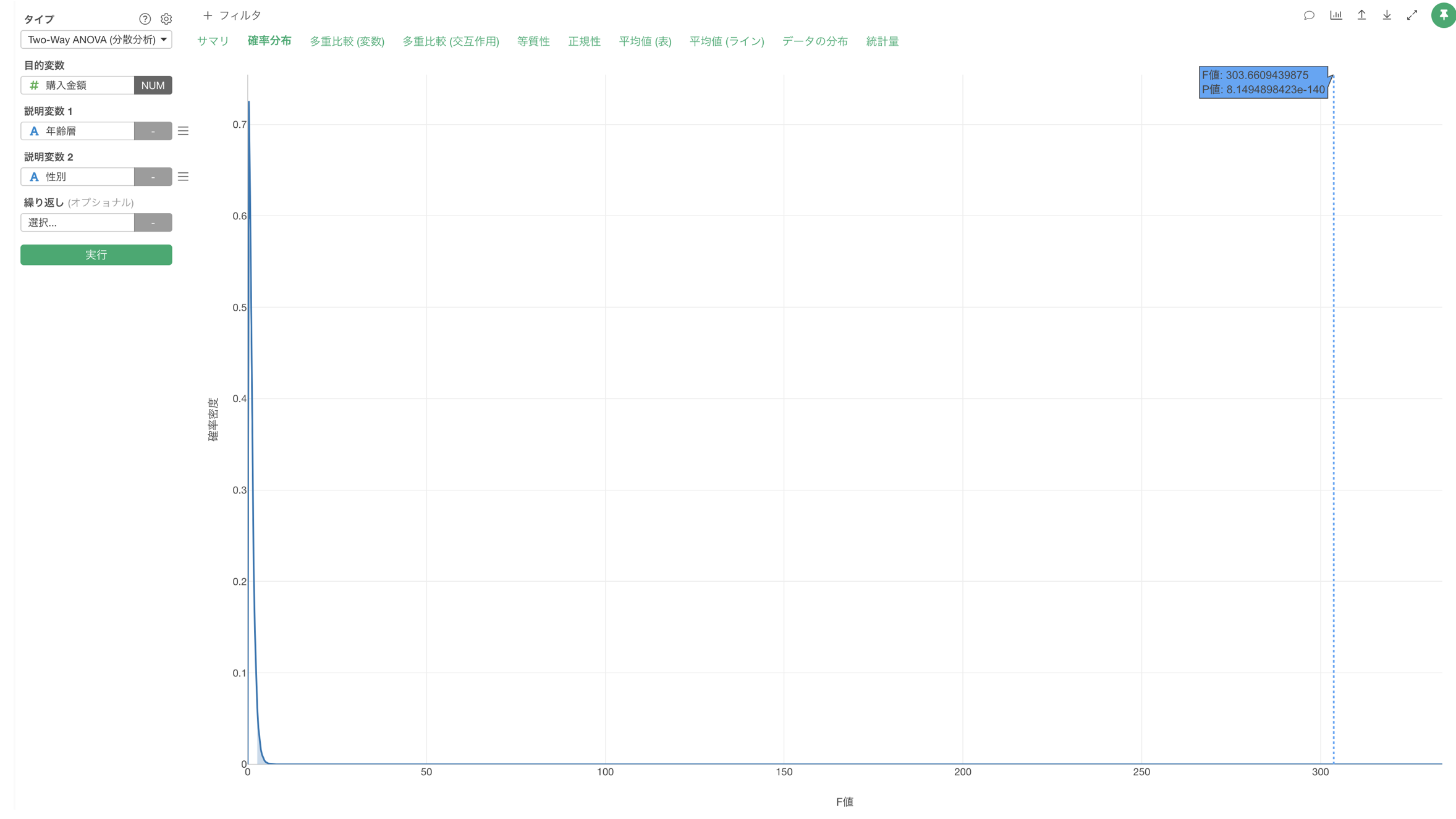
「確率分布」をクリックすると、F分布上での検定統計量の位置を確認することができます。
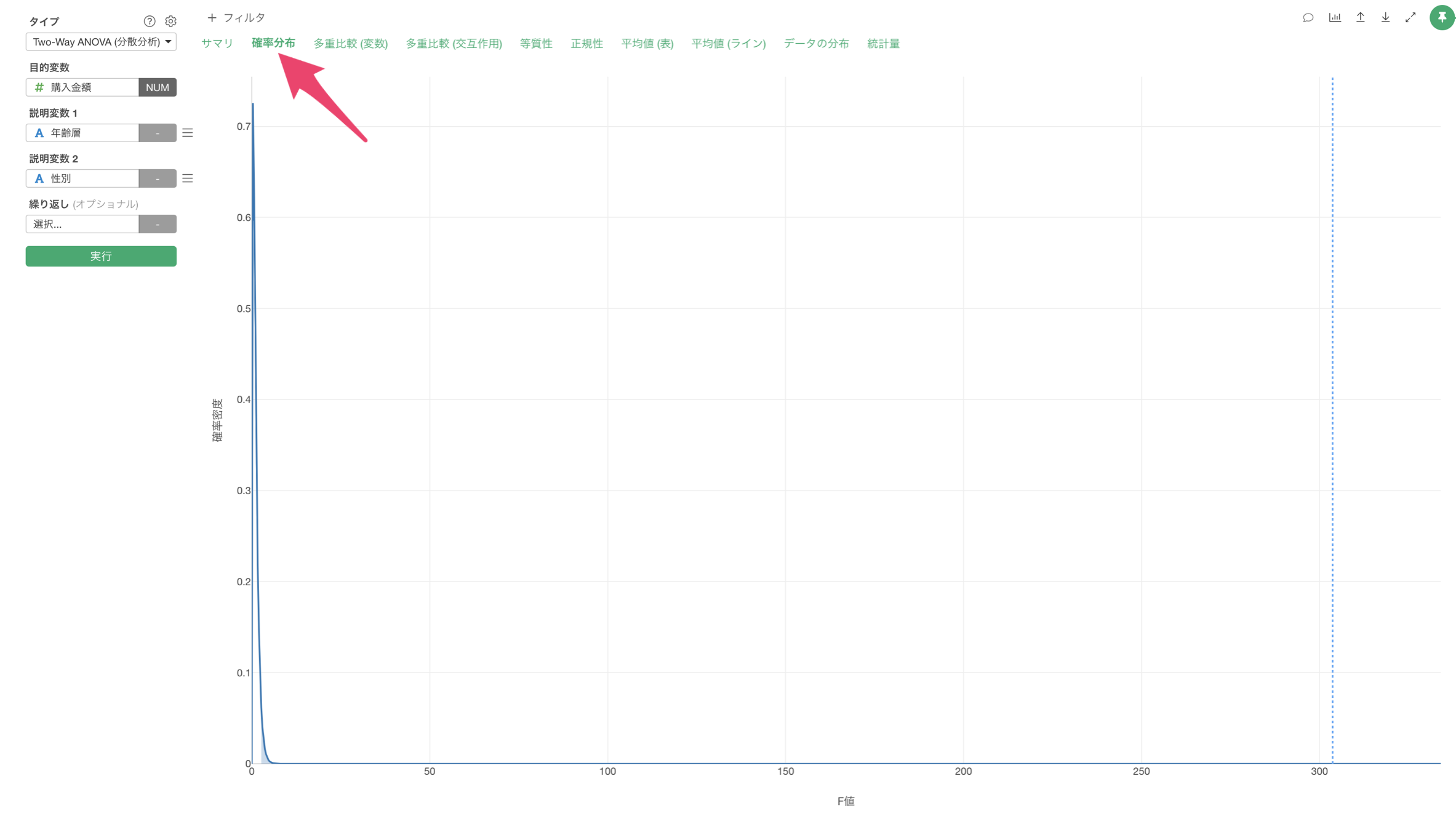
この結果から、観測されたF値が棄却域に入っているため帰無仮説を棄却でき、統計的に有意であると判断できます。
多重比較 (変数)
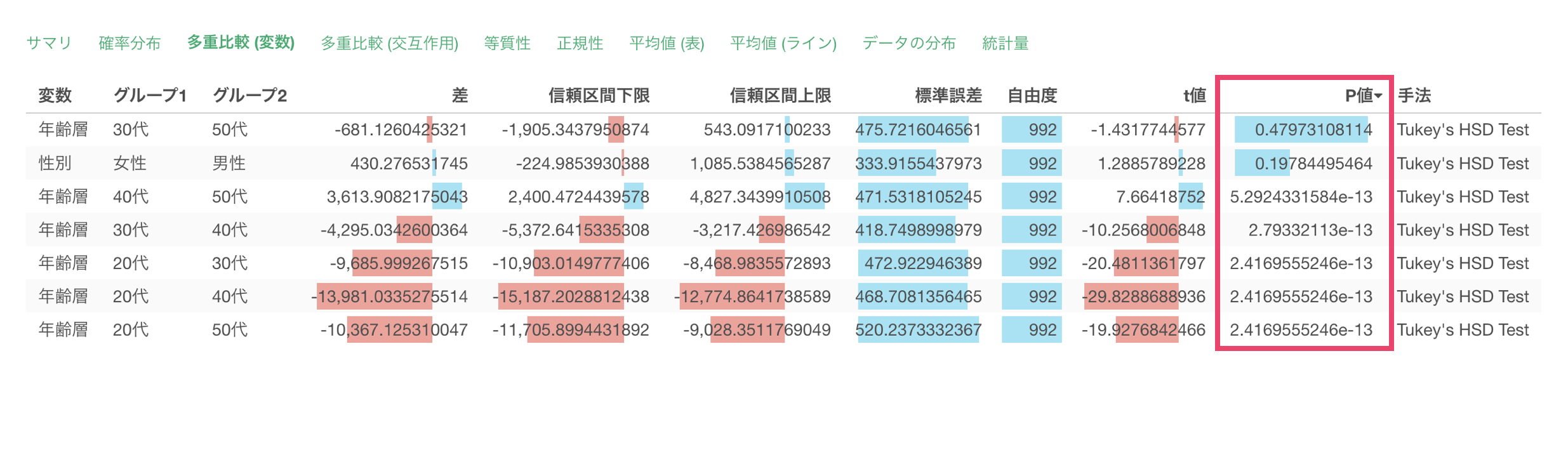
「多重比較 (変数)」をクリックすると、各年齢層間、性別間での購入金額の差の統計的有意性を確認することができます。
例えば、20代の購入金額は他のすべての年齢層と比較して有意に低く（P値は2.42e-13）、特に40代との差が最も大きく約14,000円の差があることがわかります。
多重比較 (交互作用)
「多重比較 (交互作用)」をクリックすると、年齢層と性別の組み合わせによる購入金額の差の統計的有意性を確認することができます。
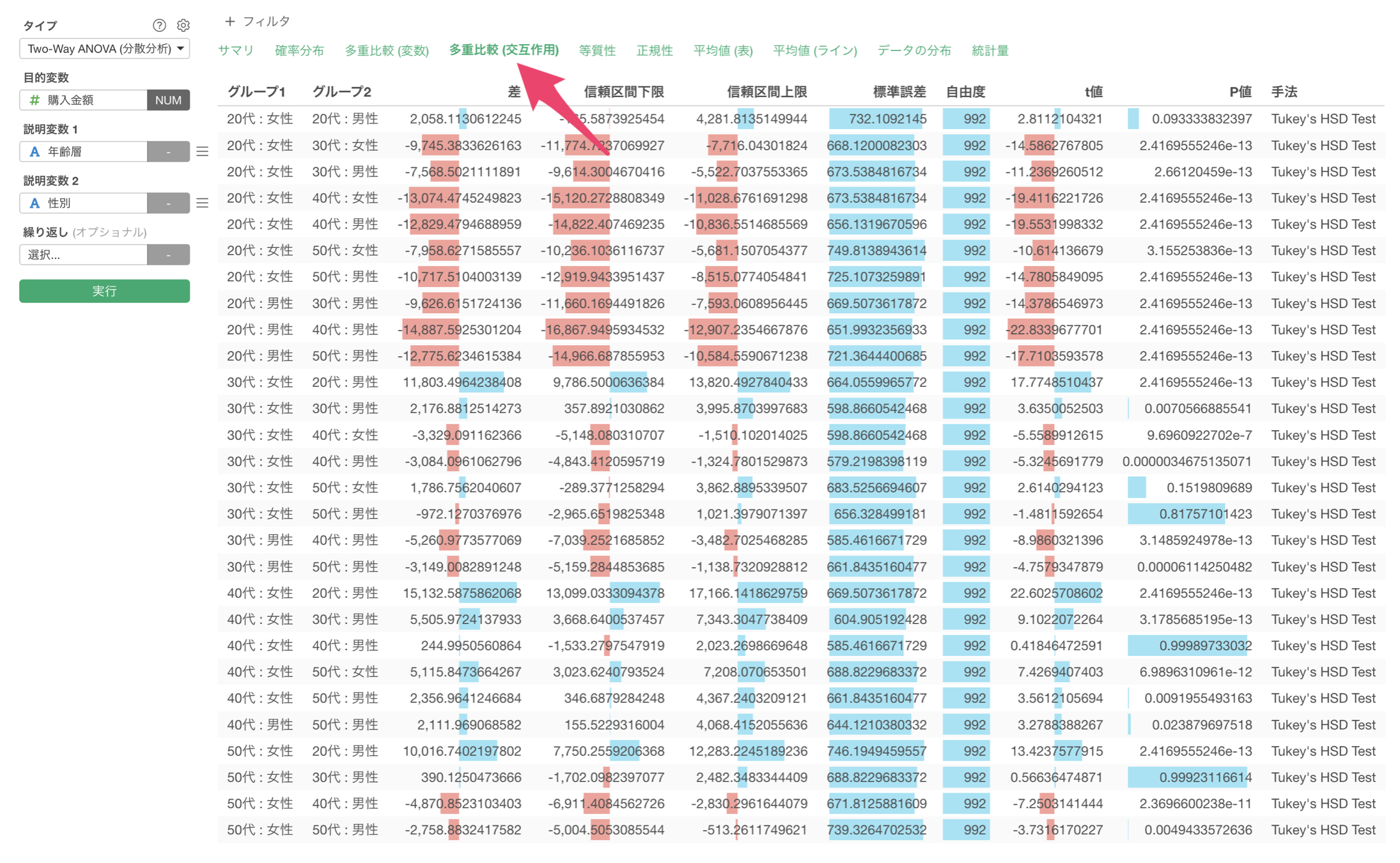
例えば、40代女性は他のほとんどの年齢・性別グループと比較して有意に高い購入金額を示しており、特に20代男性との差が最も大きく約15,130円の差があることがわかります。
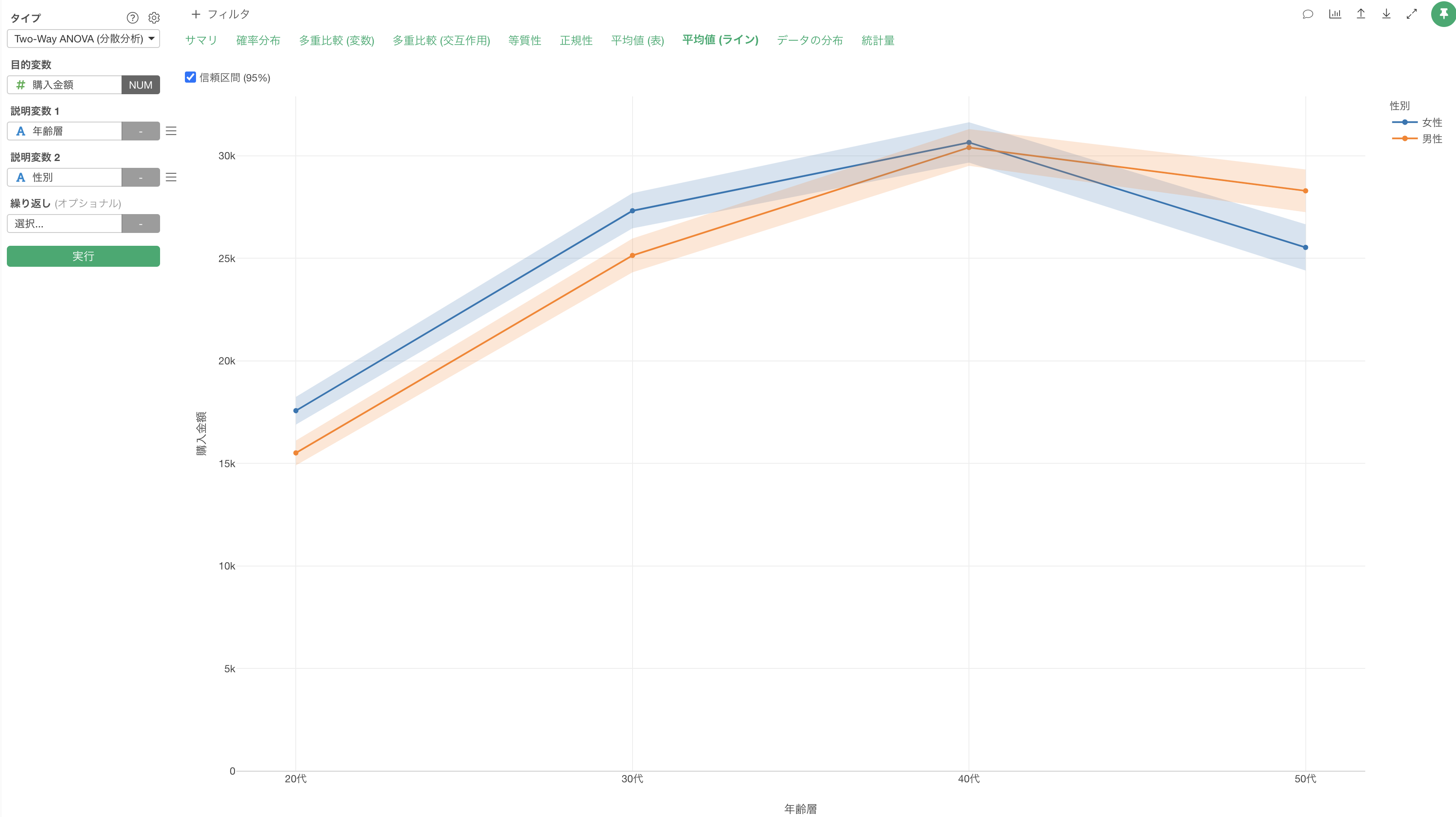
平均値 (ライン)
「平均値 (ライン)」をクリックすると、各要因の水準ごとの購入金額の平均値をラインで確認することができます。
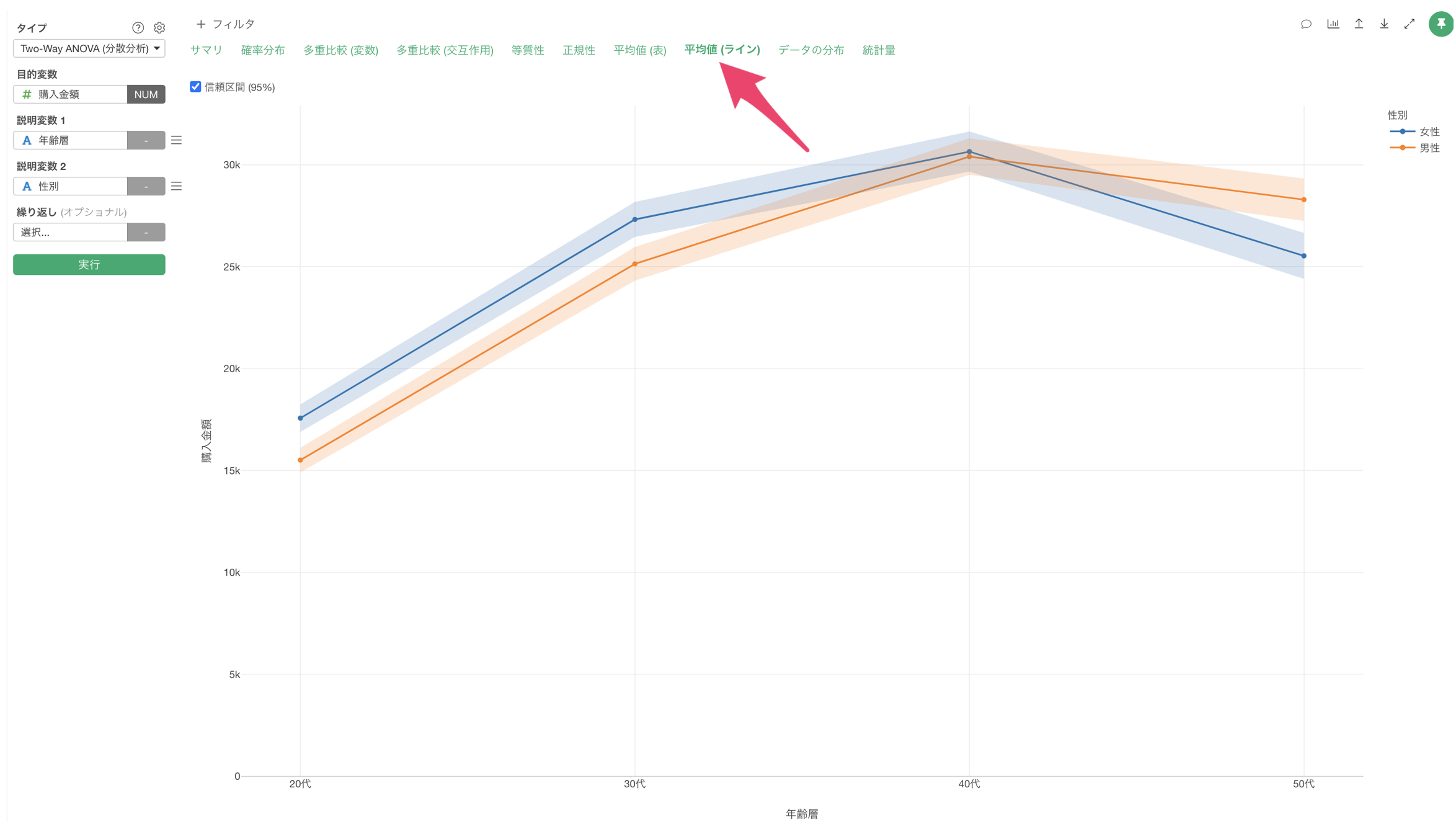
購入金額は両性別とも40代でピークを迎え、女性の方が全年齢層で購入金額が高い傾向を示していることが確認できます。
4. まとめ
Two-Way ANOVAは、2つのカテゴリカルな要因が数値データに与える影響を包括的に分析できる強力な手法です。今回の分析例では、年齢層と性別という2つの要因が購入金額に与える影響を検証し、それぞれの主効果だけでなく、要因間の交互作用も明らかにすることができました。特に、30代・40代の女性が重要な顧客セグメントであることが統計的に示され、このような知見は効果的なマーケティング戦略の立案に直接活用することができます。