一般化線形モデル - GLM - ポアソン分布の使い方

一般化線形モデル（GLM）のポアソン分布は、カウントデータ（発生回数や件数）を分析する際に使用される統計手法です。通常の線形回帰では負の値や小数点を予測する可能性がありますが、ポアソン回帰では0以上の整数値のみを予測対象とします。これは顧客の購買回数、問い合わせ件数、事故発生件数など、カウントデータの特性に適した分析手法となります。

ポアソン分布の特徴として、平均値と分散が等しいという性質があります。例えば、1日あたりの問い合わせ件数が平均2件の場合、その分散も2となることが期待されます。ただし、実際のデータではこの仮定が成り立たないことも多く（過分散）、その場合は負の二項分布などの代替モデルの使用を検討する必要があります。

GLMのポアソン分布は、対数リンク関数を使用して説明変数と目的変数の関係をモデル化します。これにより、予測値が必ず正の値となり、カウントデータの性質と整合性のある予測が可能となります。また、複数の説明変数の影響を同時に評価でき、それぞれの変数がどの程度目的変数に影響を与えているかを定量的に把握することができます。

1. どういった時に使えるのか

GLMのポアソン分布は、イベントの発生回数や件数を分析する際に特に有用です。例えば、コールセンターでの問い合わせ件数の予測と要因分析では、オペレーターの経験年数や顧客の属性、時間帯などがどのように問い合わせ回数に影響するかを分析できます。また、eコマースサイトでの購買回数分析では、会員ステータスやキャンペーンの効果、顧客属性などが購買頻度にどう影響するかを評価できます。医療分野では、患者の入院回数や特定の症状の発生頻度などの分析に活用できます。

参考となるデータ例：

  • 顧客別の月間注文回数や問い合わせ回数
  • 従業員の月別欠勤日数や遅刻回数
  • 製品別の不具合報告件数や修理依頼回数
  • 地域別の事故発生件数や犯罪発生件数

2. ユースケース

  • コールセンター業界での使い方

    • コールセンターでは、顧客からの問い合わせ解決までに必要となる対応回数の分析に使えます。
    • オペレーターの経験年数、問い合わせ種別、緊急度などの要因が解決までの対応回数にどう影響するかを分析できます。
    • これにより、経験の浅いオペレーターへの重点的なトレーニングや、特定の問い合わせ種別への対応プロセス改善といった施策を検討できます。

  • 小売業界での使い方

    • 顧客の来店頻度や購買回数の分析に活用できます。
    • 会員ランク、年齢層、居住地域などの要因が来店頻度にどう影響するかを把握できます。
    • これにより、特定セグメントへのターゲティングや、来店促進キャンペーンの効果測定などに活用できます。

  • マーケティング担当者での使い方

    • キャンペーンやプロモーションへの反応回数の分析に使えます。
    • 顧客属性、過去の購買履歴、キャンペーン内容などが反応回数に与える影響を評価できます。
    • これにより、効果的なセグメント選定や、キャンペーン内容の最適化が可能になります。

  • 品質管理担当者での使い方

    • 製品不具合の発生回数や報告件数の分析に活用できます。
    • 製造ライン、製造時期、原材料ロットなどの要因が不具合発生回数に与える影響を特定できます。
    • これにより、品質管理プロセスの改善や、予防的なメンテナンス計画の策定が可能になります。

3. Exploratoryで一般化線形モデル - GLM - ポアソン分布を実行する

使用するデータ

今回は「コールセンターの問合せデータ」を使用します。データはこちらからダウンロードが可能となっています。

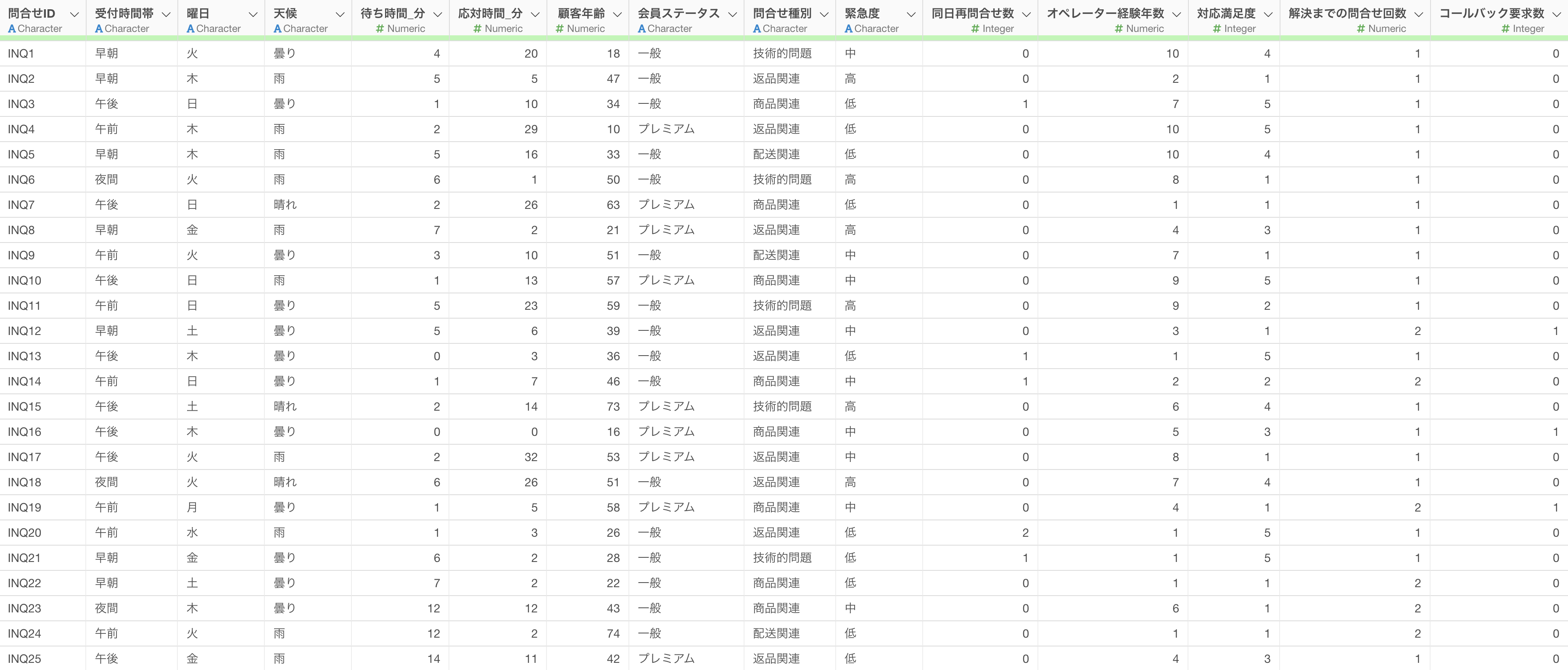
このデータは各問い合わせ案件が1行を構成し、列には「オペレーター経験年数」「待ち時間_分」「緊急度」「対応満足度」といったデータがあります。

GLM - ポアソン分布を作るためには、以下のようなデータの構造が必要となります。

  • 目的変数は0以上の整数値であること（カウントデータ）
  • 予測変数は数値型またはカテゴリ型であること
  • 極端な外れ値が含まれていないこと

アナリティクスを作成する

コールセンターの問合せデータから「アナリティクス・ビュー」を開きます。

タイプに「一般化線形モデル」を選び、「GLM - ポアソン分布」を選択します。

目的変数には「解決までの問合せ回数」の列を割り当てます。

予測変数には、「受付時間帯」から「コールバック要求数」の列を選択して割り当てます。

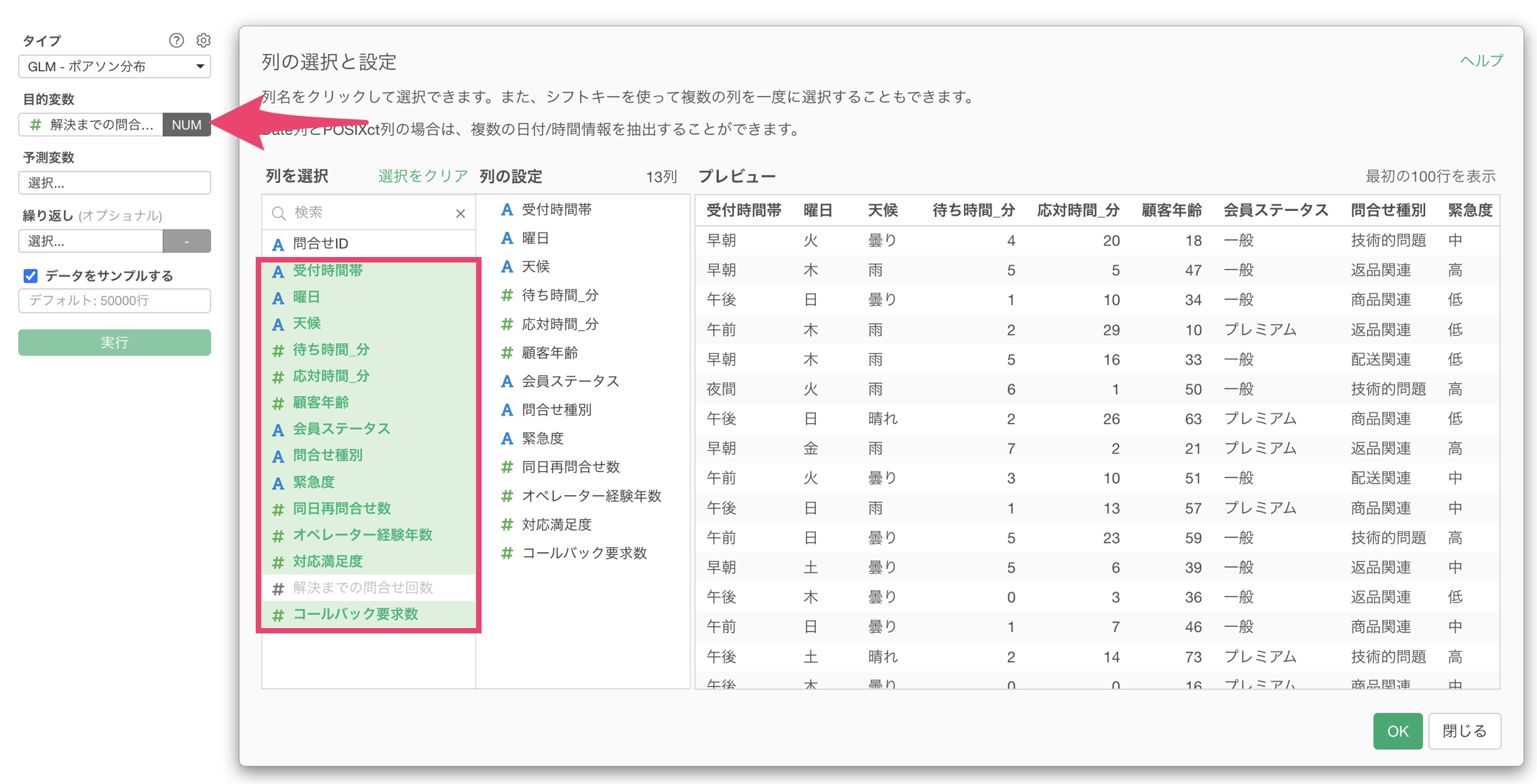
最後に、「実行」ボタンをクリックして実行結果を確認します。

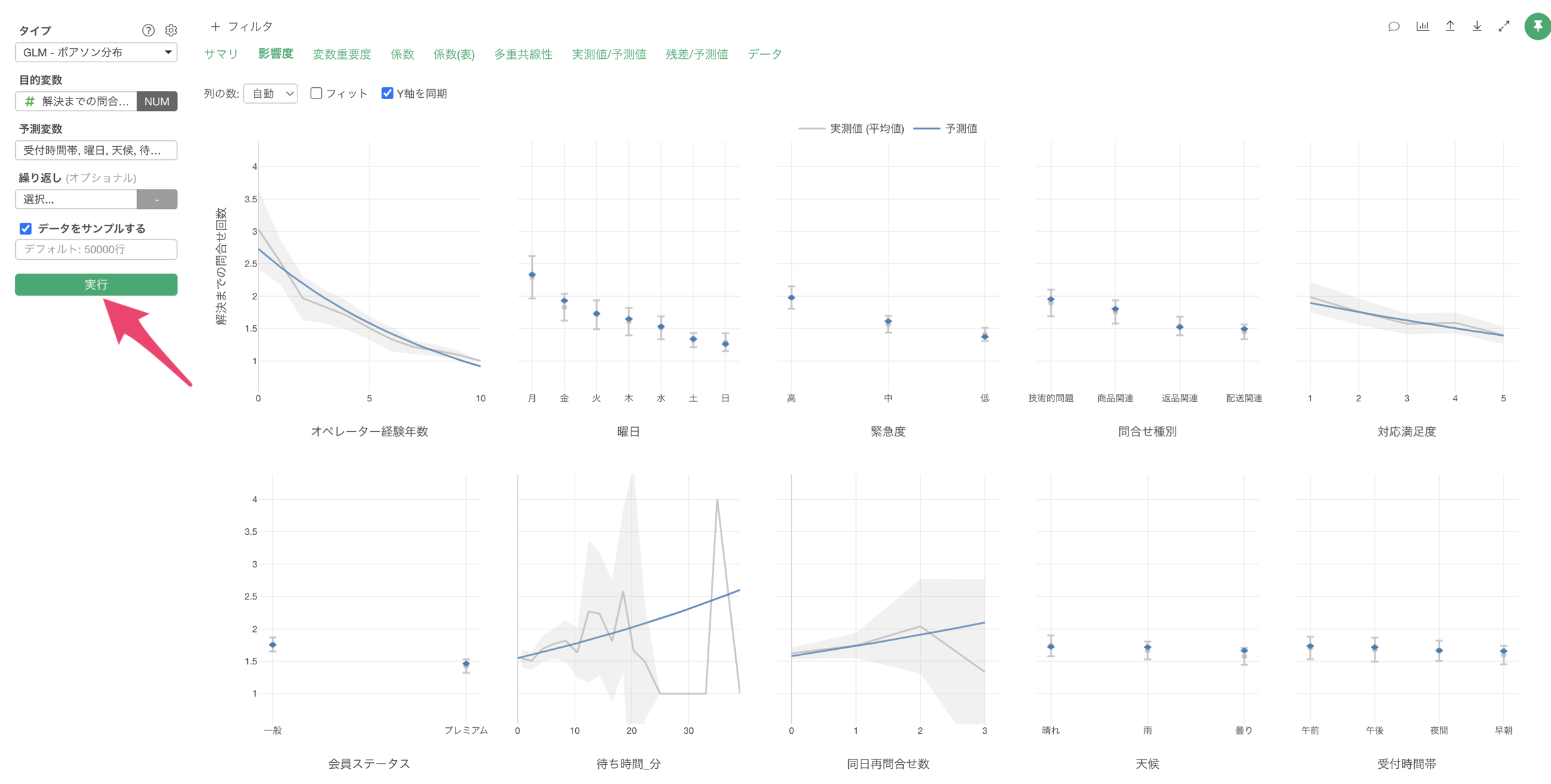
結果の解釈

GLM - ポアソン分布では、解決までの問合せ回数を予測するために各変数の影響度を解釈するために以下のタブがあります。

多重共線性

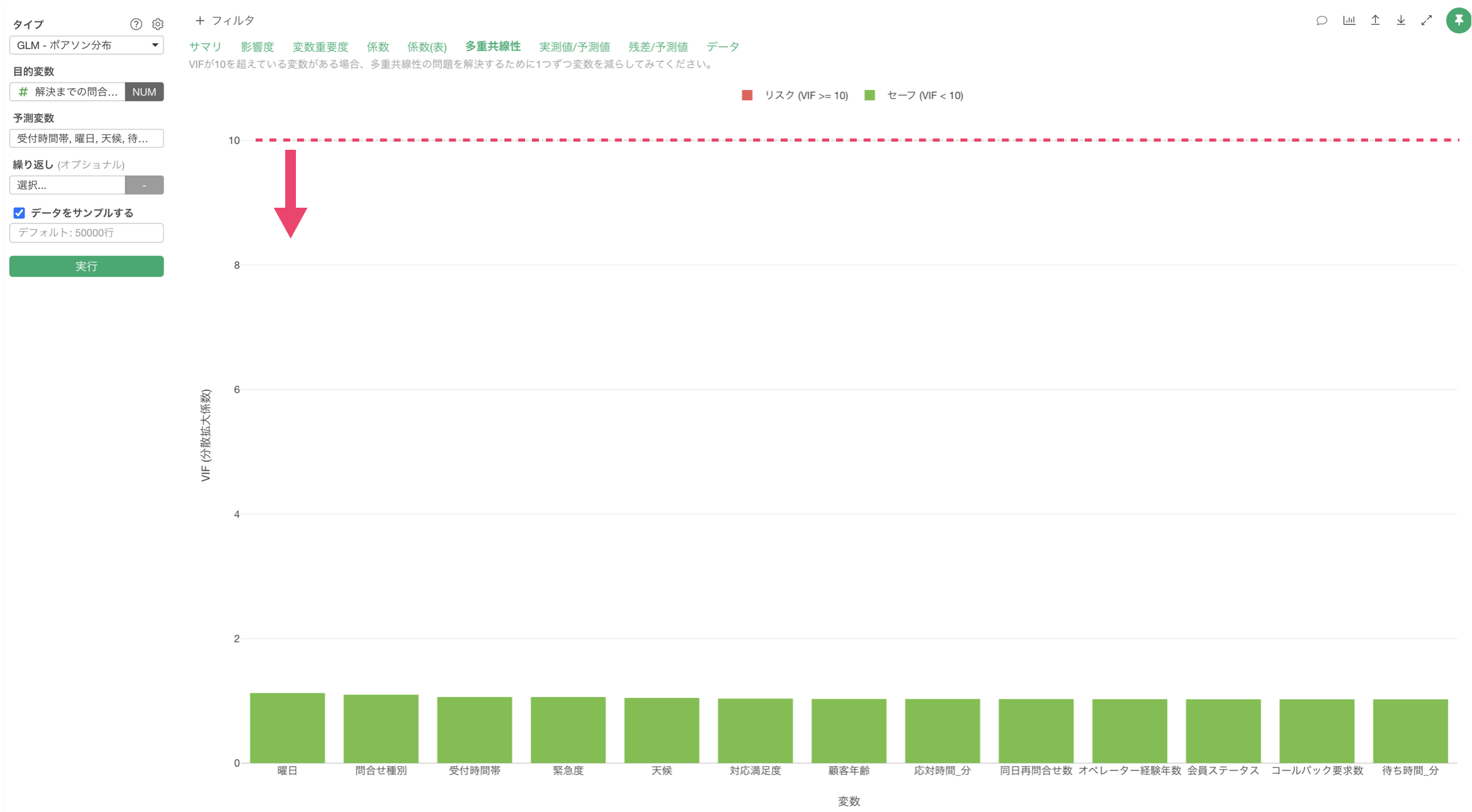
「多重共線性」タブをクリックすると、予測変数間の相関が強すぎる（VIF > 10）組み合わせがないかを確認できます。VIFが10以上の変数がある場合、モデルの信頼性に影響を与える（傾きが不安定になる）可能性があるため、変数の選択を見直す必要があります。

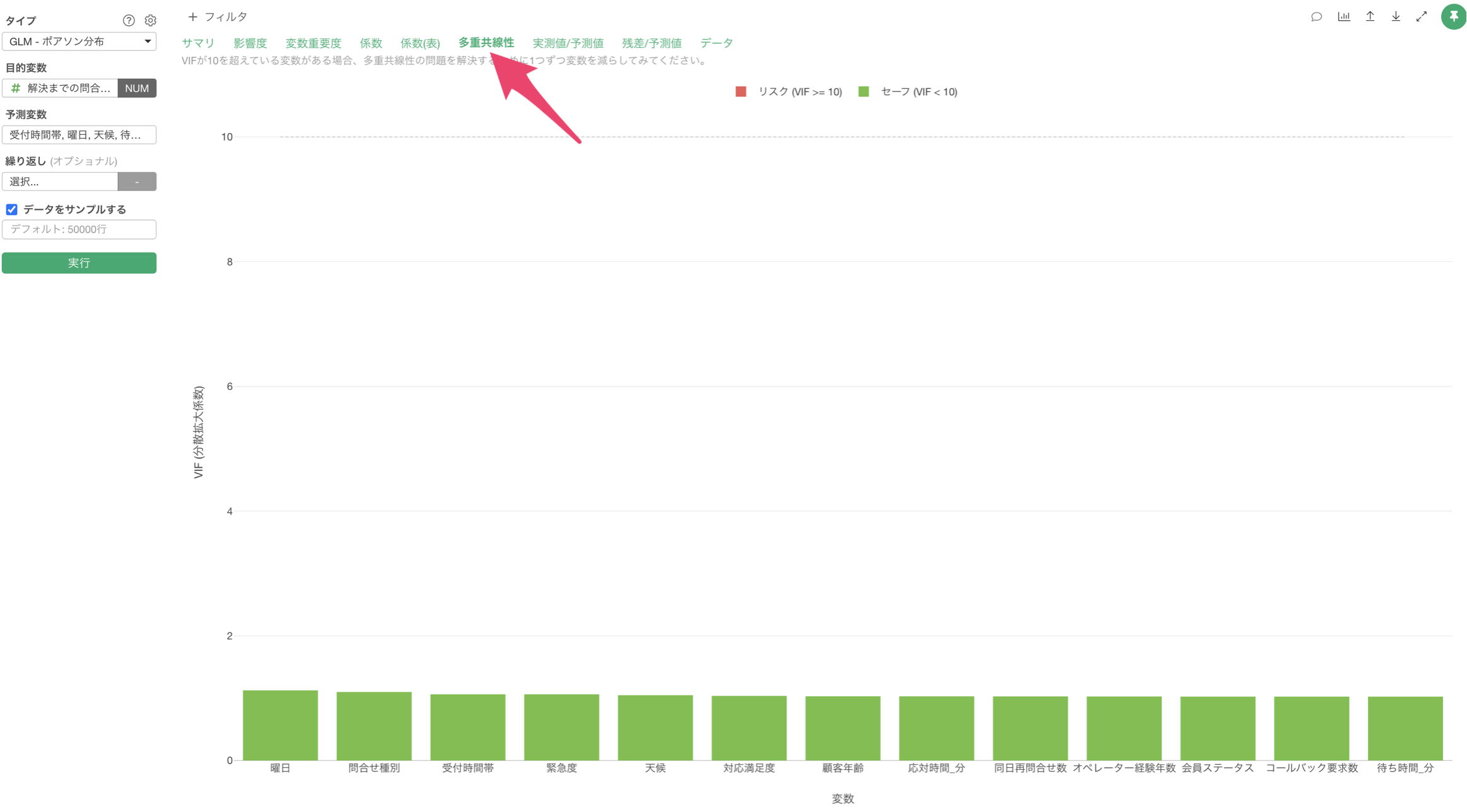
今回の結果は、VIFが10以上のものはないため、予測変数同士に相関が強すぎる変数の組み合わせがないため、モデルが不安定であることはないことがわかります。

変数重要度

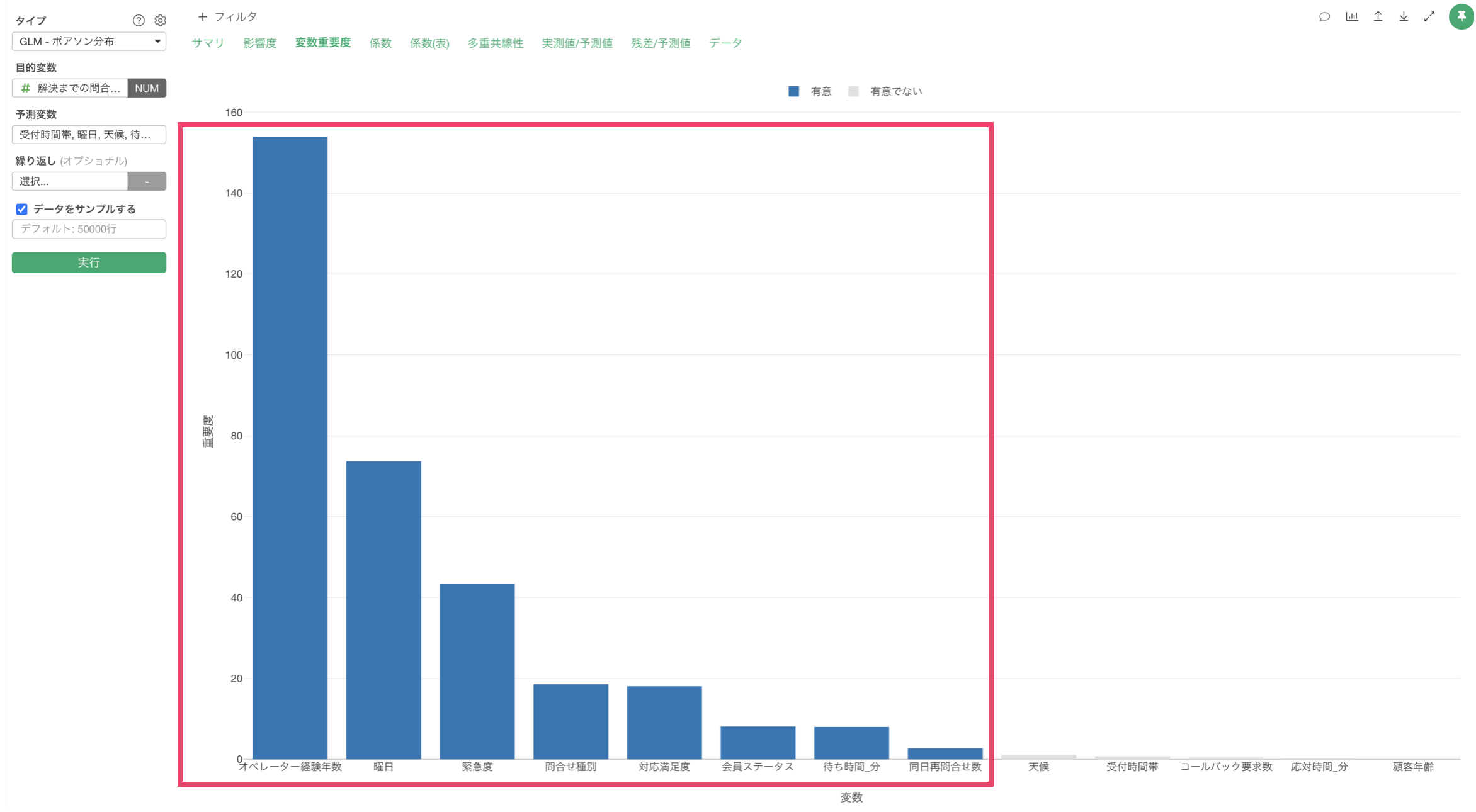
「変数重要度」タブをクリックすると、目的変数を予測する上でどの変数が重要なのかを確認することができます。

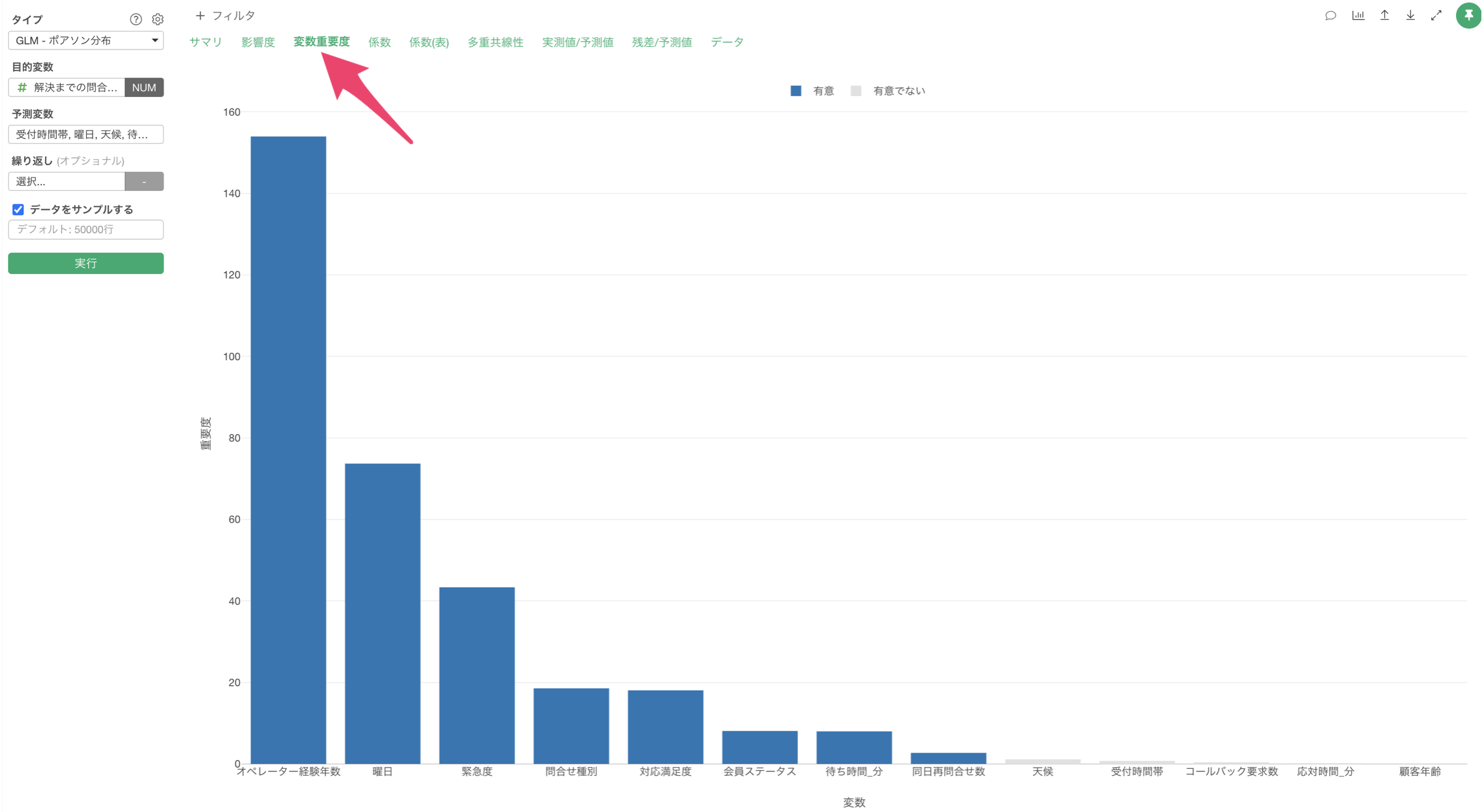
この結果から、解決までの問い合わせ回数の予測に最も重要な変数はオペレーター経験年数であり、次いで曜日、緊急度の順となっていることがわかります。

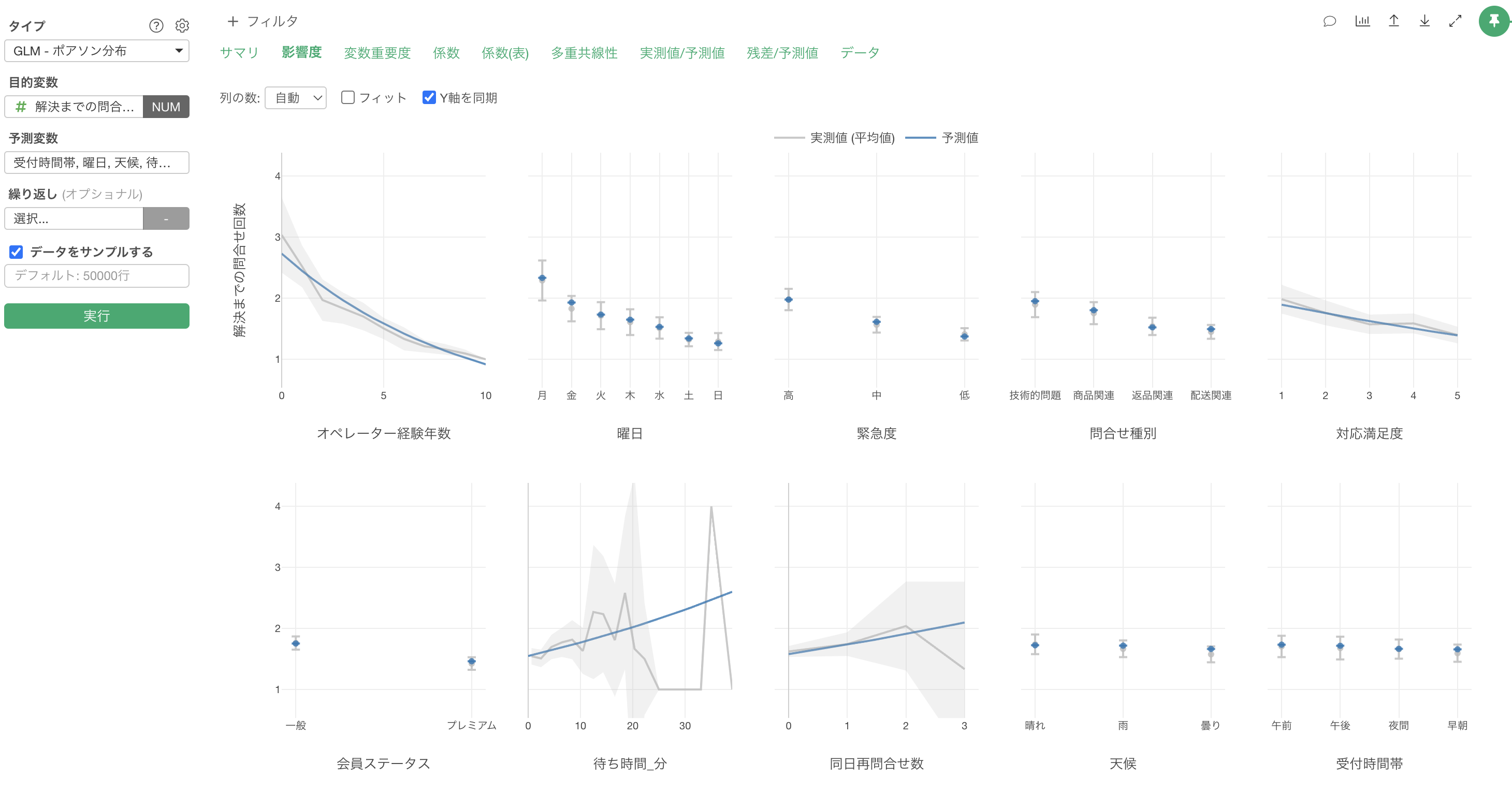
影響度

「影響度」タブでは、各予測変数が製造時間に与える影響の方向と強さを確認することができます。

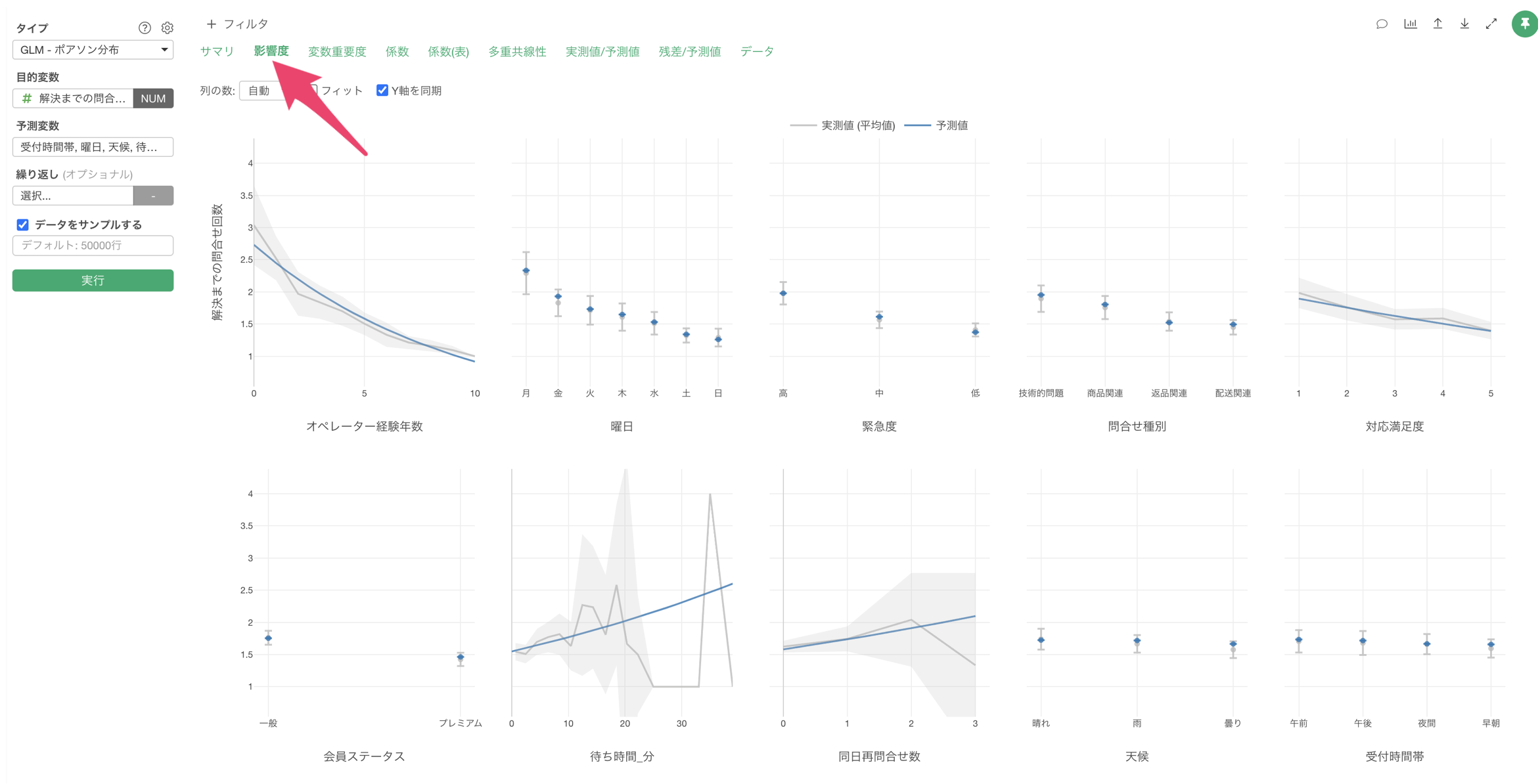
例えば、オペレーター経験年数が上がると、解決までの問い合わせ回数も減ることが確認出来ます。

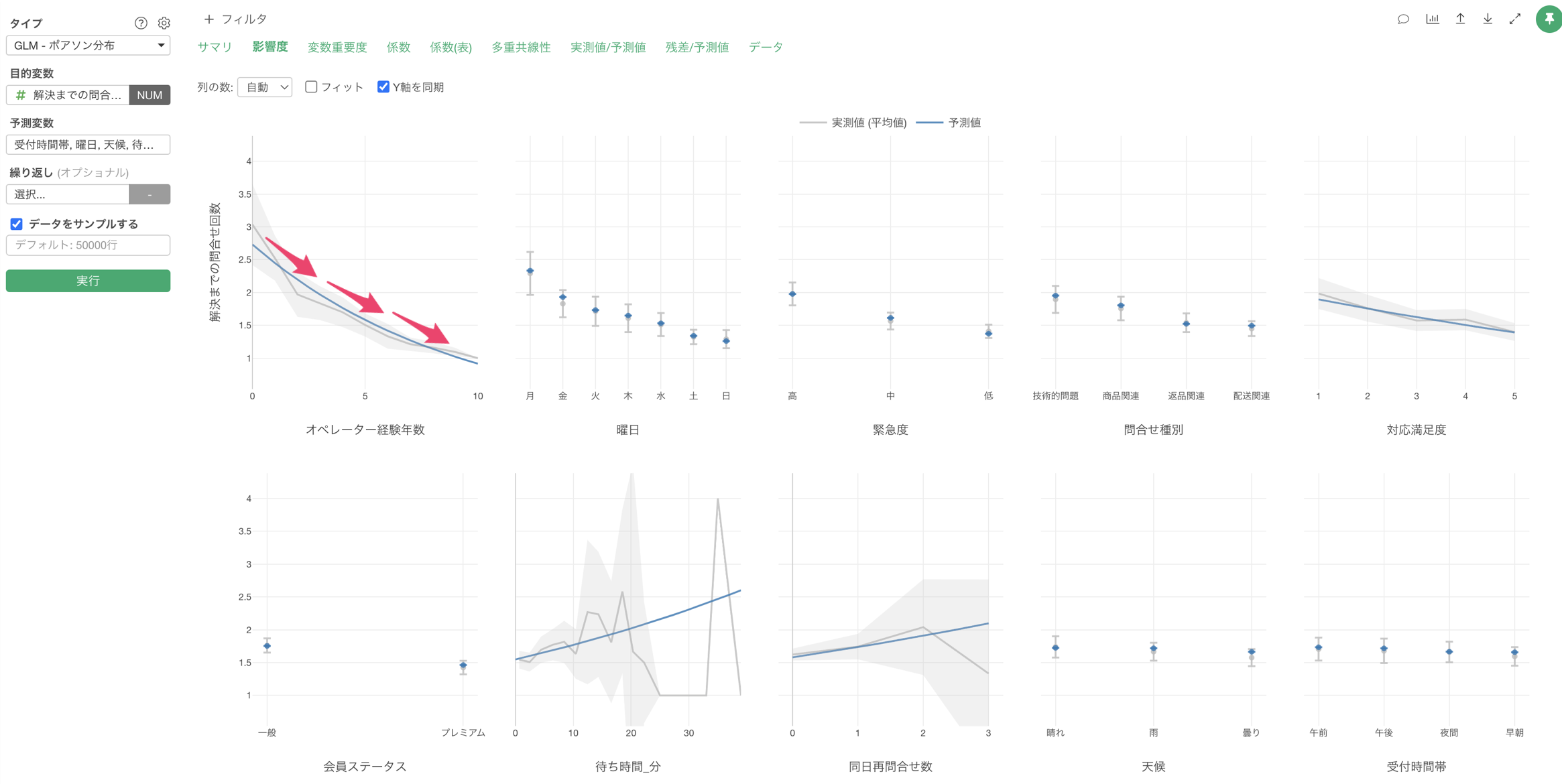
また、曜日が月曜日の場合は、他に比べて解決までの問い合わせ回数が多いことがわかります。

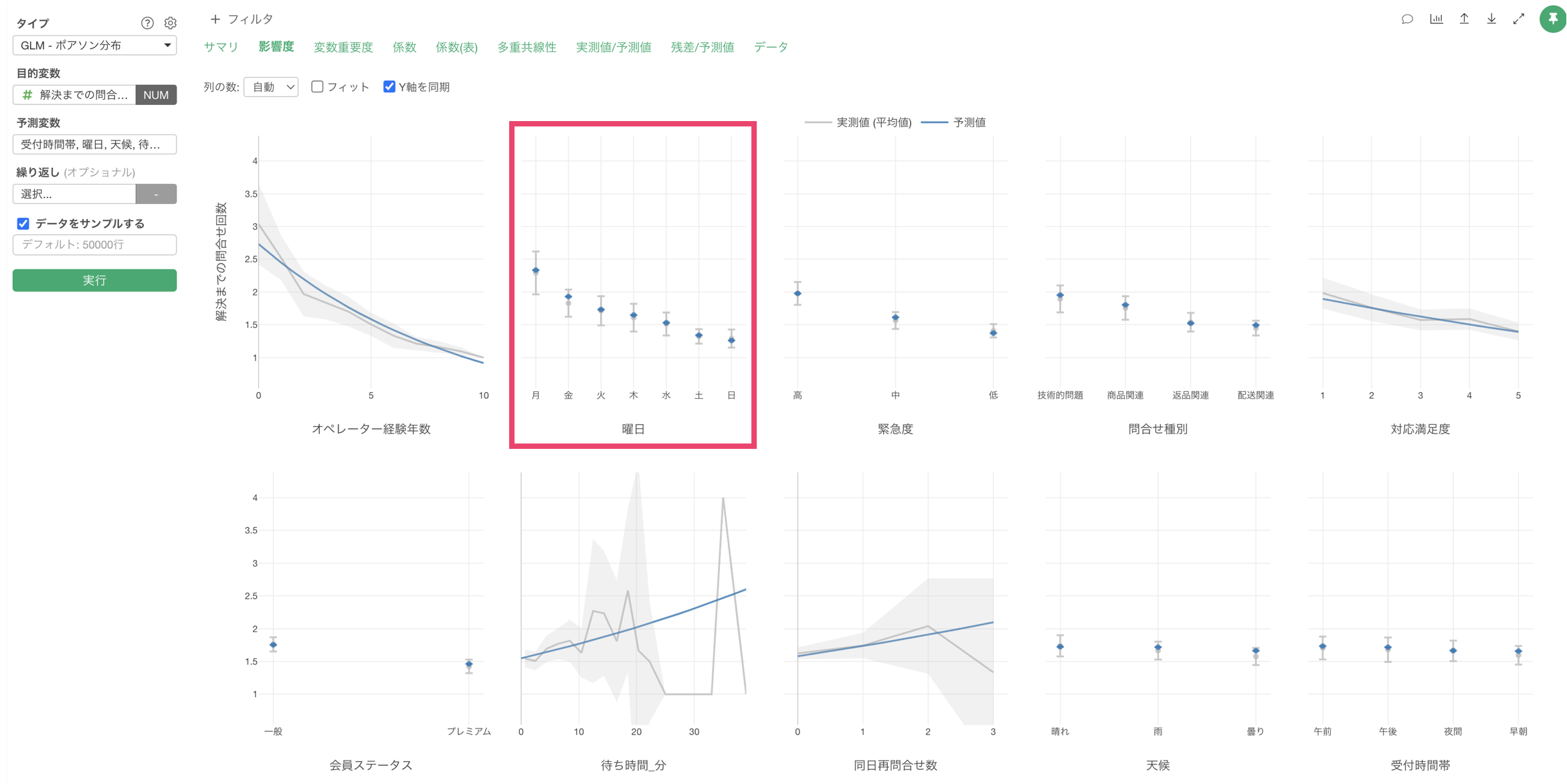
係数

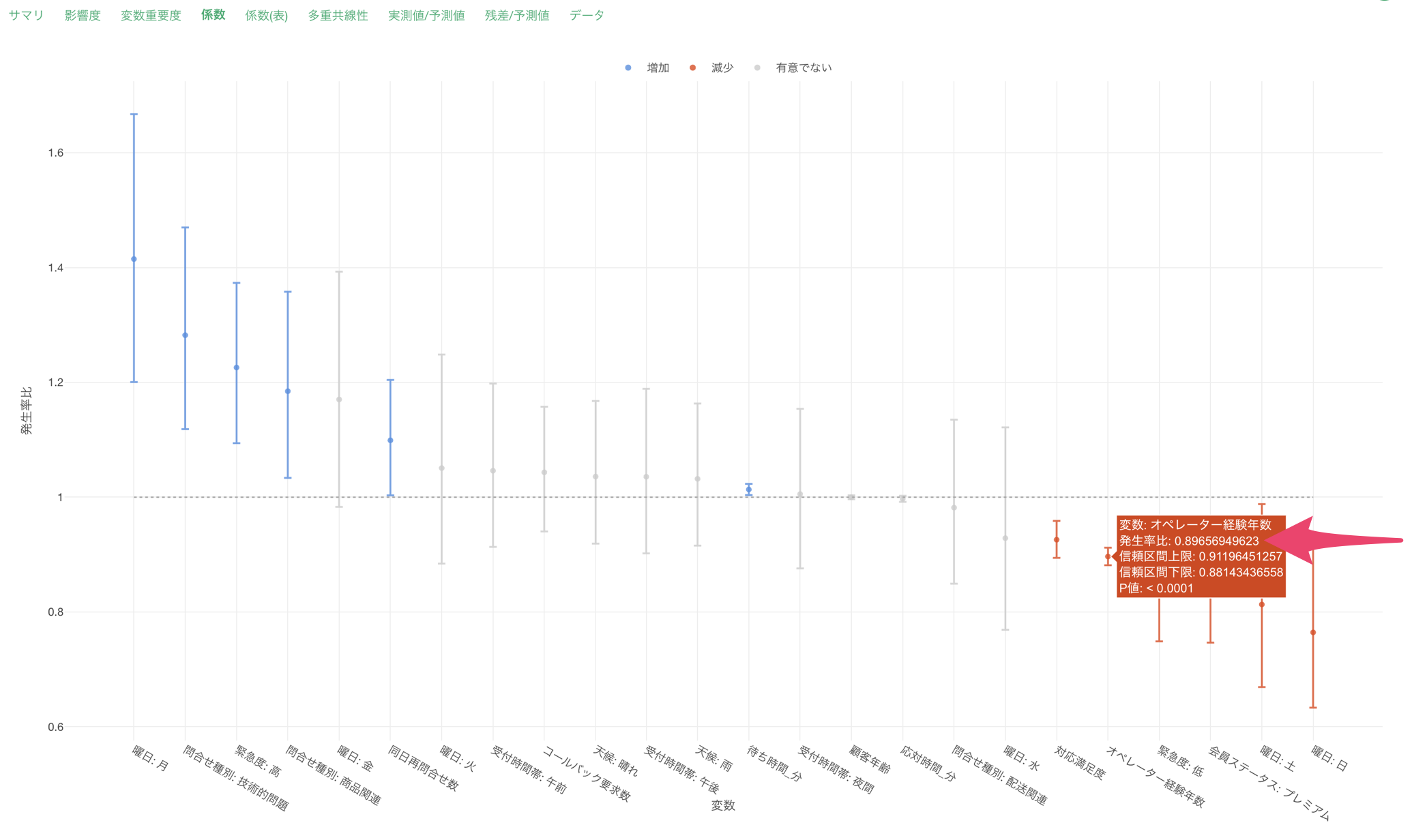
「係数」タブでは、各予測変数の係数とその統計的有意性を確認することができます。

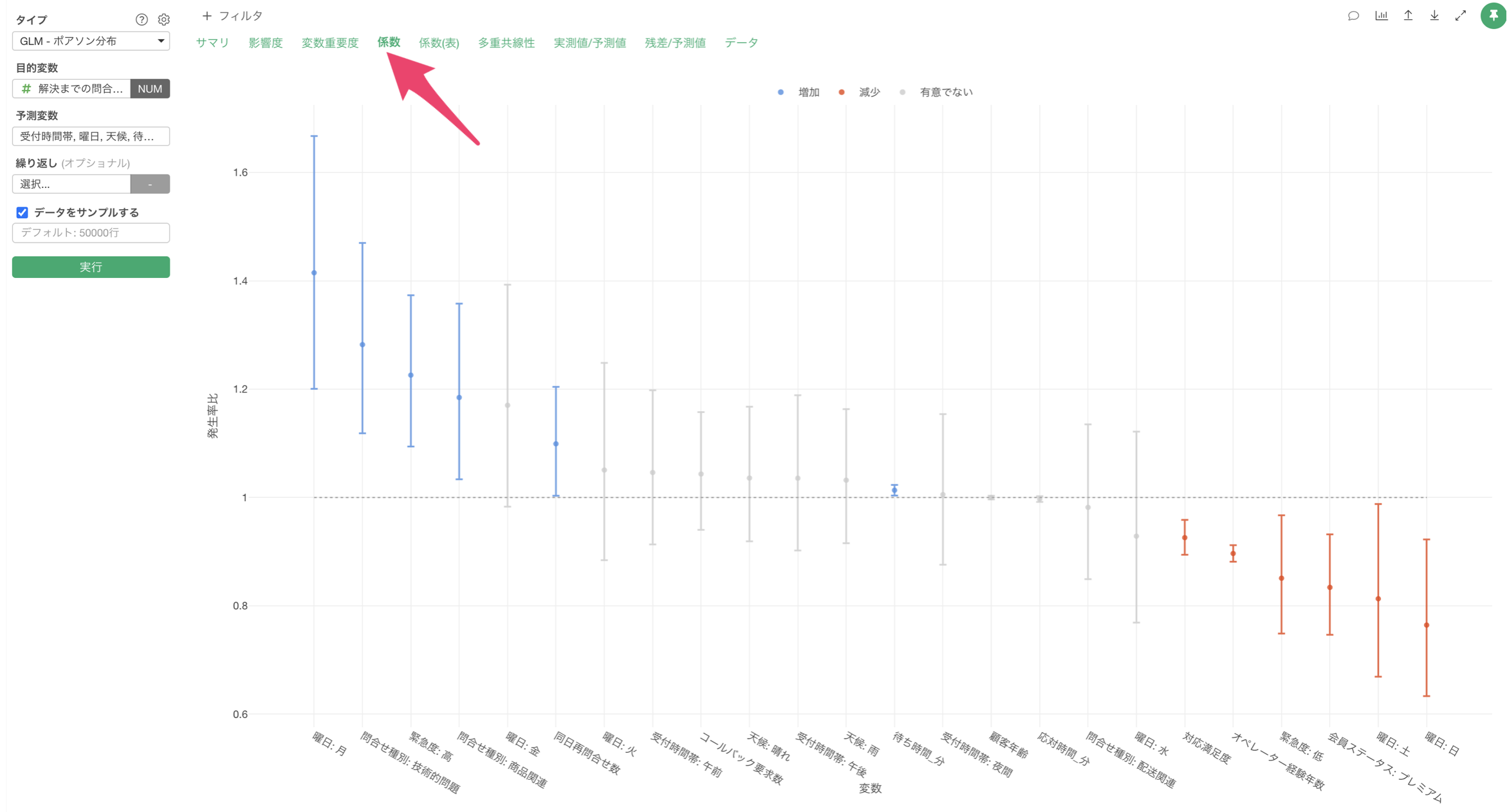
この結果から、各変数の効果の大きさを数値で確認できます。また、P値が0.05未満の変数は、統計的に有意な影響を持っていると判断できます。

例えば、曜日がベースレベルである木曜日から月曜日になると、発生率比が1.414のため解決までの問い合わせ回数が1.414倍になる傾向があると解釈が出来ます。P値も0.0001未満のため、統計的に有意な関係があると判断が出来ます。

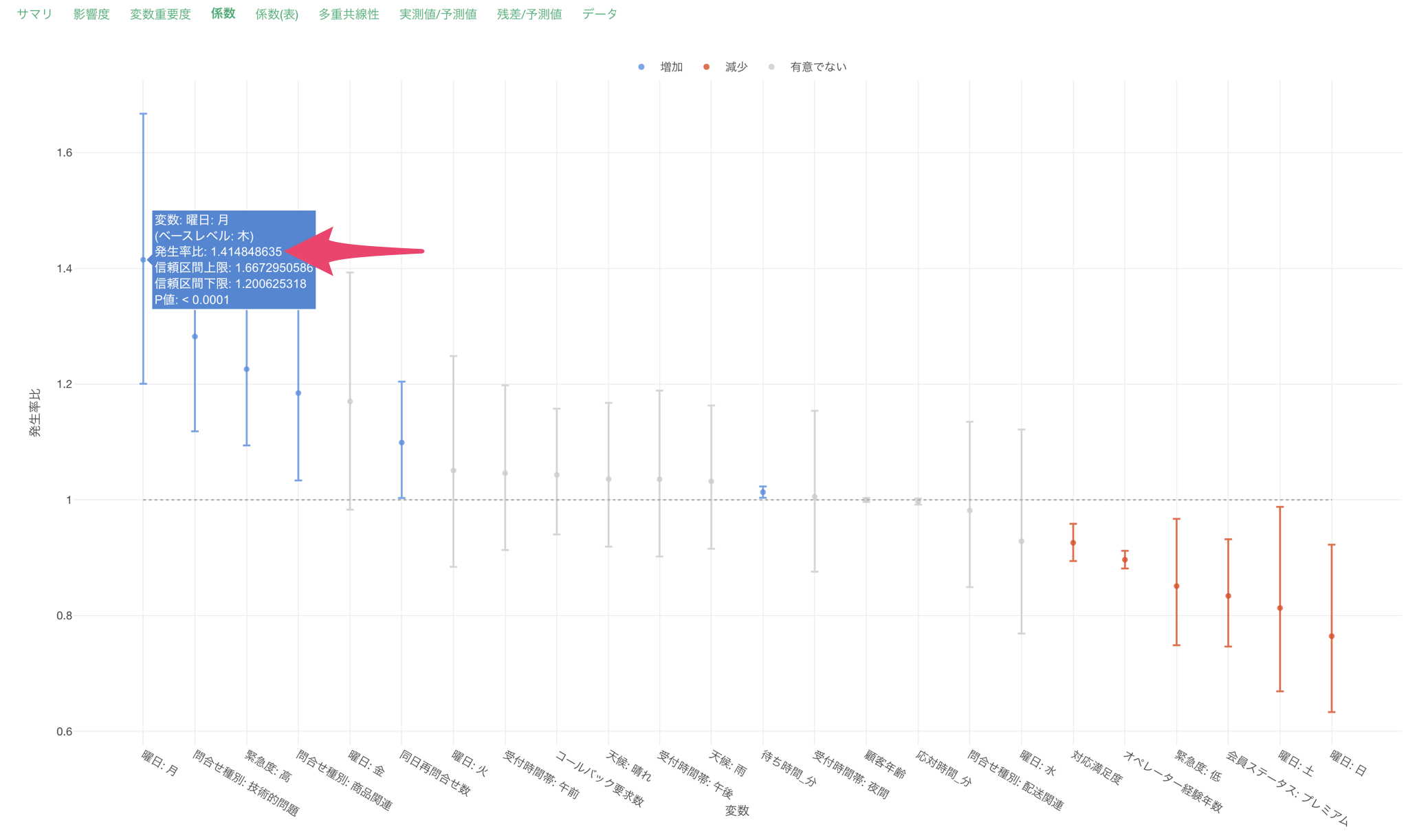
オペレーターの経験年数の発生率比0.897は、経験年数が1年増えるごとに問い合わせ回数が約10.3%（1 - 0.897 = 0.103）減少することを意味します。P値も0.0001未満のため、統計的に有意な関係があると判断が出来ます。

サマリ

「サマリ」タブをクリックすると、モデル全体の予測精度を確認することができます。

逸脱度の減少率

モデルがデータをどれだけ上手く説明できているかを示す指標です。値が大きいほど、モデルの説明力が高いことを意味します。

逸脱度減少率=Nullモデルの逸脱度−残差逸脱度Nullモデルの逸脱度×100 = 100逸脱度減少率=Nullモデルの逸脱度Nullモデルの逸脱度−残差逸脱度×100

基準値：

  • 20%以上：とても良い
  • 10-20%：十分な改善
  • 5-10%：ある程度の改善
  • 5%未満：改善が小さい

今回の場合は以下のように計算ができ、45.68%の減少は、予測変数を加えることでモデルの説明力が大きく向上したことを示しています。

((730.455374754066 - 396.731317175746) / 730.455374754066) * 100 = 45.68%

4. まとめ

GLM - ポアソン分布は、コールセンターの問い合わせ回数のような離散的なカウントデータの分析に適した手法です。今回の分析では、オペレーター経験年数や曜日、緊急度などが問い合わせ回数に有意な影響を与えていることが明らかになりました。これらの知見は、オペレーターの配置最適化や、曜日別の対応体制の調整など、具体的な業務改善施策の立案に活用できます。

参考資料

  • アナリティクス・ギャラリー - リンク
Export Chart Image
Output Format
PNG SVG
Background
Set background transparent
Size
Width (Pixel)
Height (Pixel)
Pixel Ratio