統計的検定における多重性について
統計分析において多重性(Multiple Comparisons)は、複数の統計的検定を同時に行う際に生じる問題です。例えば、ECサイトで複数の商品カテゴリー間で売上の差を比較する場合などに、私たちは複数の検定を同時に実施することになります。このような状況で多重性を考慮せずに分析を行うと、第一種の過誤(偽陽性)が増加してしまう危険性があります。
具体的には、統計的有意水準を5%(p < 0.05)に設定した場合、1回の検定では5%の確率で誤って帰無仮説を棄却してしまう可能性があります。しかし、同じデータに対して複数回の検定を行うと、少なくとも1回は誤って有意差があると判断してしまう確率が増加します。例えば、独立した10回の検定を行う場合、少なくとも1回は誤って有意差があると判断してしまう確率は40%以上に達します。
基本的な考え方
- 個々の検定での正しい判断の確率は95%(1 - 0.05)
- 誤った判断(第1種の過誤)の確率は5%(0.05)
複数回の検定での確率計算
- 全ての検定で正しい判断をする確率:0.95^10 = 0.5987(約59.87%)
- したがって、少なくとも1回は誤判断する確率:1 - 0.5987 = 0.4013(約40.13%)
検定回数による誤った判断の可能性
- 1回の検定:5.00%
- 5回の検定:22.62%
- 10回の検定:40.13%
- 20回の検定:64.15%
このような問題に対処するため、多重性を考慮した分析手法が開発されてきました。代表的なものとしては、Bonferroni法、Holm法、Tukey法などがあります。これらの手法を適切に使用することで、複数の比較を行う際でも第一種の過誤を適切な水準にコントロールすることが可能となります。特に、ビジネスの意思決定に統計的な分析結果を活用する場合、誤った判断によるリスクを最小限に抑えるために、多重性の考慮は不可欠な要素となっています。
多重比較の代表的な手法
Bonferroni法
最も単純で保守的な多重比較の手法です。個々の検定の有意水準をα/n(nは検定の総数)に設定することで、全体の有意水準をαに保ちます。
メリット:
- 計算が簡単で理解しやすい
- どのような検定にも適用可能
デメリット:
- 検定力が低い(差があっても検出できない可能性が高い)
- 検定回数が多いと極端に保守的になる
Holm法(ステップダウン法)
Bonferroni法を改良した手法です。具体的には、まず全てのp値を小さい順に並べ、最も小さいp値から順番に判断していきます。最初のp値は「有意水準÷検定の総数」と比較し、2番目のp値は「有意水準÷(検定の総数-1)」と比較するというように、分母を1つずつ減らしながら判断を進めていきます。この過程で、一度でも「有意でない」と判定されたら、そこで判定を終了し、残りのp値はすべて「有意でない」と判断します。
メリット:
- Bonferroni法より検定力が高い
- 計算が比較的簡単
デメリット:
- 検定回数が多い場合は依然として保守的
Tukey HSD法(Honestly Significant Difference)
Tukey法の一種で、全てのペアワイズ比較に対して一つの臨界値を使用する方法です。このTukey HSD法は、特にANOVA後の多重比較において最もよく使用される手法の一つで、検定力と制御のバランスが取れているため、実務でも広く採用されています。ExploratoryでのANOVA検定でもデフォルトで設定しているのがTukey HSD法となります。
メリット:
- すべての可能なペアの比較を一度に実行可能
- 各比較の信頼区間を提供
デメリット:
- グループのサンプルサイズが等しいことを仮定
- 正規性と等分散性の仮定が必要
Exploratoryで多重性を考慮して検定を行う方法
One-way ANOVA
One-way ANOVAは、1つのカテゴリ型の変数(説明変数)が数値変数(目的変数)に与える影響を分析する手法です。
例えば、以下は営業担当別の売り上げデータとなりますが、経験年数区分によって売上金額に違いがあるのかを検定したいとします。
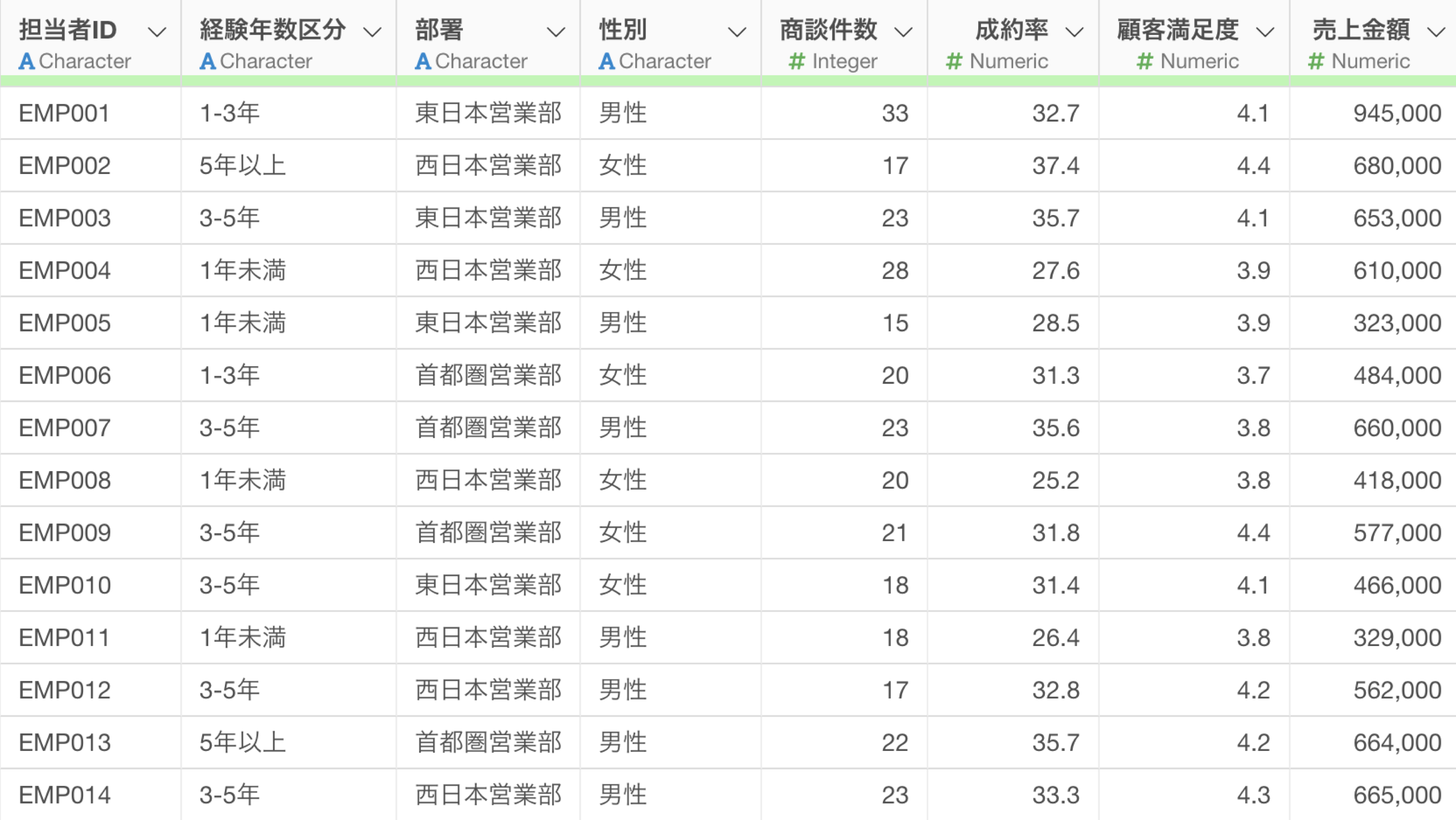
その場合は、One-Way ANOVAを使用することで、経験年数区分による売上金額に有意差があるかどうかを検定できます。
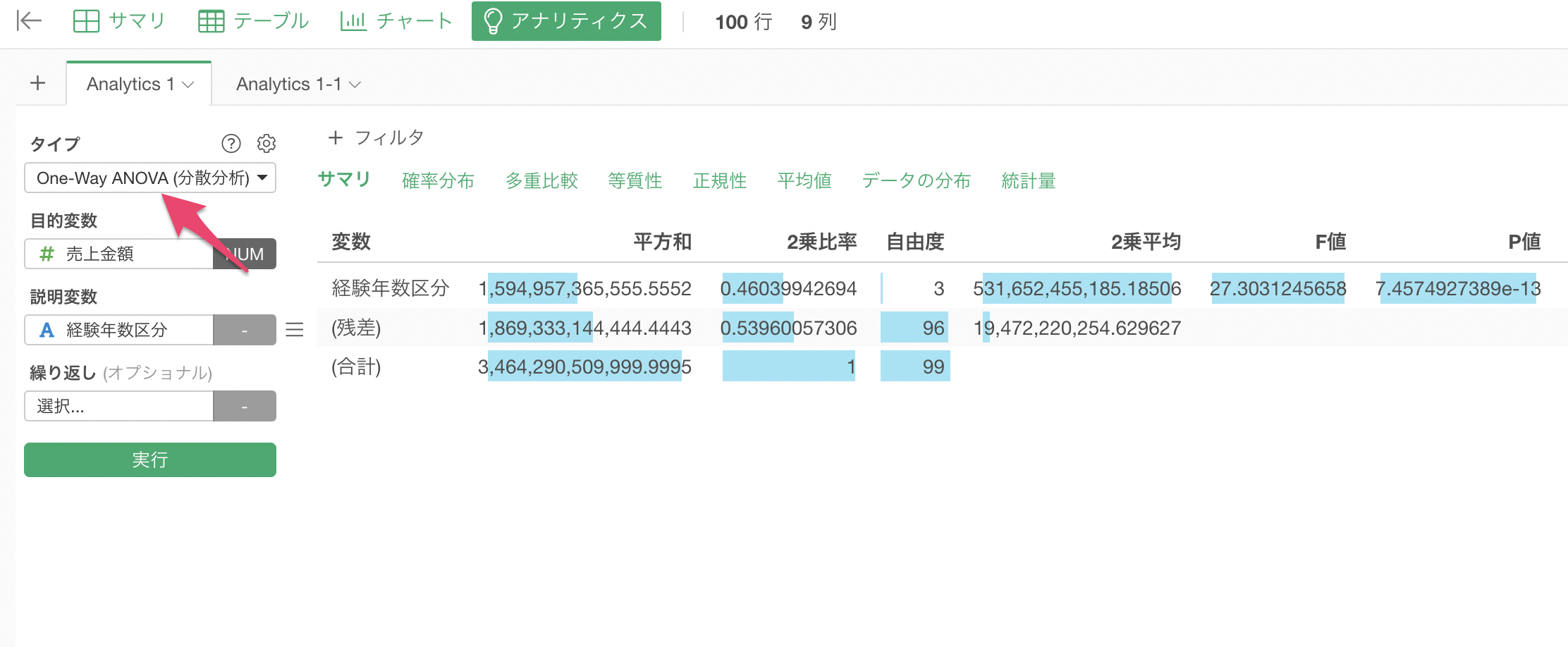
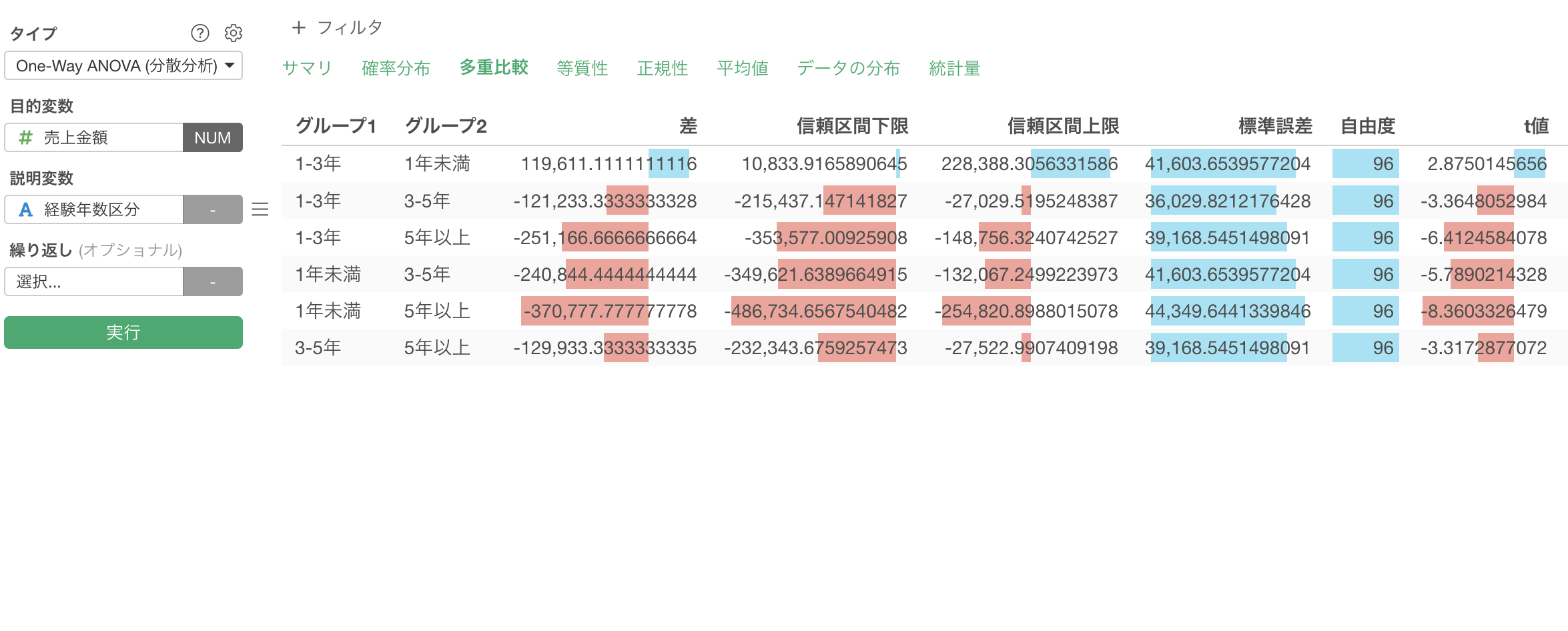
One-Way ANOVAでは、多重比較のタブが用意されているため、多重性を考慮した上でそれぞれの組み合わせで有意かどうかを確認できます。
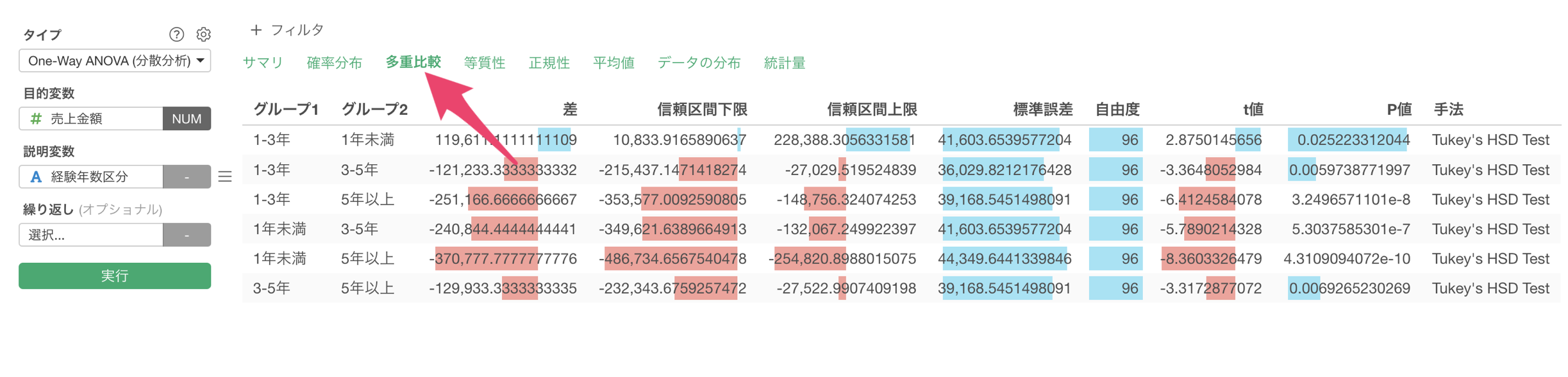
One-way ANOVAの詳しい使い方については、こちらのノートをご覧ください。
Two-way ANOVA
Two-way ANOVAは、2つのカテゴリ型の変数(説明変数)が数値変数(目的変数)に与える影響を分析する手法です。
例えば、以下は小売業の顧客購買のデータとなりますが、年齢層と性別によって購入金額に違いがあるのかを検定したいとします。
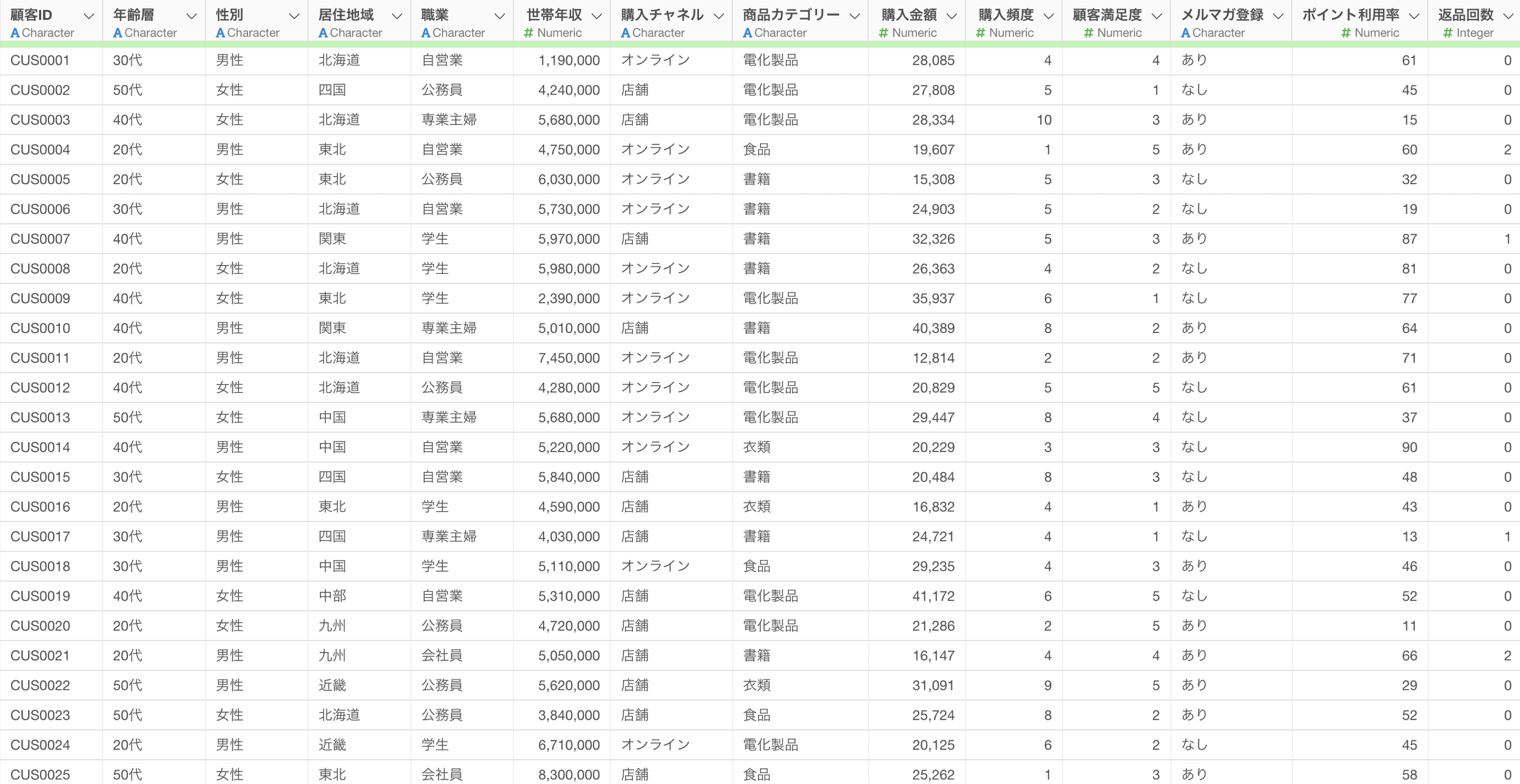
その場合は、Two-Way ANOVAを使用することで、年齢層と性別による購入金額に有意差があるかどうかを検定できます。
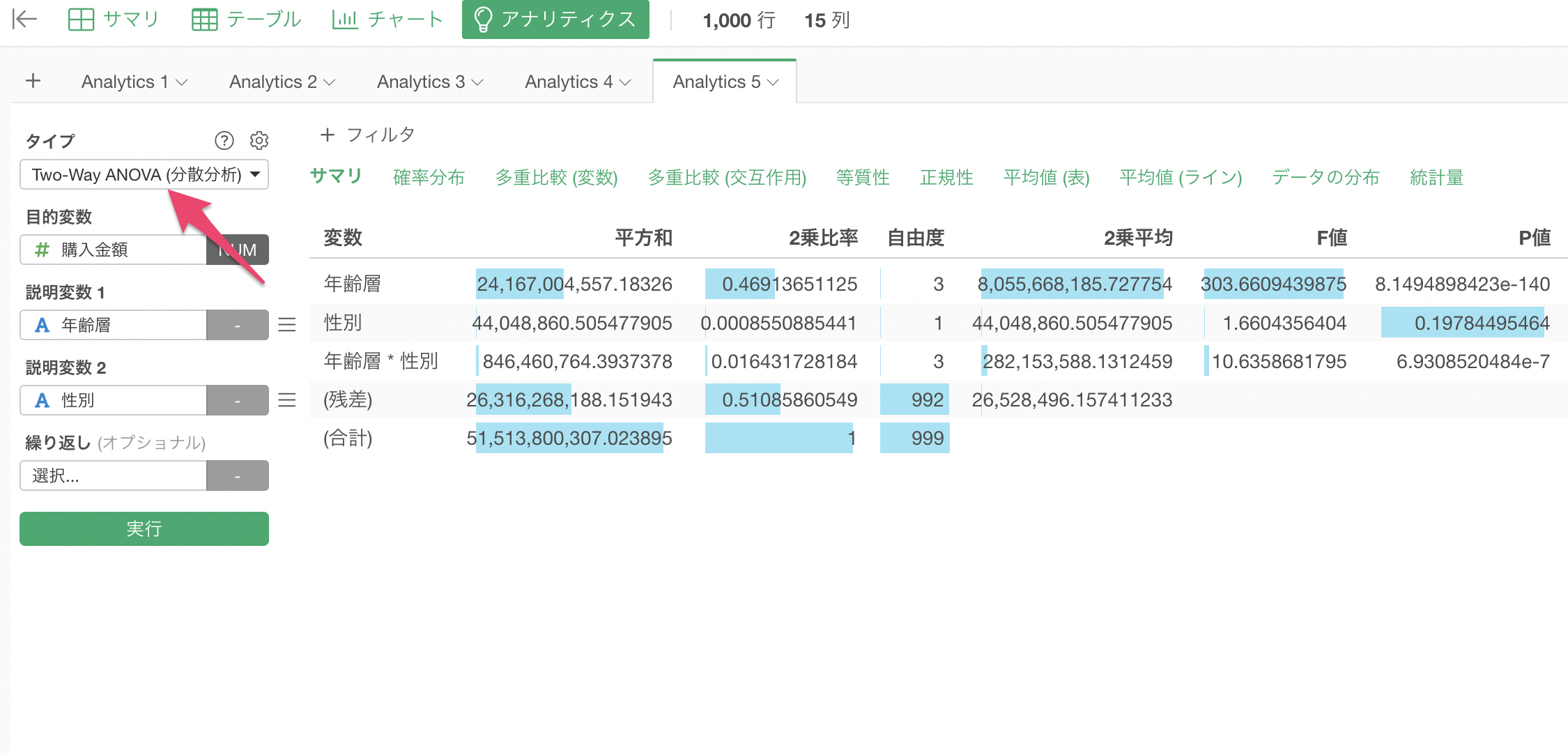
「多重比較 (変数)」をクリックすると、各年齢層間、性別間での購入金額の差の統計的有意性を確認することができます。

「多重比較 (交互作用)」をクリックすると、年齢層と性別の組み合わせによる購入金額の差の統計的有意性を確認することができます。
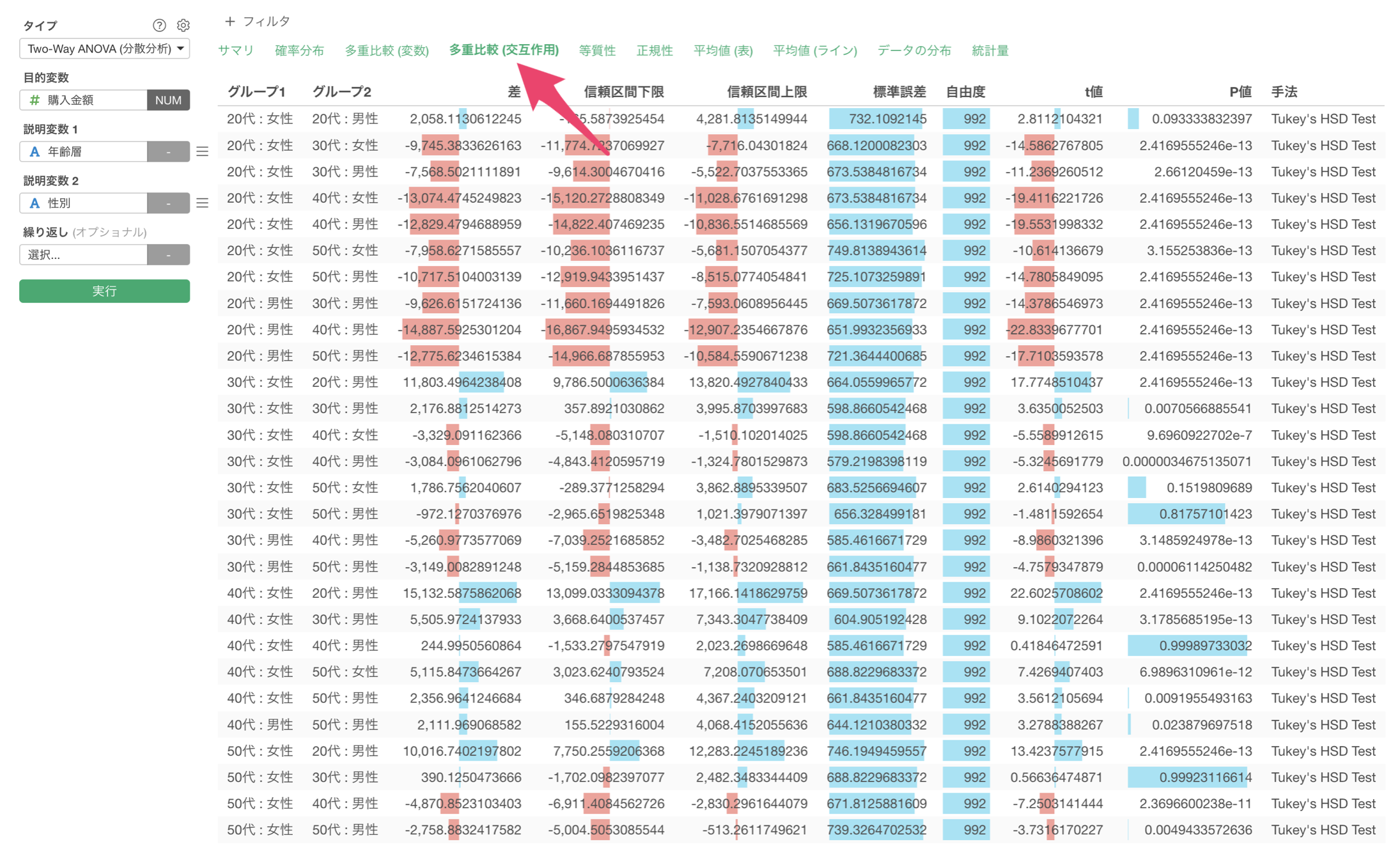
Two-way ANOVAの詳しい使い方については、こちらのノートをご覧ください。
まとめ
統計的検定における多重性は、同一データに対して複数の検定を行う際に生じる重要な問題です。例えば、有意水準5%で10回の独立した検定を行う場合、少なくとも1回は誤って有意差があると判断してしまう確率が約40%に達するなど、検定回数の増加に伴って誤判断のリスクが高まります。
Exploratoryでは、One-way ANOVAやTwo-way ANOVAなどの分析手法において、これらの多重比較の手法を実装しており、Tukey HSD法がデフォルトで設定されています。これにより、カテゴリ変数が目的変数に与える影響を分析する際に、多重性を適切に考慮した検定を簡単に実行することができるようになっています。