ロジスティック回帰の使い方
ロジスティック回帰の使い方や結果の解釈の仕方、よくある質問をご紹介します。
ロジスティック回帰は線形回帰と似ていますが、線形回帰は目的変数が「数値」を対象としているのに対し、ロジスティック回帰では目的変数が「二値」のロジカル型を対象としています。例えば、この人はコンバージョンするのかどうか、離職するのかどうかといった「はい」、「いいえ」で決まるようなデータです。このロジスティック回帰のシンプルさと説明力の高さゆえに、現在でもデータサイエンスの世界では最もよく使われる統計学習(または機械学習)アルゴリズムの一つです。
ロジスティック回帰を使うことで、下記の質問に答えていくことができます。
- このデータ(予測変数)を使うことで目的変数(例:コンバージョン)のTRUE/FALSEをどれだけ上手く分けられているのか。
- どの変数が目的変数を予測する上で重要なのか。
- 変数の値が変わると、目的変数の値はどのように変わるのか。
- その予測変数は、目的変数の変化を説明するうえで有意と言えるのか。
- 他の変数が一定とした時に、変数の値が1上がると目的変数の値はどれだけ上がるのか、または下がるのか。
必要なデータ
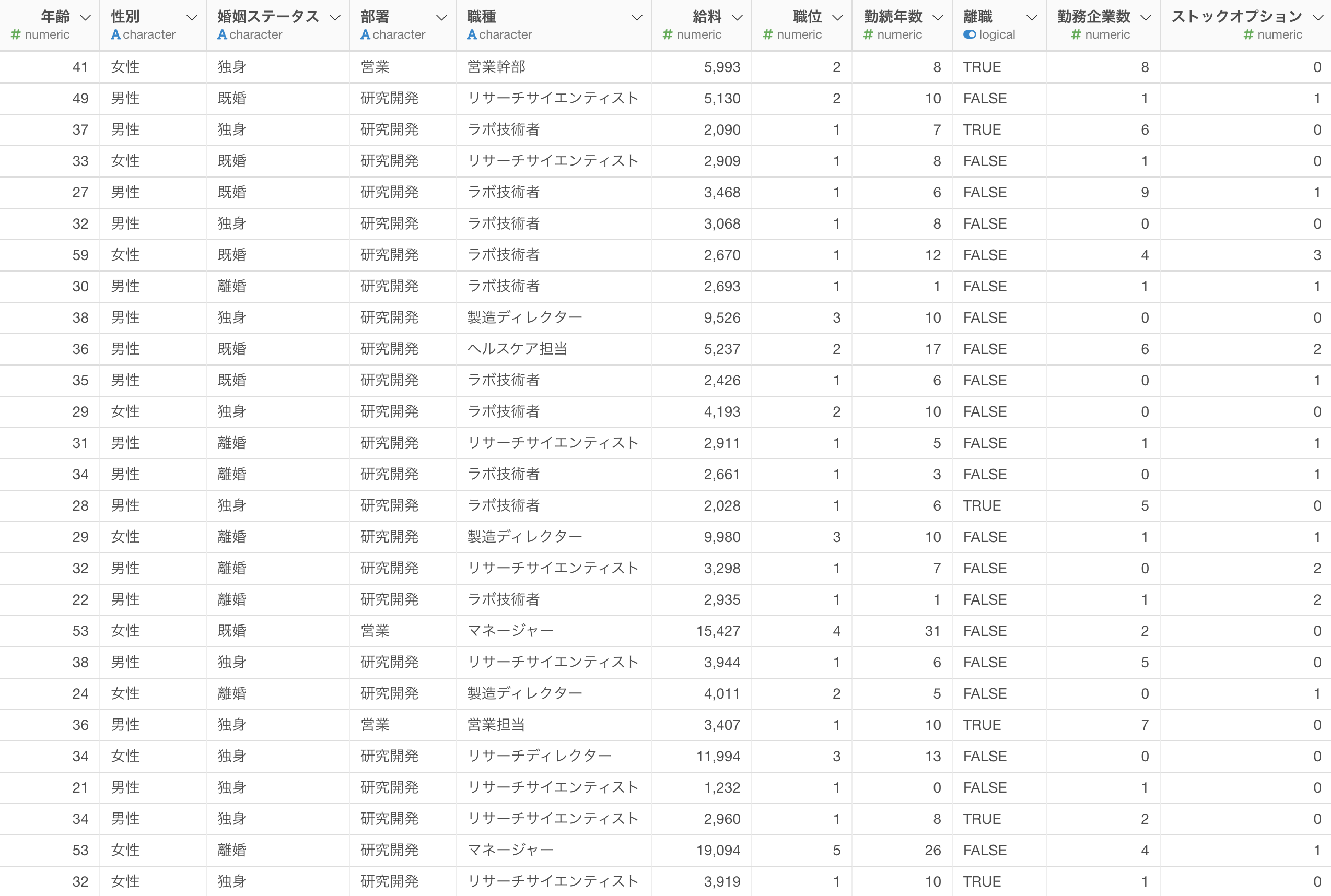
ロジスティック回帰を作成するためには、1行が1観察対象(例:1行が1従業員)となっているデータが必要です。
また、目的変数として使用できるデータタイプはTRUE/FALSEの二値をとる「ロジカル型」の列で、予測変数におけるデータタイプには特に縛りはありません。しかし、ロジスティック回帰などの統計系のモデル作成時には、予測変数どうしの相関があまりにも強い時に発生する「多重共線性」などの問題を考慮する必要があります。
もし、目的変数にしたい列のデータタイプがロジカル型になっていない場合、こちらのノートを参考にロジカル型に変更してからロジスティック回帰のモデルを作成ください。
ロジスティック回帰のモデルを作成する
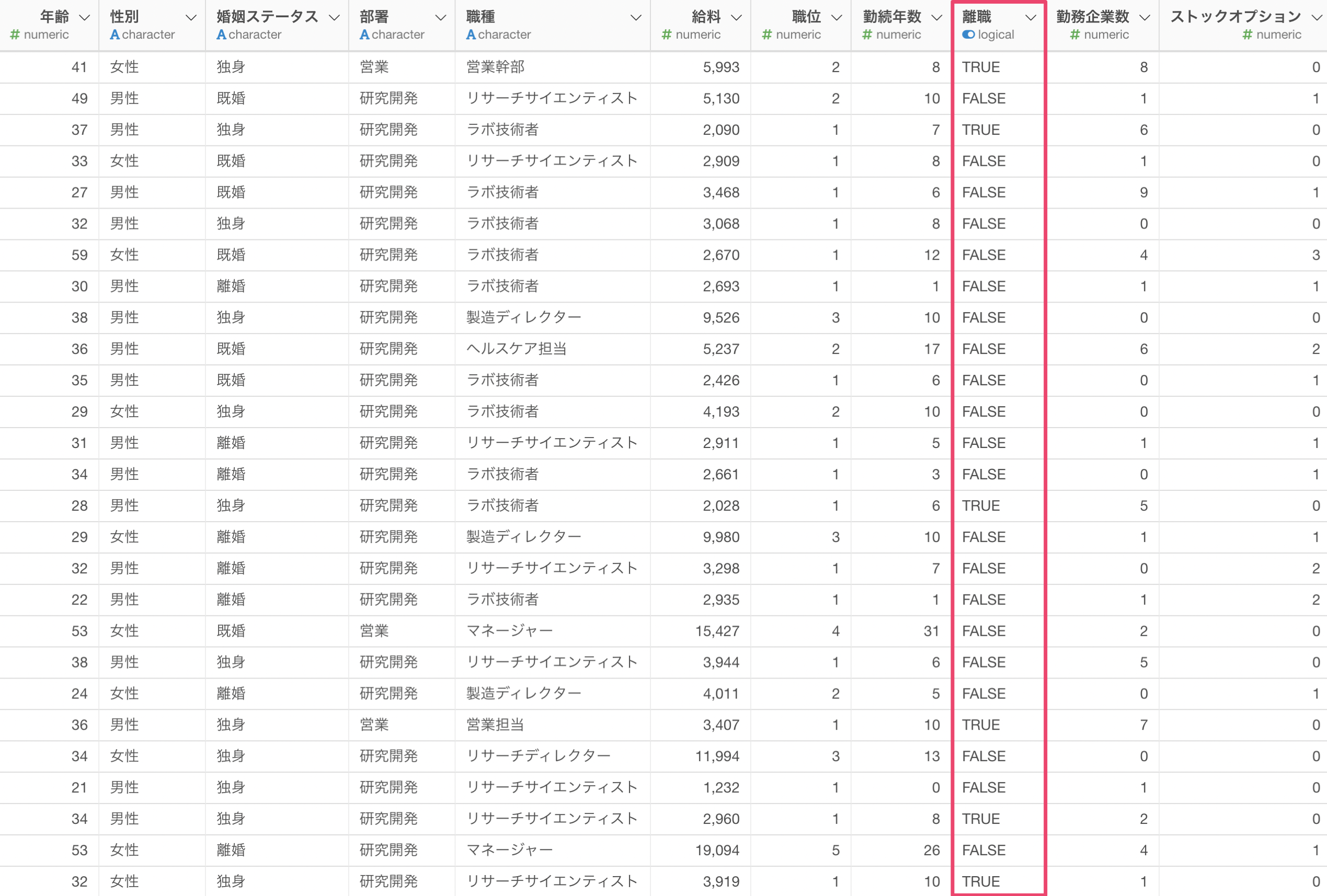
今回は従業員が「離職」しているかどうかを予測するロジスティック回帰のモデルを作成します。
アナリティクスビューを選び、タイプに「ロジスティック回帰」を選択します。
目的変数に「離職」を選択します。
予測変数をクリックします。
予測変数を選択します。Shiftキーを押しながら列を選ぶことで、一気に列を選択できます。
目的変数と予測変数を割り当てることができたら、「実行」ボタンをクリックします。
ロジスティック回帰のモデルが作成されました。
結果の解釈
変数重要度
変数重要度タブでは、どの変数が目的変数とより相関が強いのか、予測する時により重要なのかを調べることができます。
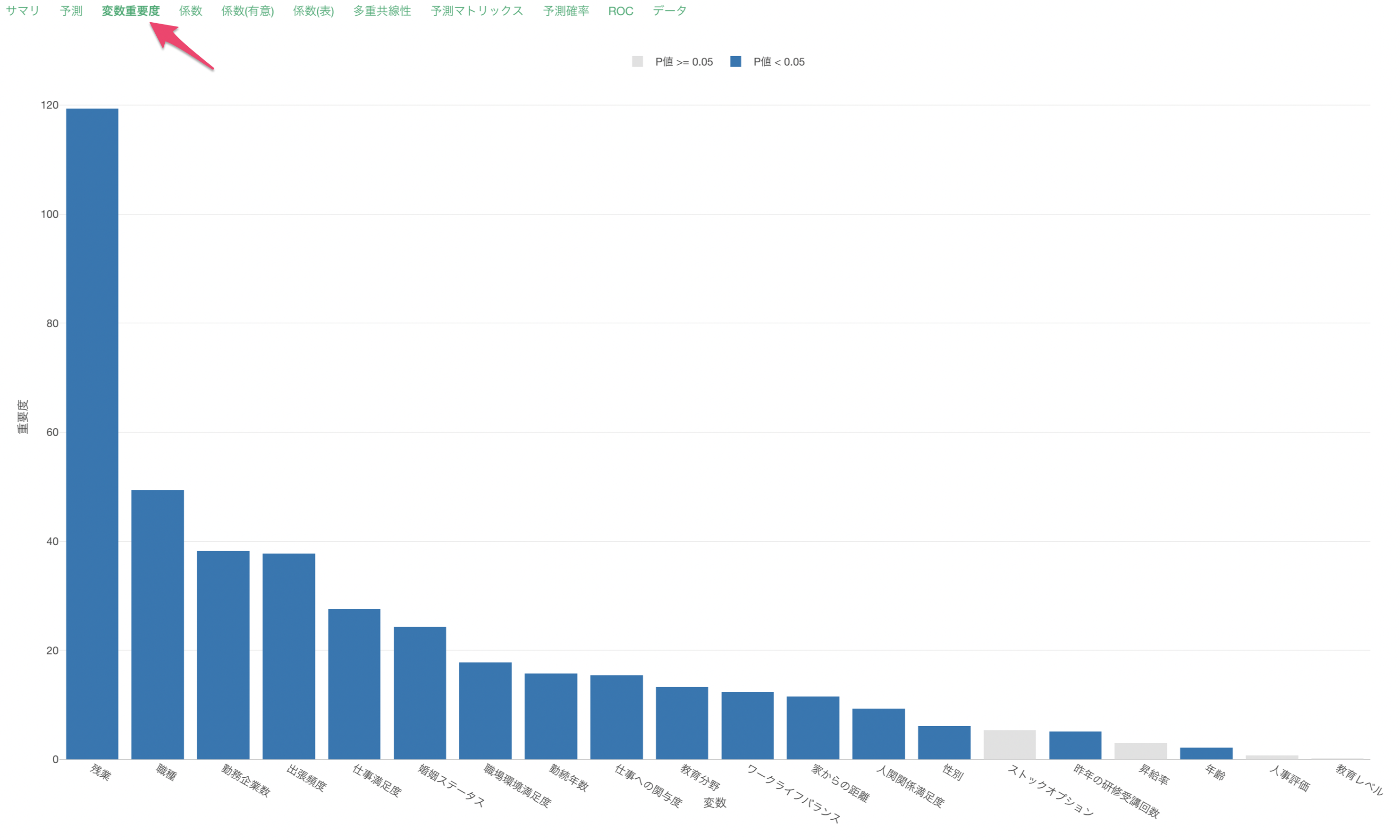
残業が離職を予測する上で最も重要な変数なようです。それ以外にも、職種や勤務企業数などが、離職を予測する上で重要だとわかります。
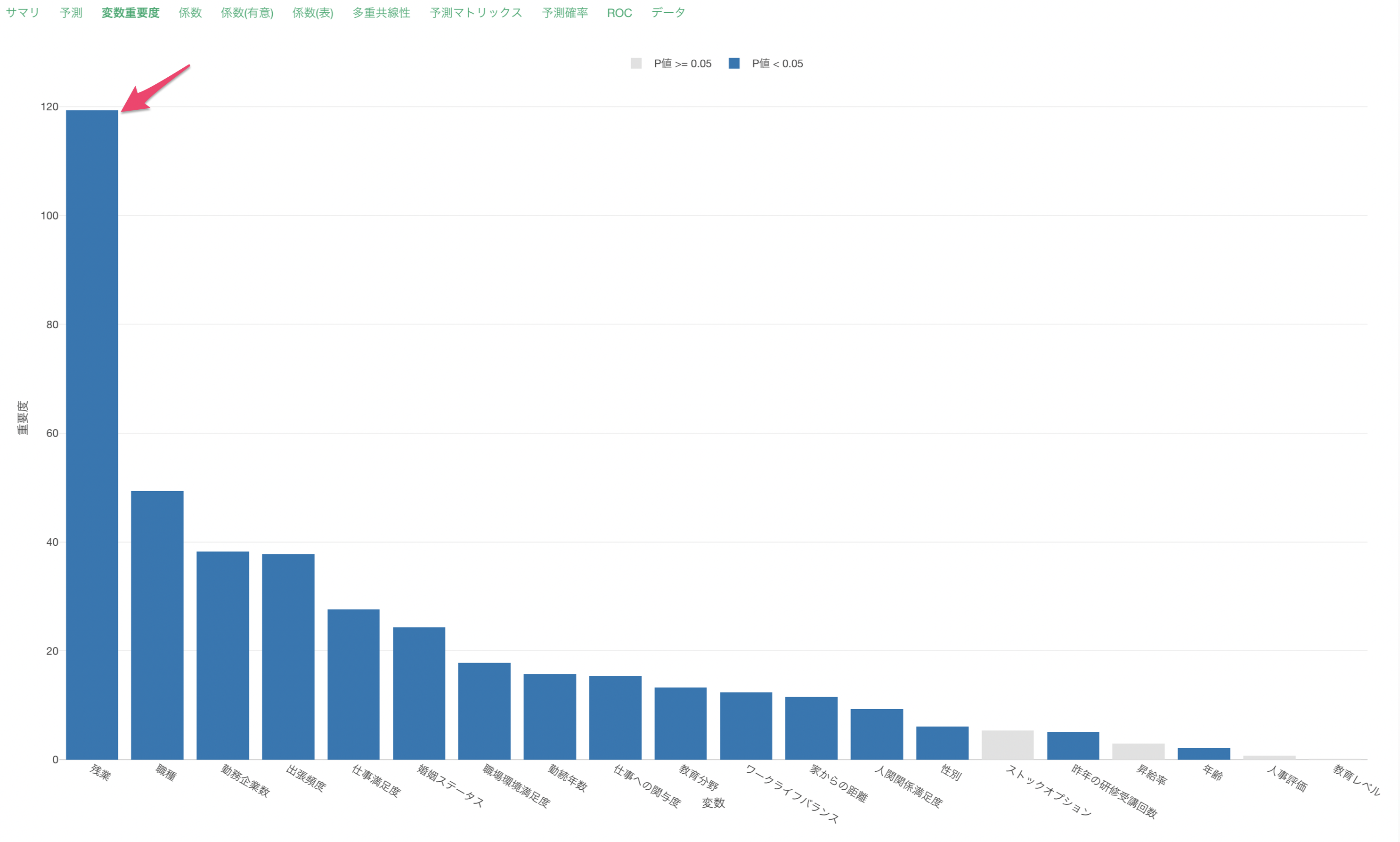
変数重要度の詳しい説明については、こちらの「機械学習モデル - 変数重要度の仕組みと解釈」のセミナーをご覧下さい。
予測
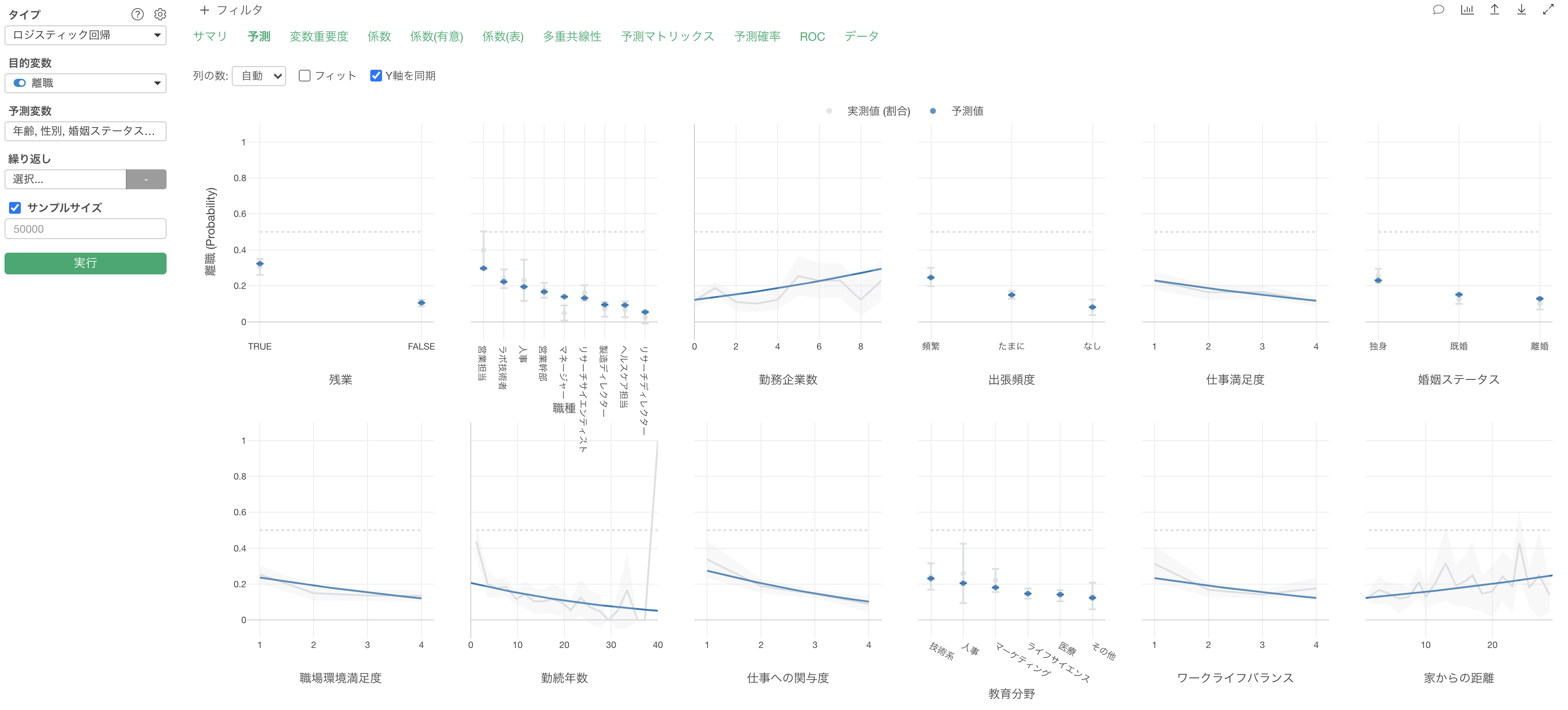
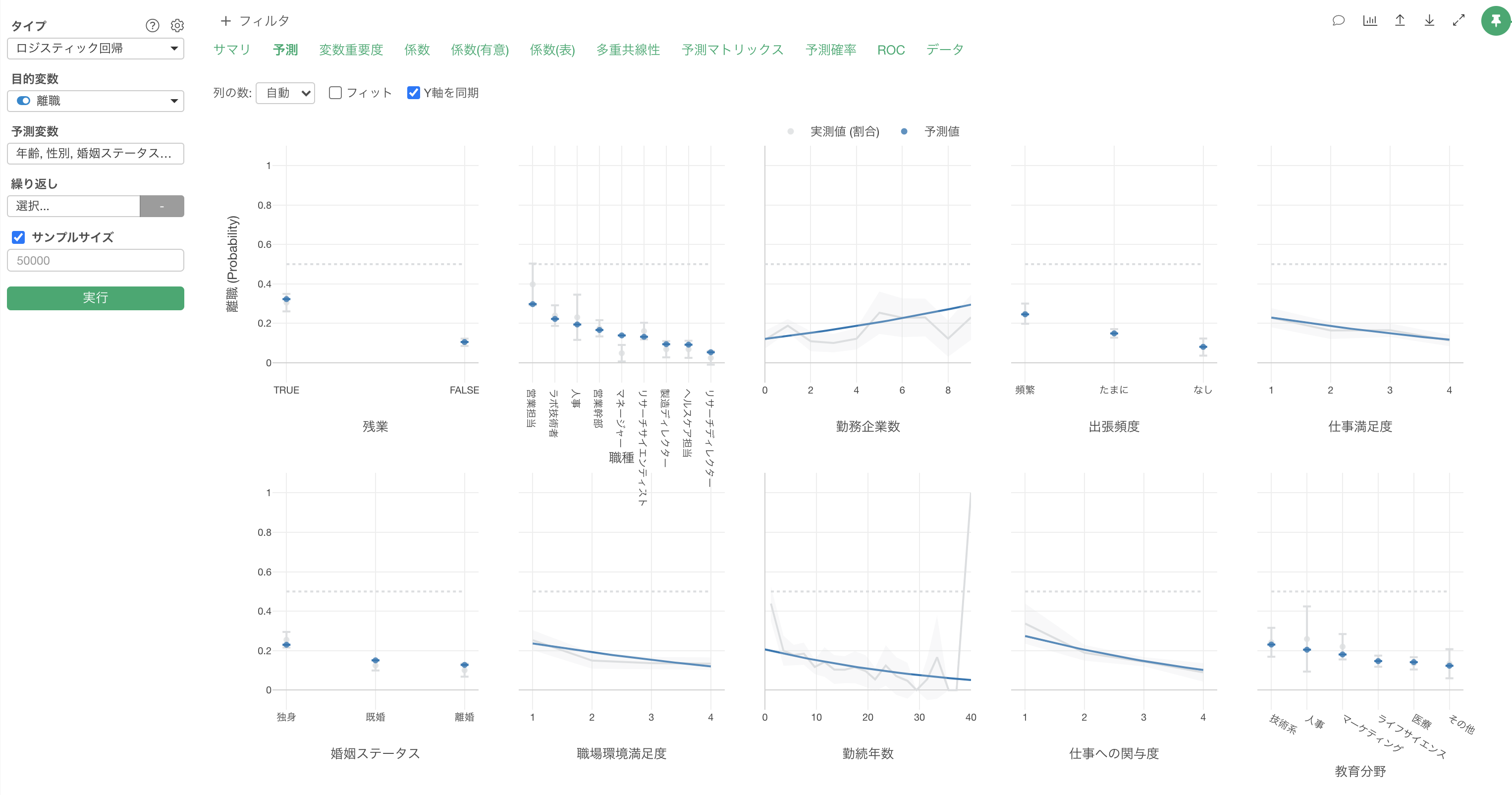
影響度タブでは、それぞれの変数の値が変わると、目的変数の値はどのように変わるのかがわかります。
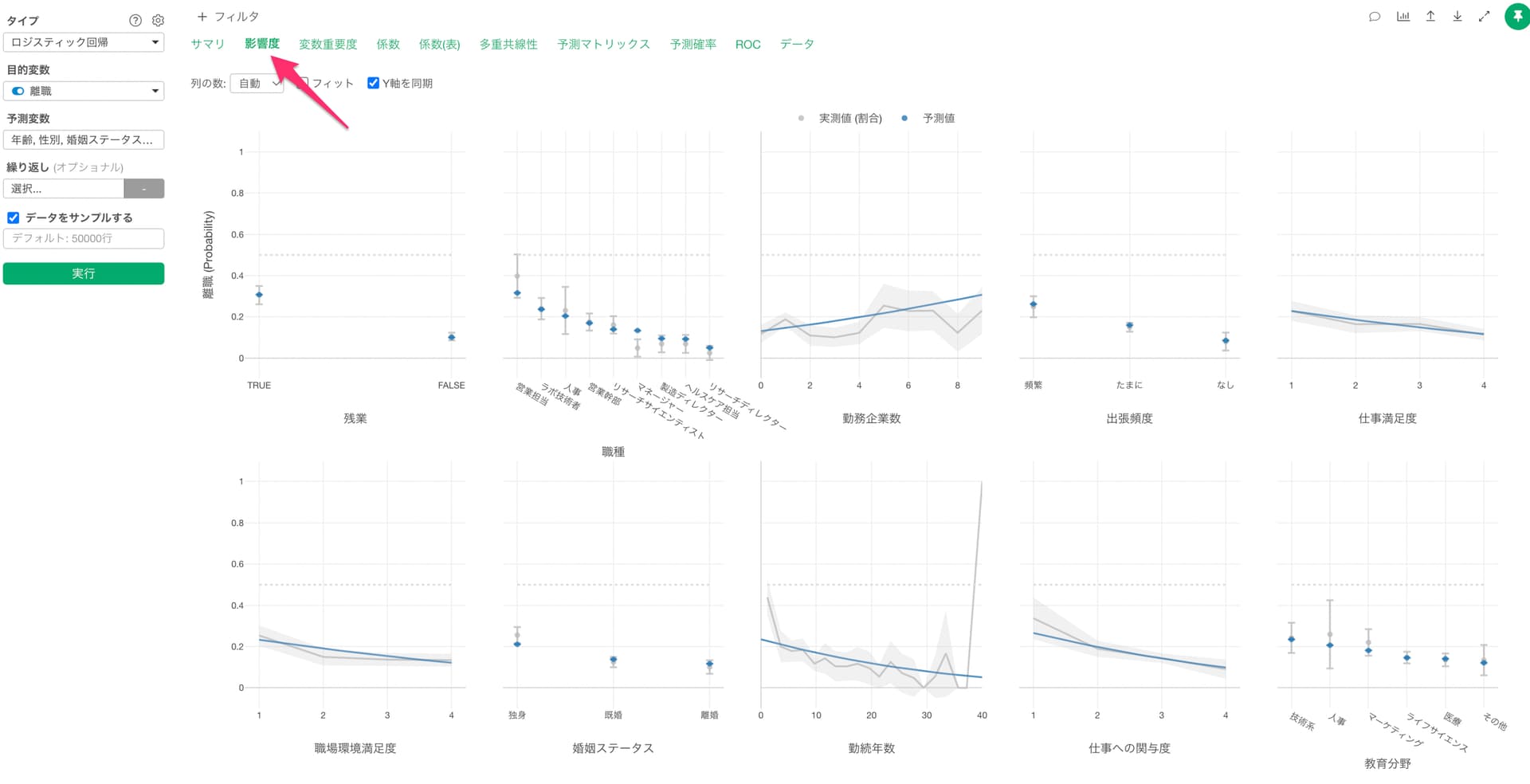
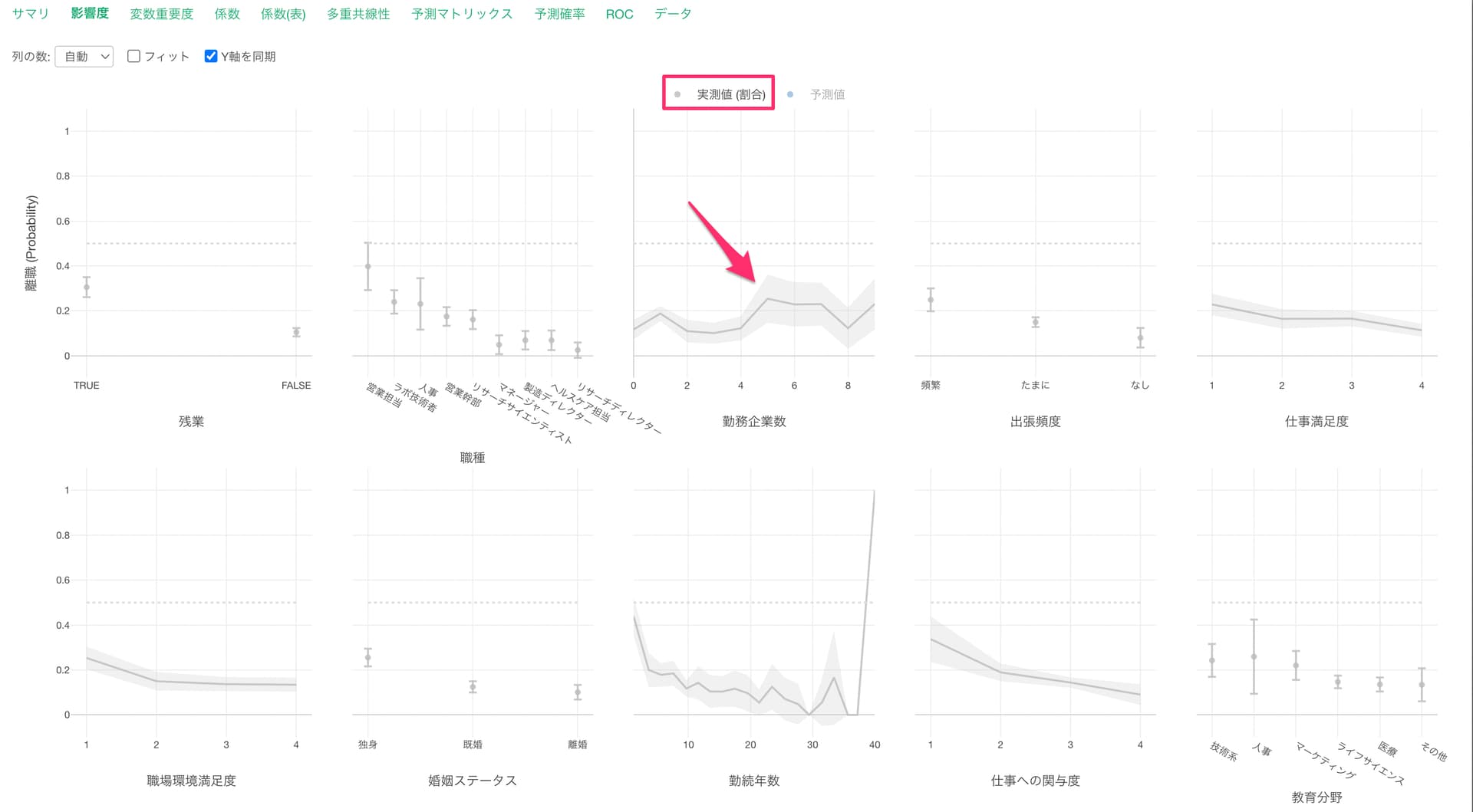
グレーの線は実測値を表しています。
青い線は予測値を表します。
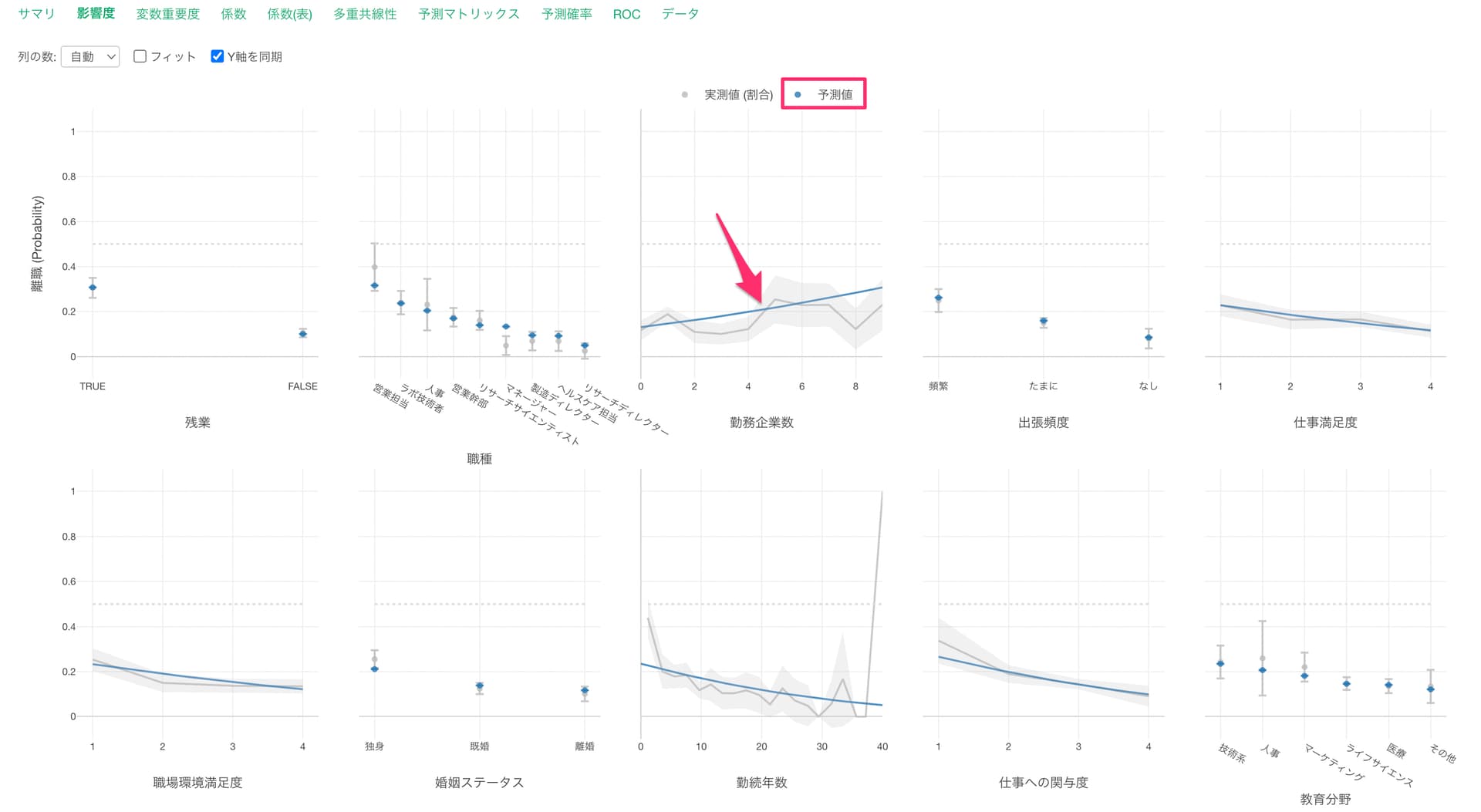
勤務企業数が増えると離職率が高くなる関係があることがわかります。
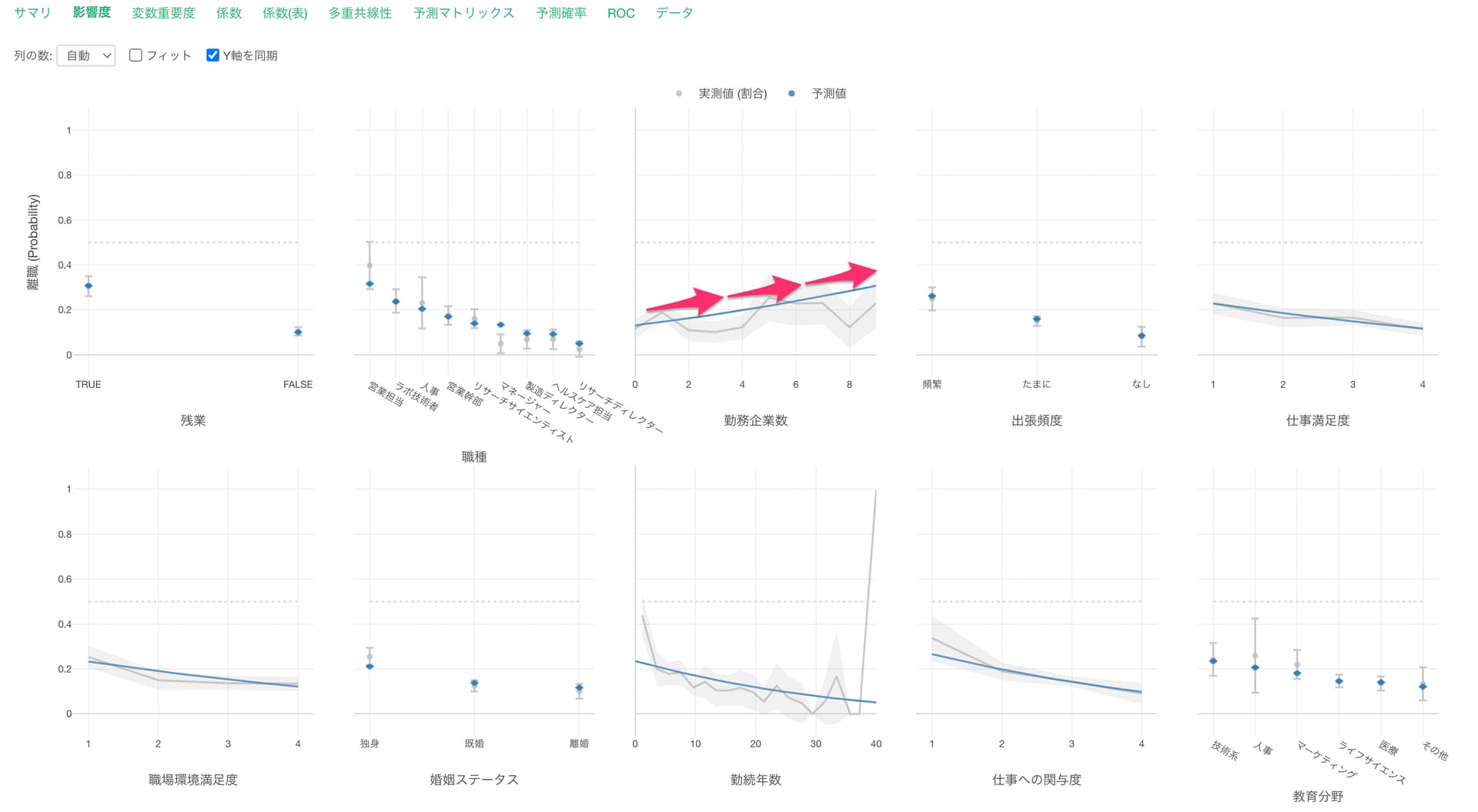
他の変数が一定だった時に、勤務企業数の値が1上がると離職する可能性(オッズ)が1.2004倍になる関係があるようです。
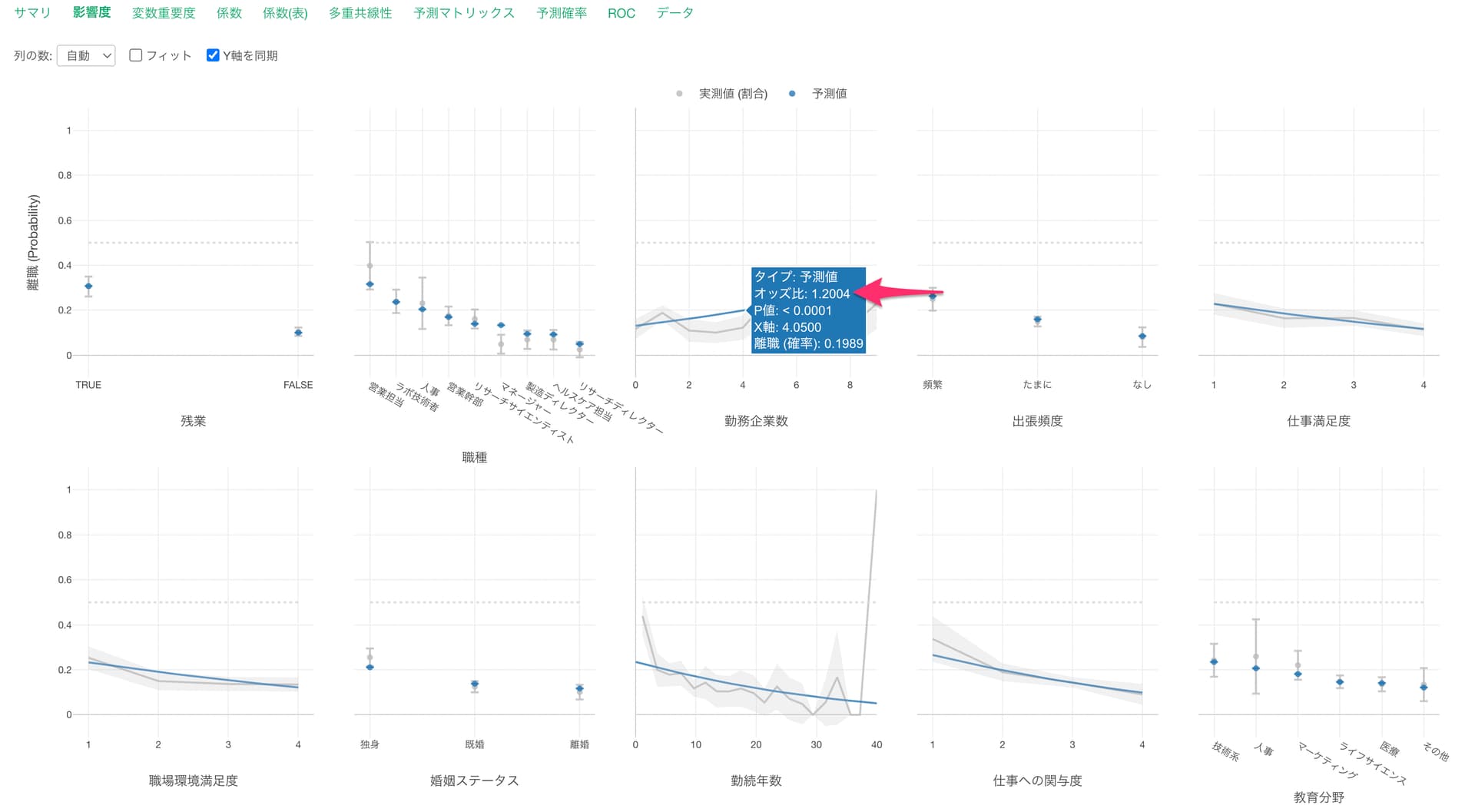
残業で見ると、残業している場合は、していない場合に比べて離職率が高いようです。
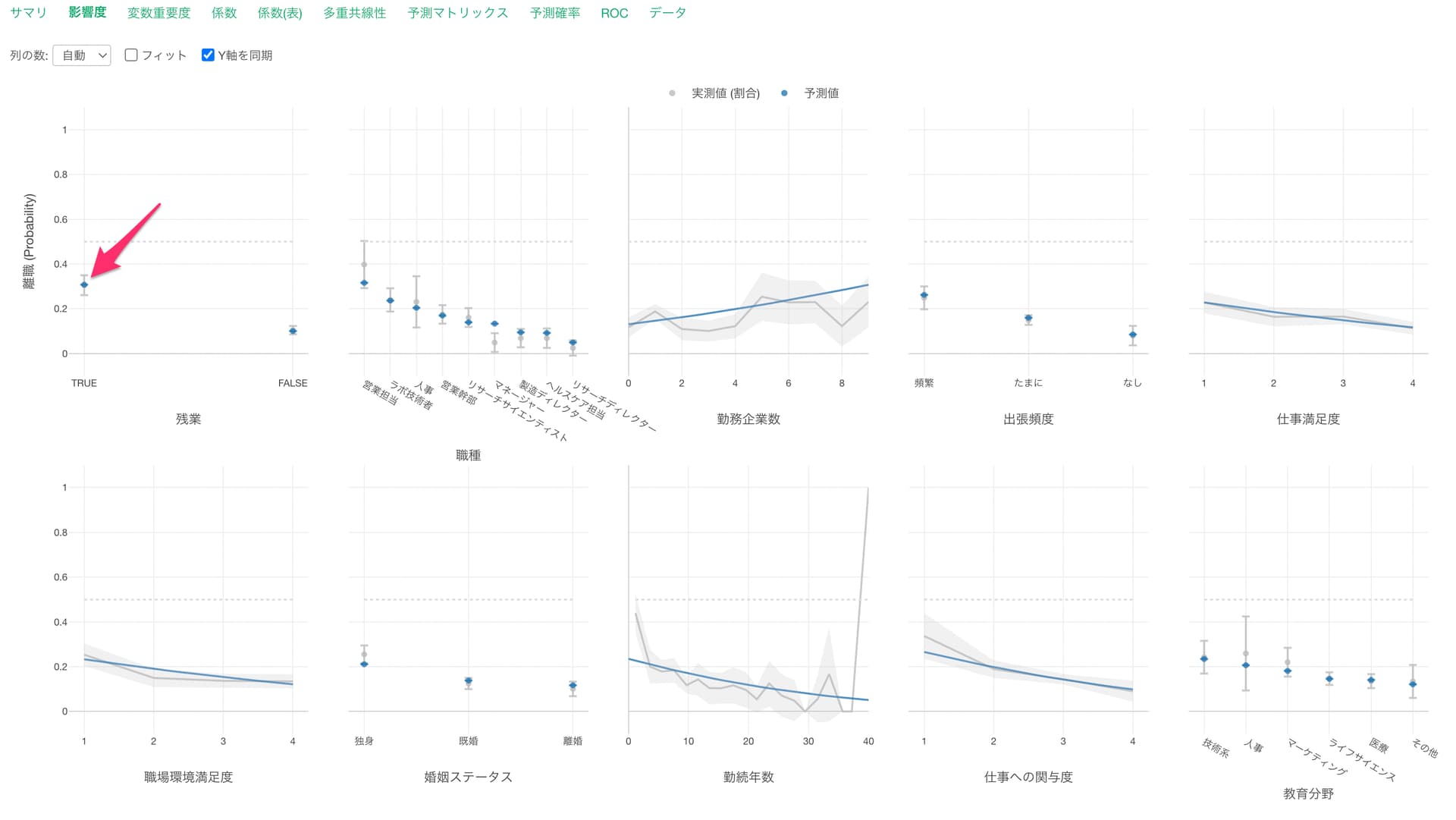
実測値の割合と予測値がずれていることがありますが、これは他の変数の効果が一定だとした時に、その変数での効果を予測しているからになります。
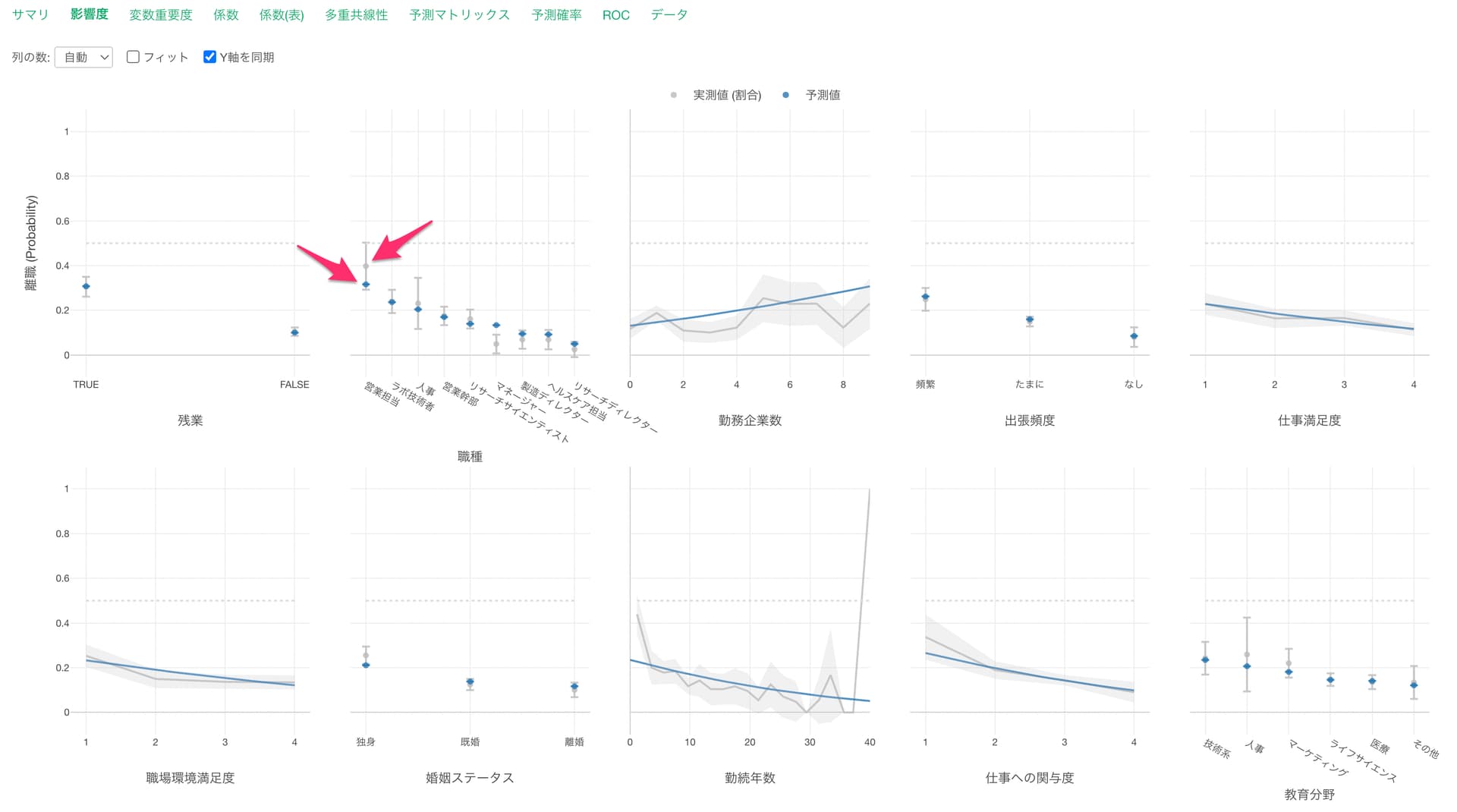
こういった実測値の割合と予測値でずれがある時には、その変数では他の変数と相関が強いことが多いです。
さらに、他の変数の効果を内包していたために、実測値で見た時に効果が高いように見えていたが、実際にはその変数単体で見た時にはそこまでの効果はなかった、またはその逆のパターンが発生することがあります。
係数
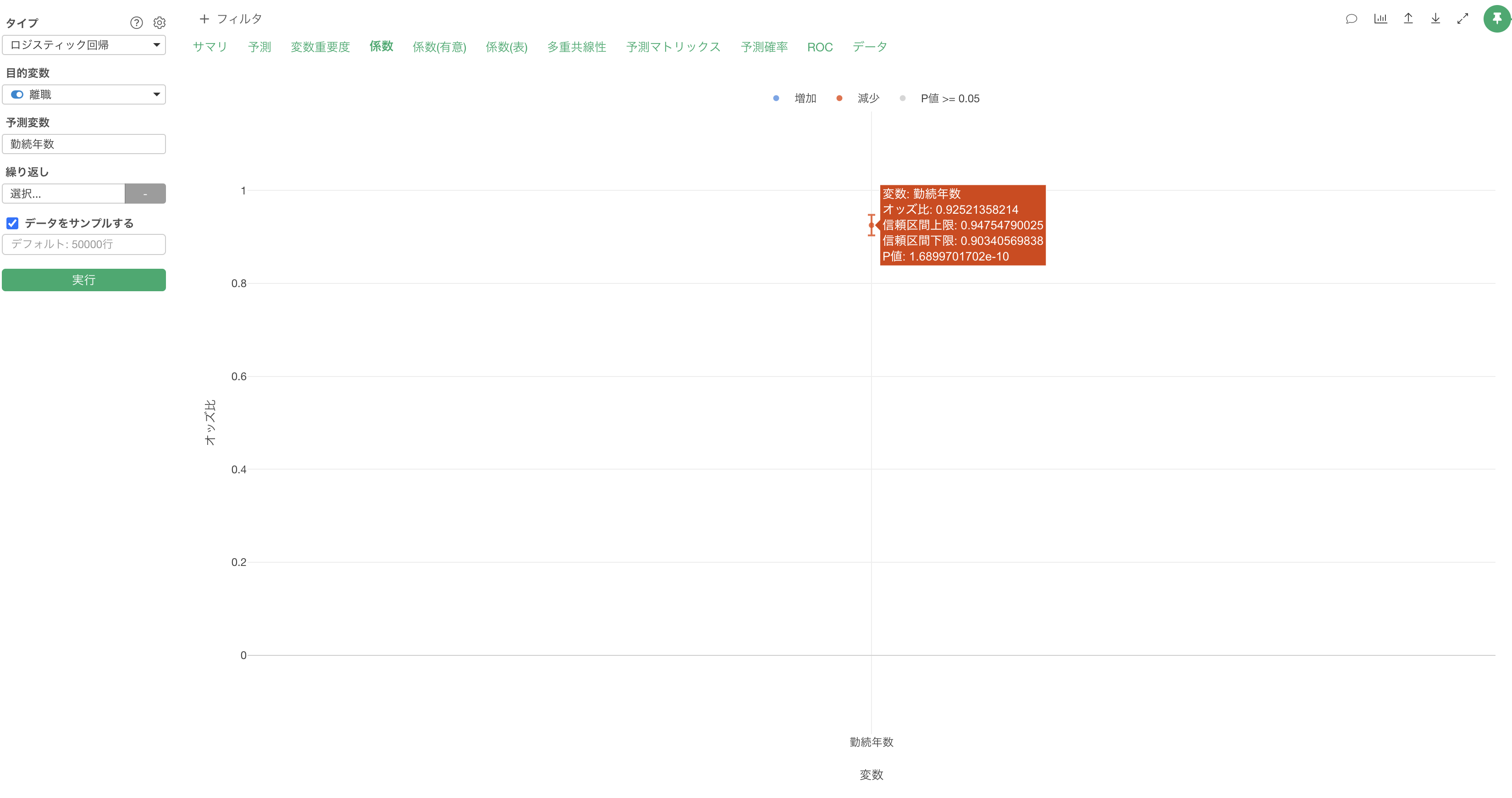
係数タブでは、それぞれの変数のオッズ比とその信頼区間、有意性がわかります。
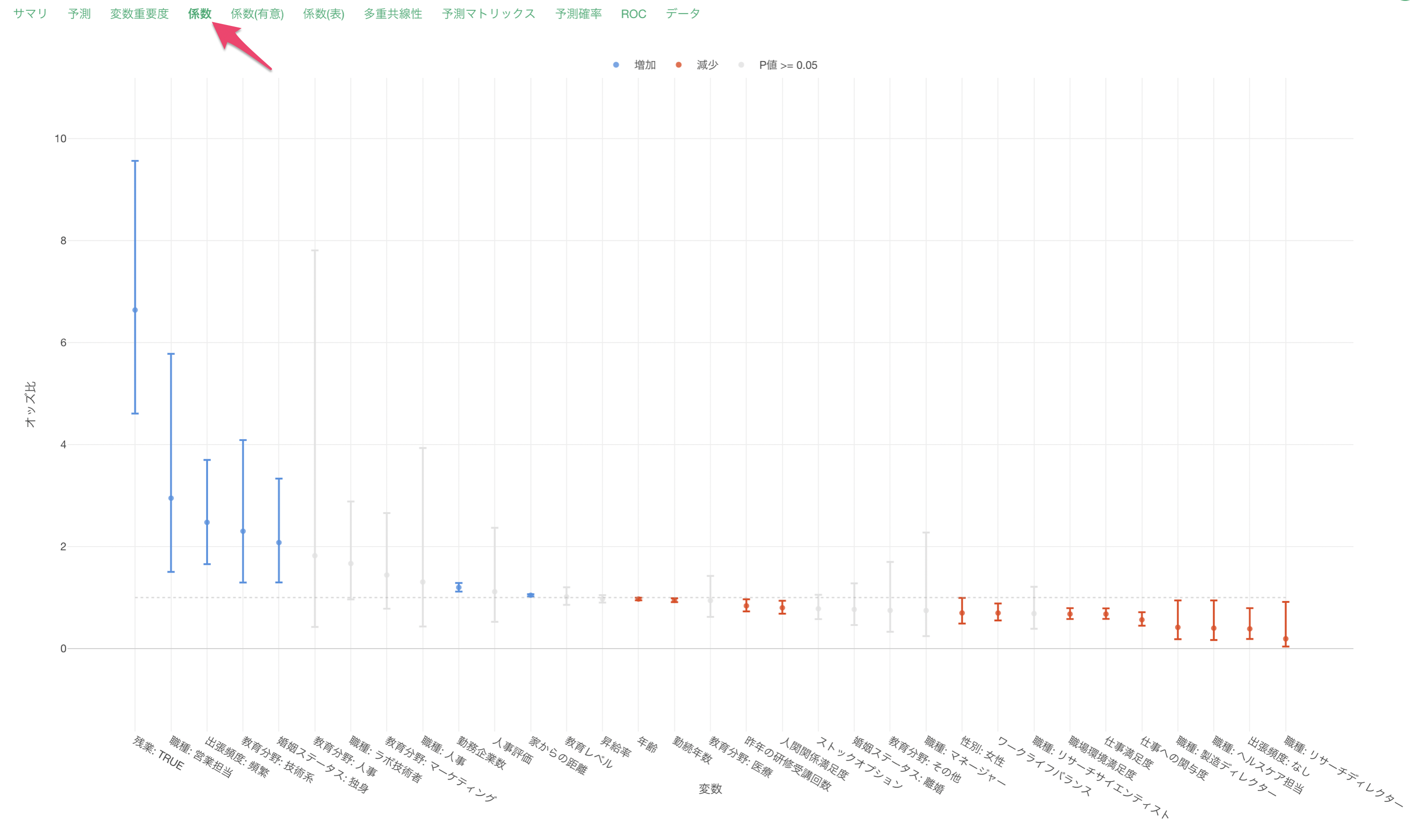
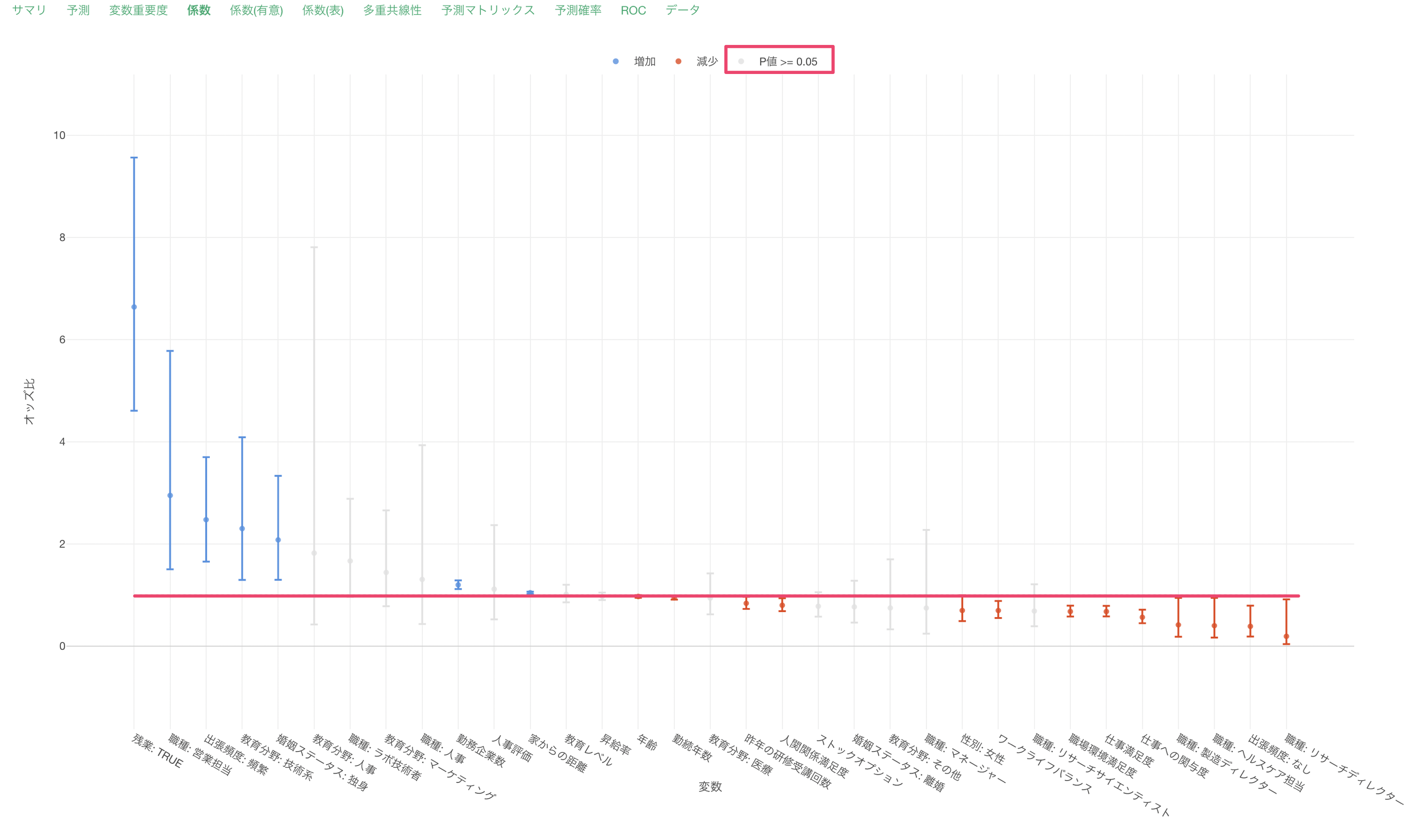
係数が増加(青)または減少(赤)の場合は、目的変数である離職との関係が有意な変数で、P値は5%以下です。これらの有意な変数はオッズ比の信頼区間が1に重なっていない、つまりオッズ比が1であることはないと言えます。
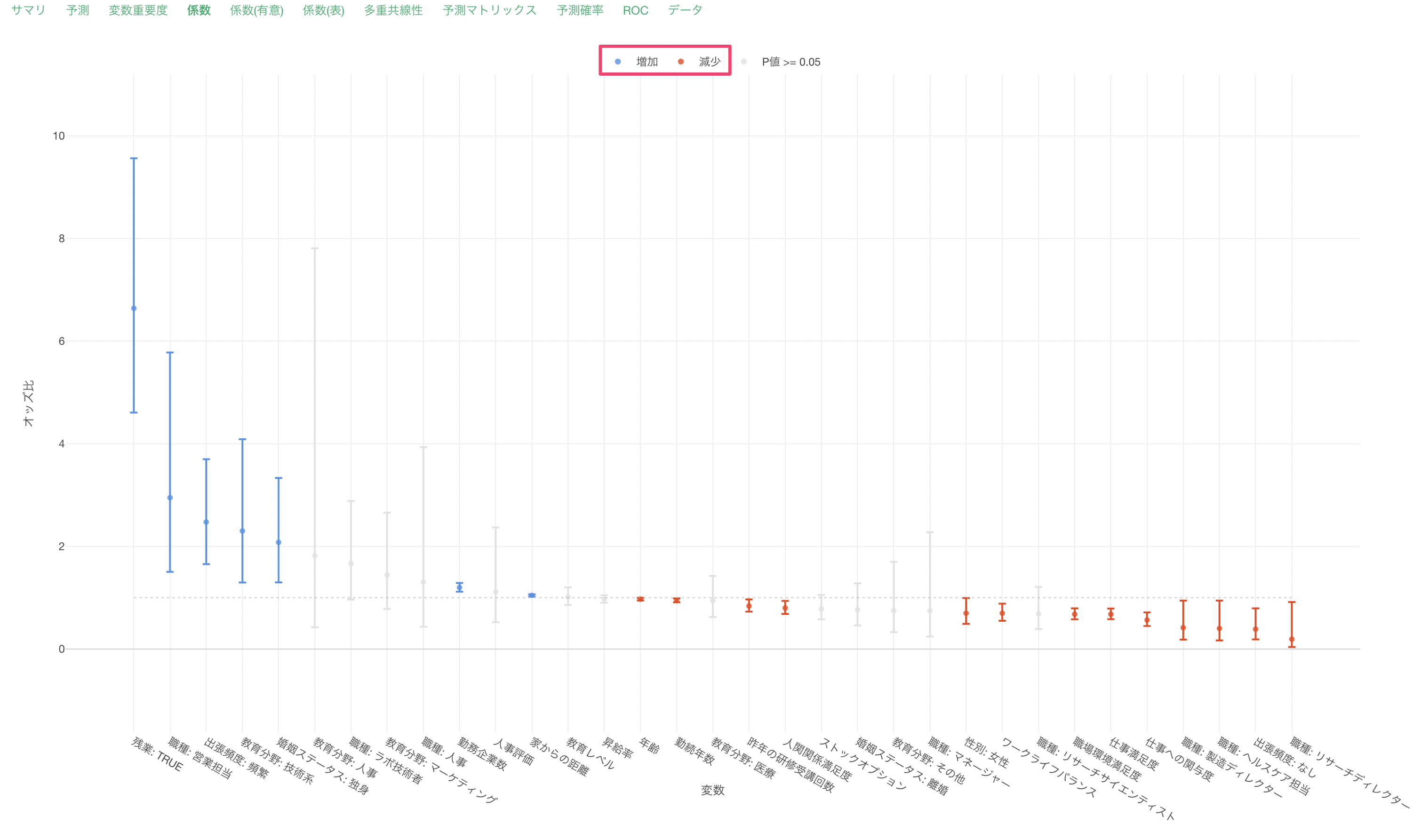
係数がグレーの変数はP値が基準値の5%以上で、統計的に有意であるとは言えない変数です。これらの変数は係数の信頼区間が1に重なっているため、オッズ比が1の可能性があります。
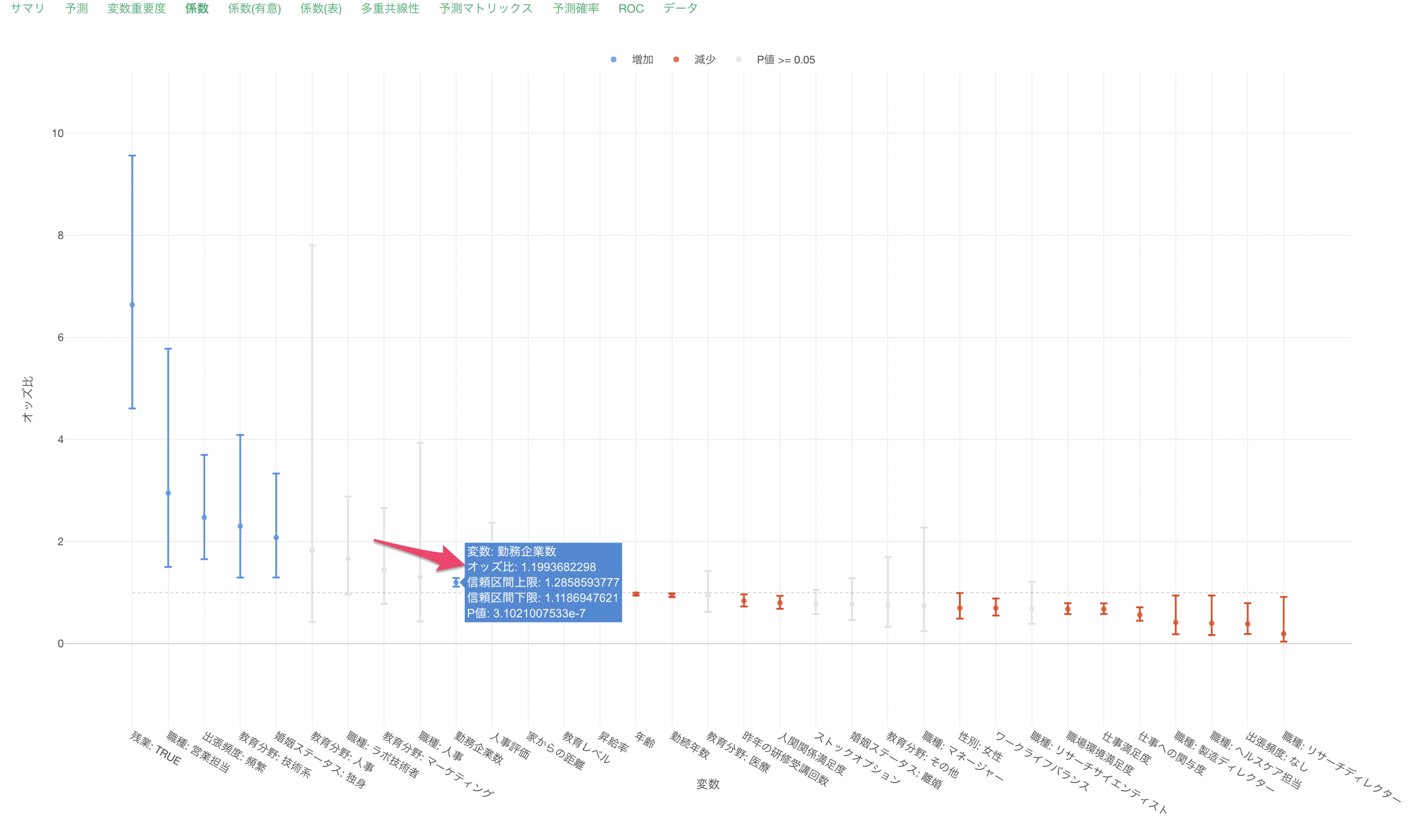
他の変数が一定だった時に、勤務企業数の値が1上がるとオッズ(離職する可能性)が1.2倍になると期待されます。
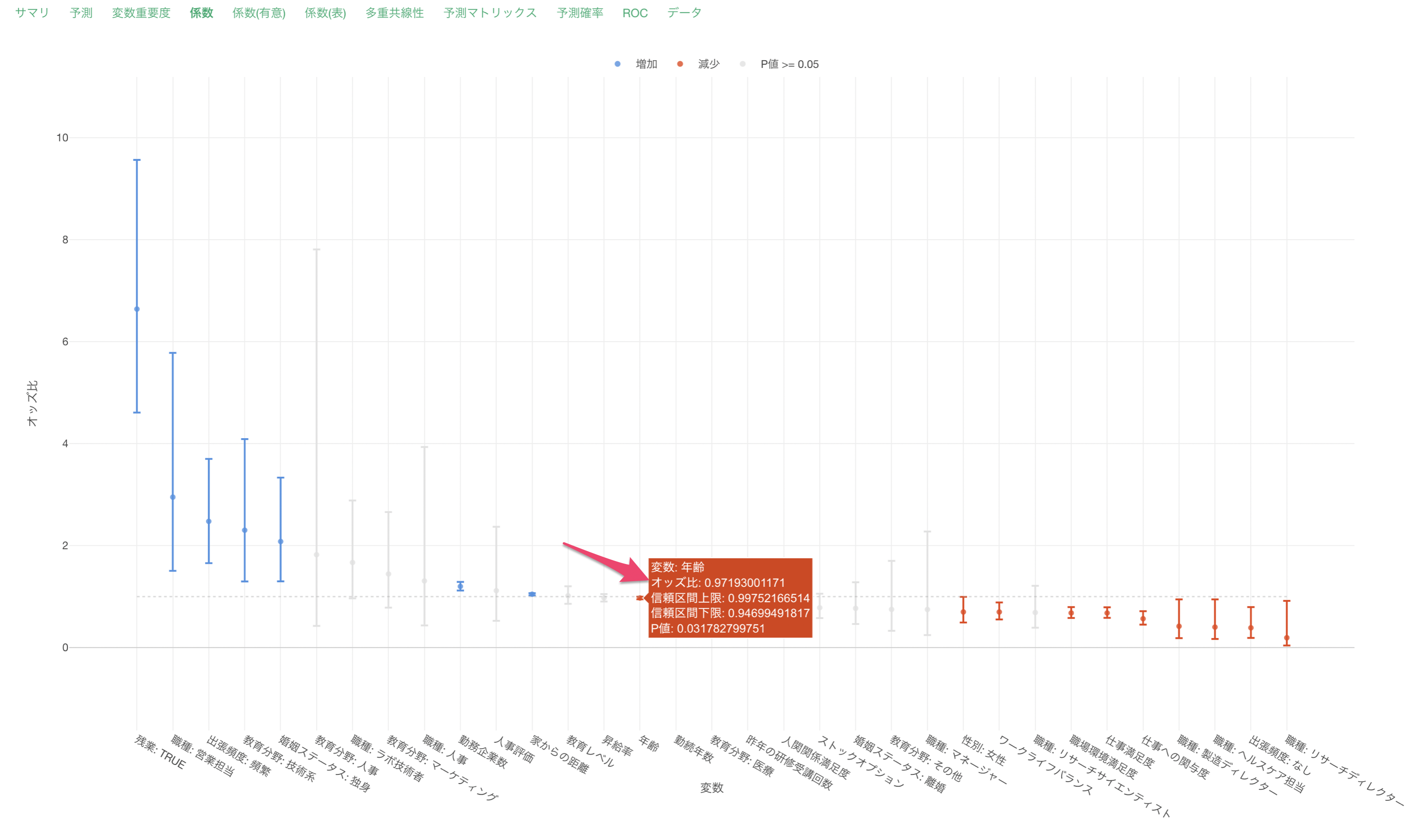
他の変数が一定だった時に、年齢が1歳上がるとオッズ(離職する可能性)が0.97倍になると期待されます。この場合は離職しにくくなるという解釈になります。
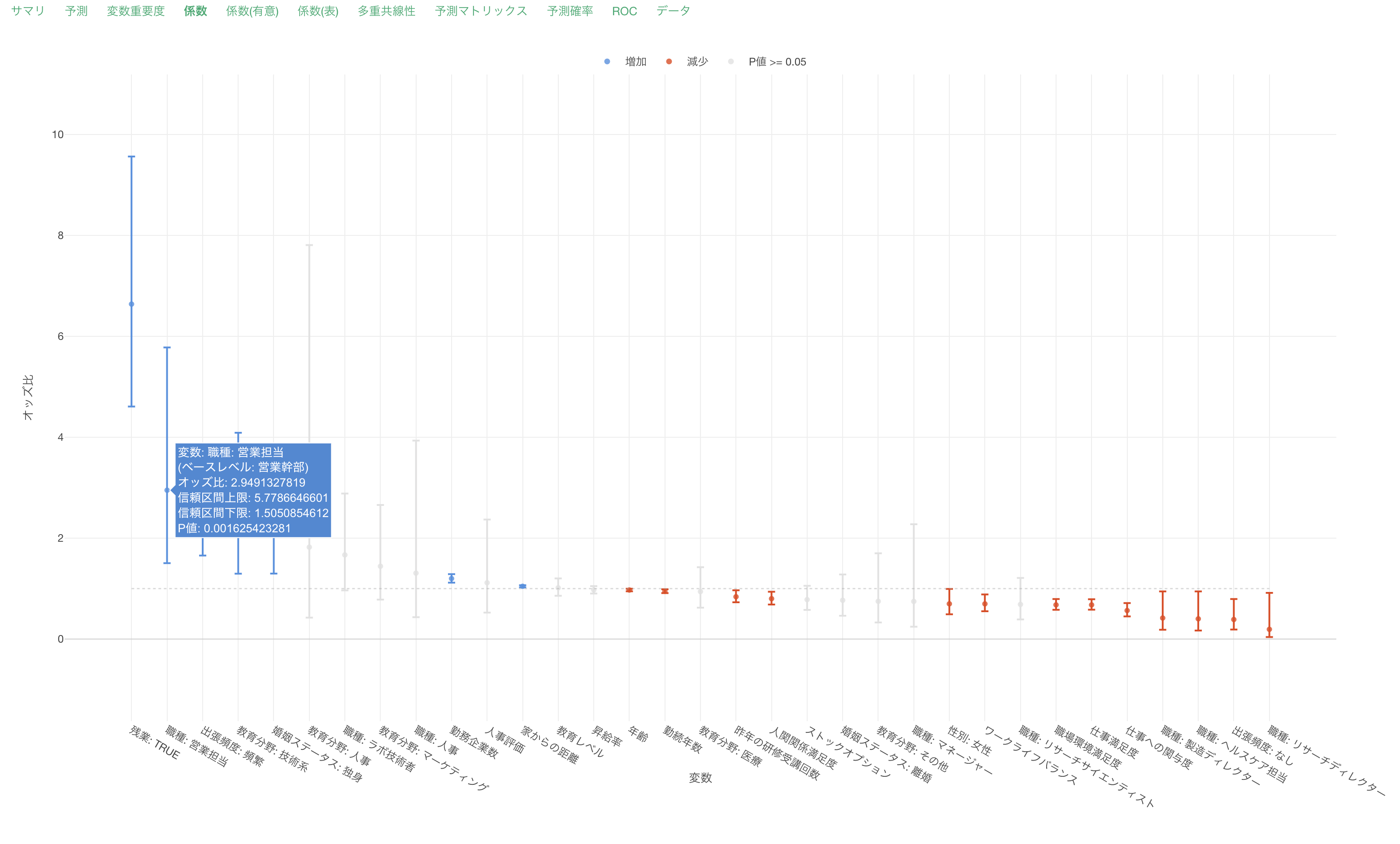
他の変数が一定だった時に、職種が「ベースレベル」である営業幹部から営業担当になるとオッズ(離職する可能性)が2.95倍になると期待されます。
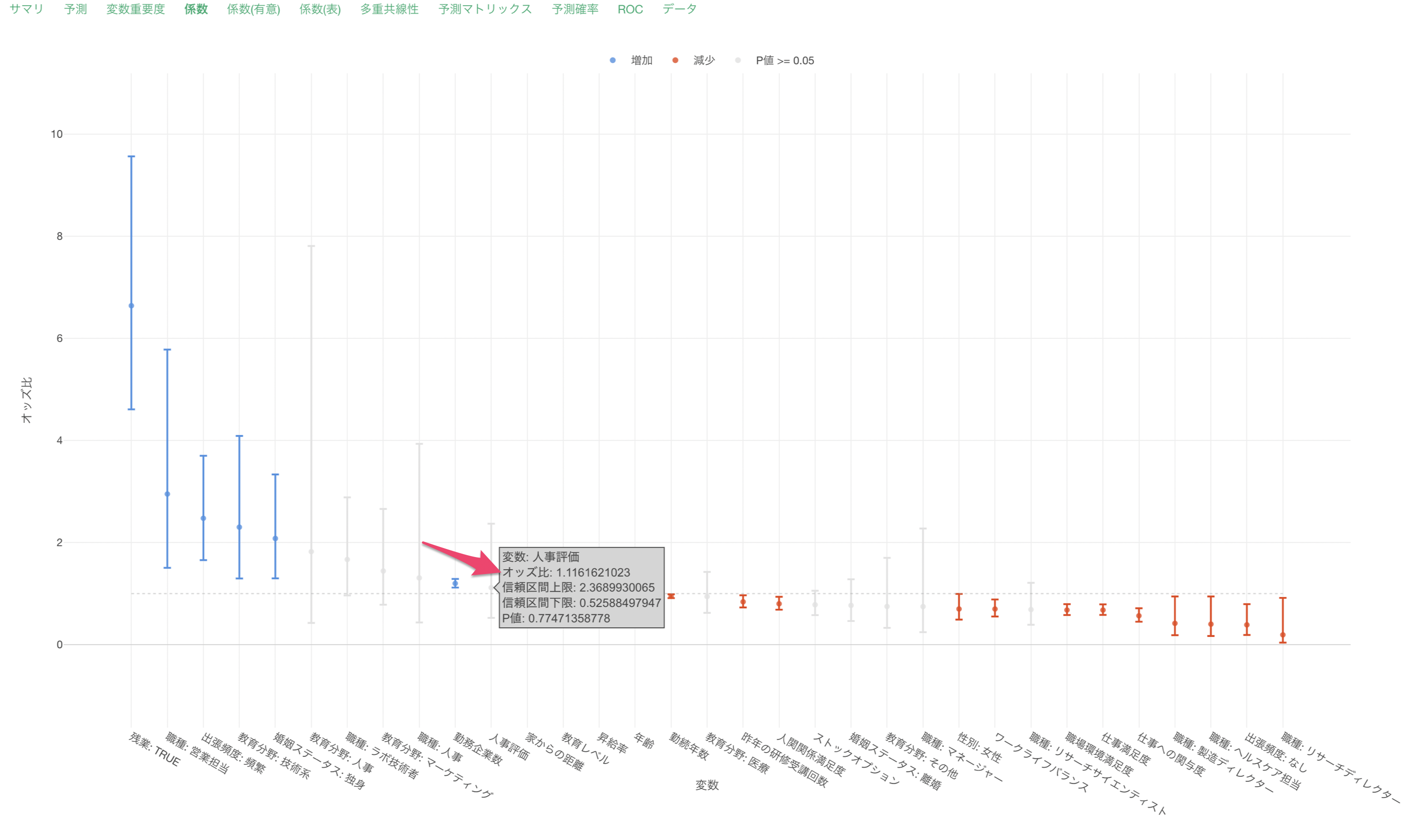
他の変数が一定だった時に、人事評価が1上がるとオッズ(離職する可能性が)と1.16倍になると期待されます。また、人事評価の信頼区間は1をまたいでおり、P値も77%(0.77)と高いため離職に関係があるとは言いきれません。
サマリ
サマリタブでは、この予測モデルの評価を確認できます。

AUCは離職のTRUE/FALSEをこのモデルでどれだけ上手く分けられているかの指標で、0.5から1の間の値を取ります。1に近ければ近いほど、モデルがデータのTRUE/FALSEを上手く分けられていることを示します。

今回は、AUCが0.85と1に近いため、このモデルを使うとTRUEとFALSEを上手く分けられていそうです。
またAUC以外の指標は下記を表しています。

F値
後述する適合率と検出率の調和平均です。0から1の間の値をとり、1に近いほど良い指標です。
正解率
実測値と予測値を比べたときに予測値が正解だった割合です。
誤分類率
予測値と実測値を比べたときに予測値が不正解だった割合です。タイプ1エラー(第一種過誤/偽陽性/False Positive)とタイプ2エラー(第二種過誤/偽陰性/False Negative)を足すと誤分類率と等しくなります。
適合率(Precision)
「TRUE」と予測したデータの中で、実際に正解が「TRUE」だった割合です。
検出率(Recall)
実測値が「TRUE」のときに、予測モデルが「TRUE」と予測できている割合です。
上記の指標につきましては下記のセミナーで詳細をご紹介していますので、ご参考ください。
- ロジカル型予測モデルの評価指標: AUC & F値 - リンク
予測確率
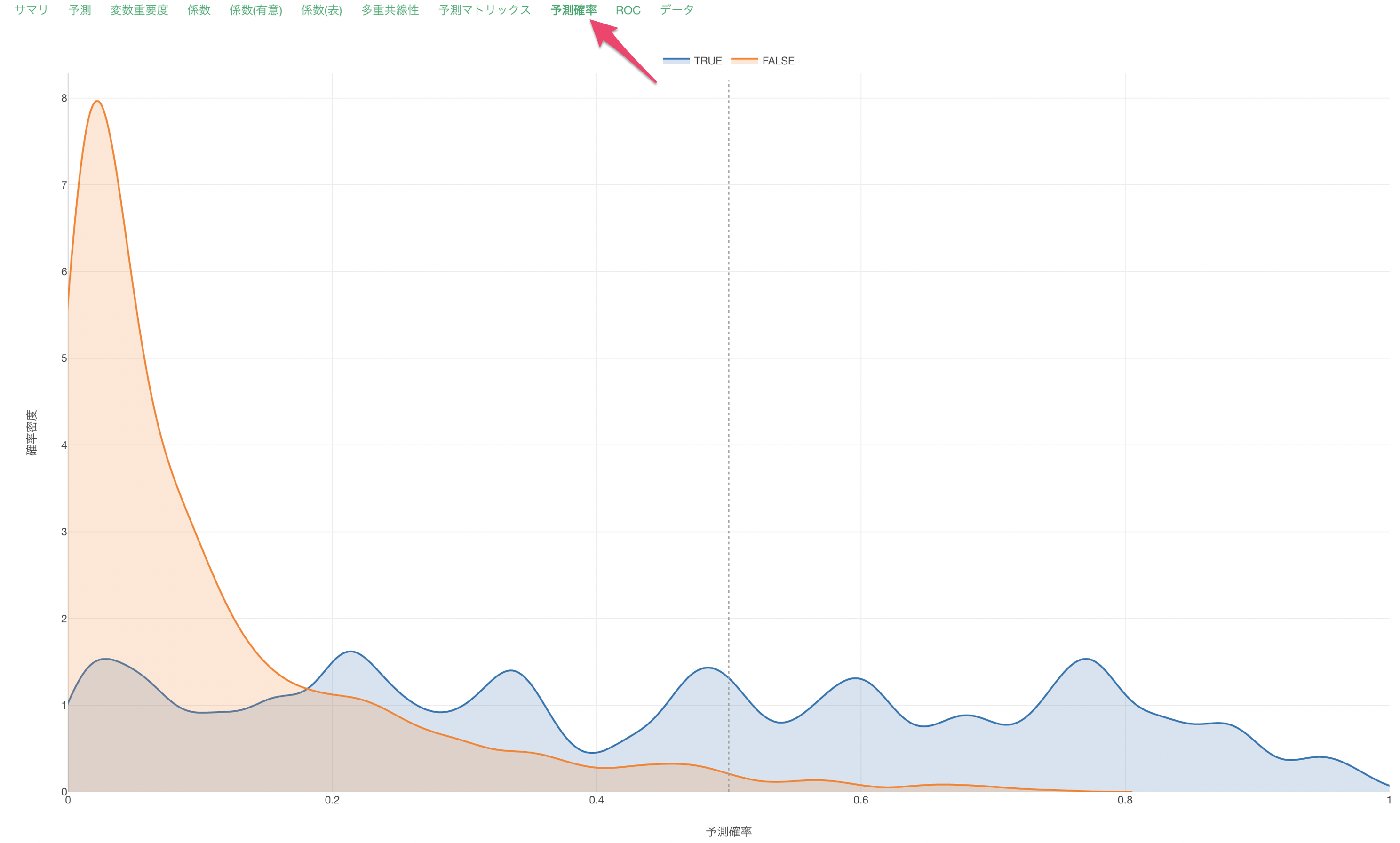
予測確率タブでは、このロジスティック回帰のモデルで離職を予測した確率を、実際のデータでTRUEだったとき、FALSEだったときに分けて、それぞれ分布(密度曲線)にして可視化しています。
ROC
ROCタブでは、AUCの元となる面積をROC曲線から確認できます。
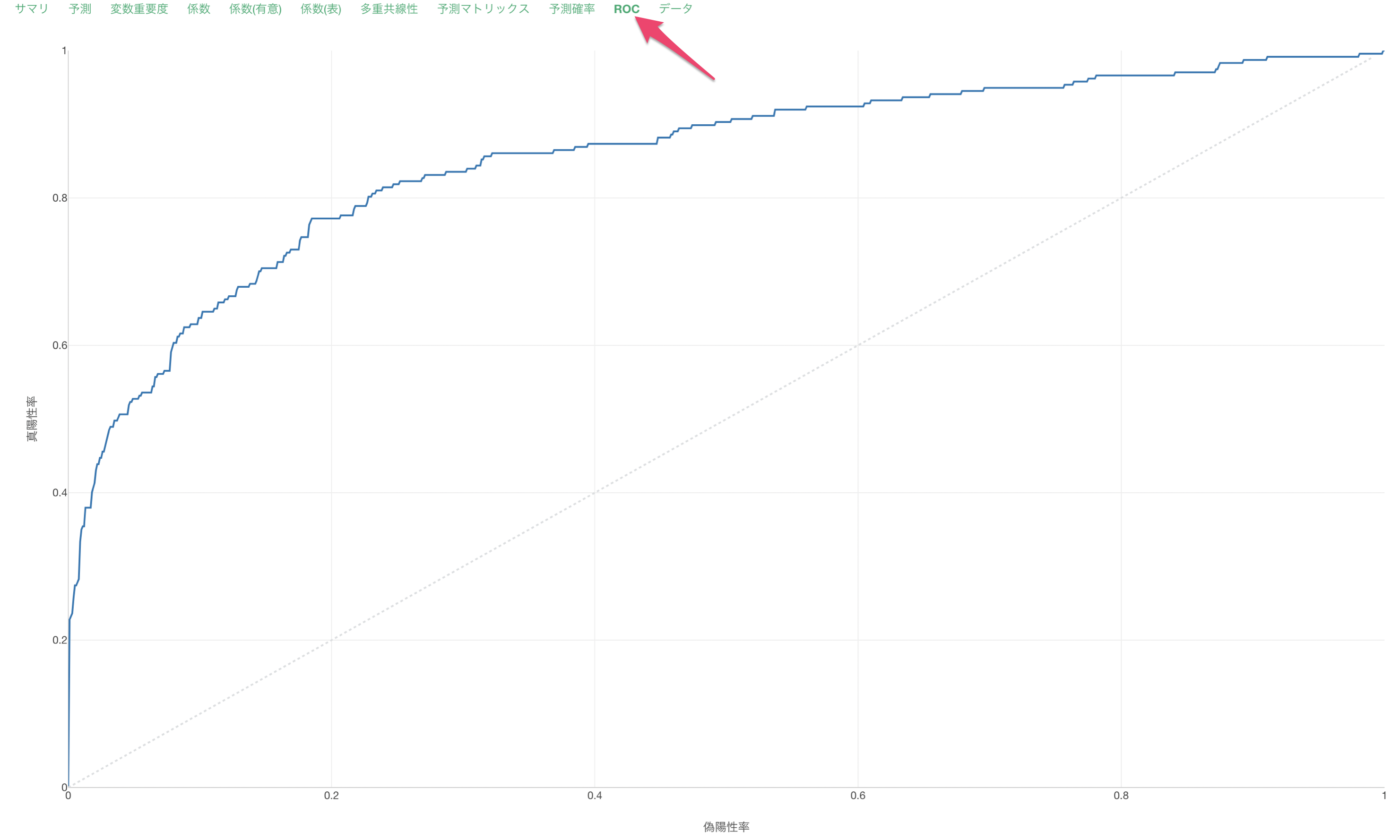
AUCが低い時はROC曲線が対角線上に近づいていきます。
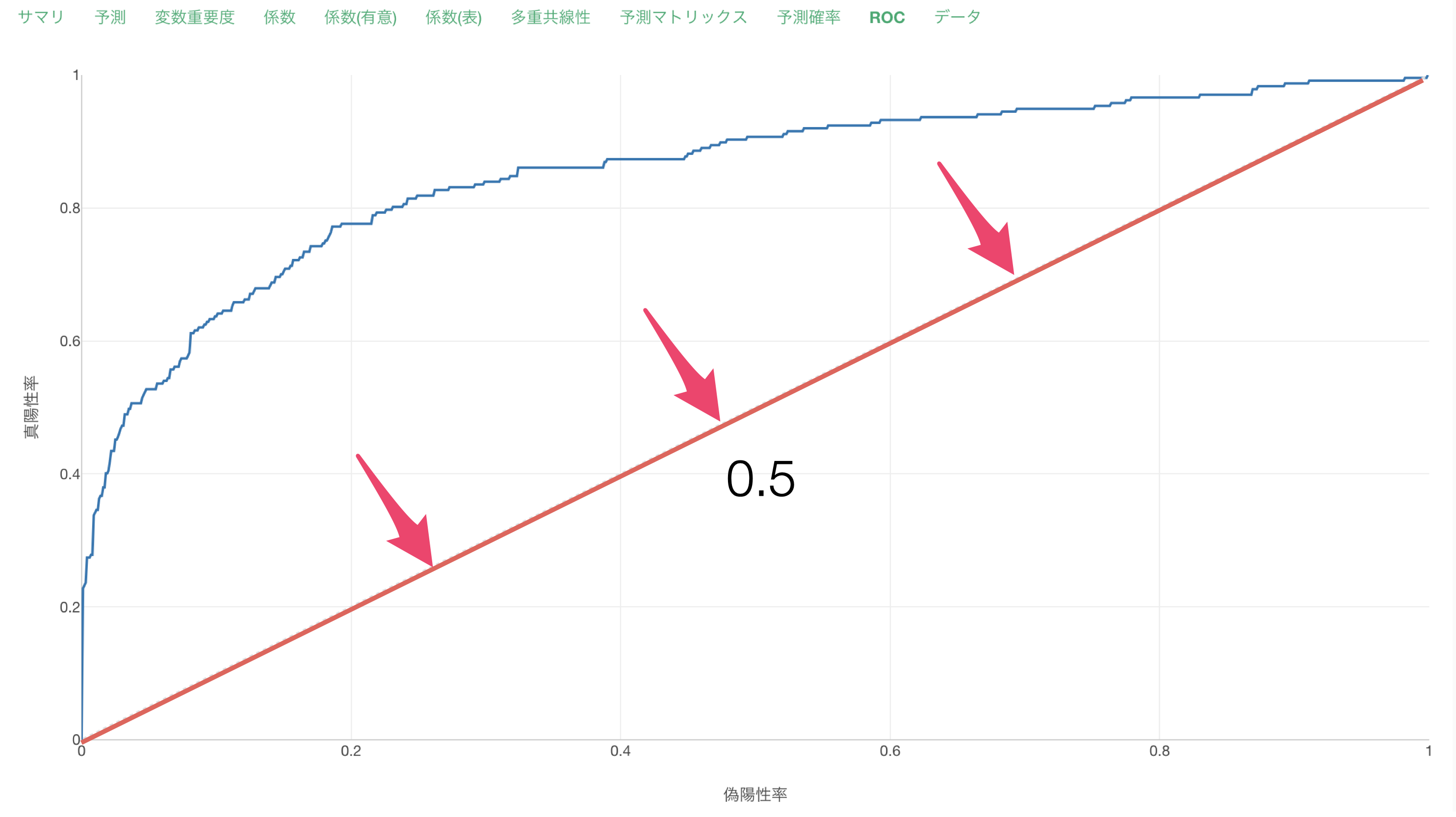
AUCが高い時はROC曲線が直角に近づいていきます。
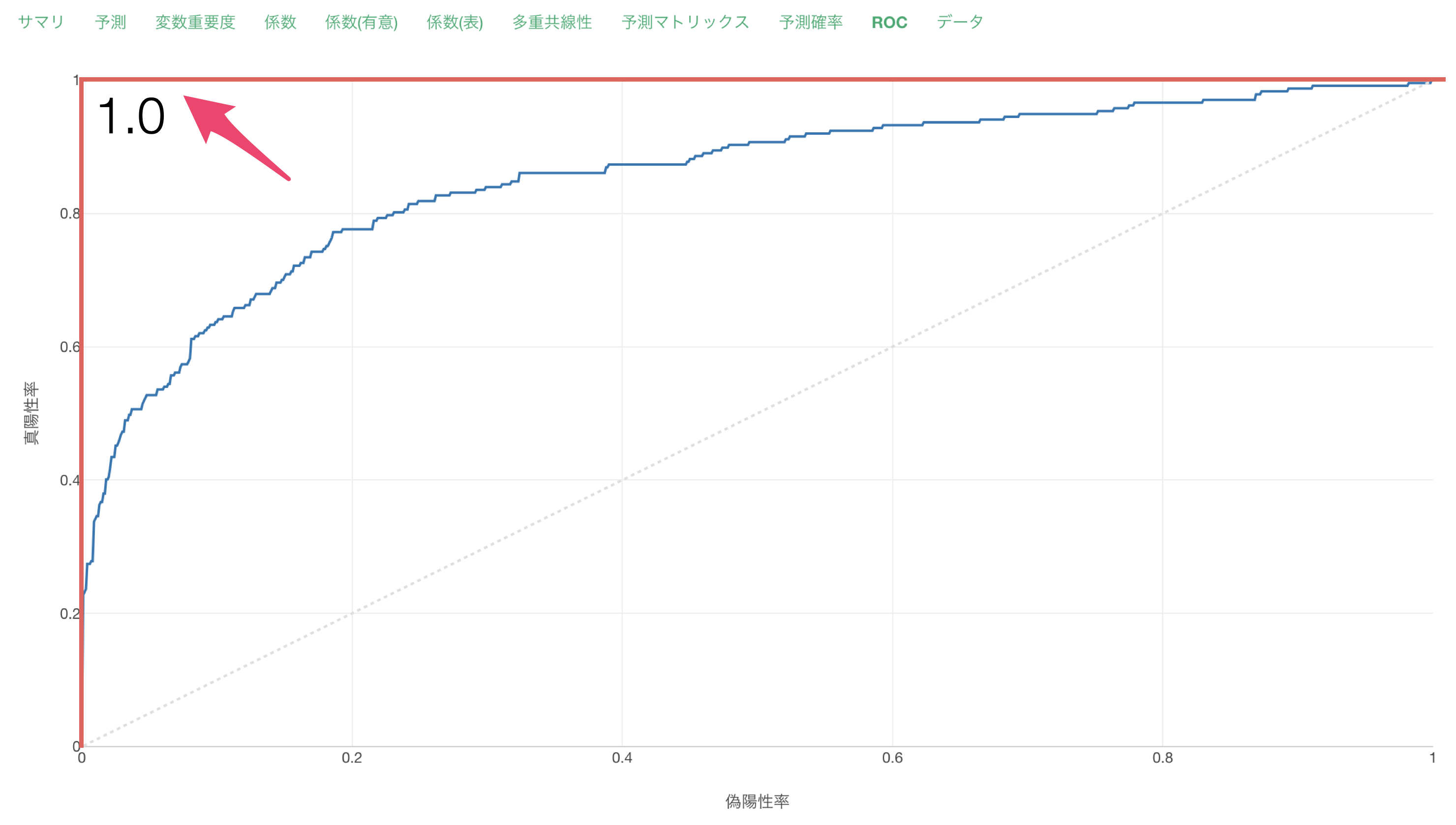
データ
データタブでは、モデルに使用したデータと予測値をテーブル形式で表示されます。
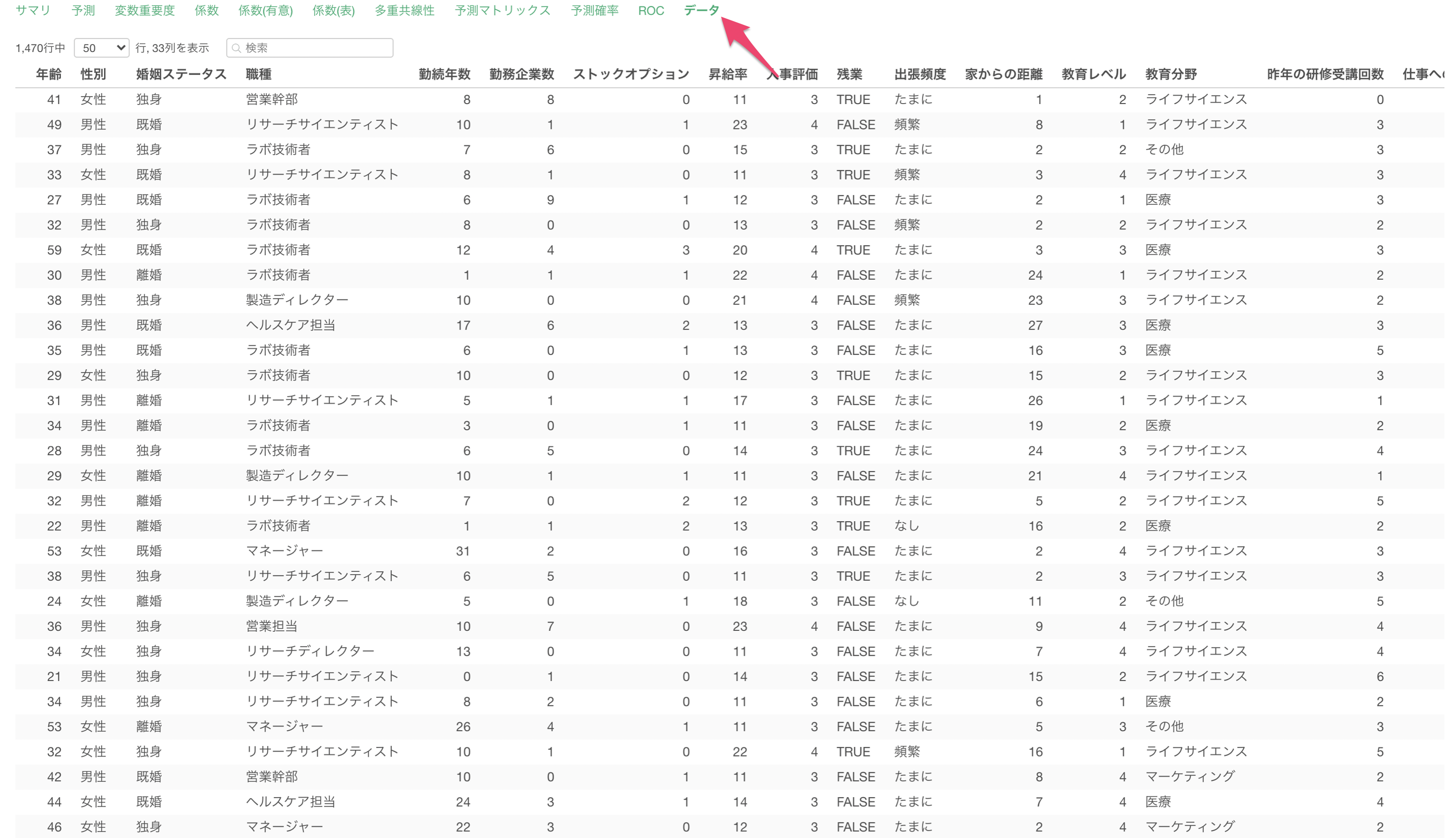
目的変数である離職と、このモデルで算出された予測値(Predicted Value)と閾値を元にしたTRUE/FALSEのラベル(Predicted Label)を確認できます。
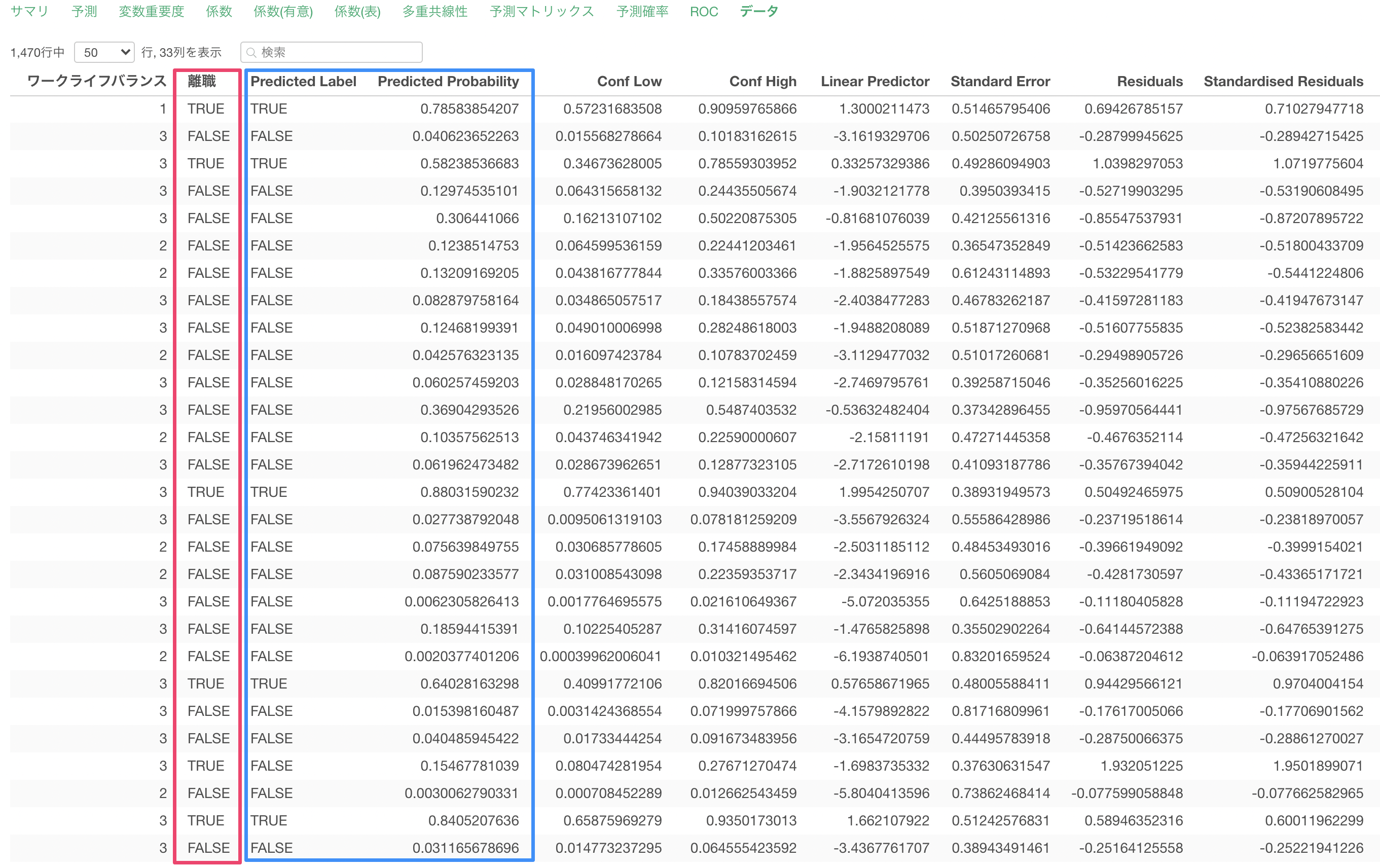
参考資料
ロジスティック回帰に関する参考資料は下記をご覧ください。
ロジスティック回帰に関するよくある質問
オッズは何を表していますか
TRUEの確率がFALSEの確率に比べて何倍かを表しており、下記のように計算することができます。
オッズ = TRUEの確率 / FALSEの確率例えば、コンバートするかしないかに関するデータがあった時には、オッズは下記のように求められます。

予測変数が数値型の時のオッズ比は何を表していますか
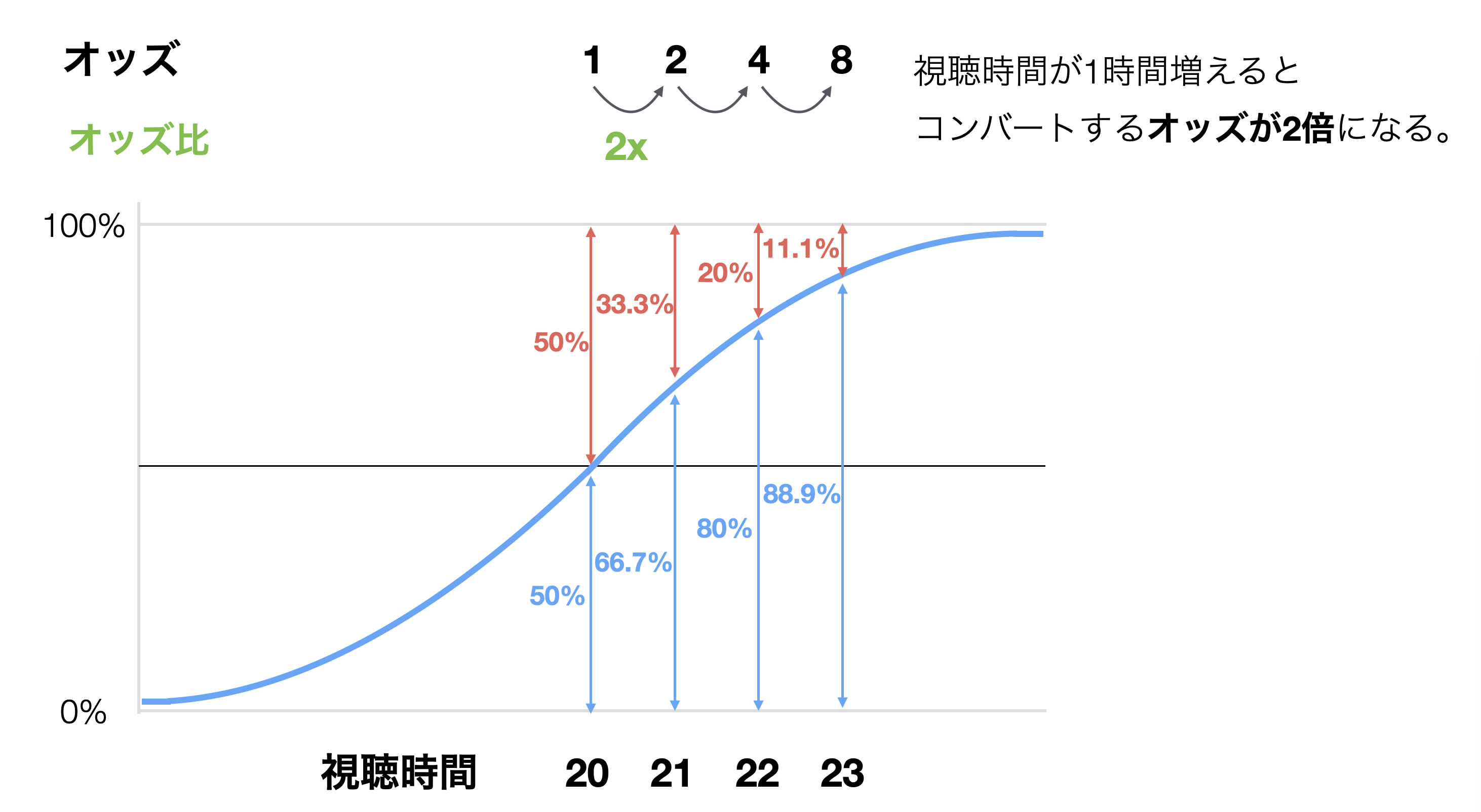
オッズ比とは、予測変数の値が増えた時に、オッズが何倍で増えていくのかを表しています。
下記の例では、視聴時間が増えた時にオッズが2倍ずつで増えているため、オッズ比は「2」となっています。
予測変数がカテゴリー型の時のオッズ比は何を表していますか
予測変数がカテゴリー型の時のオッズ比は、ベースレベルのオッズと比べて、それぞれの値のオッズが何倍であるかを求めています。
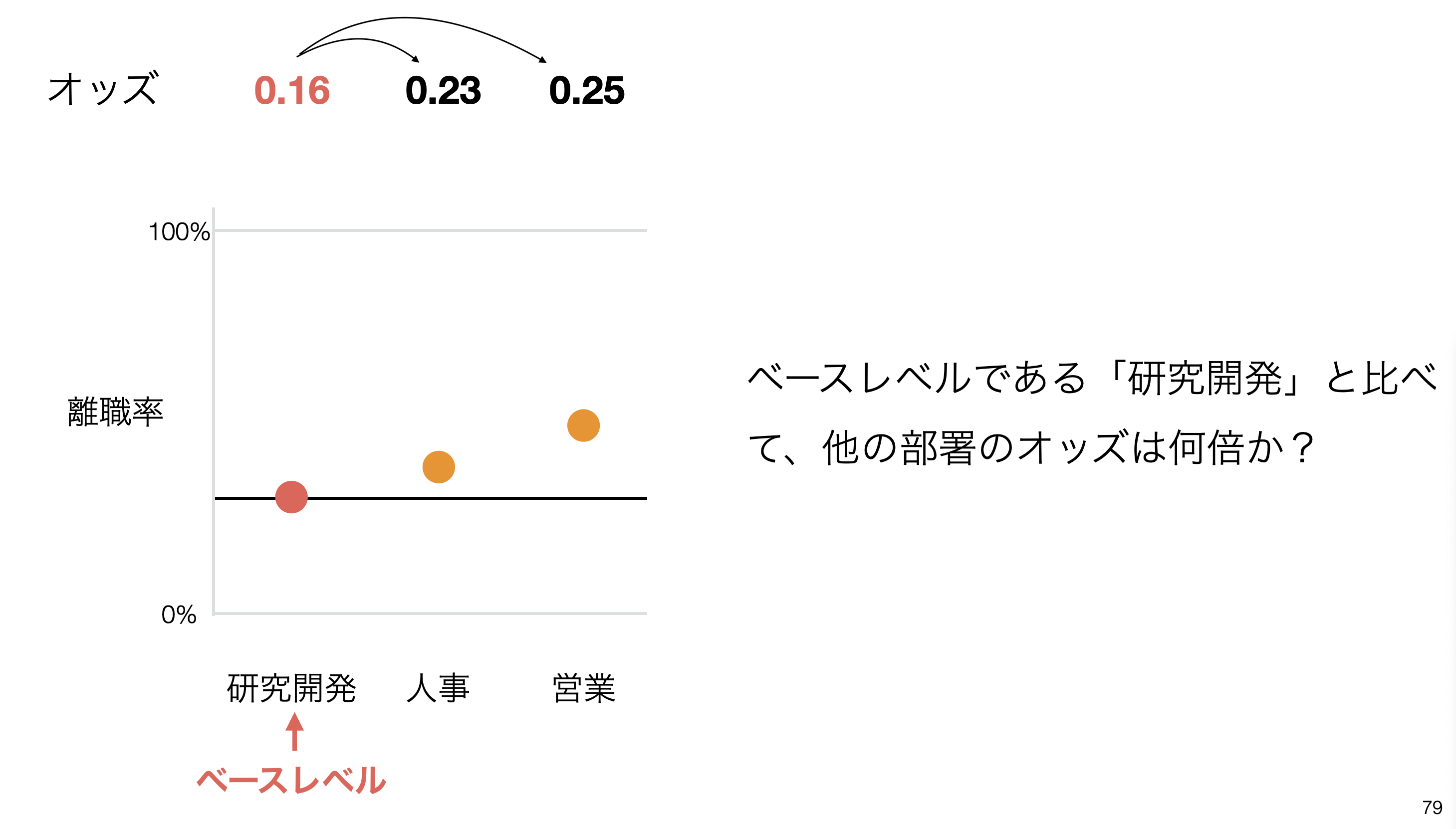 下記の例では、人事では、ベースレベルである研究開発と比べていくことになり、
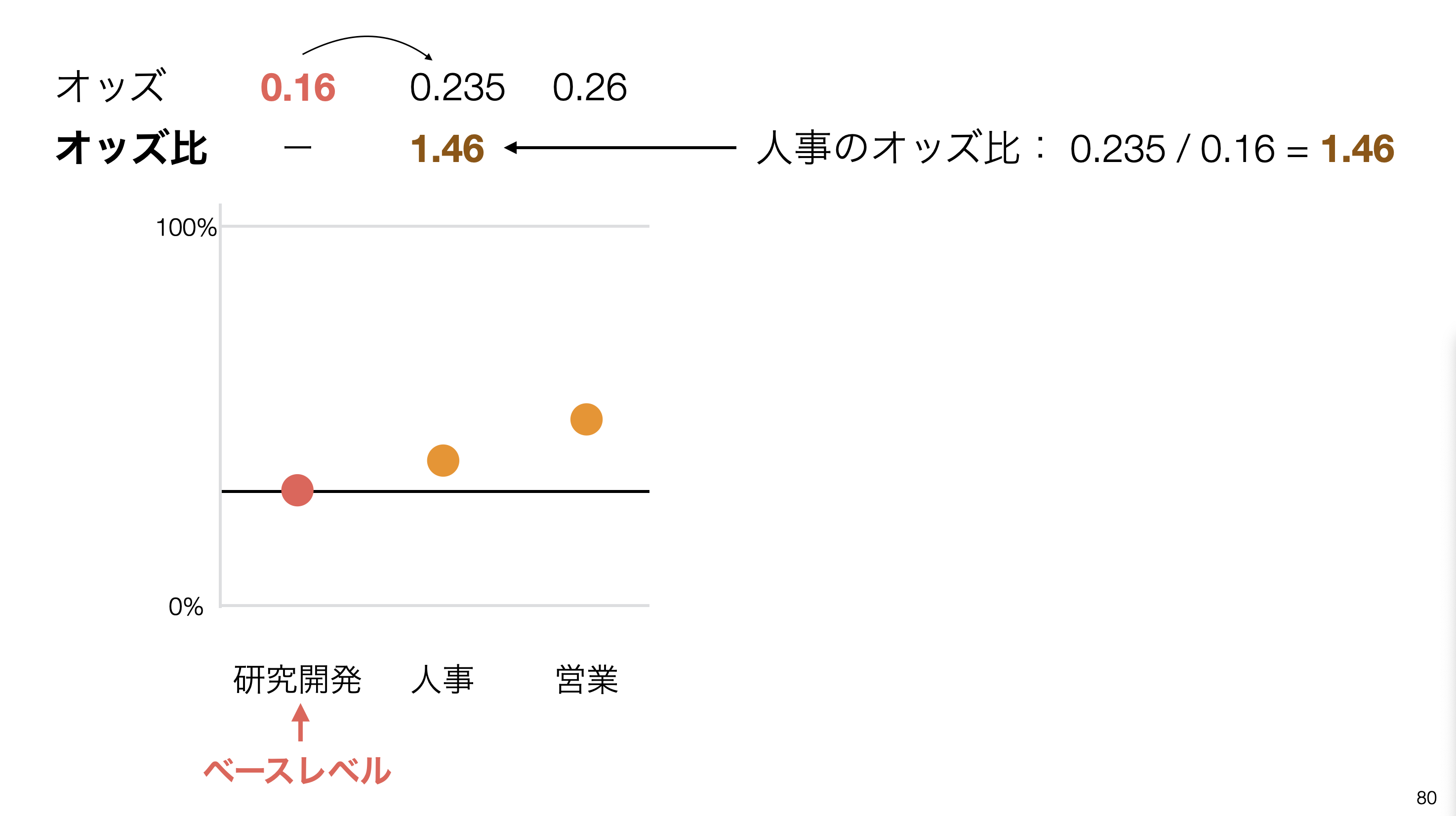
下記の例では、人事では、ベースレベルである研究開発と比べていくことになり、人事のオッズ / 研究開発(ベースレベル)のオッズ)で求めたものが人事のオッズ比になります。
データサイズが少ない時でも、カテゴリー型の予測変数のオッズ比は高く算出されますか
前提として、データサイズが少なかったとしても、TRUEとFALSEの比率が変わらなければ、オッズ自体の値は変わりません。
- 100人いて20人がTRUE、80人がFALSEの時
- 10人いて2人がTRUE、8人がFALSEの時
どちらもオッズとしては同じ0.25になります。
オッズ: 20% / 80% = 0.251つ前の解答でご紹介したカテゴリー型の時のオッズ比の計算を踏まえると、データ数が少なかったとしてもオッズ比自体の計算には、ベースレベルとそれぞれの値のオッズのみが重要になるためデータサイズは考慮されていません。
では、どういった時にカテゴリー型の変数でオッズ比が高くなるのかというと、ベースレベルと比較対象の変数のオッズに差が大きい時にオッズ比が高くなり、差が小さい時にはオッズ比が小さくなるようになっています。
例えば、下記のように研究開発がベースレベルで、人事と営業があった時に、営業の方がオッズが高くなっており、研究開発との差が大きいです。
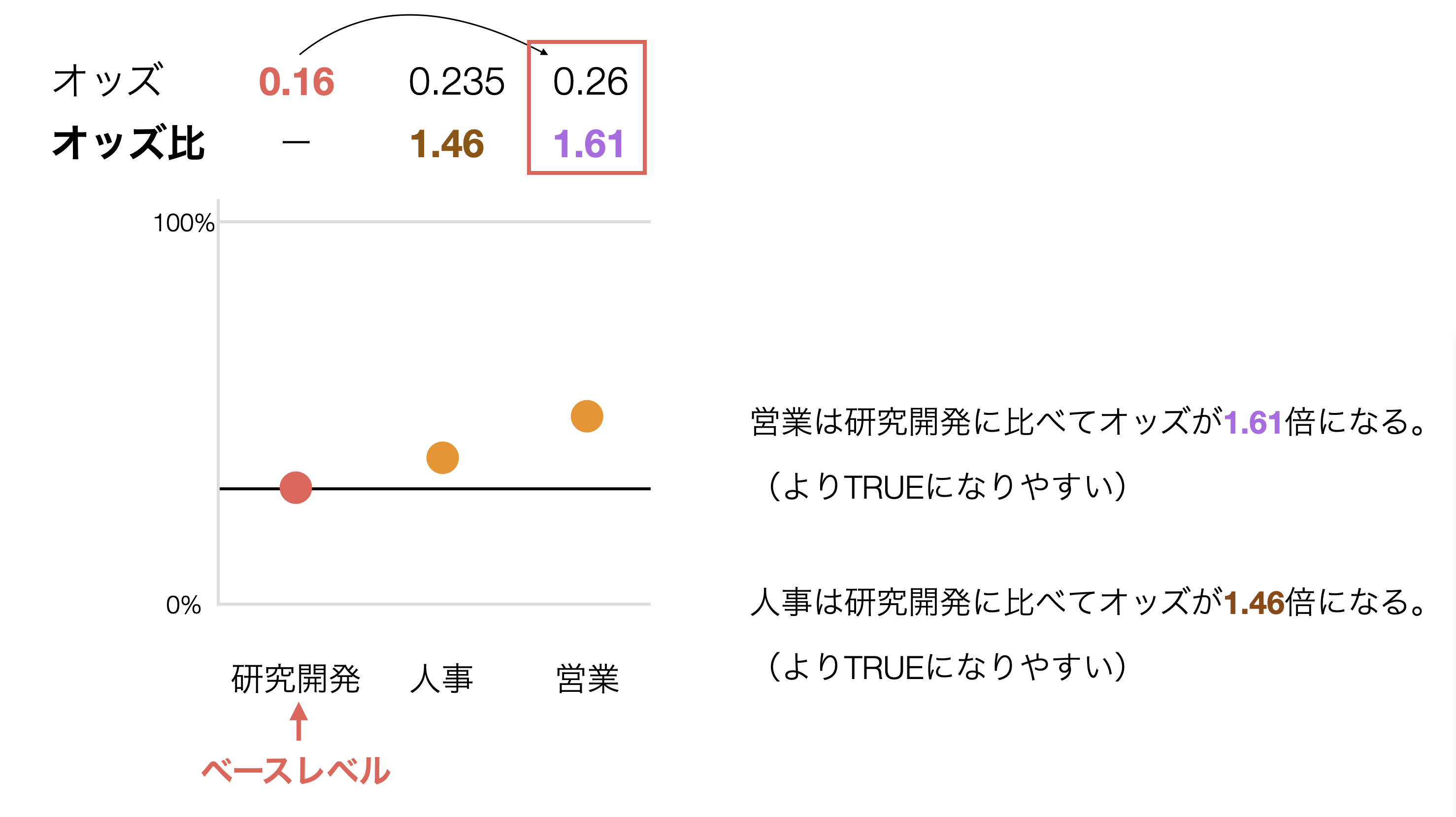
そのため、人事に比べて営業のオッズ比が高くなるという結果になっています。
一方で有意かどうかについては別となり、ロジスティック回帰ではその変数の有意性をオッズ比のP値または信頼区間として表してくれます。
下記の例では、オッズ比は1.46のため、ベースレベルである研究開発に比べて人事は離職するオッズが1.46倍となりますが、信頼区間が0.76 - 2.82と1をまたいでいます。
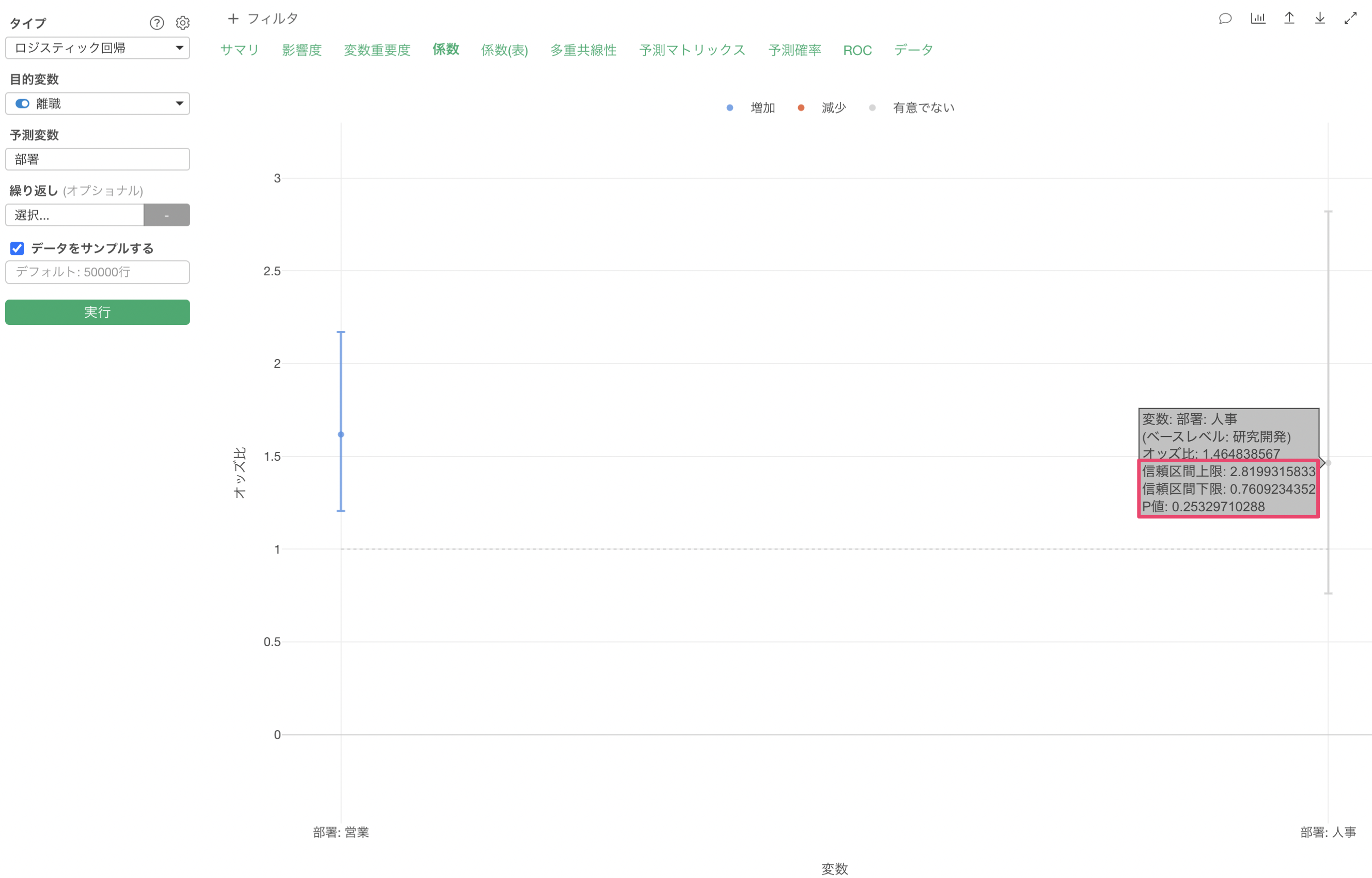
つまりはオッズ比が0.76になるかもしれないし、2.82になるかもしれないことです。オッズ比が1をまたいでいると、オッズが1倍、つまりは研究開発と比べて人事になったとしてもTRUEになる可能性は変わらないという判断になります。
この信頼区間は、データサイズに影響を受け、データサイズが多くなれば信頼区間は短くなり、データサイズが小さければ信頼区間は長くなります。
合わせて、P値の方でも一般的に使用される5%を基準として、有意かどうかを判断していくことが可能です。
Q: 係数タブや係数表タブで表示される係数は標準化回帰係数ですか、それとも、偏回帰係数ですか?
係数タブや係数表タブで表示される係数は予測変数の値を標準化した後の係数(標準化回帰係数)ではなく、「元の単位」における係数(偏回帰係数)となります。
予測変数にあるカテゴリー型の列のベースレベルを変更したい
ロジスティック回帰などの統計のモデルでのカテゴリー型の列を予測変数に選択して実行した際には、ベースレベルと比べて特定の値だった時に有意なのかどうかが分かるようになっており、ベースレベルはその列の値で最頻値(行の数が最も多い)が自動的に選ばれます。
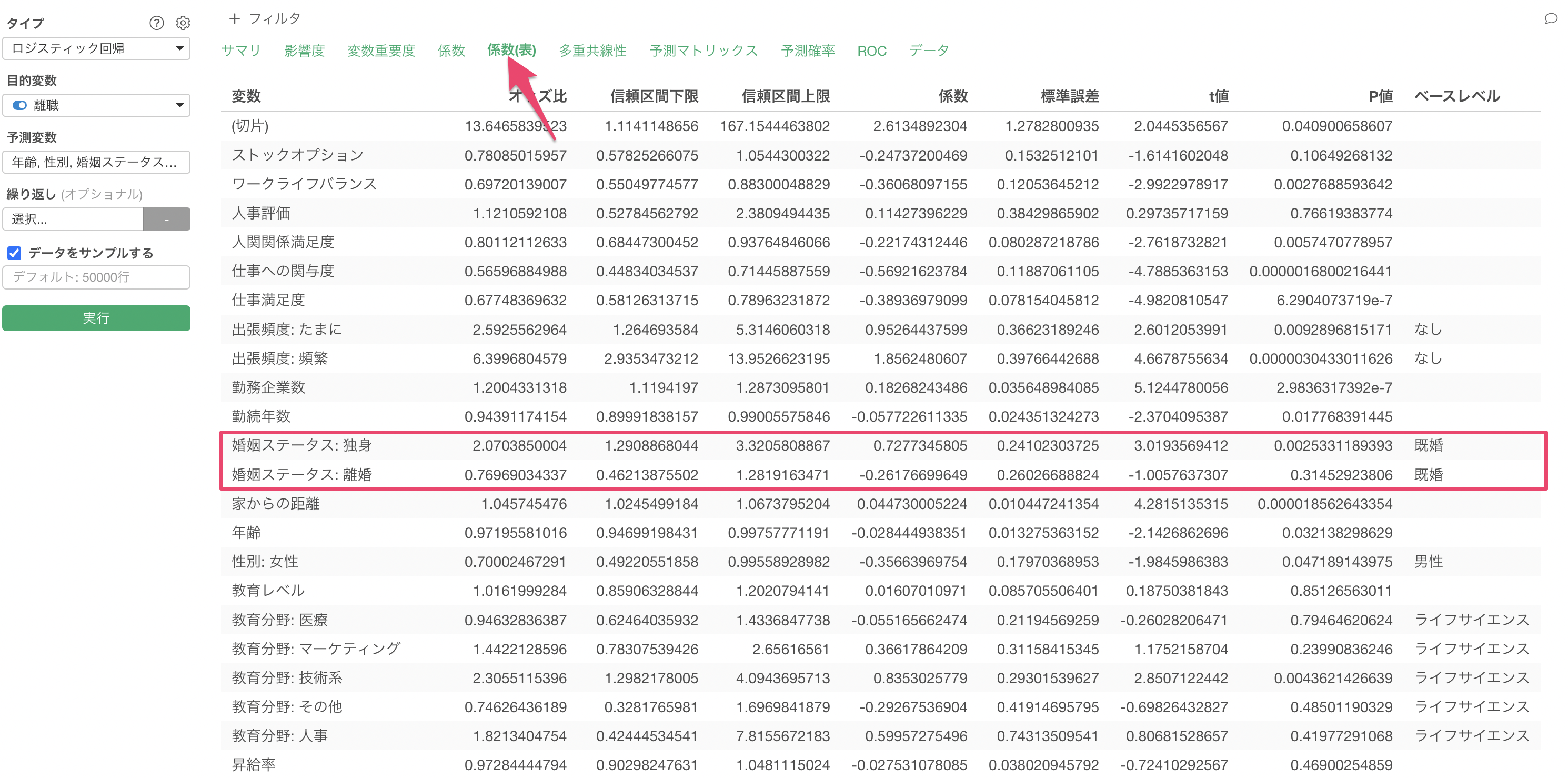
ベースレベルを変更したい場合は、こちらの投稿をご覧ください。
Q: 予測タブで表示されている実測値はどのように求められているのですか?
予測タブの実測値はそれぞれの予測変数のデータタイプによって表示が異なります。 詳しくはこちらのノートをご覧ください。
Q: 予測タブで表示されている予測値はどのように求められているのですか?
予測値のチャートはPartial Dependence Plot(PDP)と呼ばれるもので、注目している変数の値を変化させたときに、予測結果がどう変わるかを可視化したチャートとなります。詳しくはこちらのノートをご覧ください。
Q: 閾値はどのように変更できますか?
プロパティからTRUE/FALSEの境界線に値を指定することで閾値を変更できます。閾値のデフォルトは0.5になっており、0.5以上の場合はTRUEと予測、0.5よりも小さい場合はFALSEと予測されています。
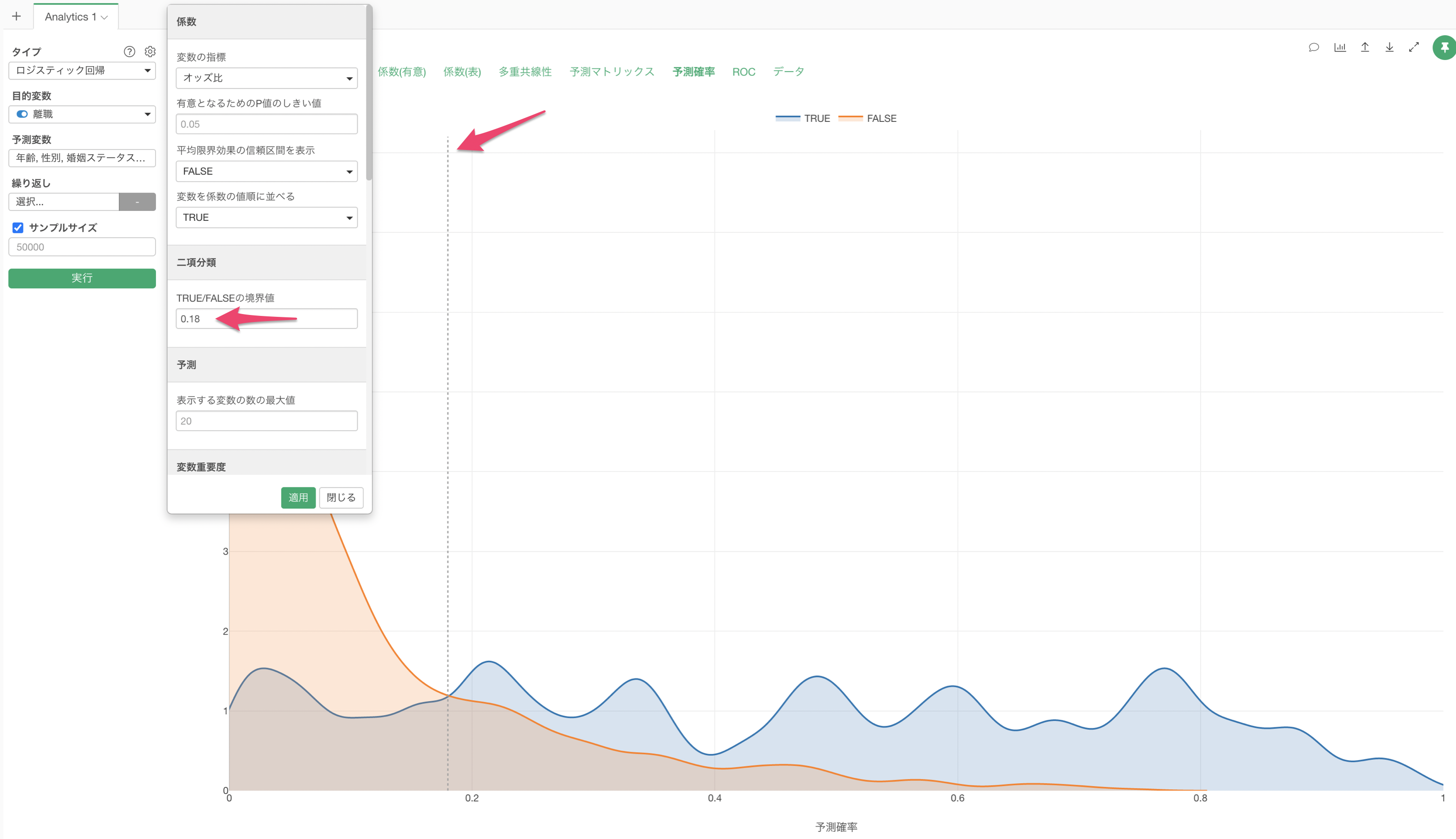
Q: 予測精度を上げるためにしきい値などの調整はどうすれば良いですか。どちらを優先すれば良いですか。
F値を最もよくするしきい値にすることもできますが、ドメインによってどちらを重視したいかは変わります。
Q: タイプ1とタイプ2エラーで、どれくらいなら許せるかの基準値はありますか?
各タイプのエラーが起きたときの損害をどこまで許容できるかによって判断することになります。
Q: 多重共線性タブでVIFが10を超える変数が複数あった時にはどのように予測変数を除いたらいいですか?
VIFが10を超える変数が複数あった時の予測変数の選び方については、こちらの投稿をご参照ください。
Q: 単回帰では有意にならない変数が、重回帰にすると有意になりました。どう解釈すればいいのでしょうか。
単回帰では有意な関係がないと見えていたものが、重回帰にすると有意になることを負の交絡(Negative Confounding)と言います。詳しくはこちらをご覧ください。