サマリ

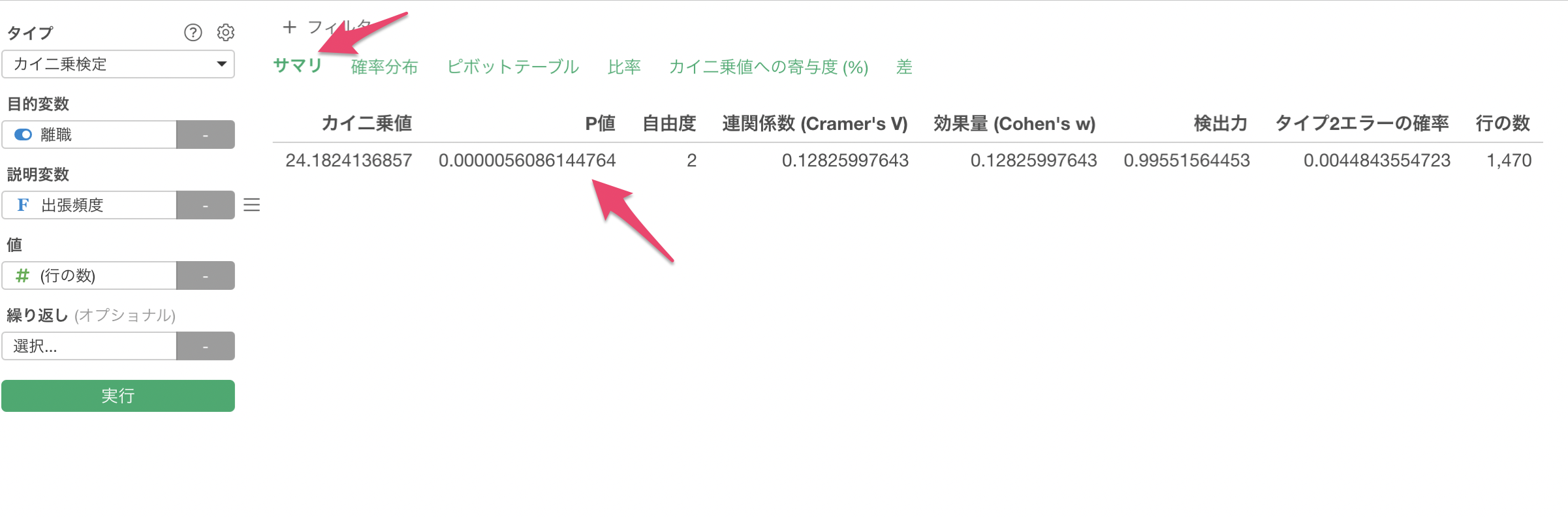
「サマリ」タブでは、検定の結果が有意かどうかを確認できます。2つの変数間に期待値と実測値のずれがないことを前提とした時に、この結果が得られる確率を表すP値から有意かどうか判断ができ、一般的には0.05（5%）を下回ると有意であると言われています。

確率分布

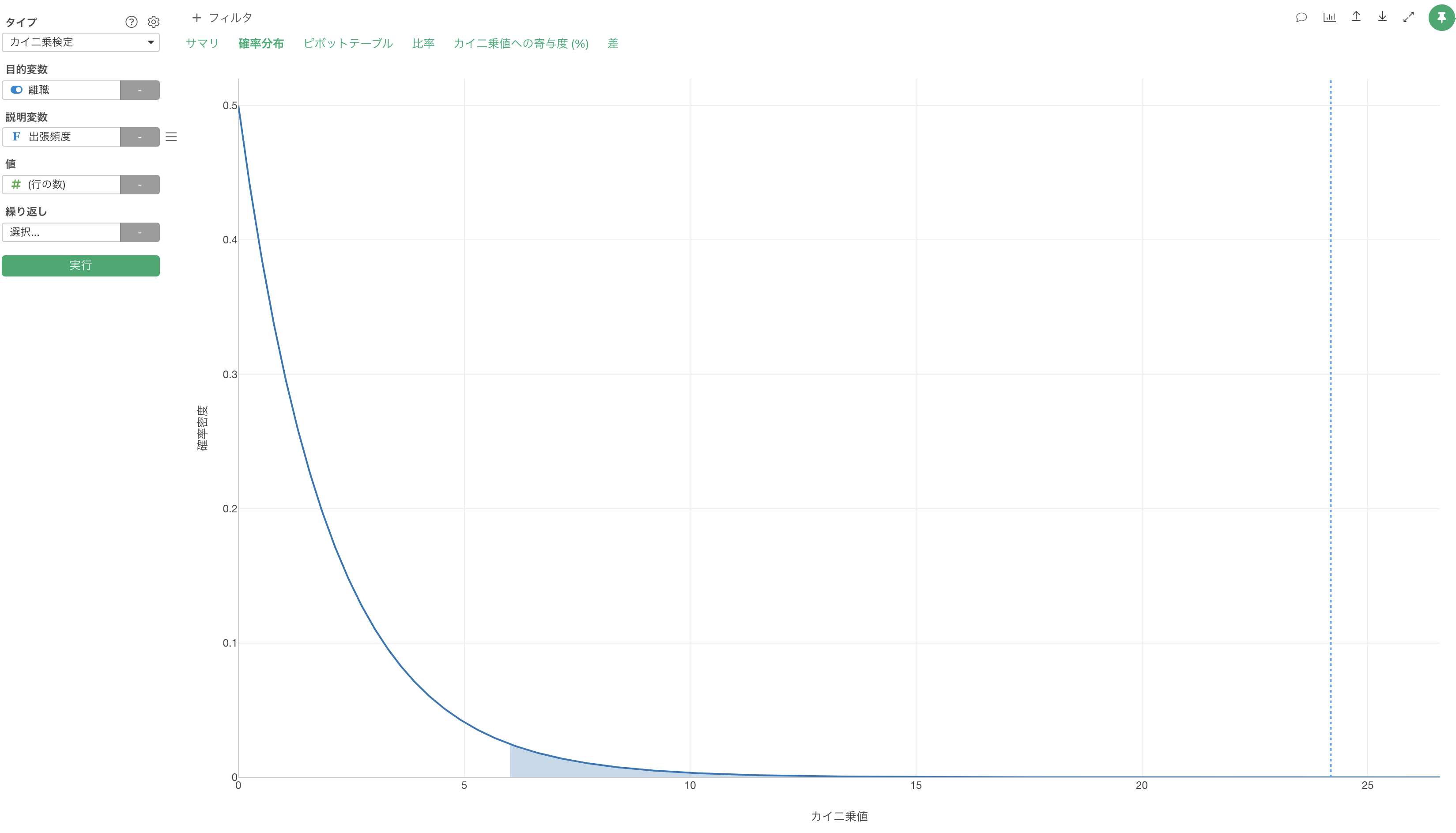
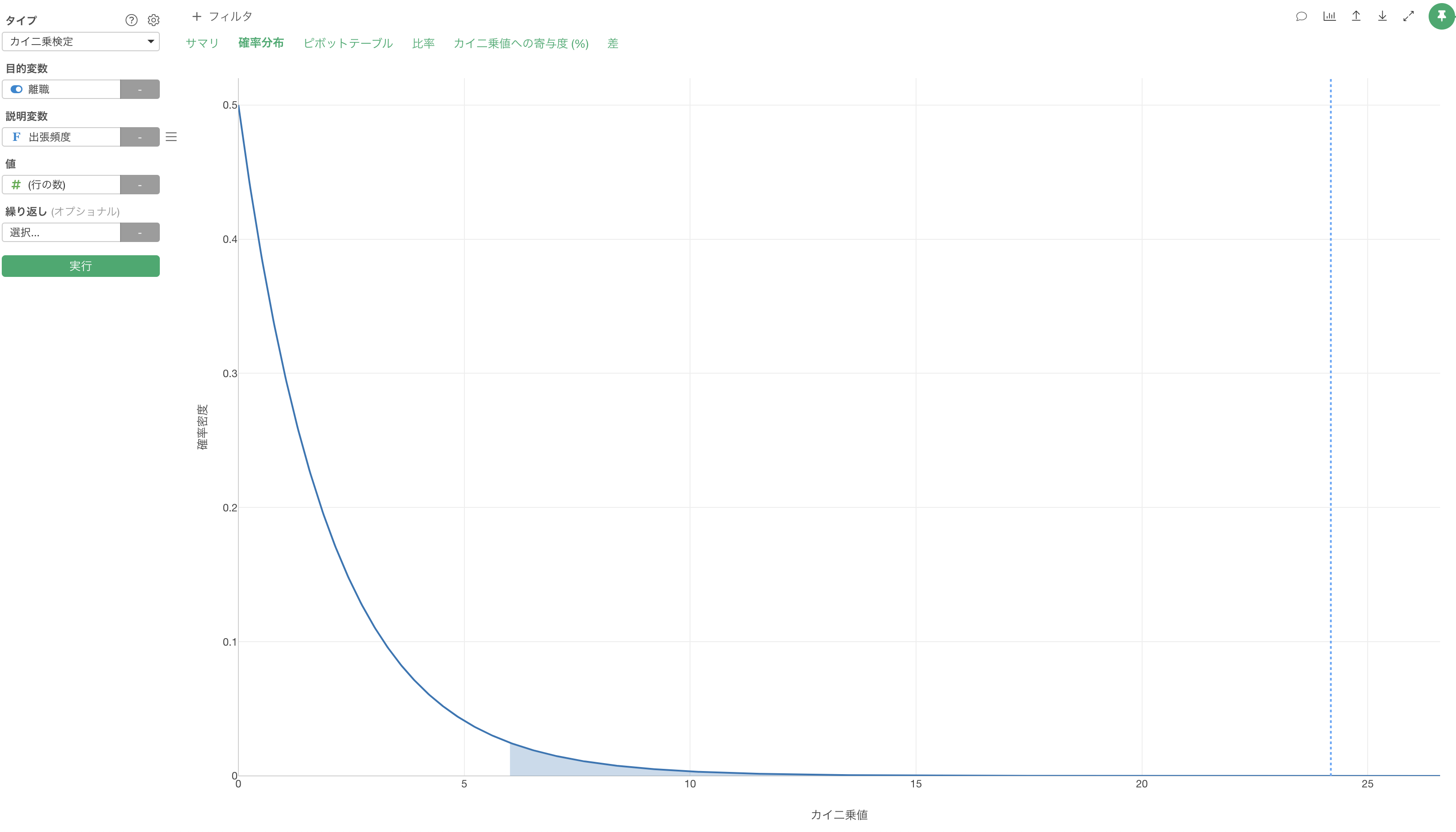
「確率分布」タブでは、使用したデータの自由度を元に、カイ二乗検定で使用する確率分布である「カイ二乗分布」を描き、今回の結果である「カイ二乗値」がカイ二乗分布の中でどの位置にあるのかを点線として表示されます。

比率

「比率」のタブでは、説明変数と目的変数に割り当てたカテゴリーの組み合わせごとに、その中で占める割合がバーチャートとして可視化されます。

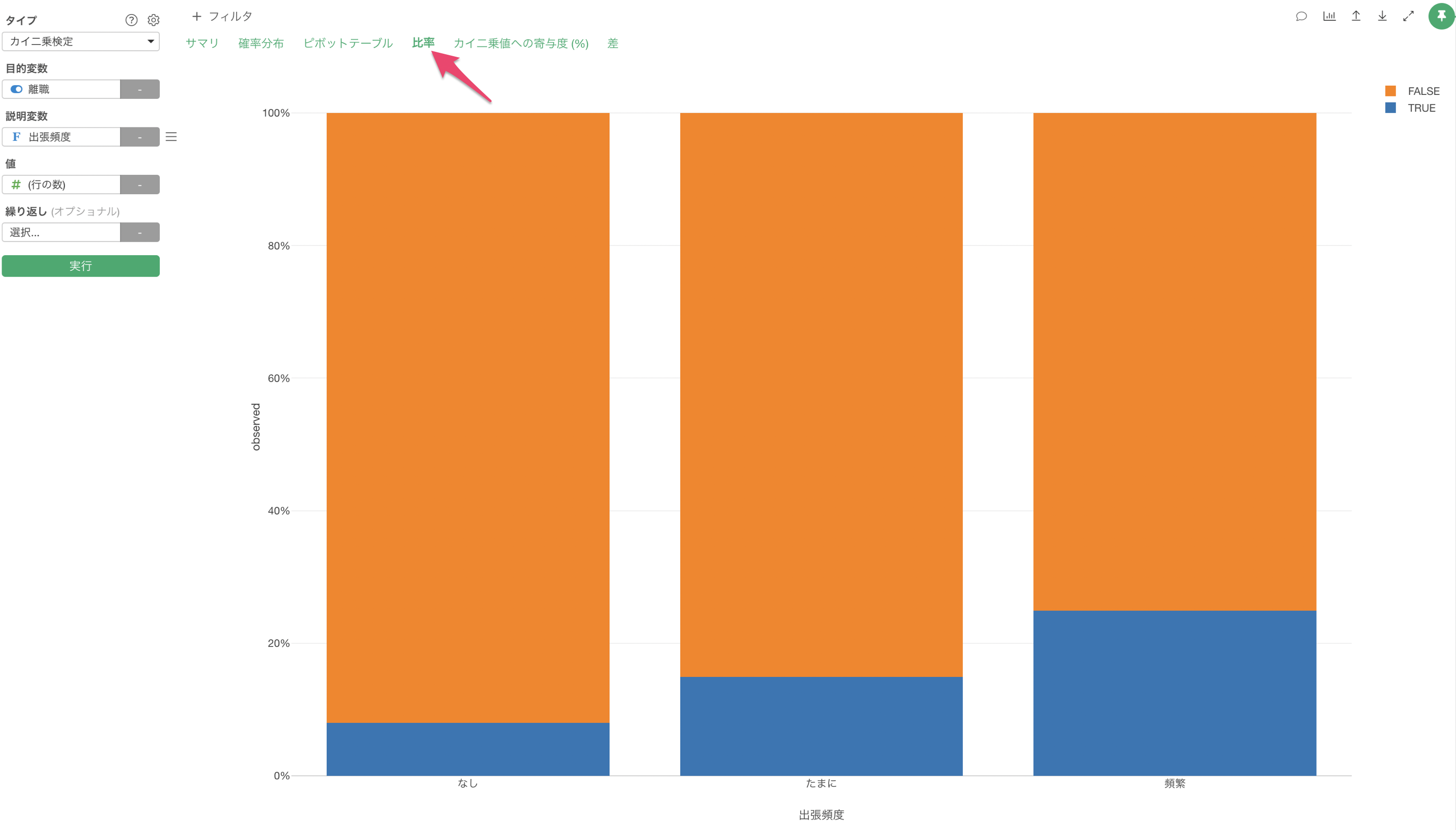
カイ二乗値への寄与度（%）

「寄与度」のタブでは、カイ二乗検定でカイ二乗値に貢献している（期待値と実測値でずれがある）組み合わせを調べることができます。

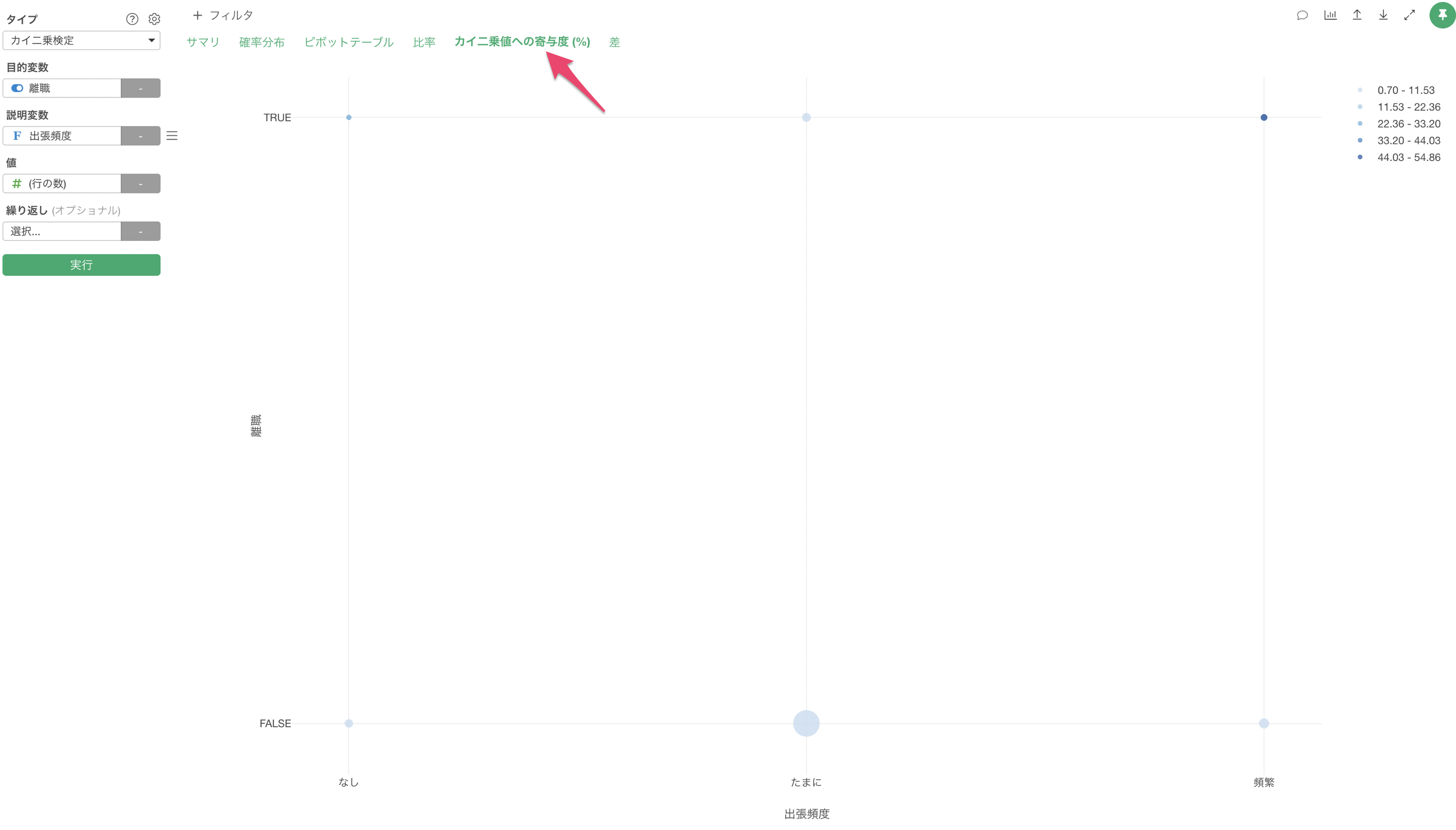
カイ二乗値は実測値と期待値のズレの度合いを表す指標ですが、それぞれの組み合わせのずれが全体のずれ（カイ二乗値）に占める割合（率）を「寄与度」と言います。

下記の例だと最も寄与度が高いのが出張頻度が「頻繁」で離職が「TRUE」の組み合わせで、期待値と実測値のずれのうち「54.86%」がこの組み合わせからきていることがわかります。

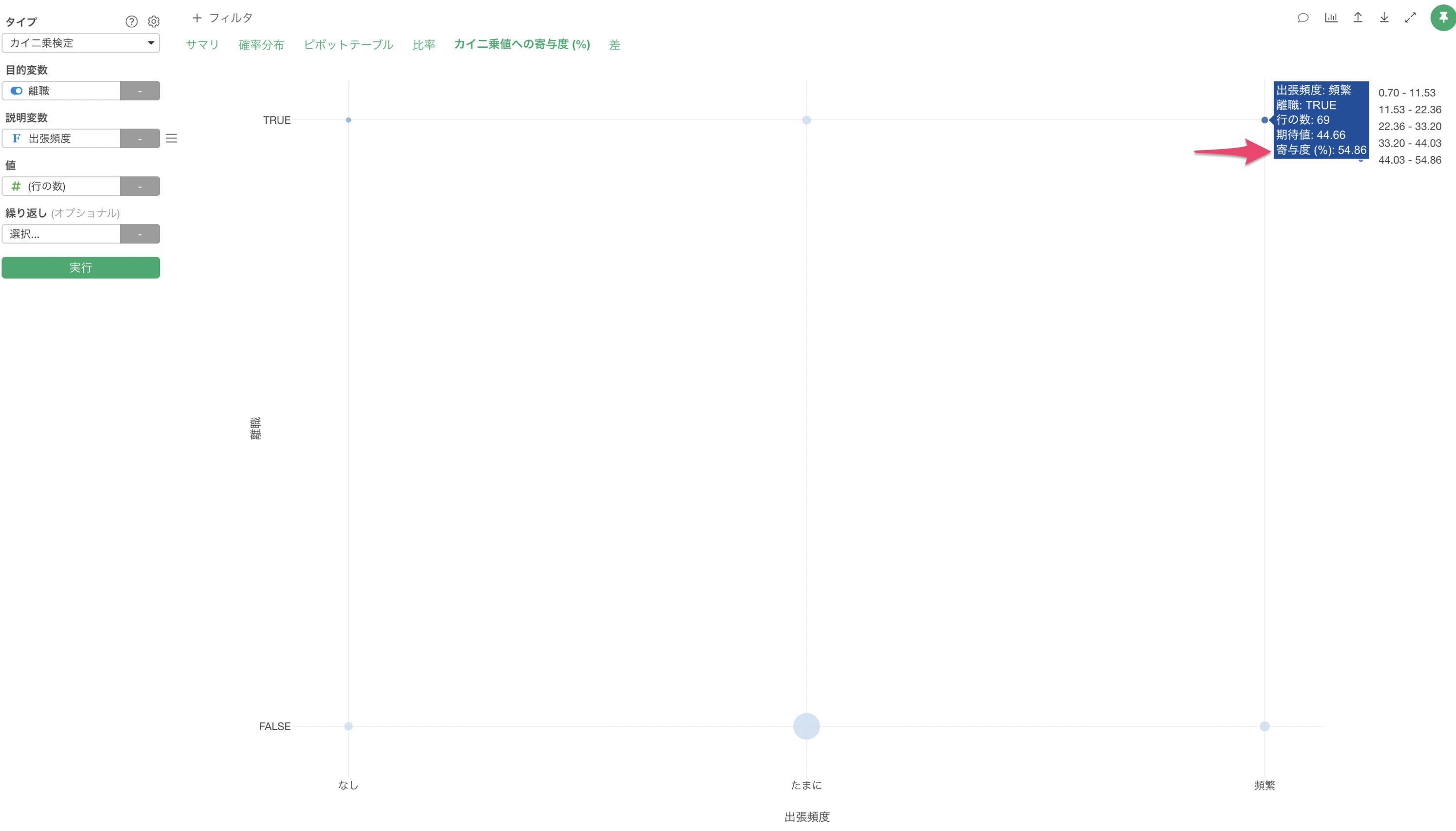
また、円の大きさはその組み合わせにおける行の数を表しており、円のサイズが大きい場合は行の数が多く、小さい場合は行の数が少ないことを表現しています。

差

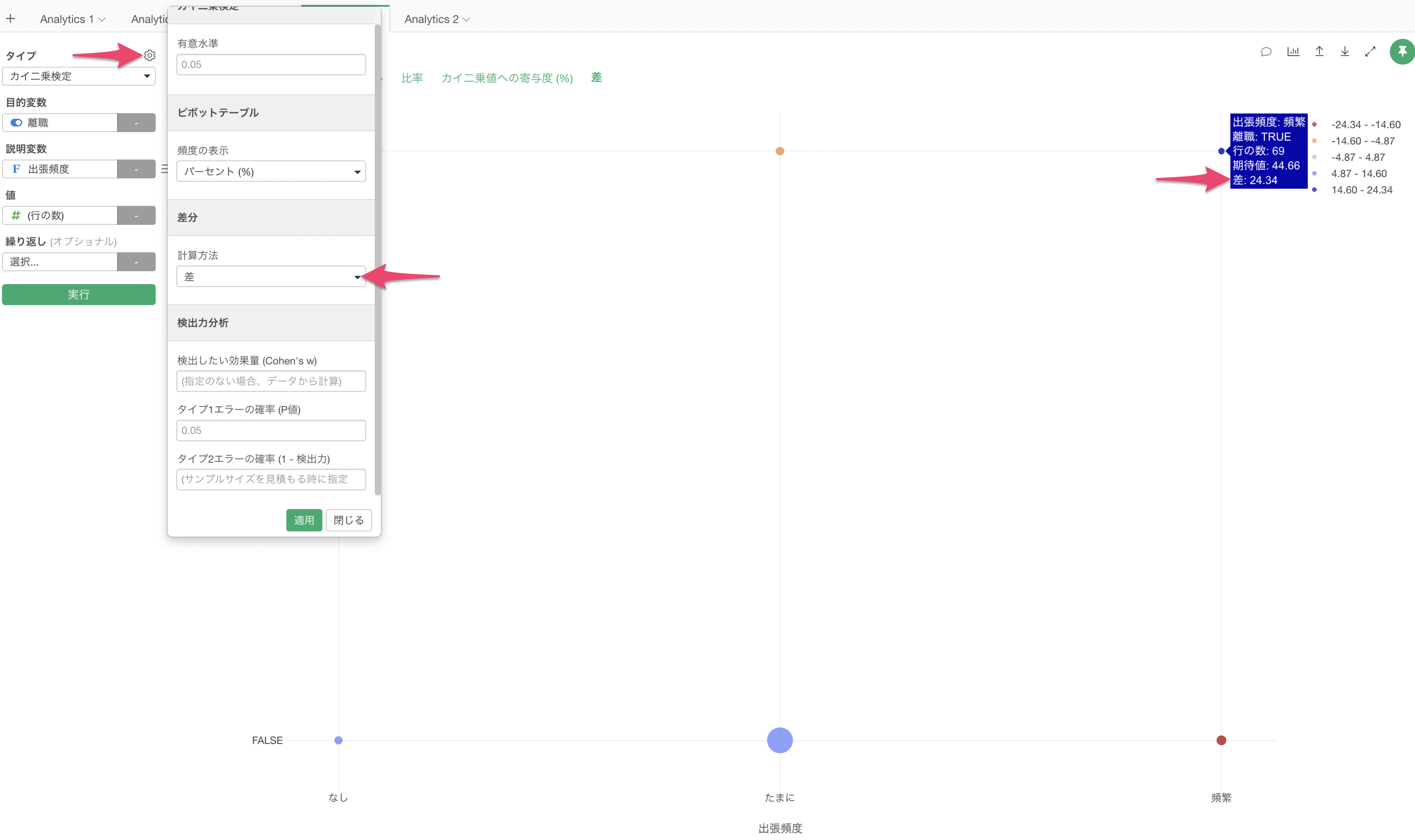
「差」のタブでは、それぞれの組み合わせごとに実測値と期待値のずれを確認することができます。

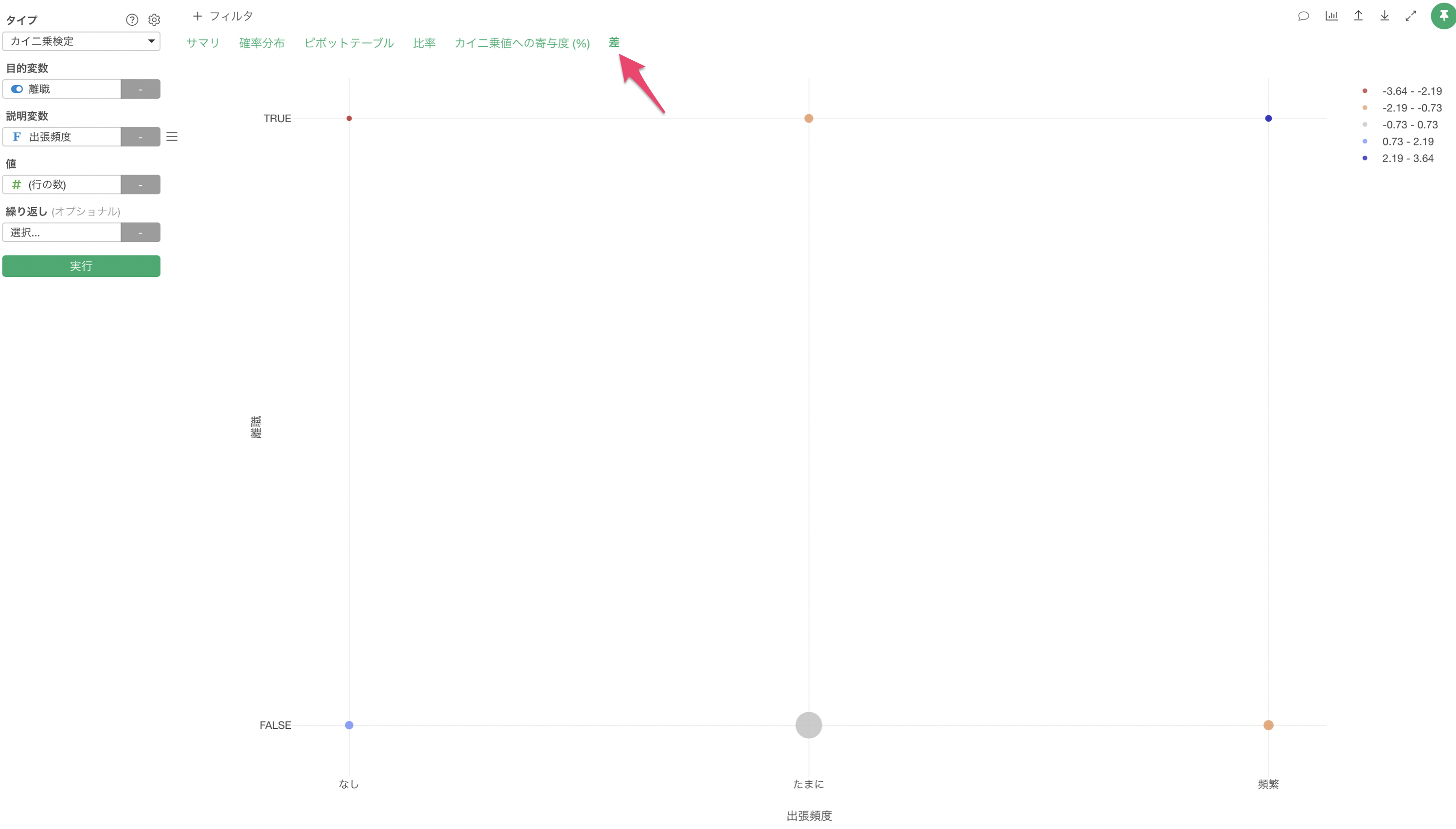
デフォルトでは「標準化された差」が表示されるようになっており、標準化された値が「0」が平均値で偏差値で考えると50となります。もし標準化された差が「2」の場合は偏差値は「70」、「-2」の場合は偏差値は「30」だとして考えることができます。

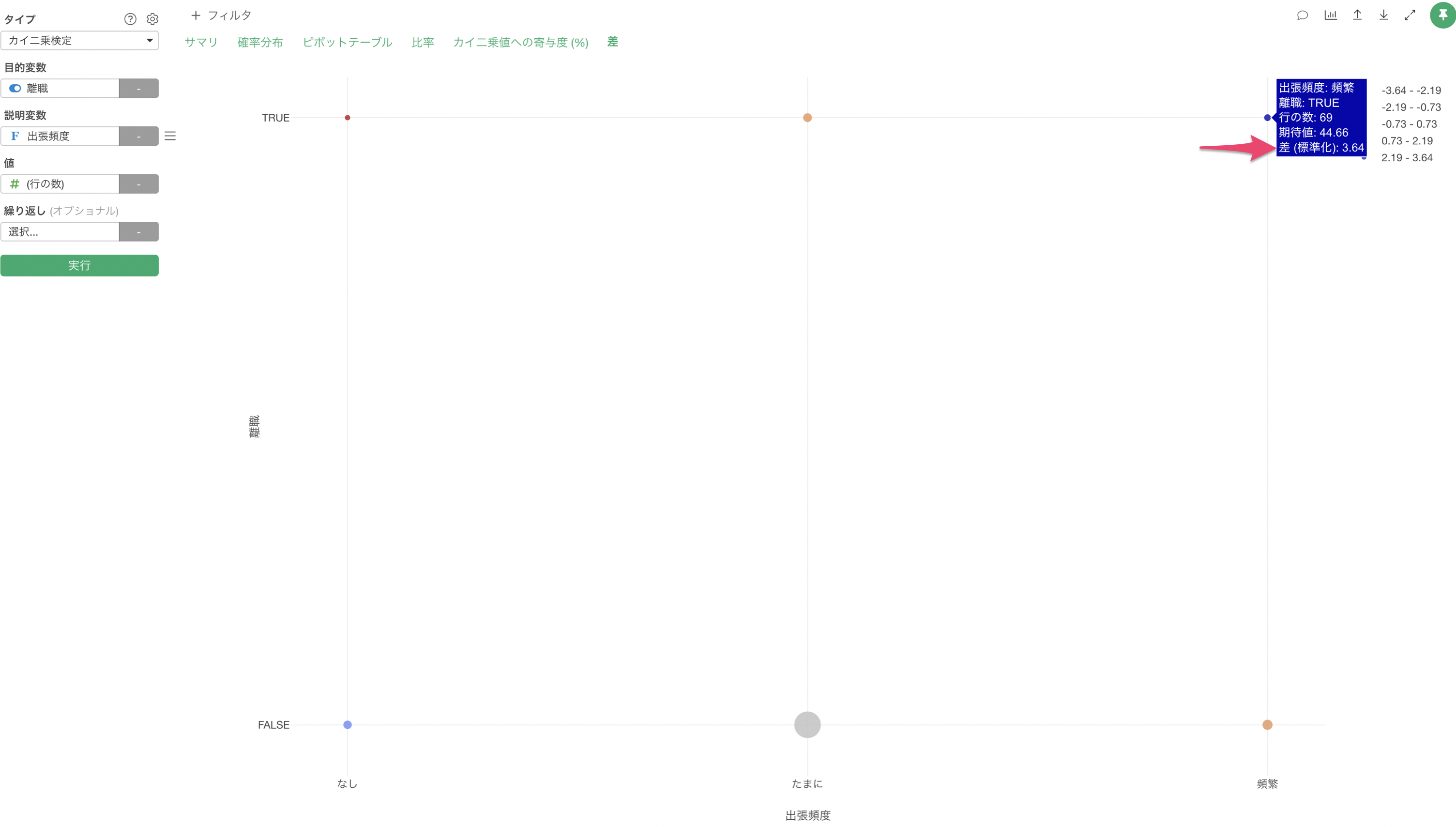
差については、プロパティから計算方法を変更することも可能です。