重回帰とは
重回帰とは、予測変数に複数の変数を選択している「回帰」のモデルを指しています。また重回帰と対比される用語に単回帰があります。単回帰は、予測変数に1つのみの変数を選択している「回帰」のモデルを指しています。
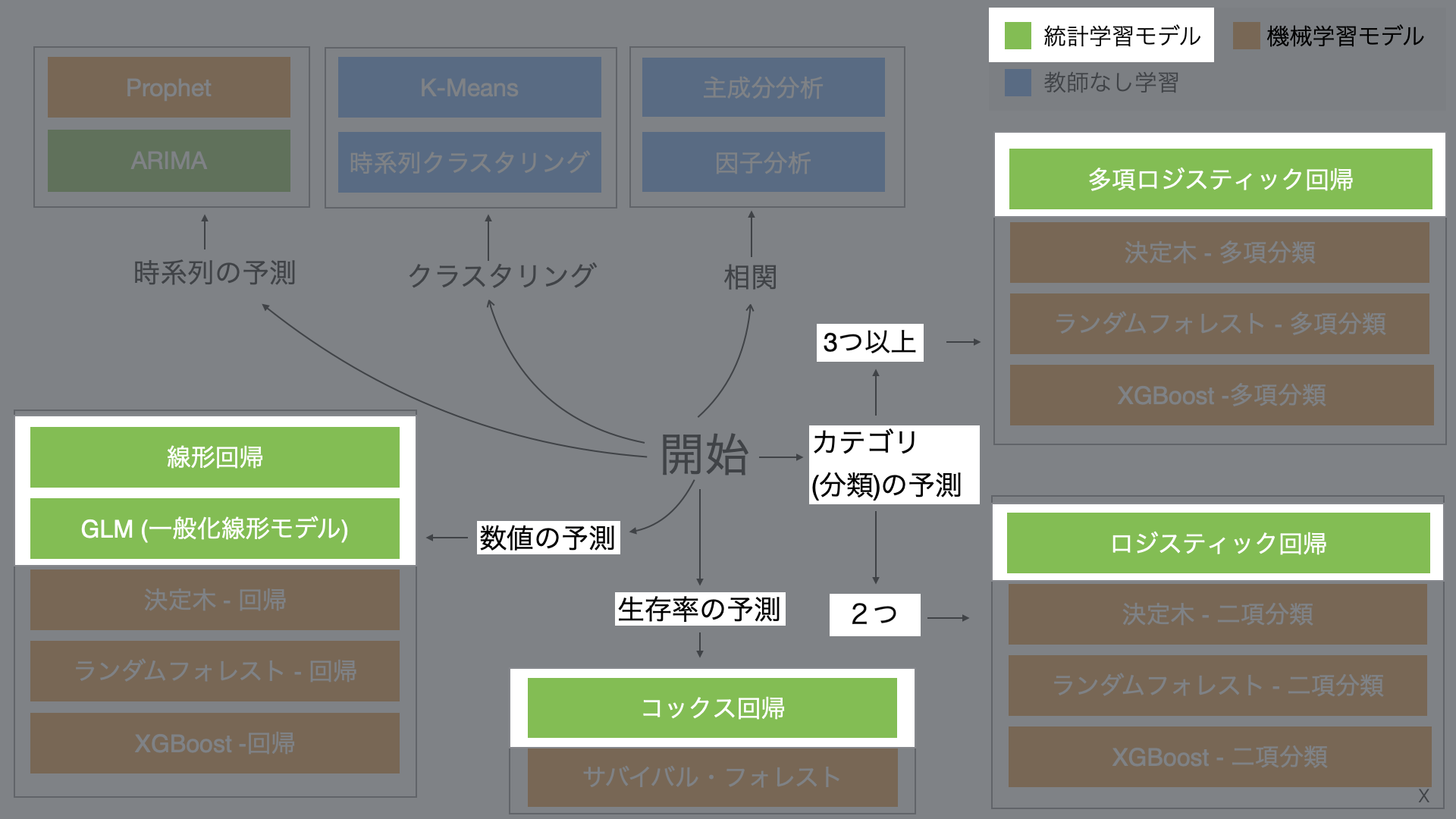
また、回帰には複数のモデル(例: 線形回帰、ロジスティック回帰など)があり、以下のように予測したい目的変数に応じて、利用するモデルを選択いただくことになります。
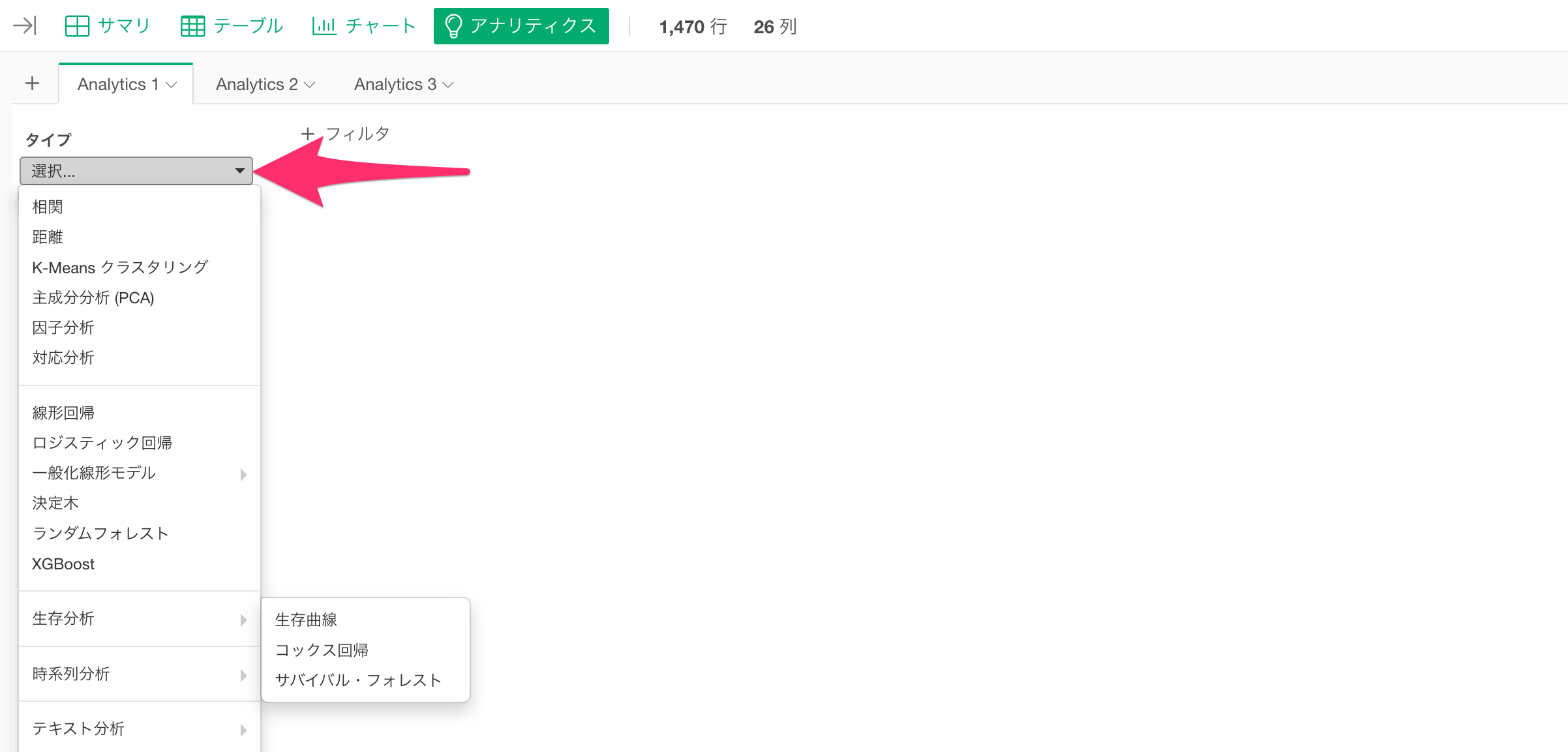
そして、Exploratoryでは、アナリティクスのタイプから回帰のモデルを選択でき、利用可能な回帰のモデルはこちらから確認いただけます。(全てのアナリティクスのタイプには「回帰」という単語がつきます)
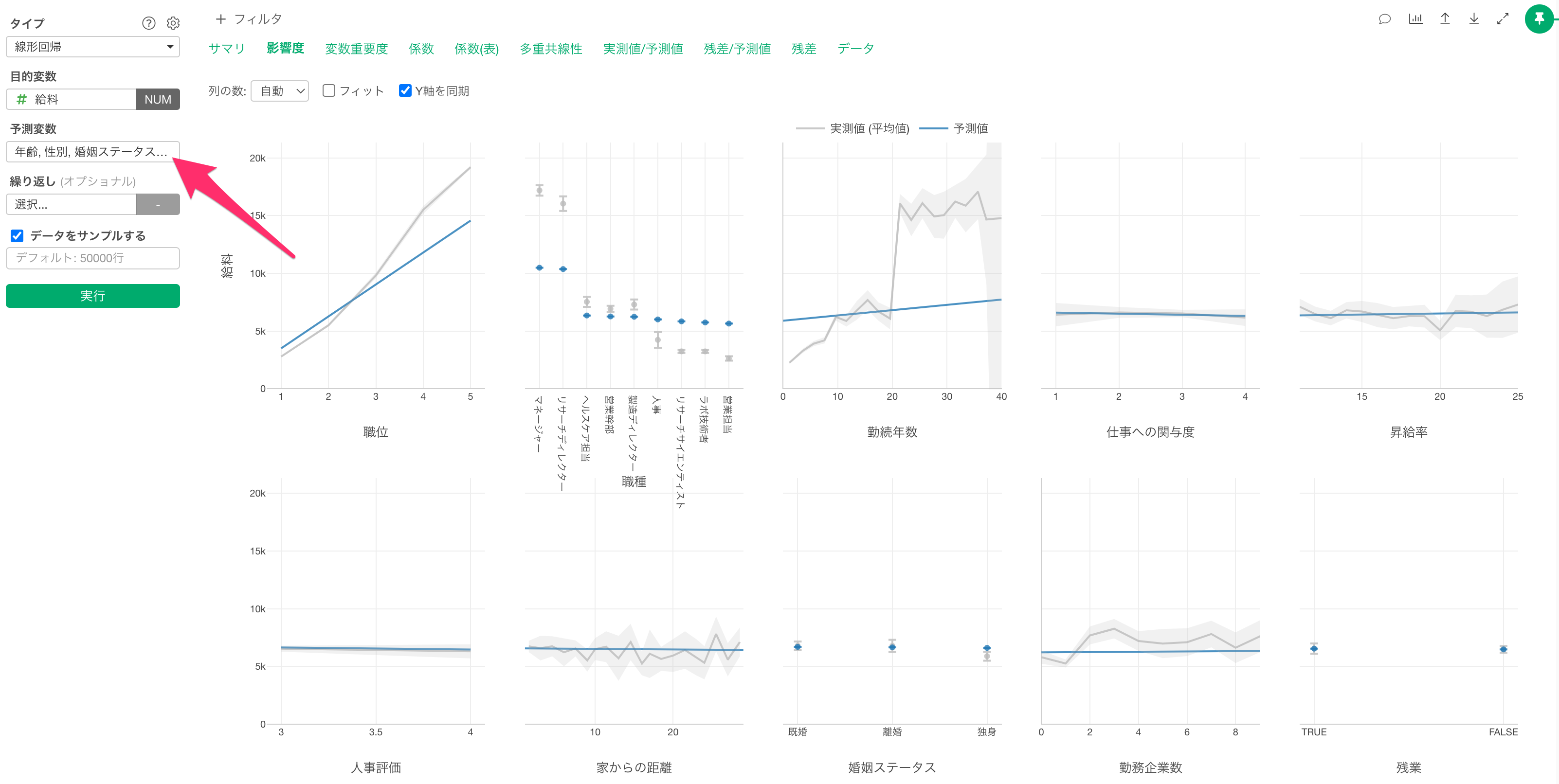
例えば、以下は線形回帰の例ですが、予測変数に1つの変数を選択しているときは、単回帰の線形回帰のモデルを構築していることになり、複数の変数を選択しているときには、重回帰の線形回帰のモデルを構築していることになります。

そのため、上記のモデルは重回帰の線形回帰のモデルと言えます。
なお、重回帰に似た用語に「多変量解析」があります。
多変量解析は、重回帰より幅広い意味で利用されることが多く、複数の変数を同時に分析し、それらの相互関係を明らかにする分析、あるいは、予測の手法の総称となります。そのため、重回帰は多変量解析のアプローチの1つと言えます。