一般化線形モデル - GLM - 正規分布の使い方
一般化線形モデル(GLM)の中でも正規分布を用いるモデルは、実質的には線形回帰モデルと同じ役割を果たします。GLM - 正規分布は、目的変数が正規分布に従い、恒等リンク関数を使用する場合、線形回帰と同じパラメータ推定値を得ることになります。
しかし、GLMと線形回帰では推定方法が異なります。線形回帰が最小二乗法を用いるのに対し、GLMは最尤推定法を使用します。この違いにより、GLMは線形回帰の発展形として、より柔軟なモデリングの基盤となっています。例えば、後に目的変数の分布を二項分布やポアソン分布に変更する可能性がある場合、最初から同じGLMの枠組みで分析できる利点があります。
また、正規分布GLMでは、リンク関数を変更することで、より複雑な関係性のモデル化が可能です。例えば、対数リンクを使用することで、乗法的な関係をモデル化できます。これは、線形回帰では変数変換を行わなければならない場合でも、GLMではリンク関数の選択で対応できることを意味します。
1. どういった時に使えるのか
GLM(正規分布)は、データ分析における重要な選択肢として、いくつかの特徴的な場面で強みを発揮します。異なる確率分布での分析を将来的に検討している場合、GLMの枠組みを採用することで、分析の一貫性を保ちつつ、柔軟な拡張が可能となります。例えば、最初は正規分布で分析を始め、後にデータの特性に応じてポアソン分布や二項分布への移行が必要になった場合でも、同じGLMの枠組みの中で対応できます。
また、リンク関数の変更による非線形関係性の表現も、GLMの重要な特徴です。売上金額と説明変数の関係が単純な線形関係ではなく、対数的な関係にある場合、GLMでは対数リンク関数を選択することで直接的にモデル化が可能です。最尤推定法を用いる点も特徴的で、この推定方法により統計的により厳密な推論が可能となり、特に大規模なデータセットや複雑な関係性を持つデータの分析において、より信頼性の高い結果を得ることができます。
一方、データの関係性が明確に線形である場合や、単純な線形関係のみを仮定する場合は、通常の線形回帰で十分かもしれません。線形回帰は最小二乗法を用いるため、パラメータの解釈がより直感的であり、特に説明変数と目的変数の関係が明確に線形である場合には、余分な複雑さを避けることができます。このように、GLM(正規分布)と線形回帰の選択は、データの特性や分析の目的、結果の活用方法によって判断する必要があります。
代表的なデータ例としては以下のようなものが挙げられます:
- ECサイトの購入金額データ(顧客属性、閲覧履歴、購入履歴など)
- 従業員の給与データ(基本情報、業績評価、スキル指標など)
- 不動産の販売価格データ(物件情報、立地条件、市場動向など)
- スポーツ選手のパフォーマンスデータ(基礎能力、コンディション、試合実績など)
2. ユースケース
EC事業での使い方
- ECサイトでは、顧客の購入金額に影響を与える要因を分析する際に使用できます。
- 具体的には、サイト訪問回数、商品閲覧数、会員ランクなどの要因が購入金額にどの程度影響を与えているかを分析することで、重要な要因を特定できます。
- これにより、優先的に改善すべき施策(例:商品閲覧を促進するUI改善、会員ランク制度の見直し)を決定できます。
人事部門での使い方
- 従業員の評価スコアに影響を与える要因を分析する際に活用できます。
- 具体的には、研修受講回数、プロジェクト参加数、勤続年数などの要因が評価スコアにどの程度影響を与えているかを分析できます。
- これにより、人材育成施策の優先順位付けや評価制度の改善に活用できます。
マーケティング担当者での使い方
- 顧客の購買単価に影響を与える要因を分析する場面で使用できます。
- 具体的には、広告接触回数、メルマガ開封率、SNSフォロー状況などの要因分析が可能です。
- これにより、効果的なマーケティング施策の立案やROIの改善に活用できます。
品質管理担当者での使い方
- 製品品質スコアに影響する製造条件の分析に活用できます。
- 具体的には、温度、圧力、原材料配合比などの要因が品質スコアに与える影響を分析できます。
- これにより、品質向上のための製造条件の最適化や重点管理項目の特定が可能です。
3. Exploratoryで一般化線形モデル - GLM - 正規分布を実行する
使用するデータ
今回は「ECサイト売上データ」を使用します。データはこちらからダウンロードが可能となっています。
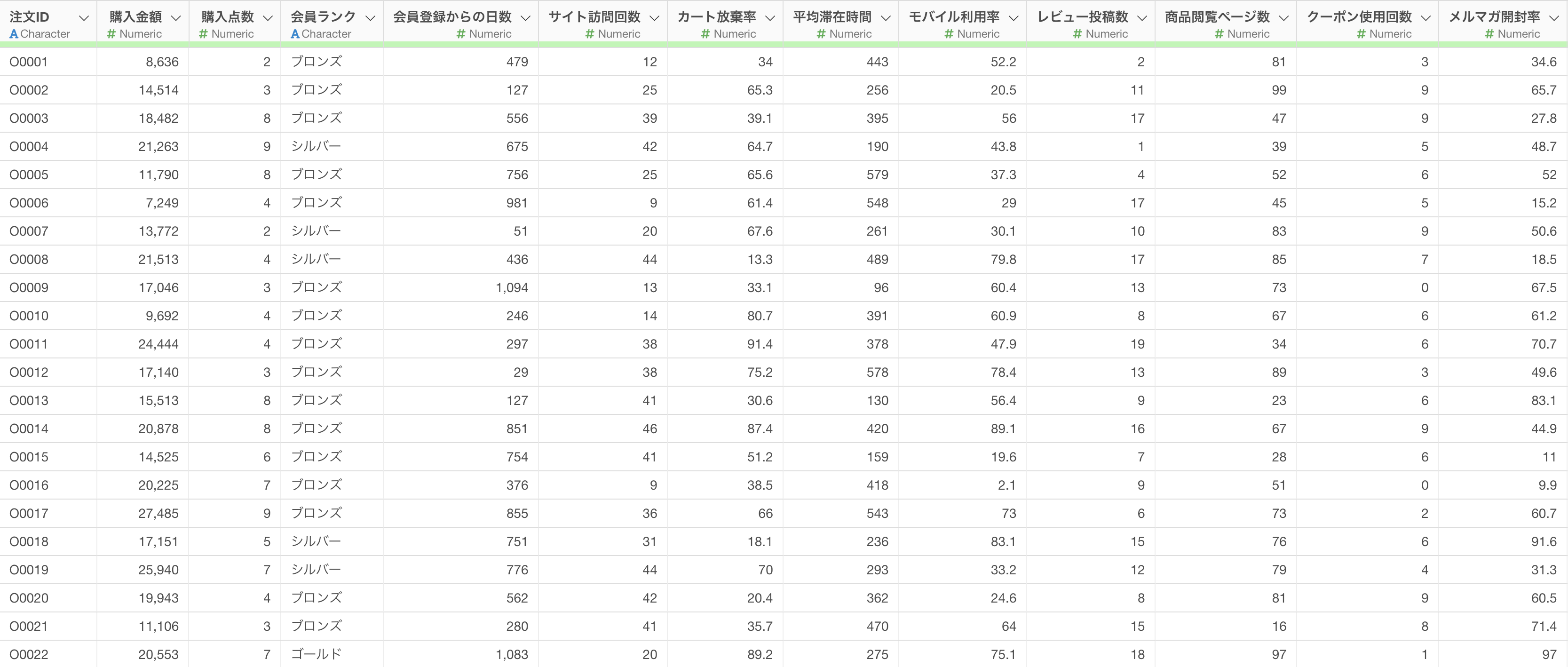
このデータは1行が1回の注文を表し、購入金額を目的変数として、購入点数、会員ランク、サイト訪問回数などの顧客行動データが含まれています。
GLM(正規分布)を実行するためには、以下のようなデータ構造が必要となります:
- 目的変数は連続値であること
- 説明変数は数値型またはカテゴリ型であること
- 欠損値が含まれていないこと
- 極端な外れ値が処理されていること
アナリティクスを作成する
ECサイト売上データから「アナリティクス・ビュー」を開きます。
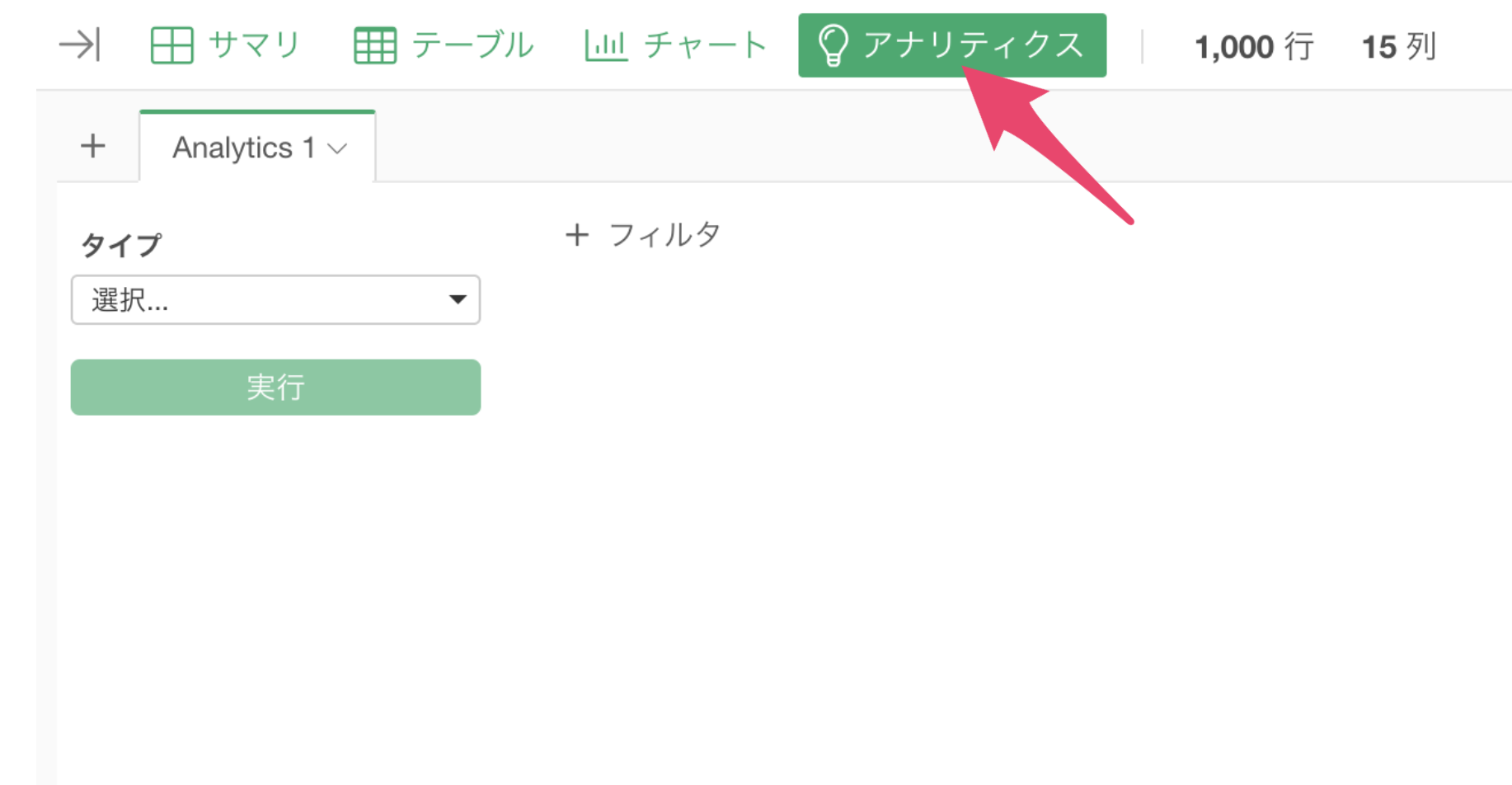
タイプに「一般化線形モデル」を選び、「GLM - 正規分布」を選択します。
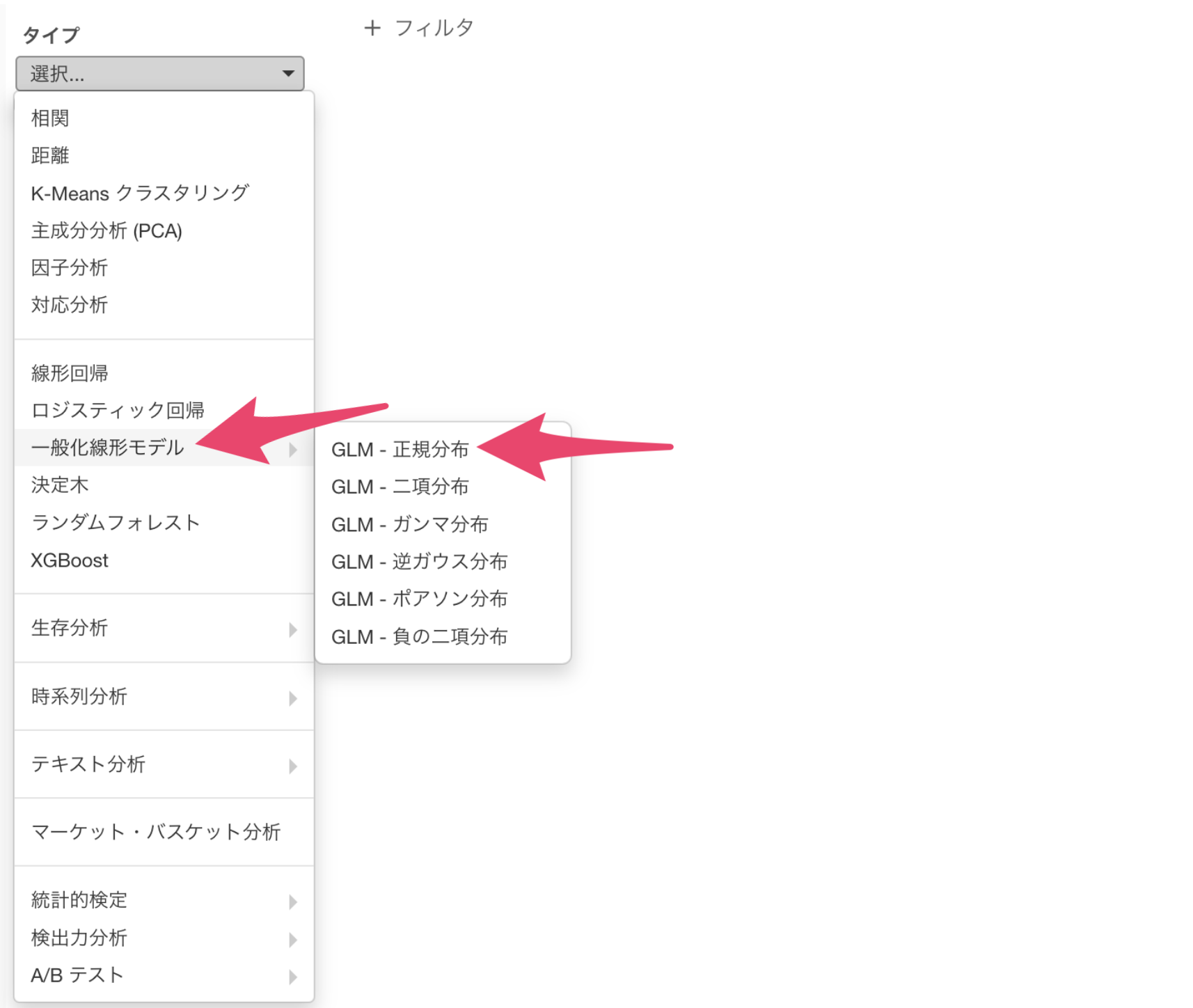
目的変数には「購入金額」の列を割り当てます。
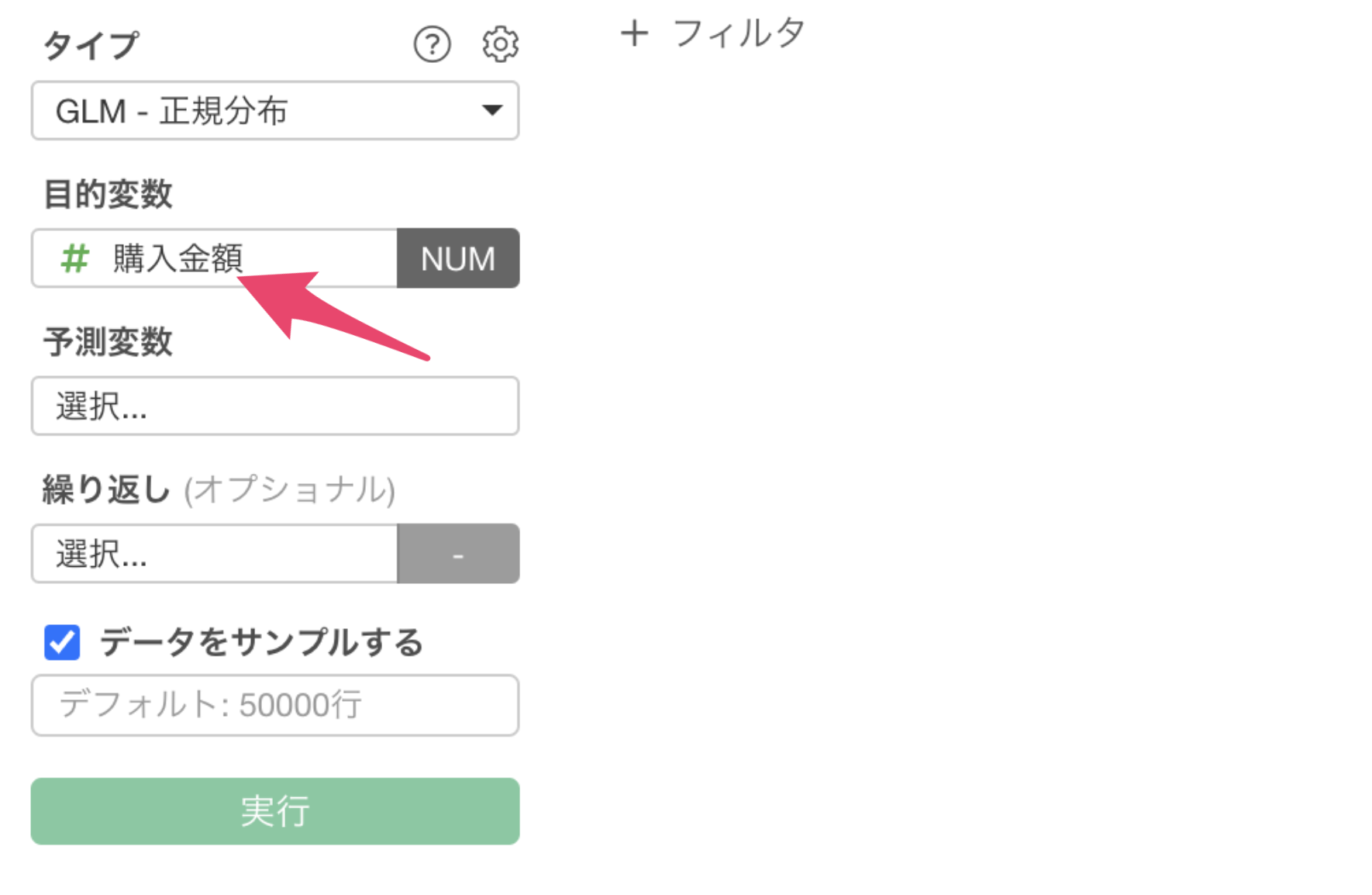
予測変数には、「購入点数」から「商品カテゴリ数」までの列を選択して割り当てます。
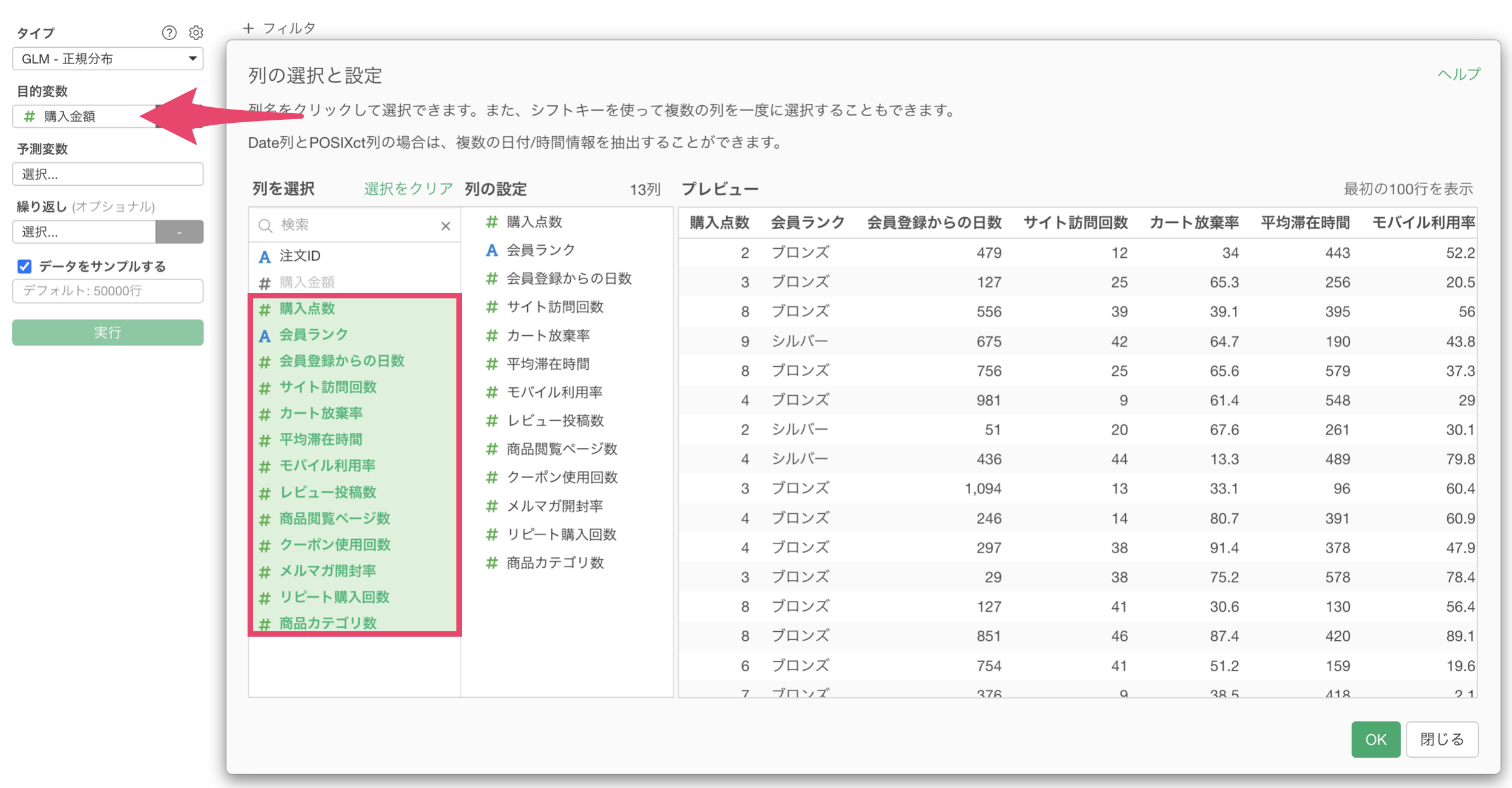
最後に、「実行」ボタンをクリックして実行結果を確認します。
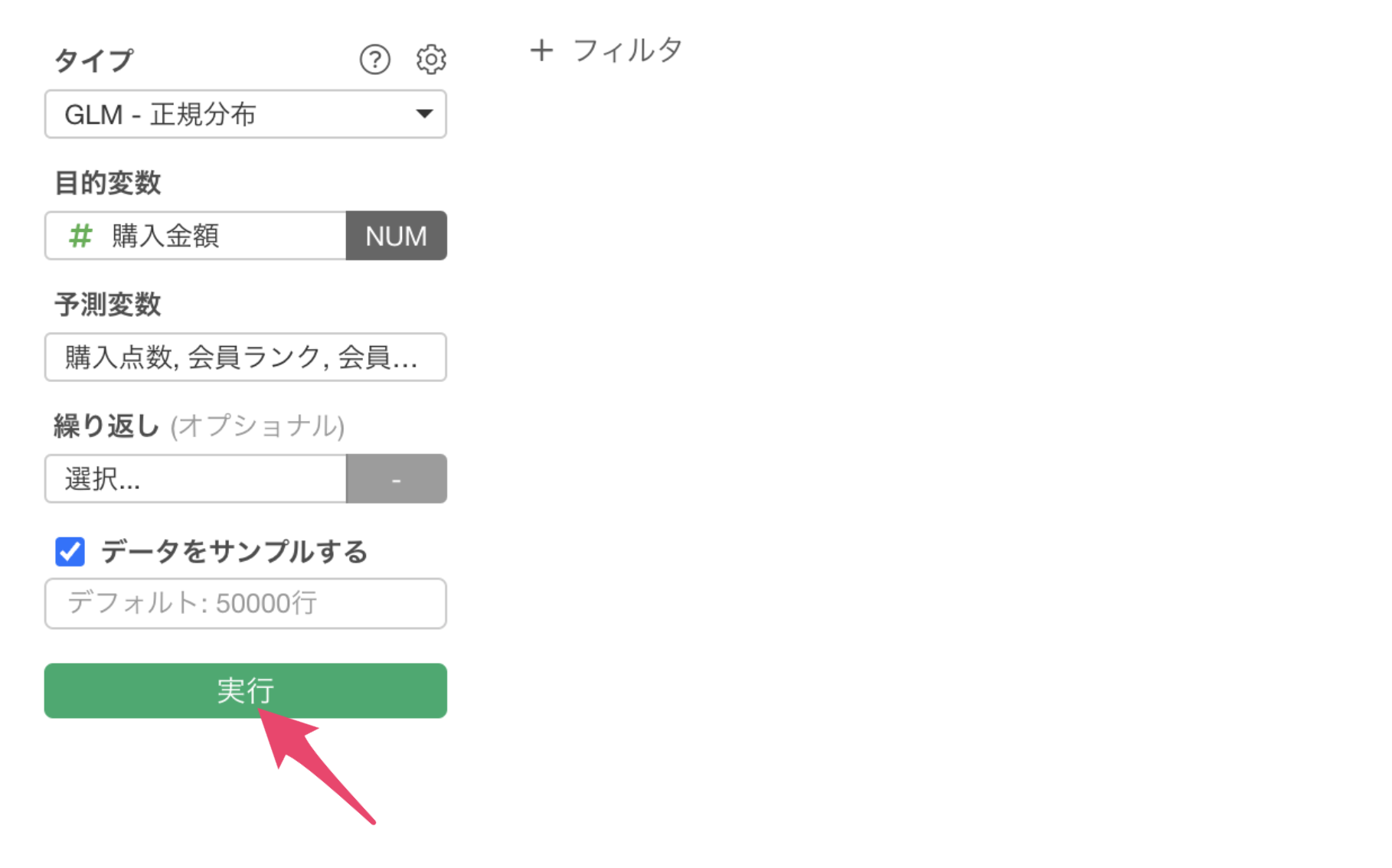
結果の解釈
一般化線形モデルでは、購入金額を予測・説明するために各タブの情報を確認できます。
多重共線性
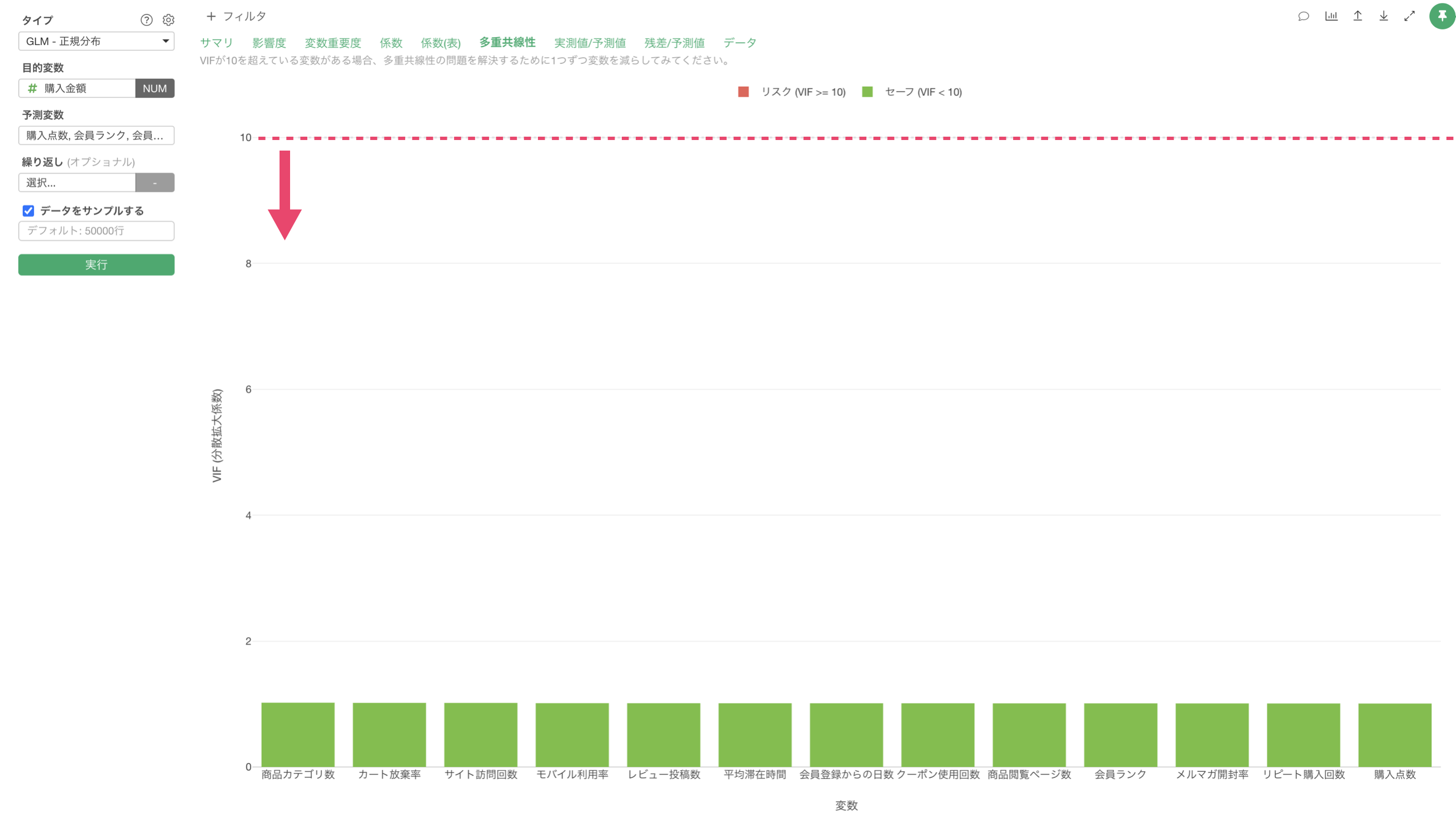
「多重共線性」タブをクリックすると、予測変数間の相関が強すぎる(VIF > 10)組み合わせがないかを確認できます。VIFが10以上の変数がある場合、モデルの信頼性に影響を与える(傾きが不安定になる)可能性があるため、変数の選択を見直す必要があります。
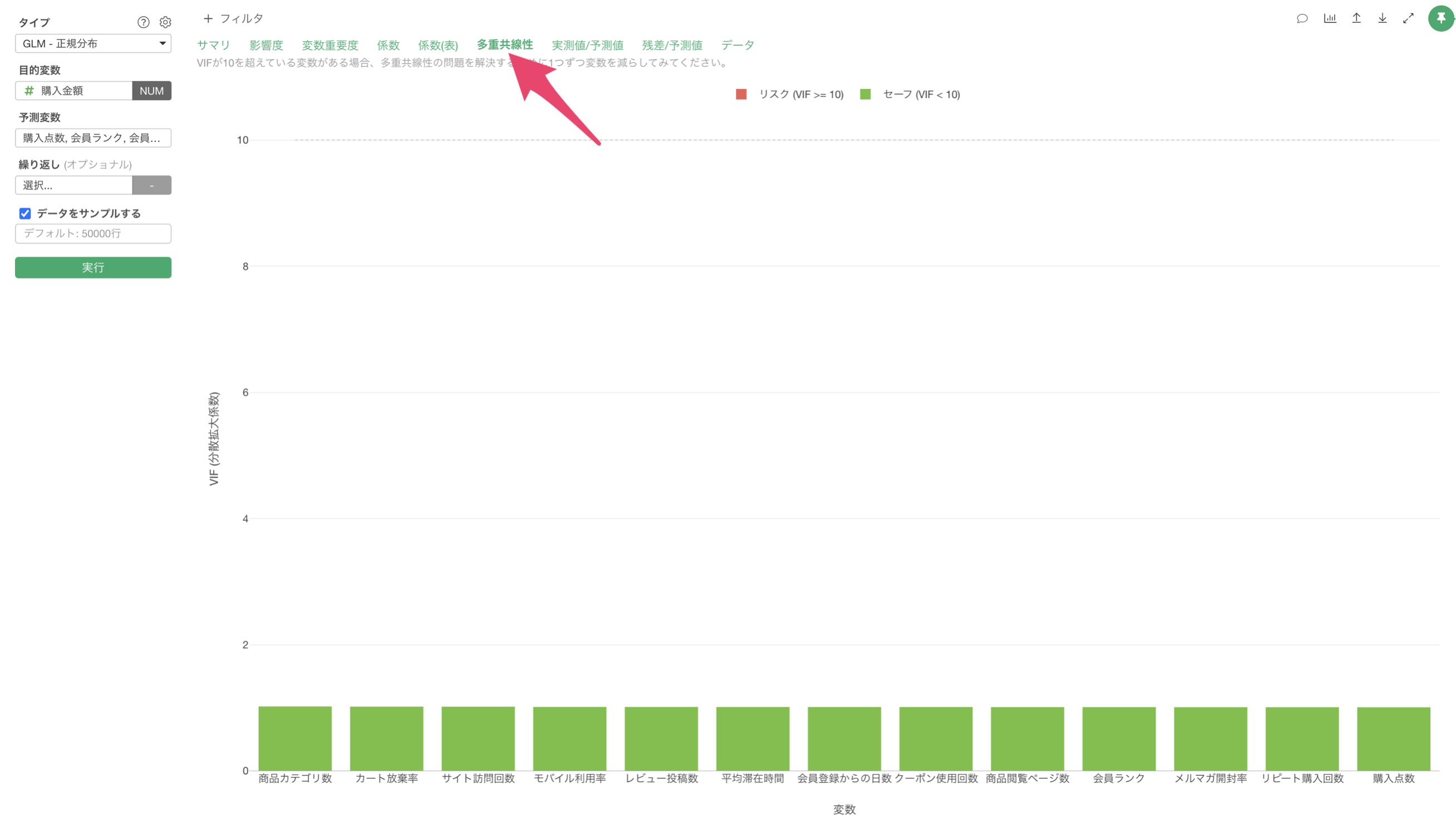
今回の結果は、VIFが10以上のものはないため、予測変数同士に相関が強すぎる変数の組み合わせがないため、モデルが不安定であることはないことがわかります。
変数重要度
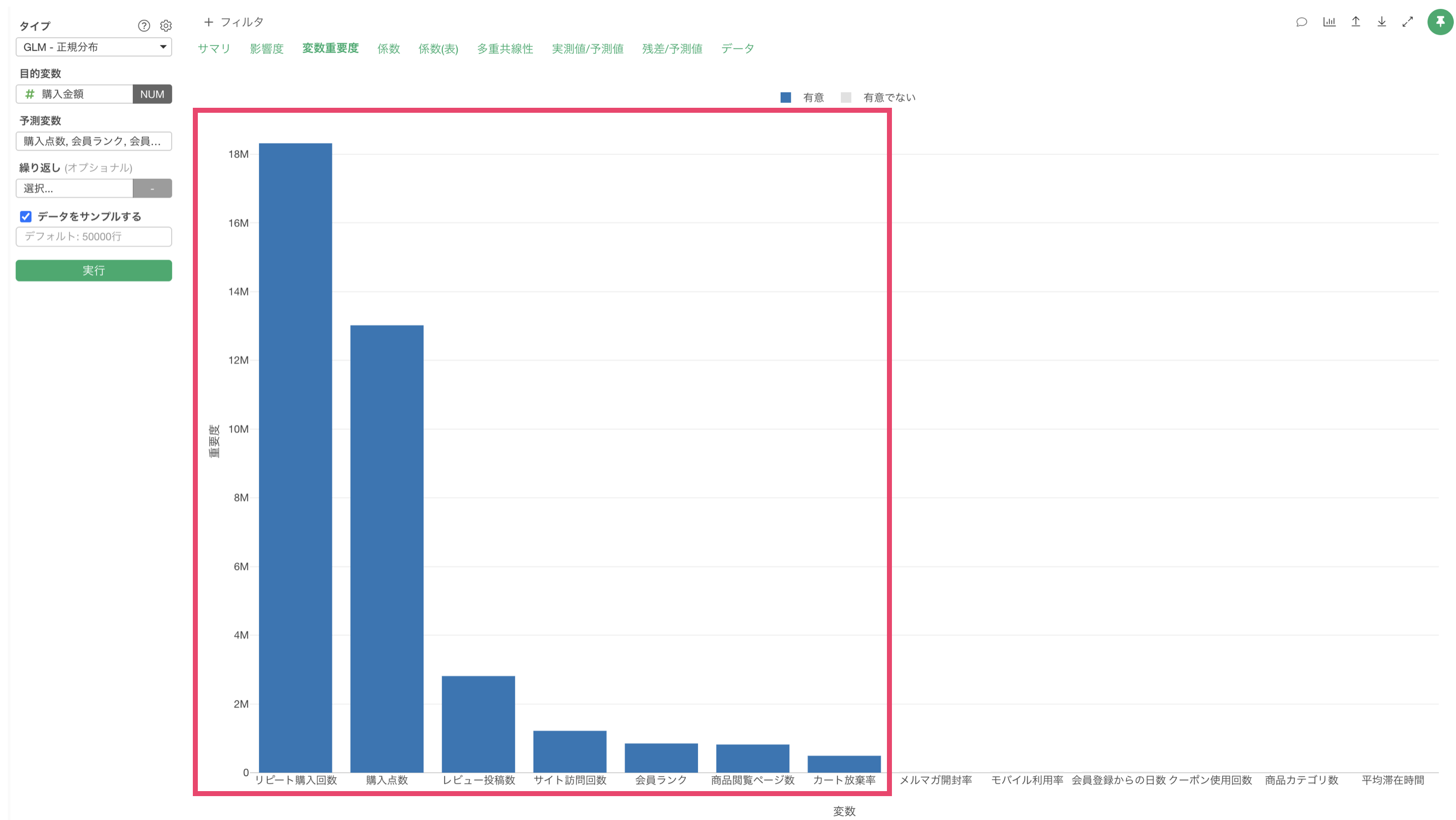
「変数重要度」タブをクリックすると、目的変数を予測する上でどの変数が重要なのかを確認することができます。
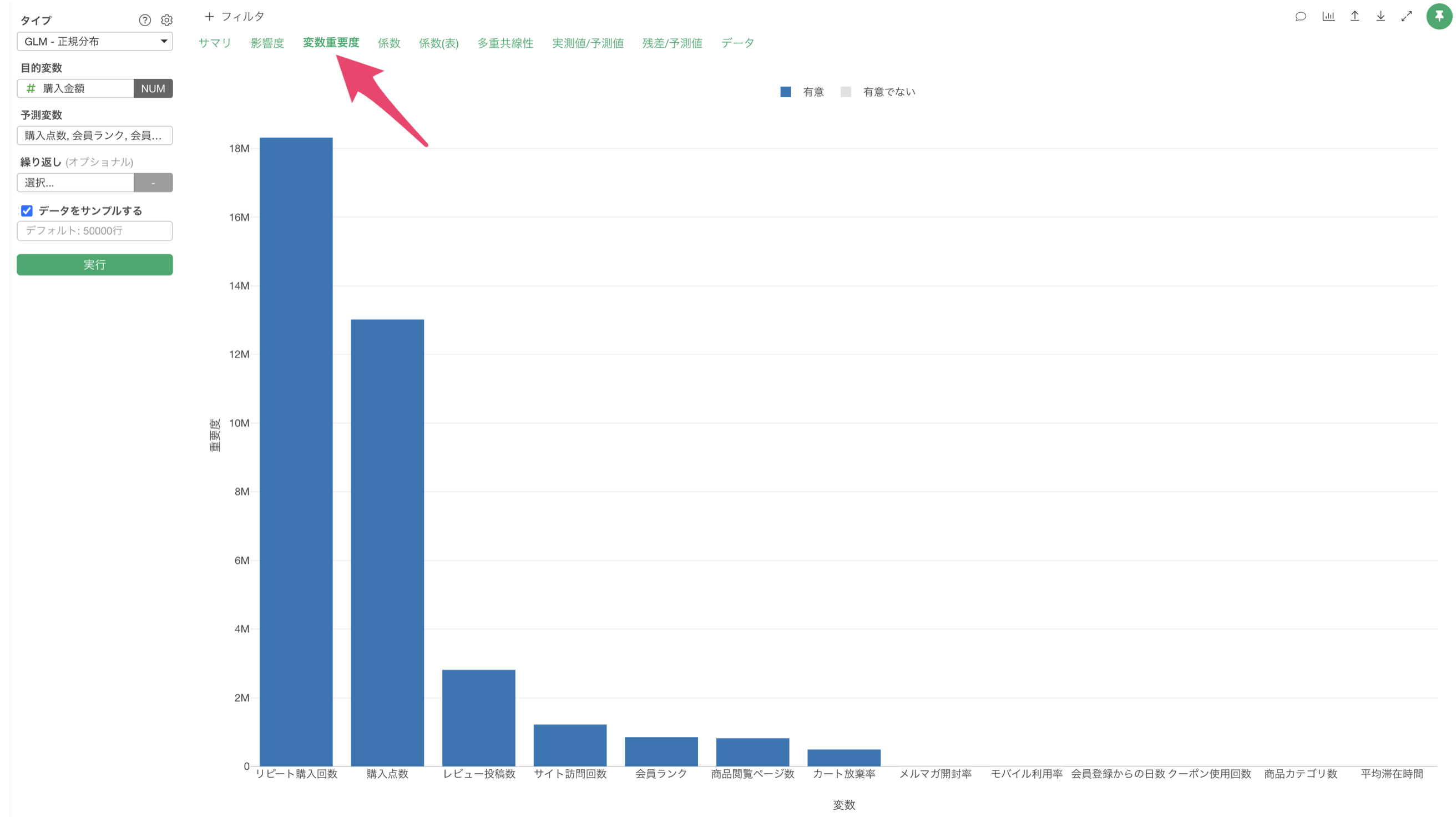
この結果から、購入金額の予測に最も重要な変数は生リピート購入回数であり、次いで購入点数、レビュー投稿数の順となっていることがわかります。
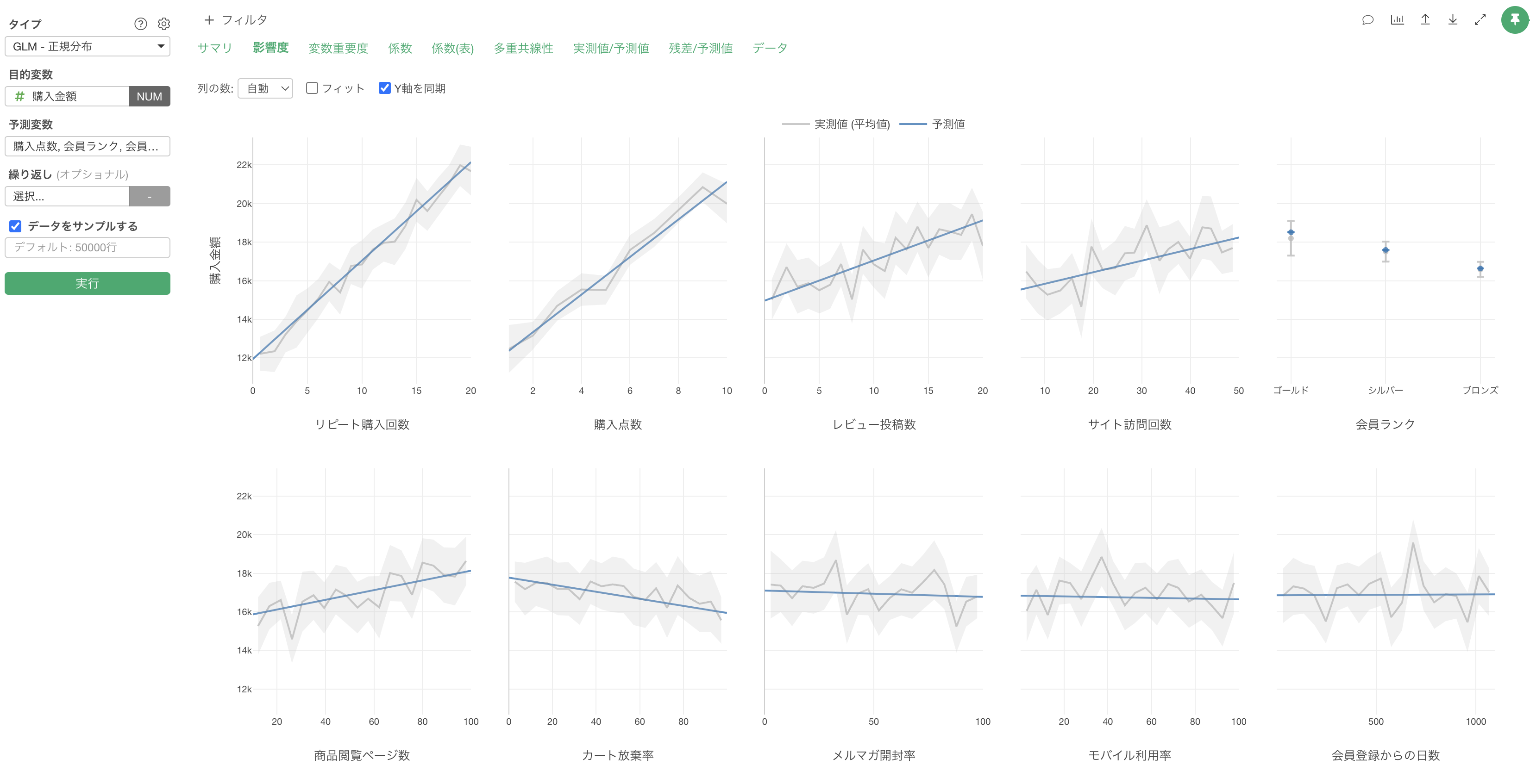
影響度
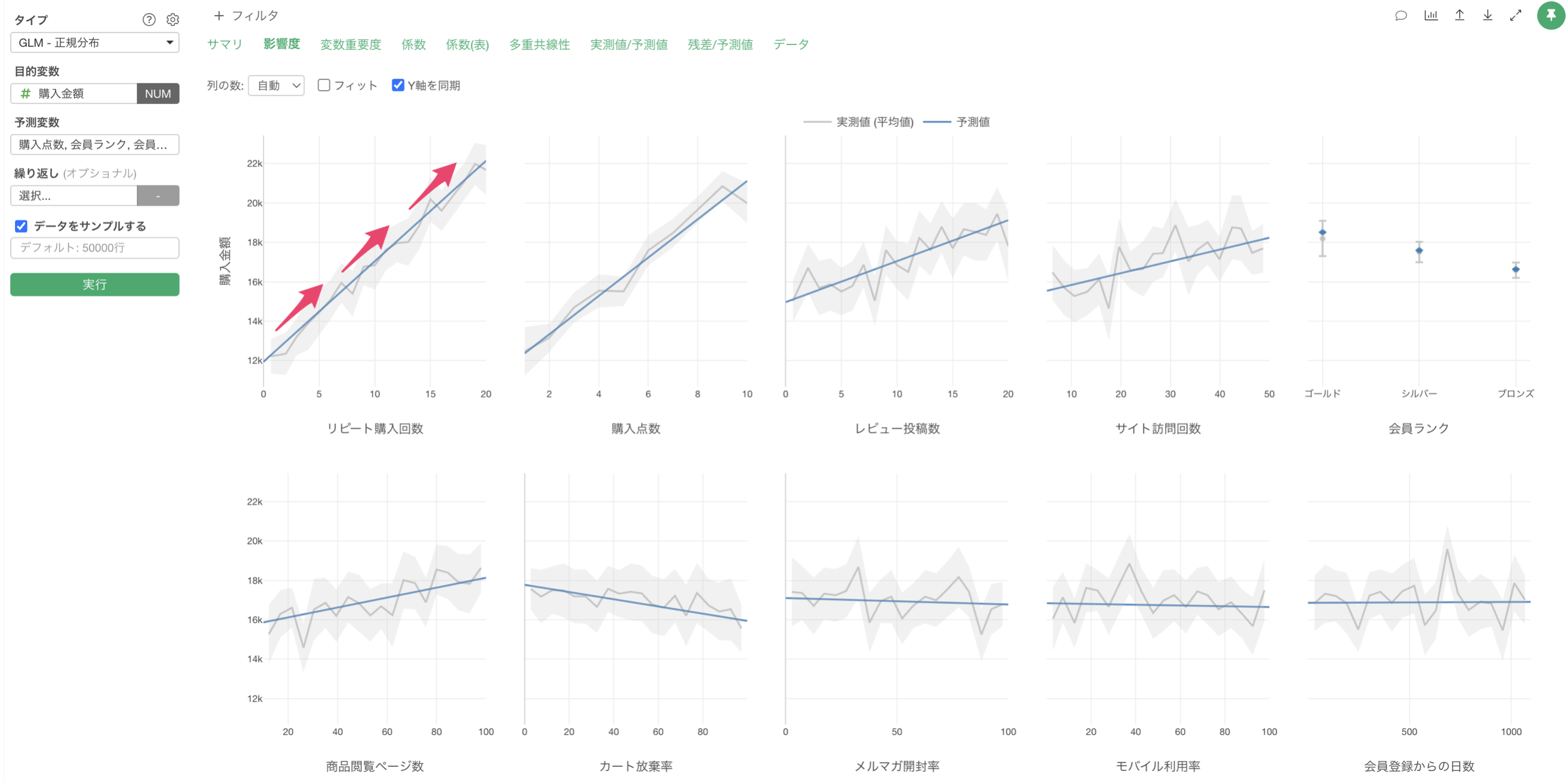
「影響度」タブでは、各予測変数が製造時間に与える影響の方向と強さを確認することができます。
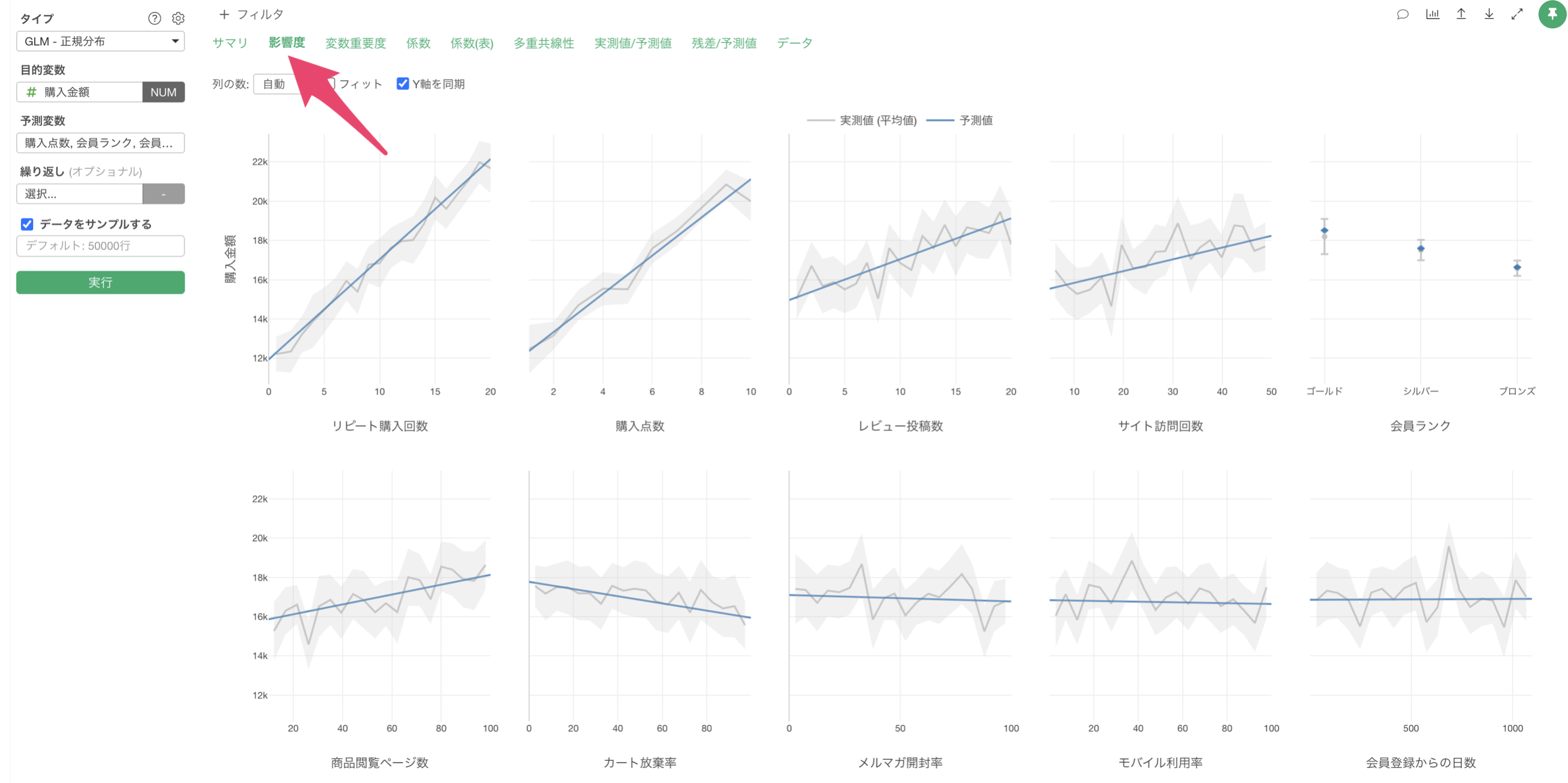
例えば、リピート購入回数が増えると、購入金額も増えることが確認出来ます。
例えば、会員ランクが「ゴールド」の場合は、他に比べて購入金額が高いことがわかります。一方で会員ランクが「ブロンズ」の場合は、購入金額が低い結果となっています。
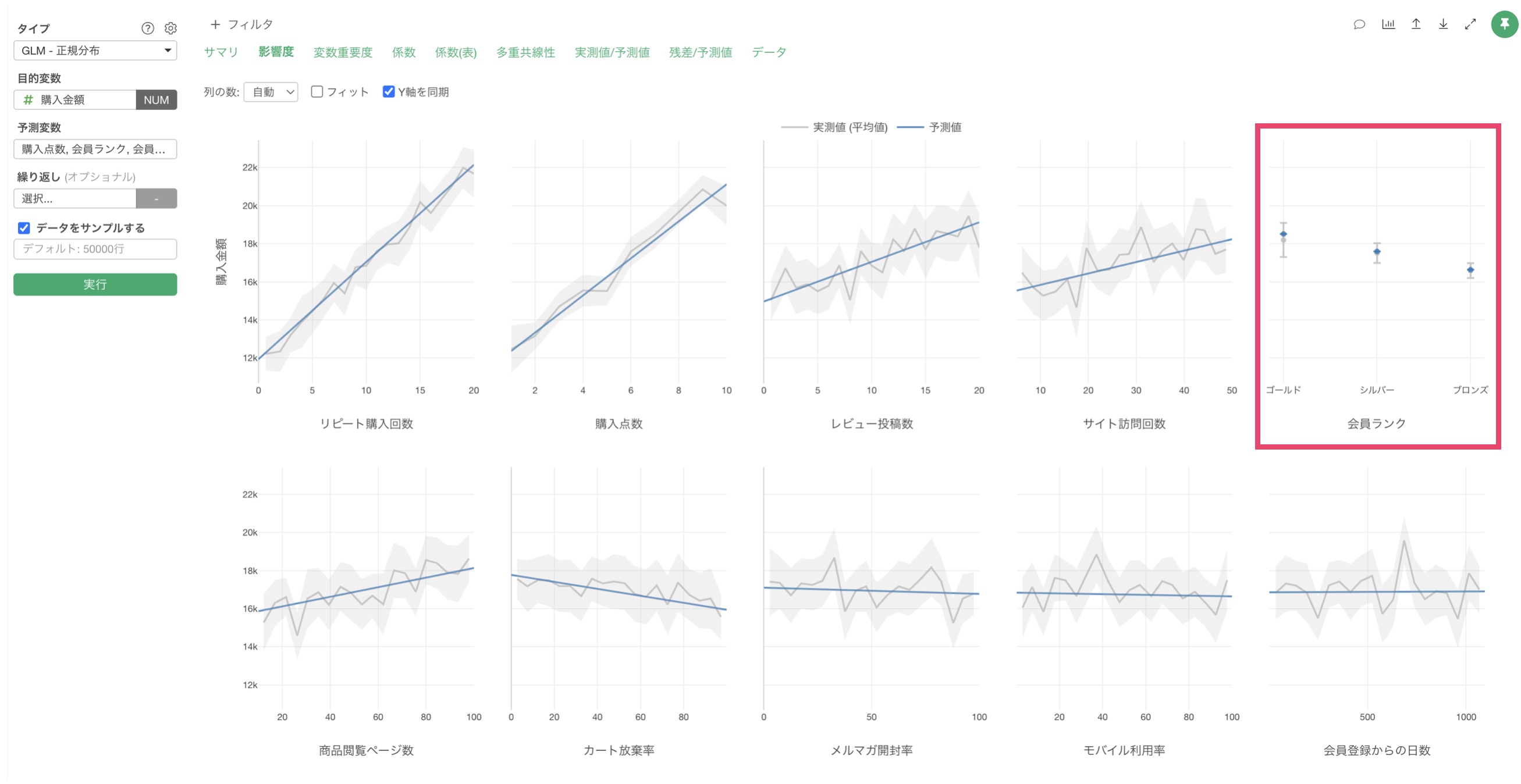
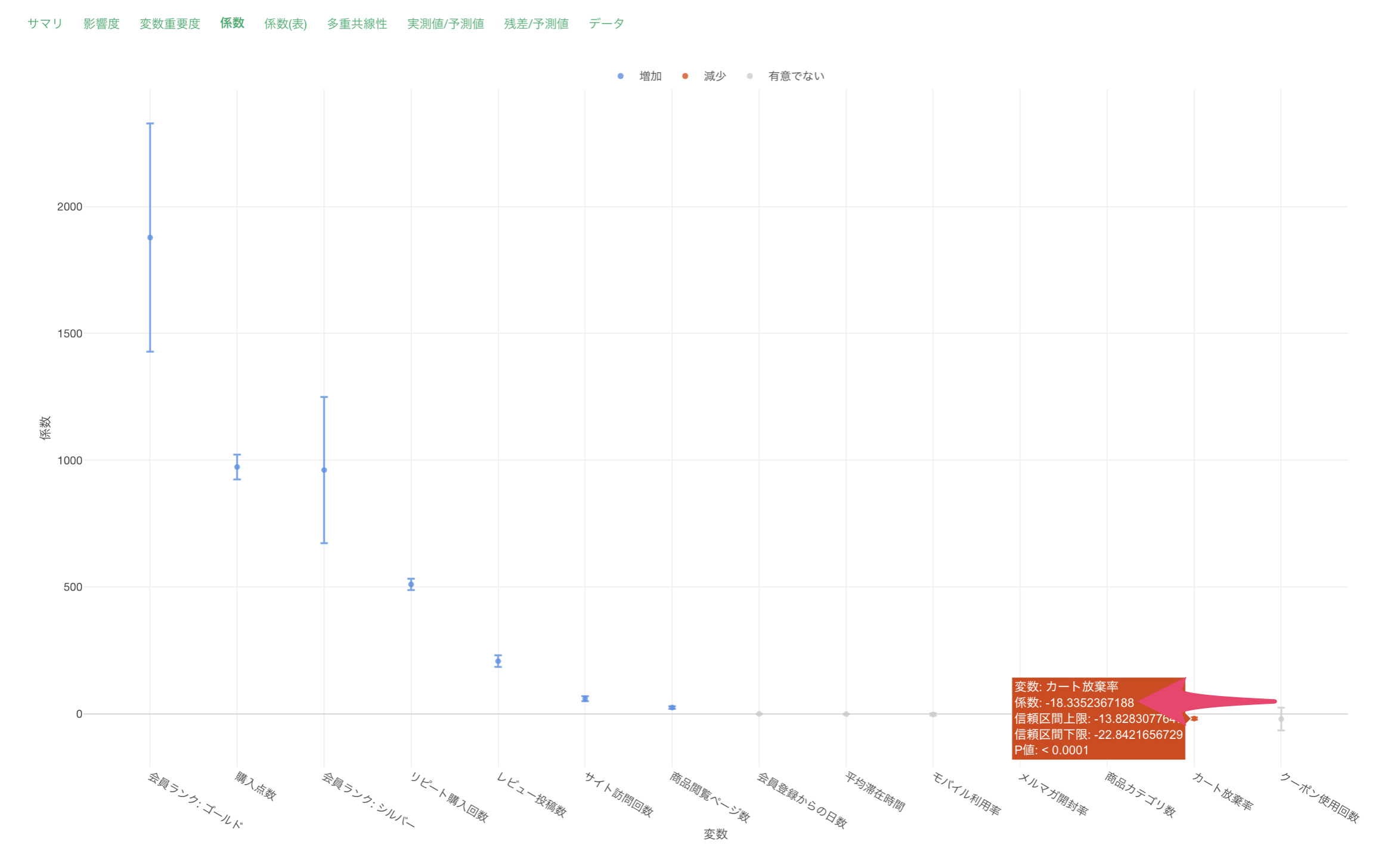
係数
「係数」タブでは、各予測変数の係数とその統計的有意性を確認することができます。
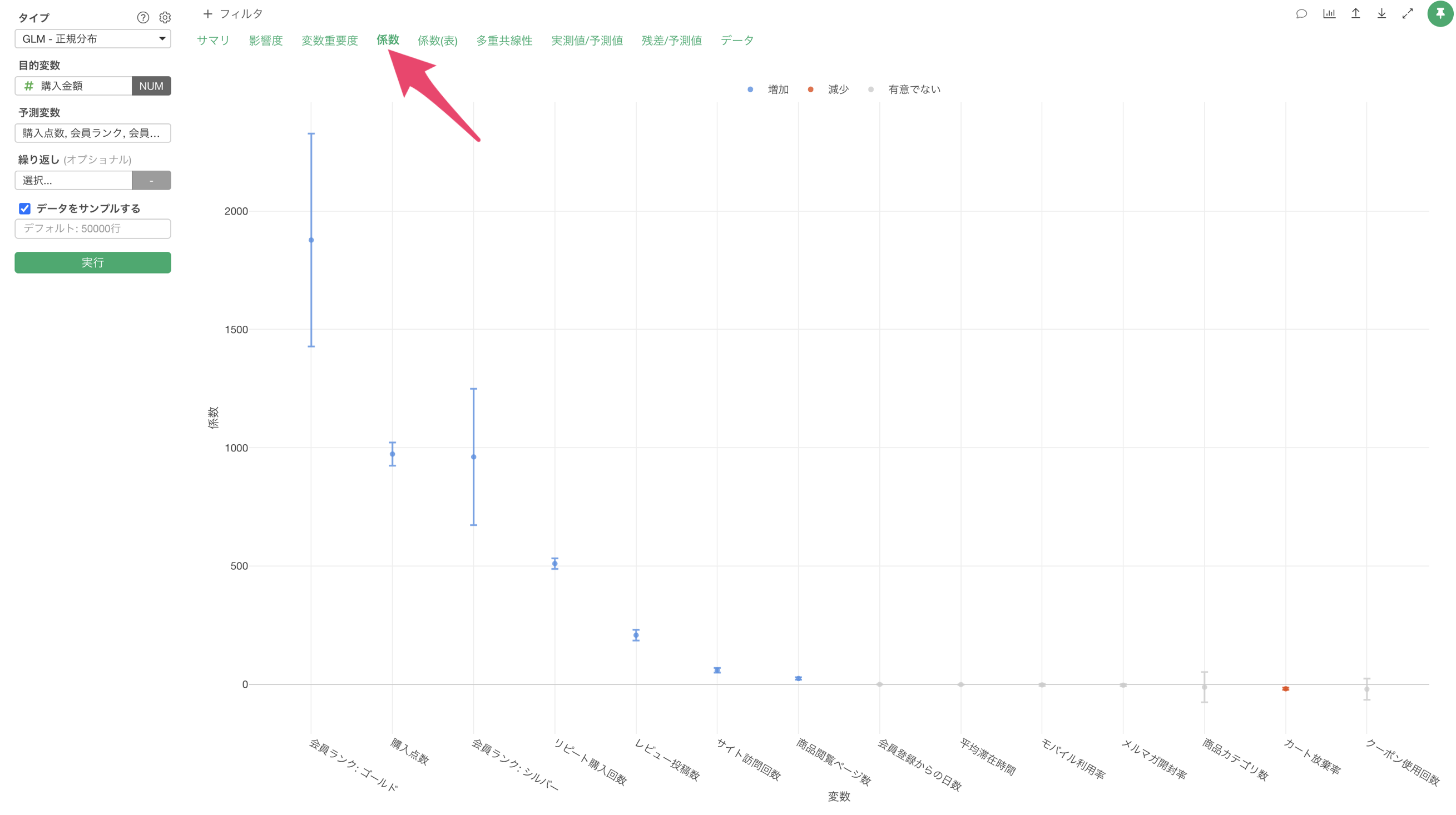
この結果から、各変数の効果の大きさを数値で確認できます。また、P値が0.05未満の変数は、統計的に有意な影響を持っていると判断できます。
会員ランクがブロンズからゴールドになった時の係数が1877であり、この場合は購入金額が1,877ドル増えることを意味します。
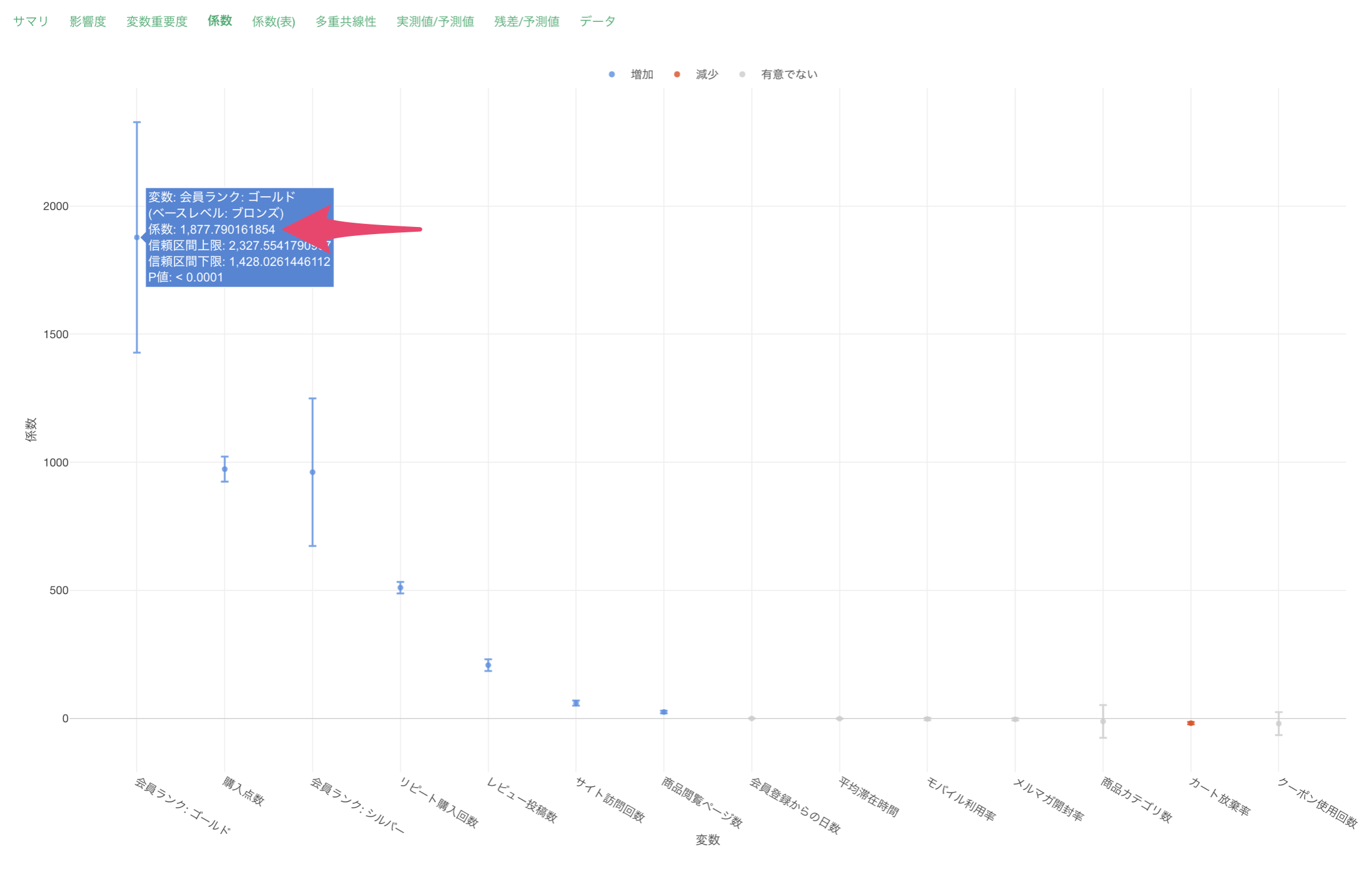
カート放棄率の係数が-18.3ですが、この場合はカート放棄率が1単位上がると、購入金額が18.3ドル減少することを意味します。
サマリ
「サマリ」タブをクリックすると、モデル全体の予測精度を確認することができます。

R2乗は目的変数の値のばらつきのうち、このモデルに使われている予測変数によって説明される割合を示します。
今回はR2乗が0.815のため、モデルが目的変数のばらつきの約81.5%を説明できることを示しています。0.8を超える値は比較的高い説明力を示し、実務的な予測モデルとして十分な精度があると判断できます。

4. まとめ
一般化線形モデル(GLM - 正規分布)は、ECサイトの購入金額分析のような連続的な目的変数に対する要因分析に適しています。今回の分析では、リピート購入回数や購入点数が購入金額に強い影響を持つことが明らかになりました。こうした知見は、売上向上施策の優先順位付けやリソース配分の意思決定に活用できます。
参考資料
- アナリティクス・ギャラリー - リンク