t検定(集計済みデータ)の使い方
t検定は、2つのグループ間の平均値の差が統計的に意味のある差なのかを判断するための統計的手法です。集計済みデータのt検定は、生データへのアクセスが制限されている場合や、大規模なデータを扱う際に特に有効です。
この手法の特徴は、観測された差が偶然によるものなのか、それとも実質的な改善の結果なのかを、統計的な観点から判断できる点にあります。各グループの平均値、標準偏差、サンプルサイズさえあれば分析可能なため、様々な業界での改善施策の効果を客観的に評価できます。特に、大規模なデータを扱う場面や、複数の部門間でのベンチマーク比較を行う際に威力を発揮します。
1. どういった時に使えるのか
集計済みデータのt検定は、幅広い分野での効果検証や比較分析に活用できます。新旧の製造方法の比較、異なる教育手法の効果測定、医療処置の効果比較など、平均値の差を統計的に評価する場面で特に有用です。
品質管理や効果測定においても重要な役割を果たします。製品の品質指標、顧客満足度スコア、業務効率指標など、重要な指標の改善効果を客観的に評価できます。また、異なる部門間や地域間でのパフォーマンスの違いを比較する際にも活用できます。
参考となるデータ例:
- 製品の品質評価スコアの比較データ
- 顧客満足度調査の結果比較データ
- 業務改善前後の処理時間データ
- アプリケーションの起動時間の比較データ
2. ユースケース
製造部門での使い方
- 製造部門では、新しい製造方法の効果を検証する際に使えます。
- 具体的には、製品の品質スコアを比較することで、新製造方法の有効性を統計的に確認できます。
- これにより、新製造方法の本格導入や改善点の特定に活用できます。
教育機関での使い方
- 教育機関では、新しい教育プログラムの効果を評価する際に使えます。
- 生徒の成績データを比較することで、プログラムの有効性を客観的に示すことができます。
- これにより、教育プログラムの改善や予算配分の判断材料として活用できます。
品質管理部門での使い方
- 品質管理部門では、品質改善施策の効果を検証する際に使えます。
- 不良品率などの品質指標を比較することで、改善施策の効果を定量的に評価できます。
- これにより、改善施策の水平展開や追加対策の必要性を判断できます。
商品開発部門での使い方
- 商品開発部門では、商品改良の効果を評価する際に使えます。
- 顧客満足度スコアを比較することで、改良の効果を客観的に示すことができます。
- これにより、さらなる改良の方向性や製品戦略の判断材料として活用できます。
3. Exploratoryでt検定(集計済みデータ)を実行する
使用するデータ
今回は「アプリの起動速度データ」を使用します。データはこちらからダウンロードが可能となっています。
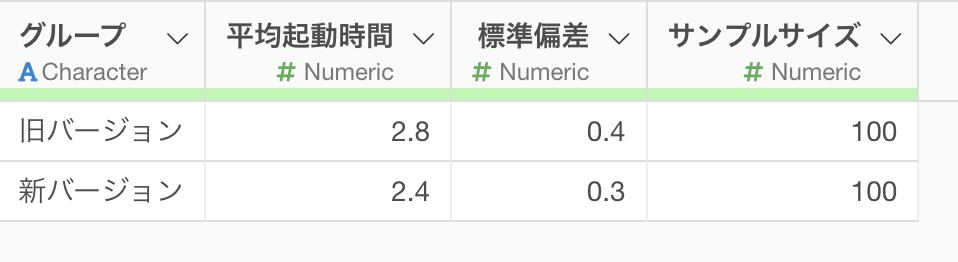
このデータは1行が1つのバージョンを表しており、列には「グループ」「平均起動時間」「標準偏差」「サンプルサイズ」といったデータがあります。
t検定(集計済みデータ)を実行するためには、以下のようなデータ構造が必要となります。
- グループを示す列(2つのグループが必要)
- 各グループの平均値を示す列(今回は起動時間)
- 各グループの標準偏差を示す列
- 各グループのサンプルサイズを示す列
アナリティクスを作成する
アプリパフォーマンス検証データから「アナリティクス・ビュー」を開きます。
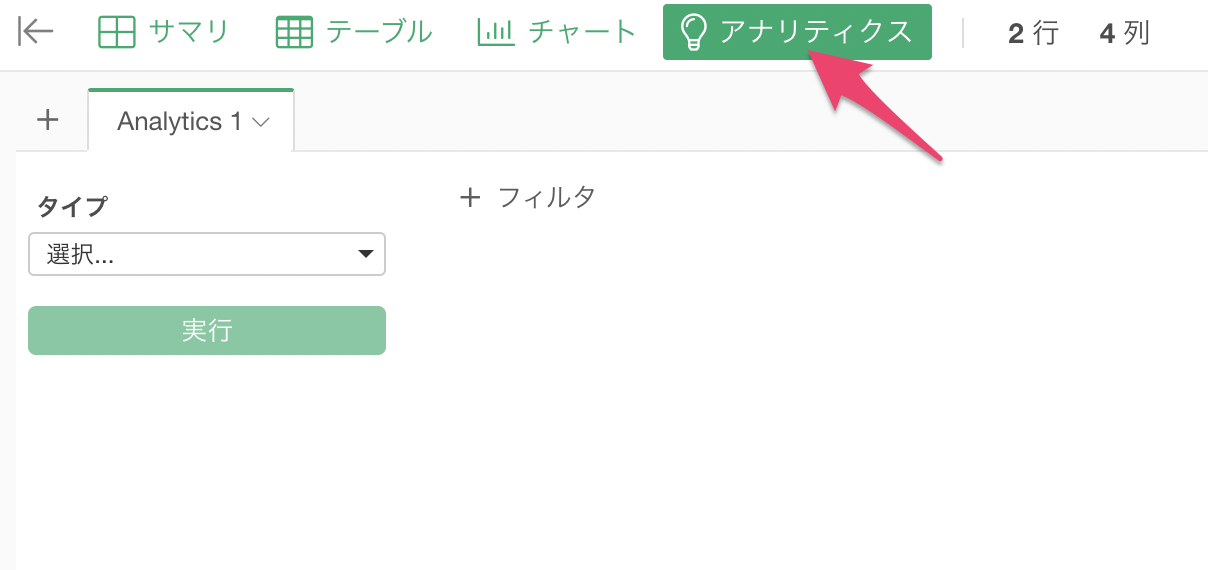
タイプに「統計的検定」を選び、「t検定 (集計済みデータ)」を選択します。
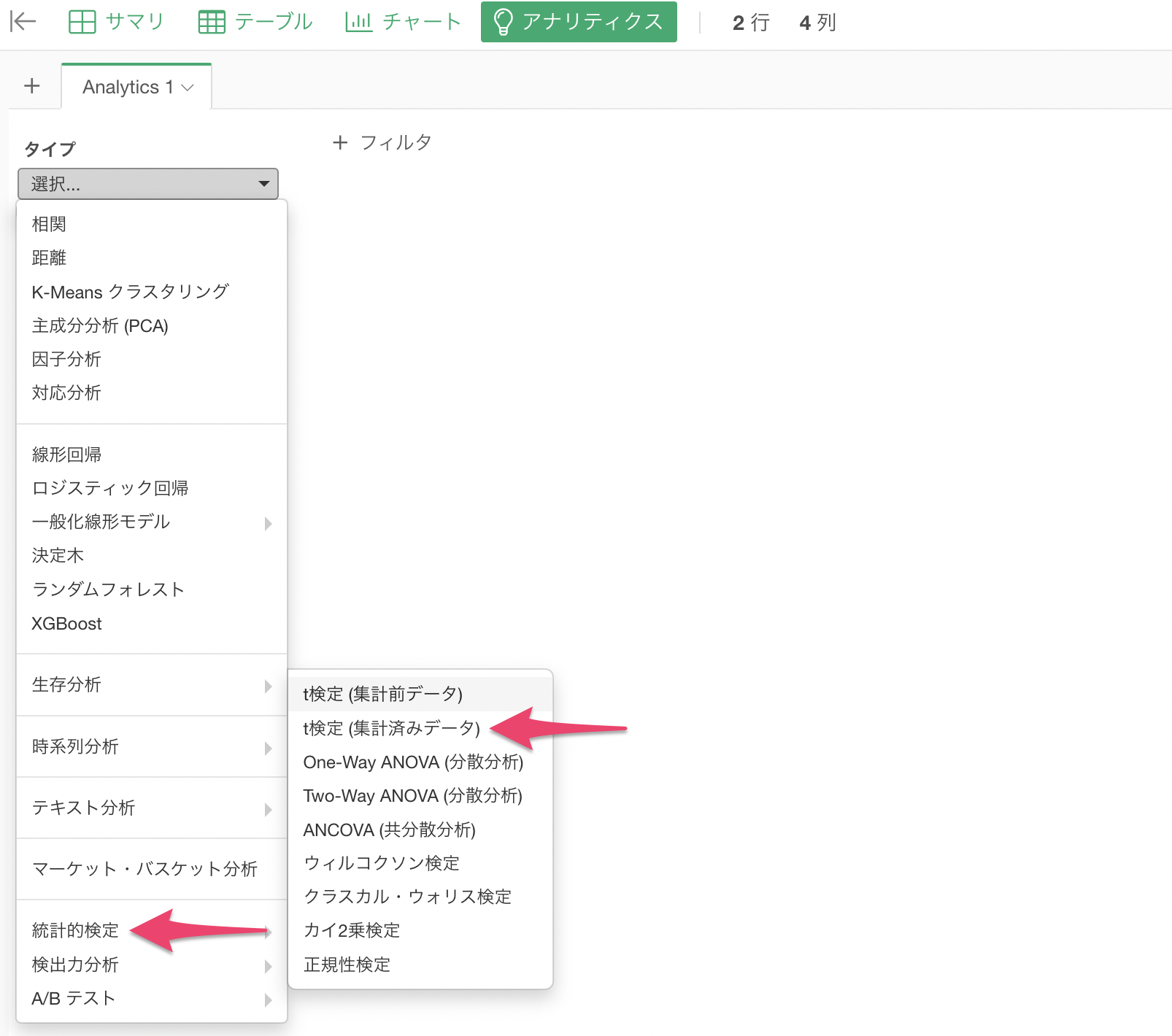
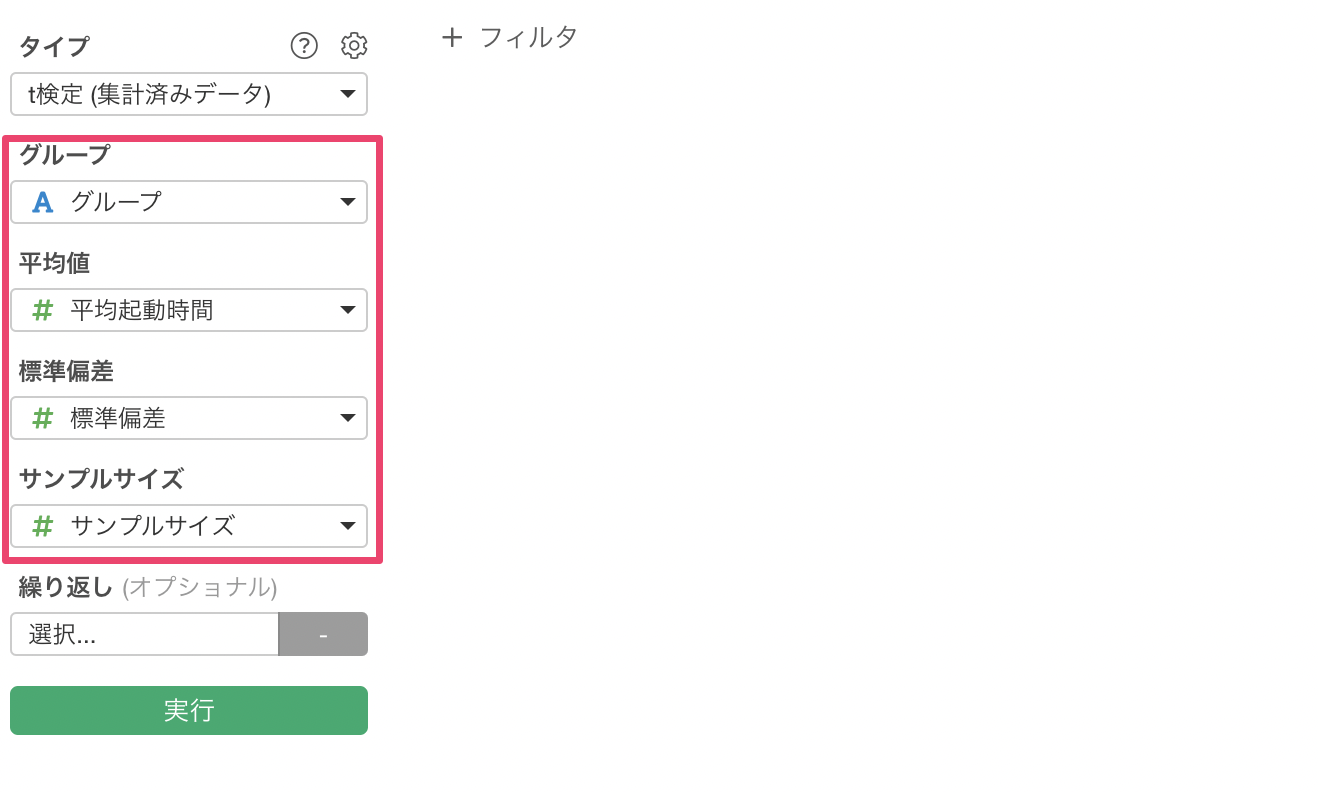
次に、各項目には以下のように設定します。
- グループ: 「グループ」の列
- 平均値: 「平均起動時間」の列
- 標準偏差: 「標準偏差」の列
- サンプルサイズ: 「サンプルサイズ」の列
最後に、「実行」ボタンをクリックして実行結果を確認します。
結果の解釈
t検定(集計済みデータ)では、2つのグループの平均値の差が統計的に有意かどうかを解釈するためにサマリ、確率分布、平均値の差などの情報があります。
サマリ
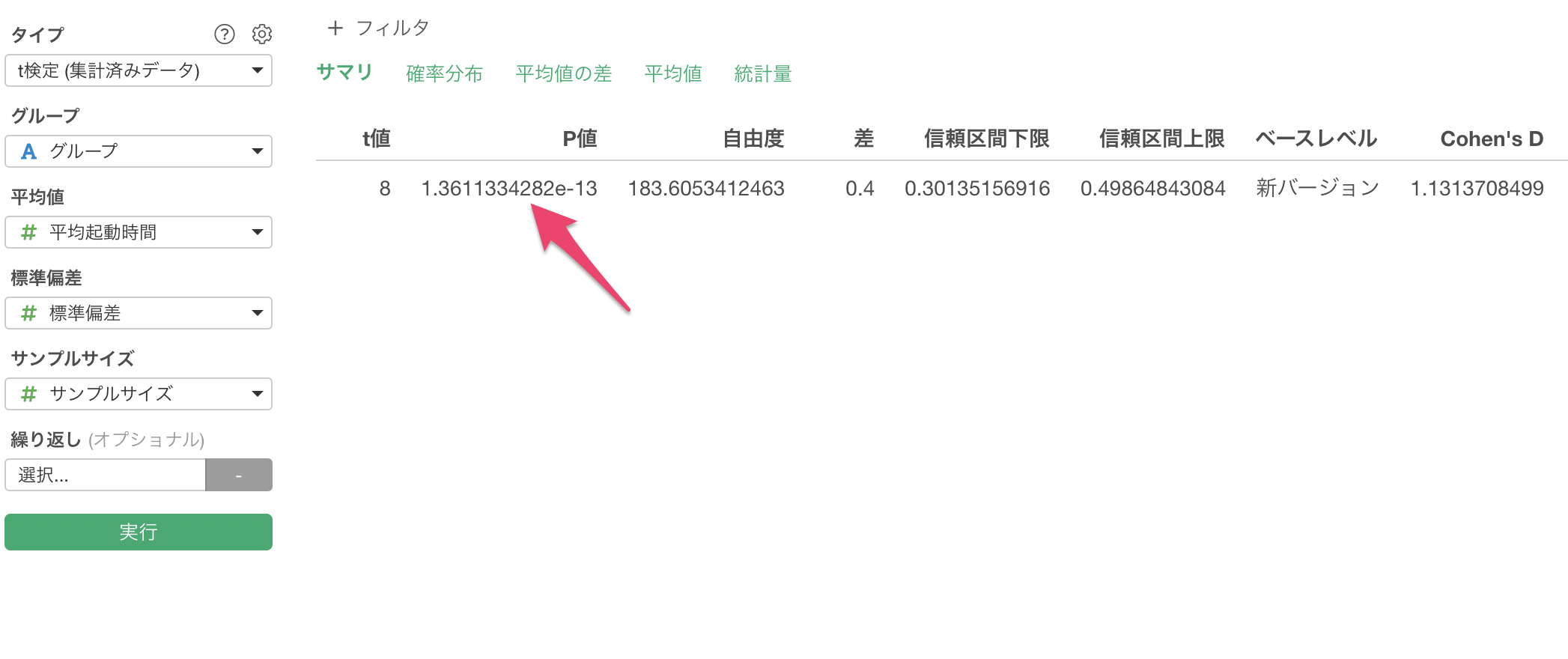
「サマリ」をクリックすると、検定結果の概要を確認することができます。

このデータの場合、p値が0.05未満となっており、新バージョンと旧バージョンの起動時間には統計的に有意な差があることがわかります。P値が1.36e-13の場合は、1.36の10の-13乗となるため、限りなくP値が小さいということを表します。
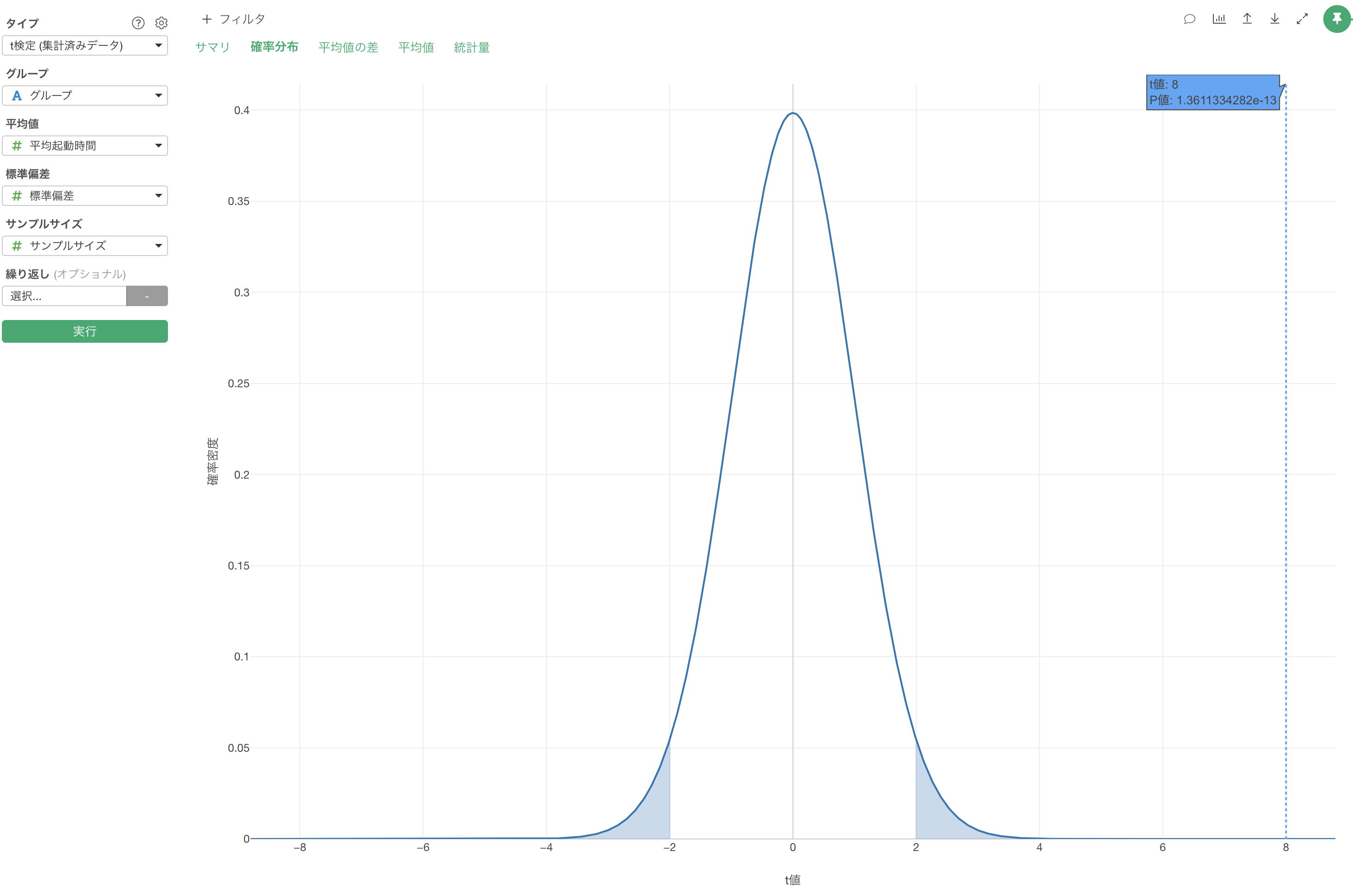
確率分布
「確率分布」をクリックすると、t分布上での検定統計量の位置を確認することができます。
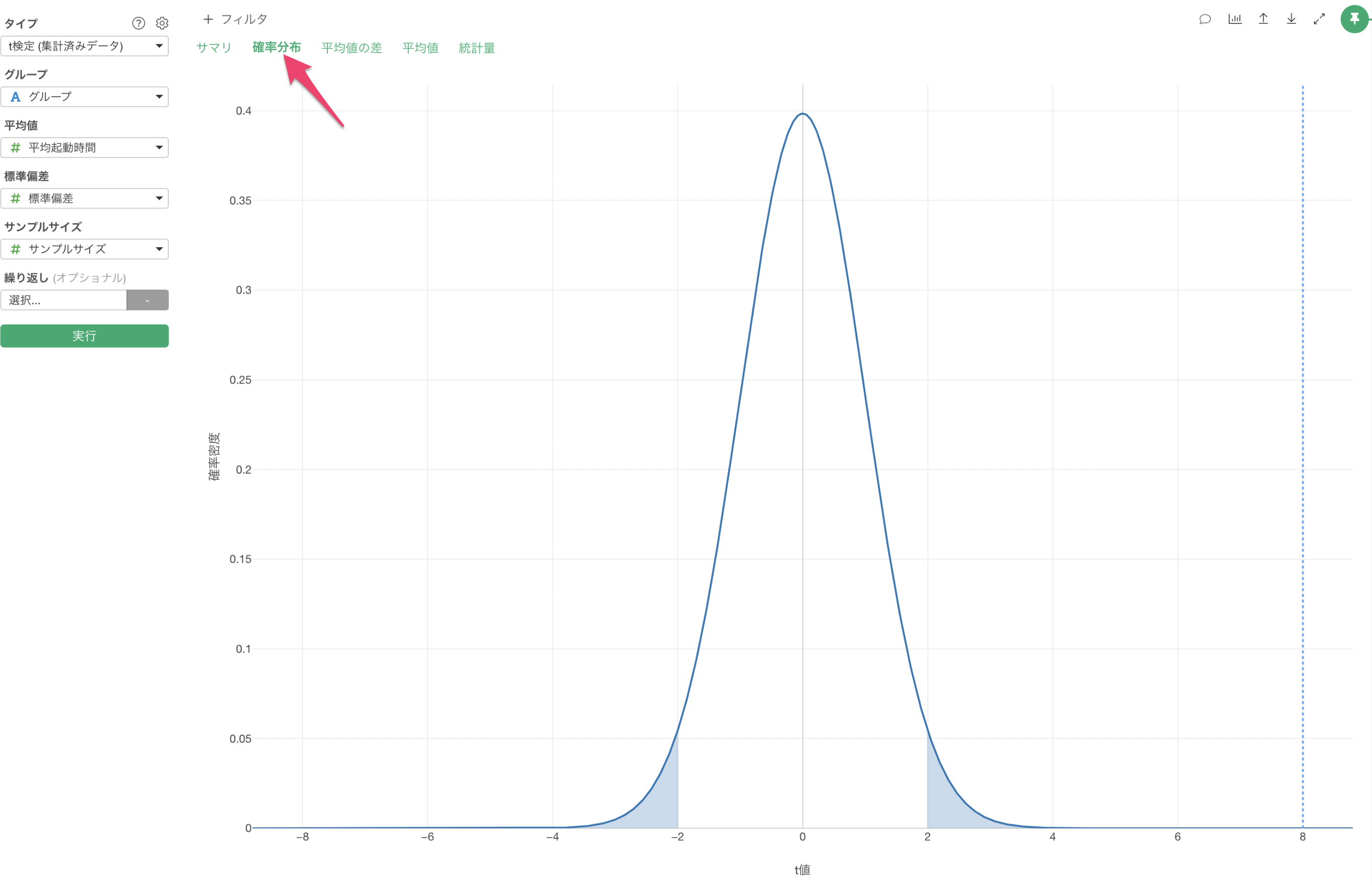
この結果から、観測されたt値が棄却域に入っており、帰無仮説(「2つのバージョン間に差がない」という仮説)を棄却できることがわかります。つまり、パフォーマンスの改善は統計的に有意であると判断できます。

平均値の差
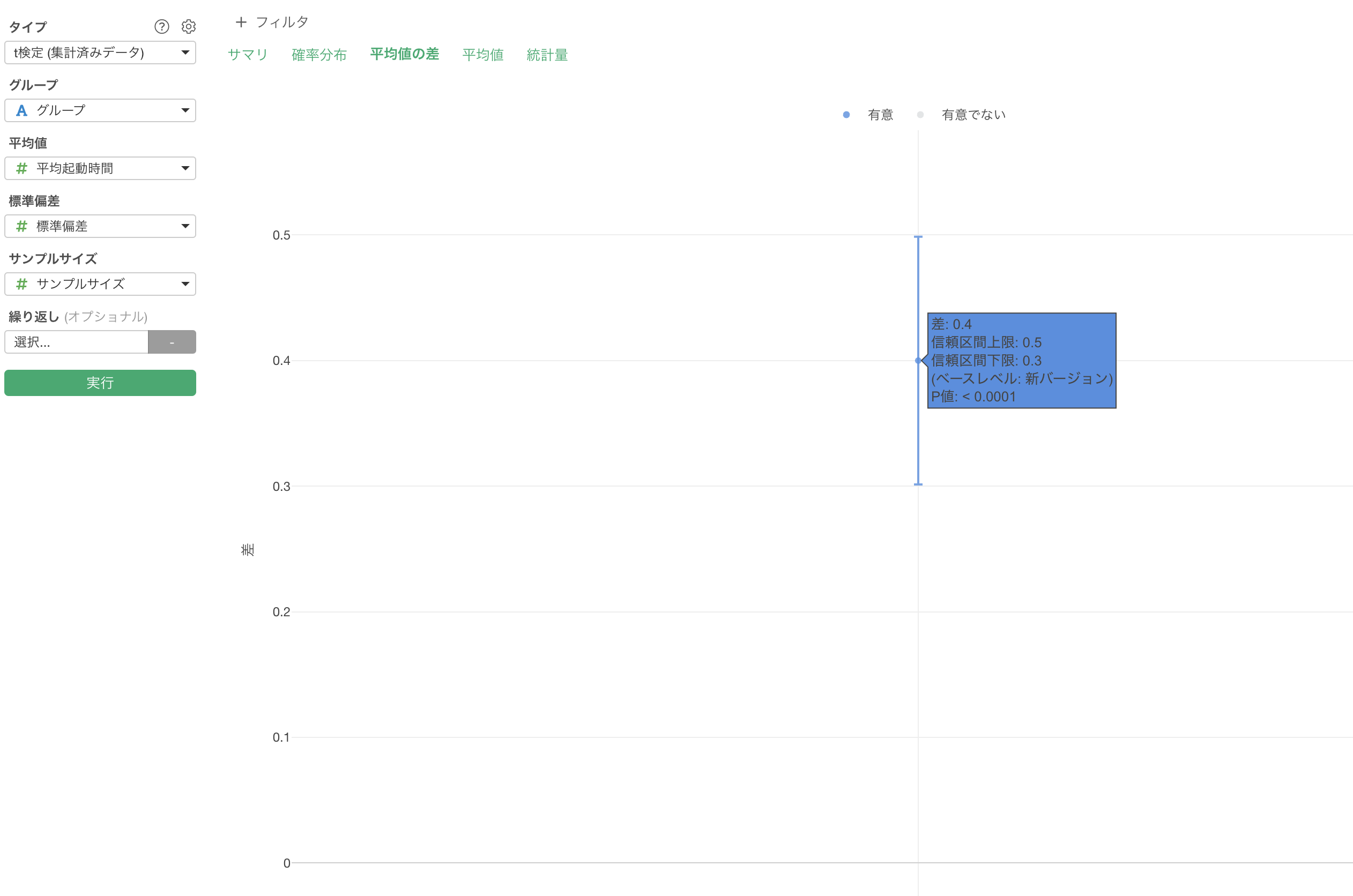
「平均値の差」をクリックすると、2つのグループの平均値の差とその信頼区間を確認することができます。
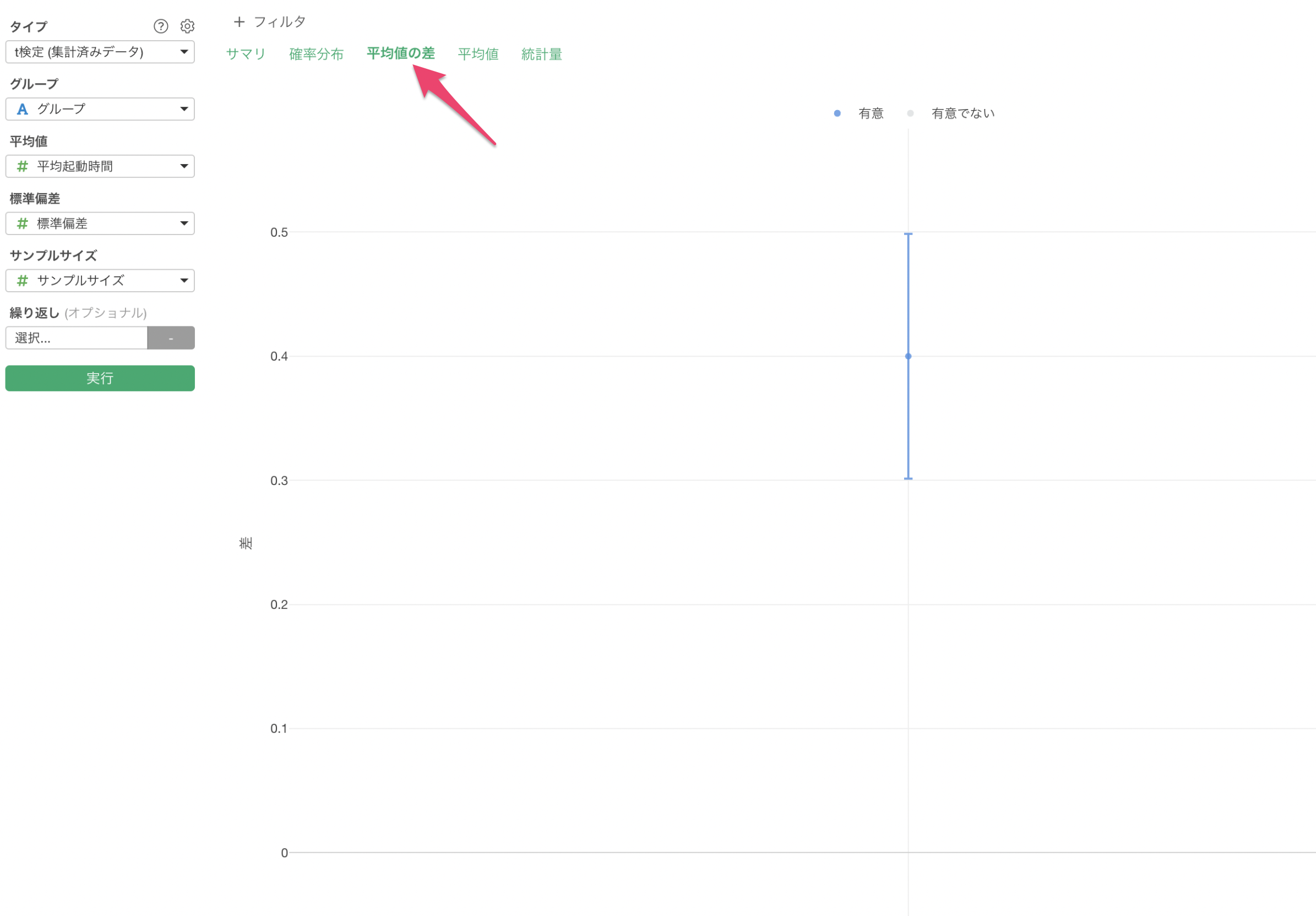
この結果から、新バージョンは旧バージョンと比べて平均して0.4秒の起動時間短縮が見られ、その差は統計的に有意であることがわかります。95%信頼区間から、この改善効果は安定して0.3〜0.5秒の範囲に収まると推定できます。
4. まとめ
t検定(集計済みデータ)は平均値の差の統計的有意性を評価する強力なツールです。今回の例では、新バージョンによってアプリの起動時間が0.4秒短縮され、その改善がp値としても統計的に有意性であることがわかりました。
このように集計済みデータのt検定は、生データにアクセスできない状況でも、平均値・標準偏差・サンプルサイズがあれば改善効果を客観的に評価できます。この特徴は、品質管理、教育効果の測定、製品開発など、幅広い分野での意思決定に活用できます。
統計的有意性を示すことで、「改善の効果がある」という主張の信頼性を高め、次のアクションにつなげることができます。
参考資料
- アナリティクス・ギャラリー - リンク