クラスカル・ウォリス検定の紹介
クラスカル・ウォリス検定とは統計的検定の手法の一つで、元データの分布が正規分布という前提がなくても使えるノンパラメトリック検定です。さらに、t検定のように対象となるグループの数は2つだけでなく、2つ以上を対象としても実行できるのも特徴です。
例えば、部署ごとの給料の平均値を可視化したバーチャートがあったとします。これらの部署の給料の平均値には違いがありますが、それが意味のある違いなのかどうかはこのバーチャートからでは判断できません。
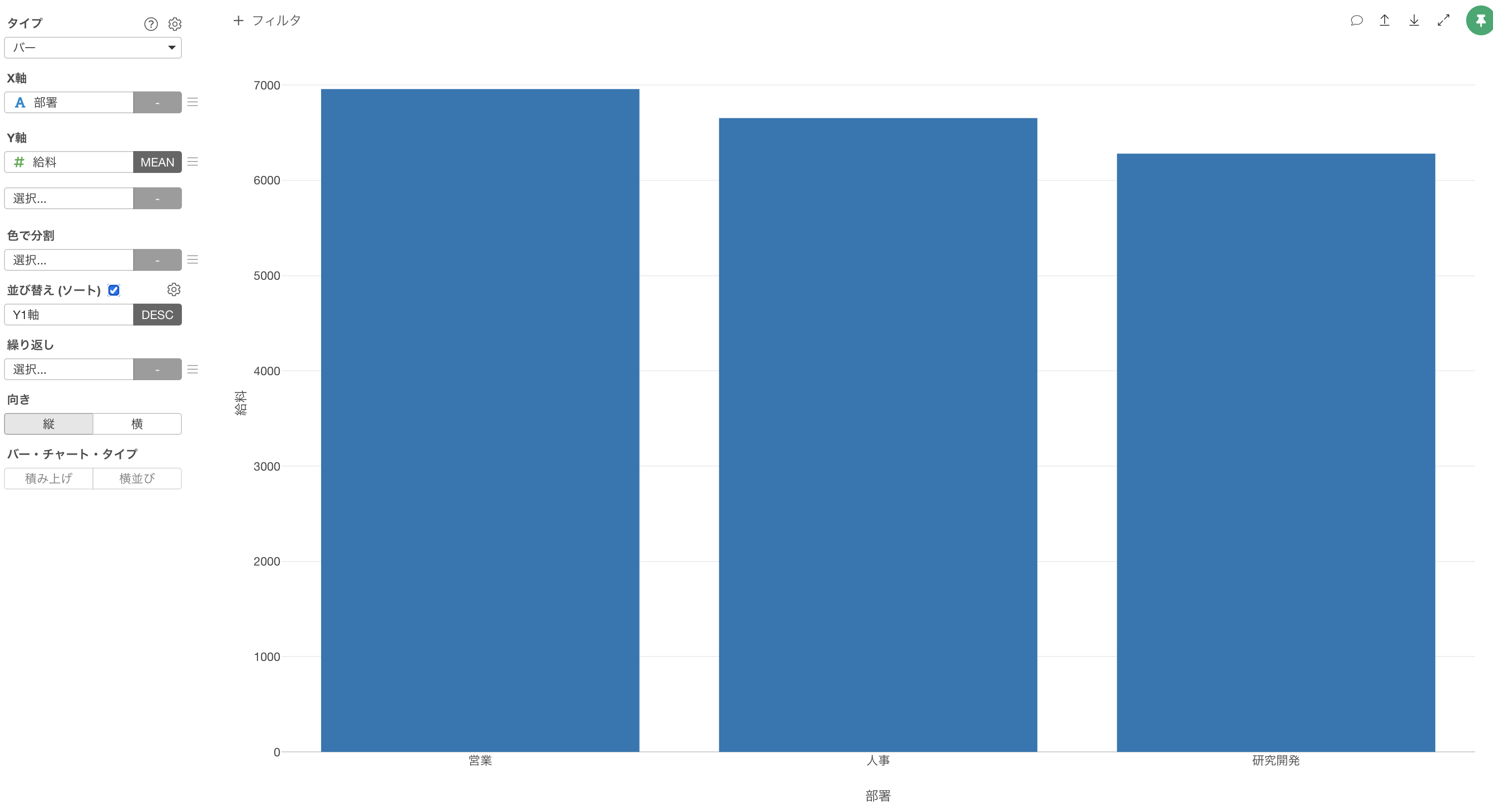
そこで、部署間の給料の差には、意味のある違いがあるのかどうかを知るために、クラスカル・ウォリス検定を使って検証していきます。
クラスカル・ウォリス検定検定を実行する
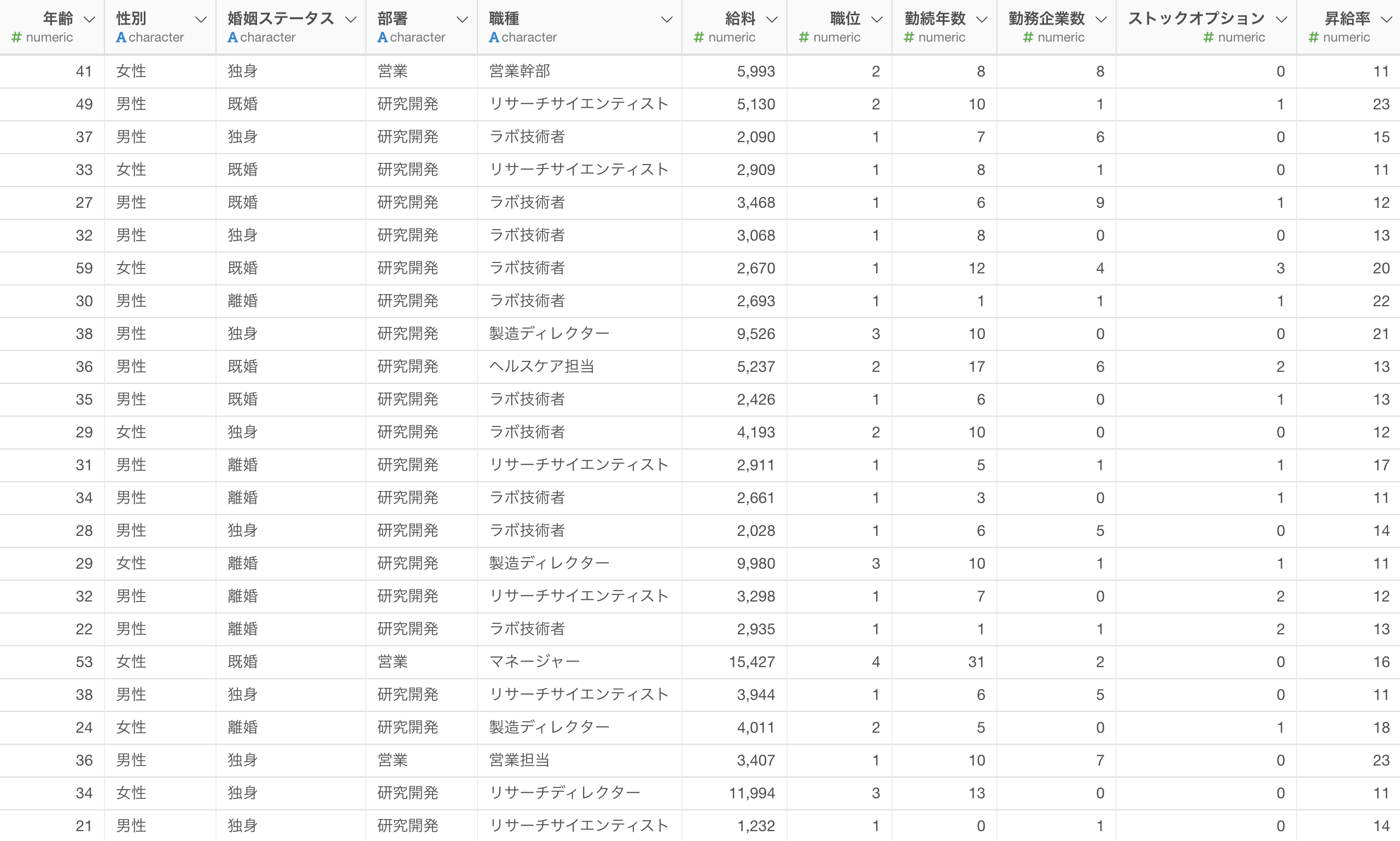
今回は、「部署」によって「給料」に違いがあるのかをクラスカル・ウォリス検定を使って調べていきます。ちなみに、部署には一意な値の数が3つあり「営業」と「研究開発」、「人事」があります。

アナリティクスビューを開き、タイプに「クラスカル・ウォリス検定」を選択します。
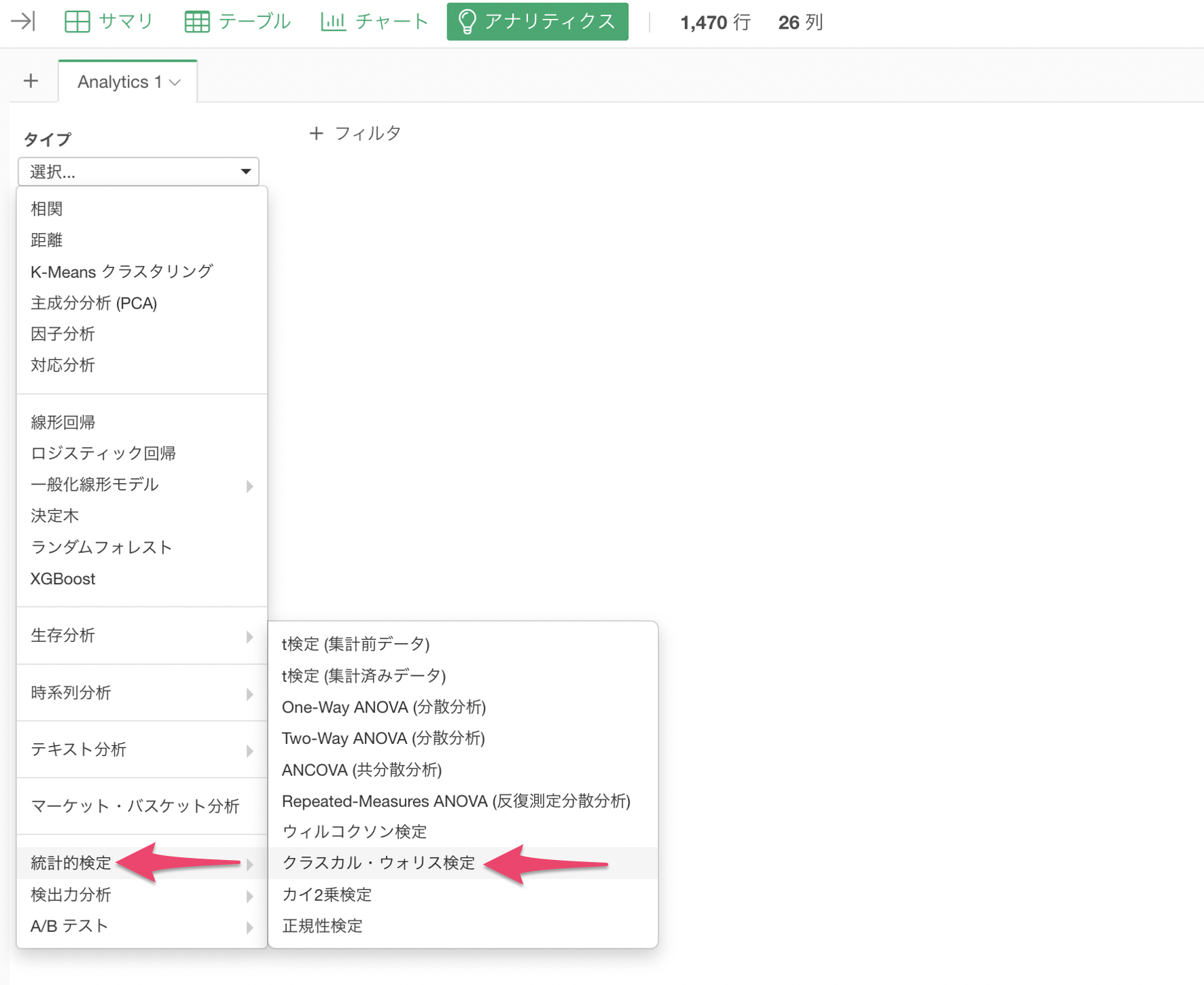
目的変数に「給料」を選び、説明変数に「部署」を選択します。
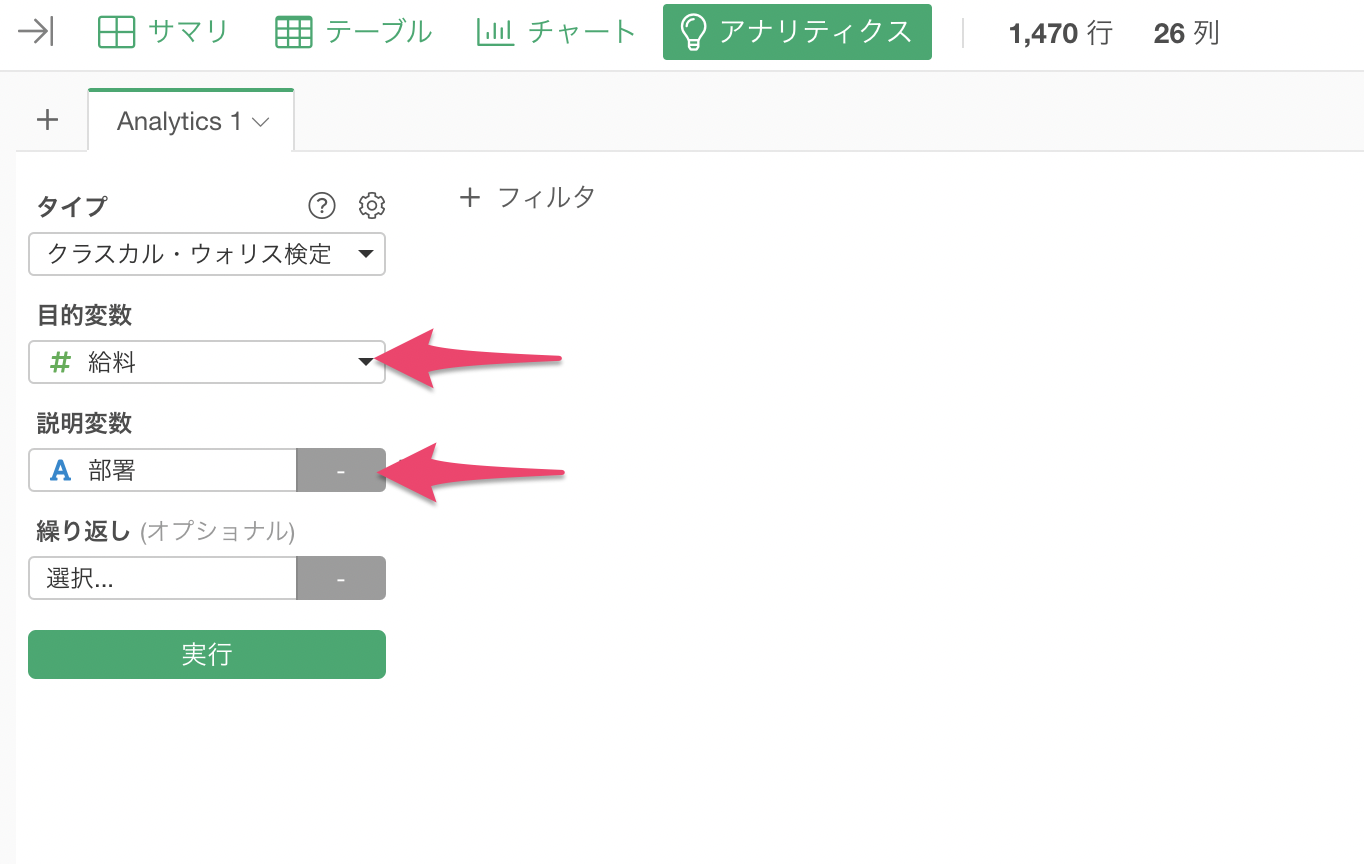
これにより、「部署」によって「給料」の差が有意かどうか調べるためのクラスカル・ウォリス検定が実行されました。

結果の解釈
サマリ
「サマリ」タブでは、検定の結果が有意かどうかを確認できます。部署によって給料に差がないことを前提とした時に、この結果が得られる確率を表すP値から有意かどうか判断ができ、一般的には0.05(5%)を下回ると有意であると言われています。

上記の場合はP値の末尾に「e-10」と表記されており、eがつく場合は、E表記や指数表記と呼ばれます。5.56e-10の場合は、5.56 * 10の-10乗を表し、P値がかなり小さいことがわかります。
確率分布
「確率分布」タブでは、使用したデータの自由度を元に、クラスカルウォリス検定で使用する確率分布である「カイ二乗分布」を描き、今回の結果である「H値」がカイ二乗分布の中でどの位置にあるのかを点線として表示されます。
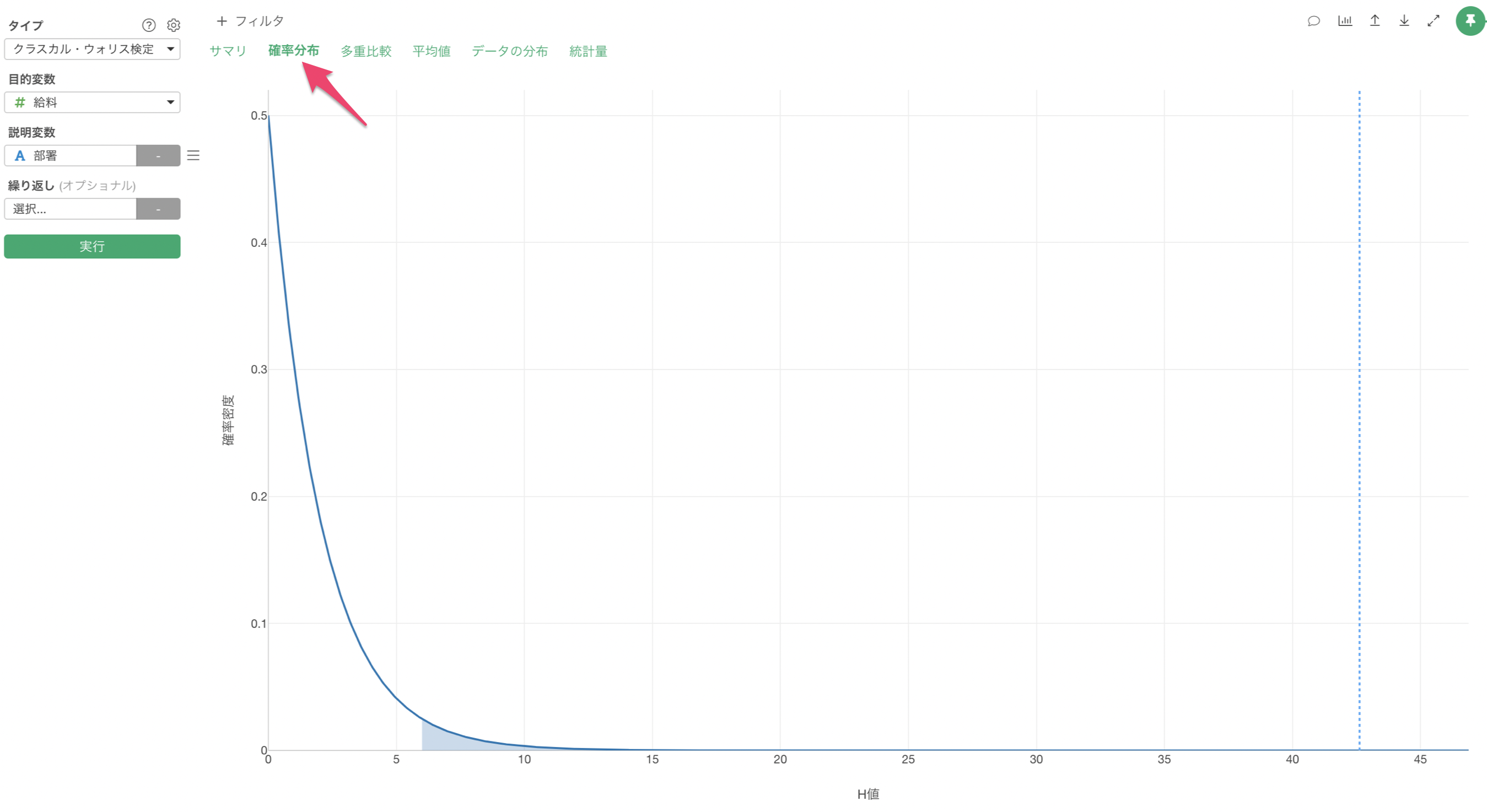
多重比較
クラスカル・ウォリス検定では、「部署」によって「給料」に差があるのかを検定しますが、これだけではどの組み合わせ(例: 営業と研究開発)で有意な違いがあるのかがわかりません。
そこで、「多重比較」のタブでは、どの組み合わせで差が有意となるのかを調べることができます。

クラスカル・ウォリス検定で使用している多重比較の手法は「Dunn's Test with Bonferroni Correction」を使用しています。
もし変更したい場合は、プロパティから変更が可能です。
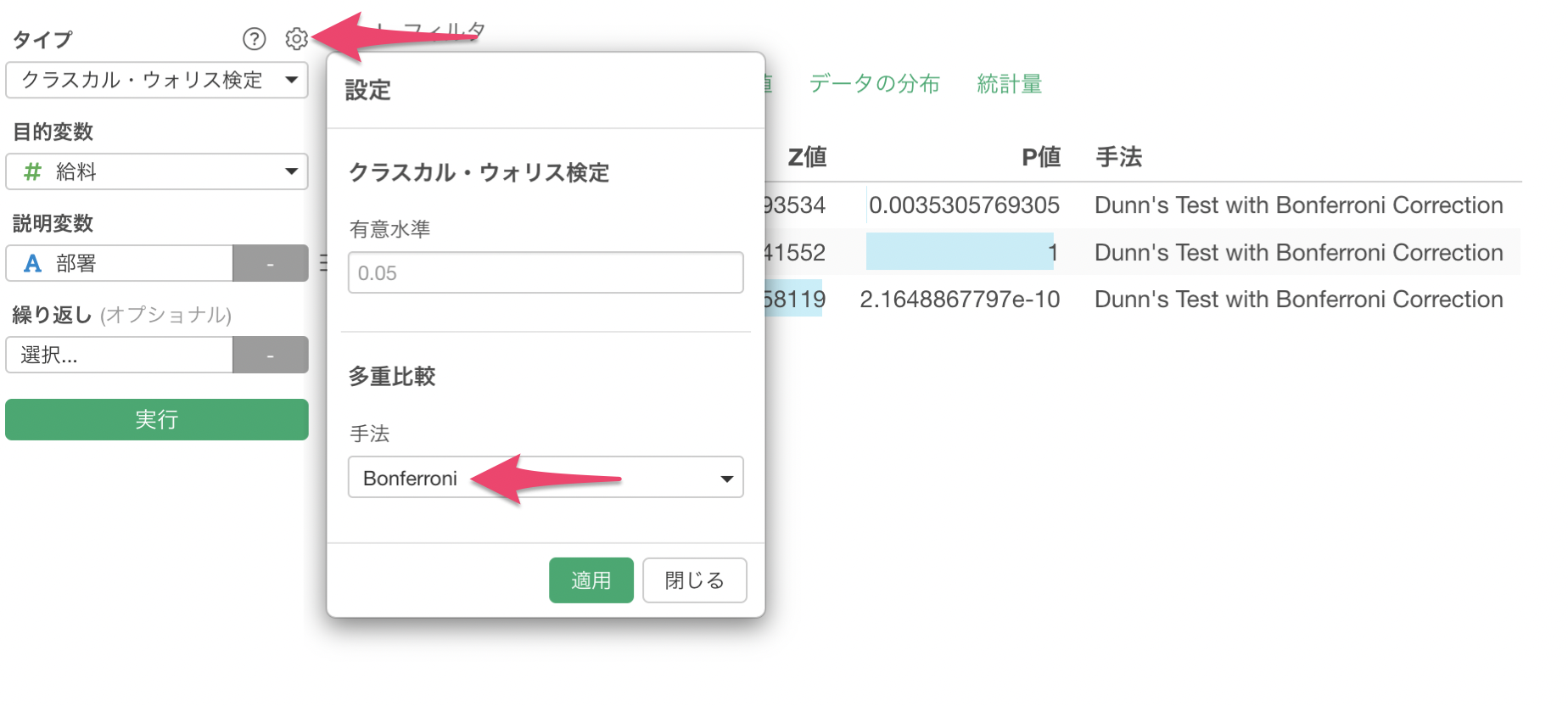
ダン検定(Dunn Test)は、順位をもとにしており、グループでの順位和とその差を標準誤差で割った値が標準正規分布であるZ値となりますが、この値をもとに確率分布に当てはめて検定を行なっています。
平均値
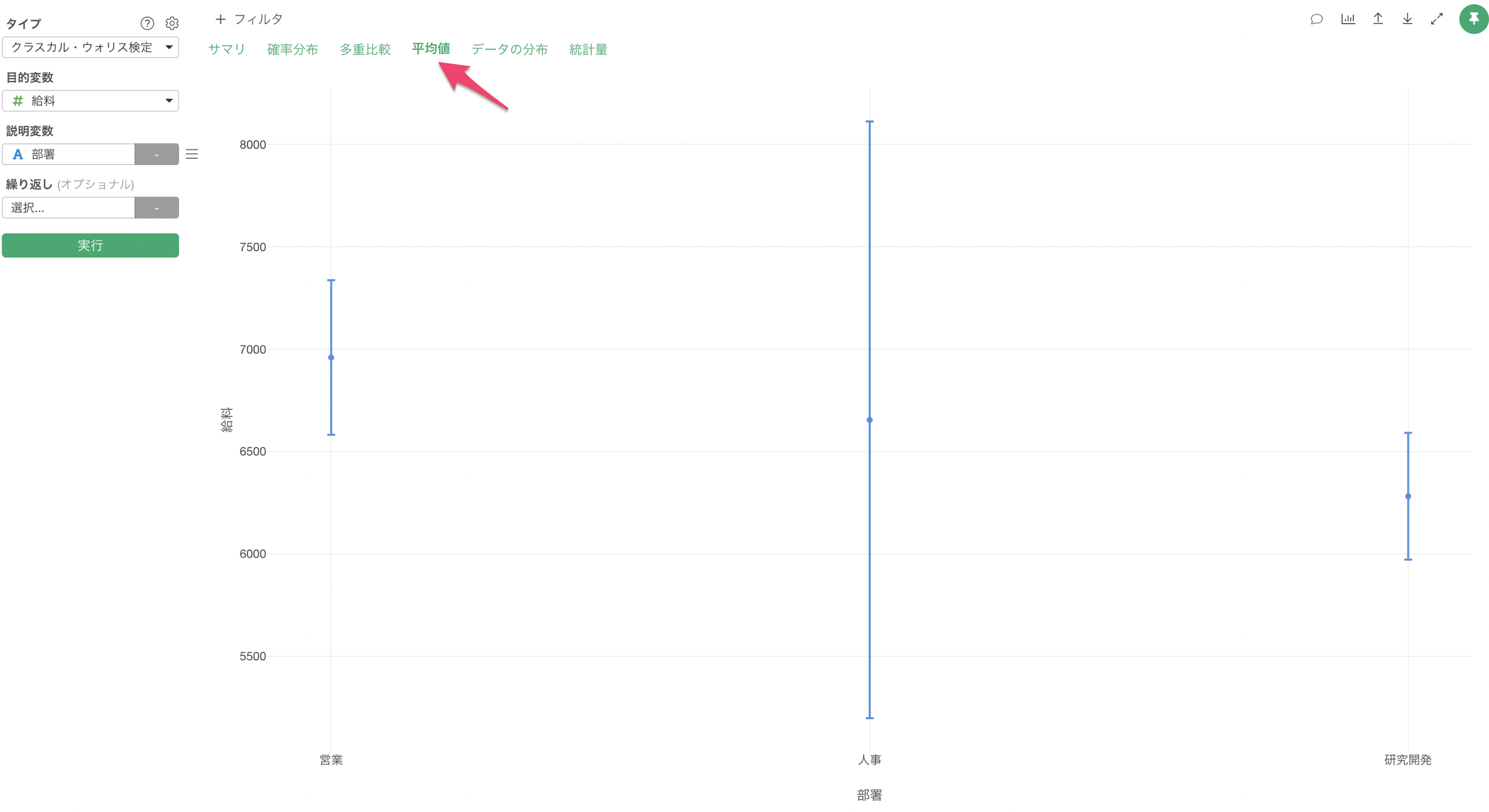
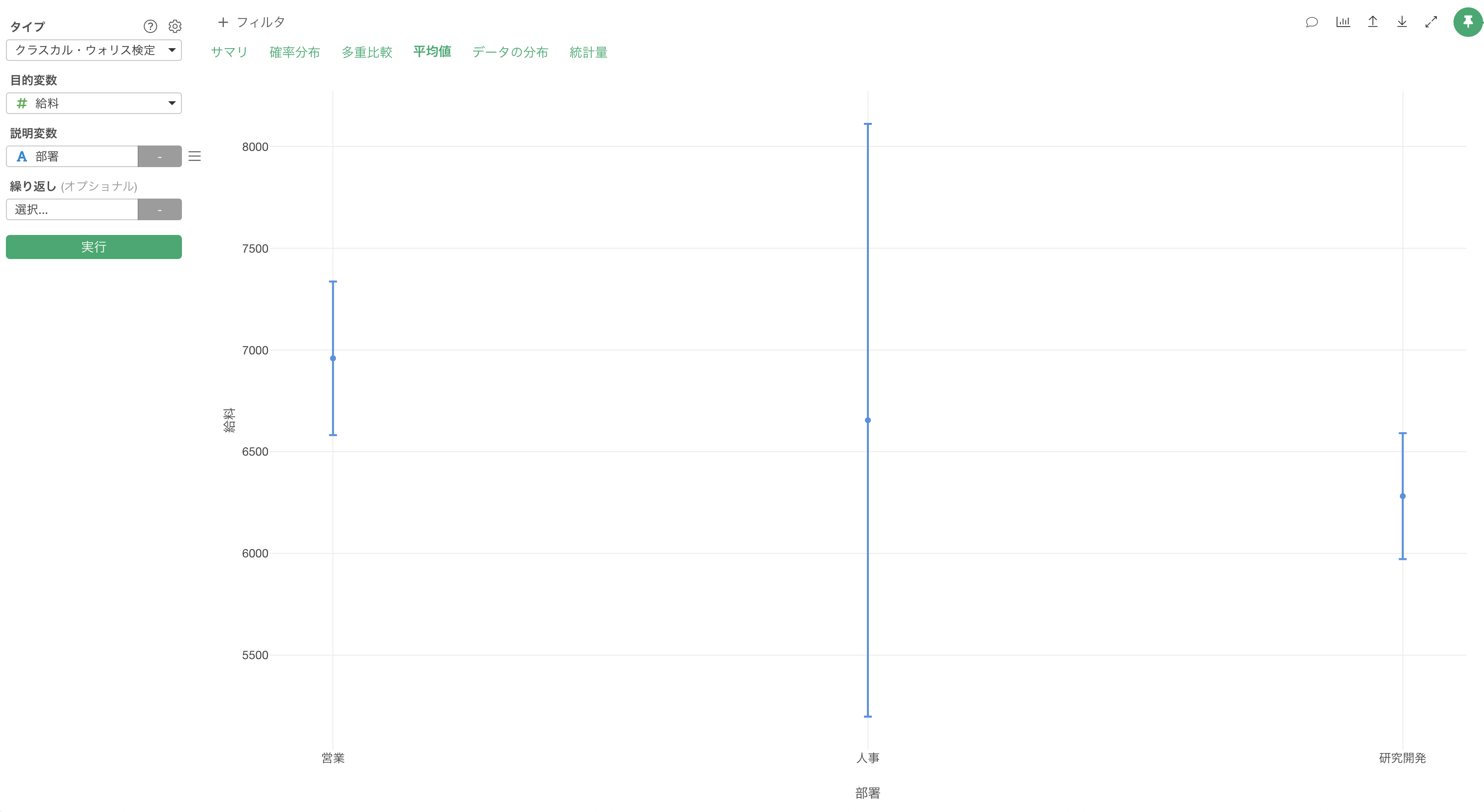
平均値のタブでは、それぞれの部署の平均値と95%信頼区間をエラーバーとして可視化しています。