最初の差を覆す線形回帰のちょっとした傾きの話
今回は、みなさんがこれからのキャリアを考えていく上で最も重要な話を紹介したいと思います。
数多くある予測モデルの中でも最もシンプルで古くから使われている線形回帰を使ったキャリアの構築に関する話です。
これはもともと、私がExploratoryという会社を創業する頃にある知人が紹介してくれた、スタンフォード大学の教授によるコンピューターサイエンスのクラスの生徒に向けた話で(リンク)、どう自分の専門となるスキルを伸ばしていくか、さらにどういう人を雇っていけばよいのかを考える上で、今でも北極星のように指針を与えてくれるかのような素晴らしい話です。
その話のスクリプトがウェブに公開されていたので、こちらに皆さんと共有したいと思います。(リンク)
以下、翻訳。
みなさんに週末の間にちょっと考えてほしいことがあります。それはちょっとした傾きの差が最初にあった差を覆すということについてです。
こちらのチャートを見てみてください。
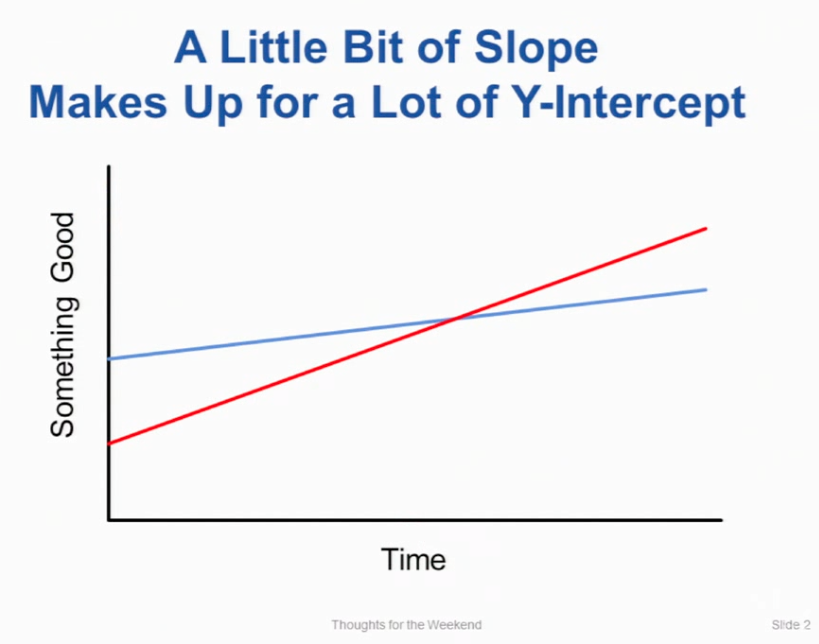
これは数学的には明らかなことですね。
赤と青の2つの直線があります。赤い線は青い線よりも低いところにY切片(Y軸に当たるところ)がありますが、傾きがより大きいため、最終的に青い線をまたいでそれよりも値が大きくなっていきます。
もしX軸が時間、Y軸が「何か良いこと」だとするとたいていの人たちは青の軌道ではなく赤の軌道に乗るようなキャリアを選びますよね。
もちろん、あなたがその二つの線が交差する前に自分は死ぬと思うなら別ですが。(笑)
数学的にはあまりにも当たり前のことです。しかし私はこれを数学的な問題として話しているわけではありません。これはみなさんのこれからの人生にとっての非常に大切な教訓として話しているのです。
というのも、この図は「いかに速く学び続けること」が「どれだけ多くのことを最初に知っているか」ということよりも重要だということを示しているからです。
一般的に多くの人達はいかに多くのことを知っているかを気にしすぎる傾向があります。逆に、どれだけ速く学び続けているかを話す人をあまり見かけることがありません。
これはここにいるみなさんにとって良いニュースです。というのもあなたたちはスタンフォード大学の学生なのでとても速いスピードで学ぶことができる人たちです。これはあなたたちにはとって有利となることです。
それではいくつかの例を出しましょう。
最初の例は、あなたがこれから入っていく業界や仕事についてたとえ全くわかっていなかったとしても、新しいことを試すことを恐れてはいけません。恐れる必要はまったくないのです。
素早く学び続けている限り、いずれ追いつき成功できるようになります。
例えば、新しいクラスが始まって最初の一週目に生徒の間でこんな会話をよく耳にします。
「あの人達はこんなことをすでに知ってるけど、どうやったって私には追いつけるはずがない!」
もしあなたが「こんなことを」をすでに知っている一人であれば、それはあなたにとって悪いニュースです。というのも正直言ってすべての人達はとても速いスピードであなたに追いつきます。気づいたときにはそうした「優位」は消え去っているものです。そして、もしあなたが周りと同じスピードで学び続けていないのであれば、他のみんなの後塵を拝することになるでしょう。
もう一つの例を出しましょう。
それは、たくさんの人たちが彼らの人生の途中で溝にはまってしまうというものです。彼らは自分にとって間違った仕事をしていることに気づきます。間違った仕事、間違った奥さんやだんなさん、何でもいいのですが間違った何かです。
そんなとき、彼らはそこから抜け出し何か新しいことを試すのを恐れます。よくあるのは周りの目を気にしてしまうというやつです。
ところで、奥さんやだんなさんの例は冗談ですが。(笑)
しかし真面目な話、みんな新しいことを試すのを恐がります。周りの人の目を気にしたり、つまらない間違いを犯してしまうのではと心配したりするからです。
しかし、私がここで言いたいのは、とにかくやってみろ、そしてそこからの学びに集中しろ、ということです。
誤解のないように、奥さんやだんなさんの例をこの話から完全に抜いてください。(笑)
仕事に関する話だと思って聞いてください。
もう一つの例は雇用に関してです。
数年前学校に戻ってくる前まで私はスタートアップをやっていました。そこで気づいたのは、みんな過去の経験を元に採用しようとしているということでした。
彼らは採用しようとしている人の履歴書を見て、彼らがやってほしいと思っているような仕事をすでに何度もやっているかどうか確認しようとするのです。
これは基本的には例のチャートで言うところのY切片(それぞれの線がY軸に当たる場所)で採用しようとしていることになります。
私は個人的にこれはあまり良い採用の仕方ではないと思います。
そもそも同じことを何度も何度もやっている人たちはたいてい燃え尽きてしまいますし、そもそも同じことを何度もやっているということはそれが彼らの限界だからでしょう。彼らにはそれ以上のことができないのではないでしょうか。
そこで、私はいつも「適正」、「素質」といったことを見て採用するようにしています。経験ではありません。
この人はほんとうにこの仕事ができるのだろうか?彼らは過去にやったことないし、この領域における経験もないかもしれないけど、自分でどうやったらできるか考え出すことができるという意味でスマートな人だろうか?彼らは素早く学び続けることができるのだろうか?
自分の経験を通して、ほんとうに優れた人を雇うにはこうした採用の仕方のほうが断然良いことに気づいたのです。
この「傾きと切片」はとても興味深いコンセプトで、いろんなことに応用できます。ここで重要なのは、「遅くとも着実に前に進む」ということです。
何か起死回生を狙ってヒーローのふりをする必要はないのです。さらに傾きが特に大きくある必要もありません。毎日少しずつより多くのことを学び、少しずつ改善していき、そうした小さいステップをたくさん重ねていけば、思った以上に素早く追いつき、その分野のほんとうの専門家となれるのです。
私はよく自分に対して質問します。
「今日なにか新しいことを一つ学んだか?」
もちろんあなた達は私よりもずっと若いので、あなたの「傾き」はわたしのものよりも大きいでしょうから一日一つと言わず、二つ三つ、または四つと学んでいけるでしょう。
もしあなたが、どこから始まったかを心配するのではなく、自分の傾きがどうなのかをいつも気にしていれば、あなたはいずれ素晴らしい場所に到達できるでしょう。
以上です。
あとがき
何かの専門家、または職人のようにスキルを極めたいというのであれば、周りに流されず毎日その分野のことを学び、練習していくというのは、日本人にとっては当たり前のことであると思います。
イチロー選手のように、ホームランをガンガン飛ばすが故障で消えていく選手を尻目に最後は日米野球史に残るほどの偉大な選手となっていくのはいい例ではないかと思います。
しかし、それでもこうした話というのはまれで、たまに聞くと「やっぱり、そうだよなー」とまるで他人事のように感じてしまうことはないでしょうか?
理屈的にはわかるのだができない、という人は多いのではないでしょうか。
毎日自分にできることをコツコツとやる、というのと毎日自分を伸ばすために後もう一歩余計にやる、という違いが大きのではないかと思います。
そして、この余計な一歩というのが、今回の線形回帰の直線の傾きが平ではなく、右上に向かっていくことを確実にしてくれるのです。
例え同じ料理を作るでも、毎日知ってる料理をするのではなく、新しい料理を学び、新しい料理を試す、その試したことから学ぶというのを毎日繰り返していくことで、直線が上に上がっていくのだと思います。
そして、今回はわかりやすくするために直線を使っての話でしたが、学び、練習、試行錯誤を繰り返すことによってもたらされる成果というのは、時間に対して直線的に同じ傾きで大きくなると言うよりも、実際には指数関数的に大きくなるのではないかと思います。
そもそもこうした努力を積み重ねていくことができる人はほんとに一部の人達だけです。普通は途中で疲れたり、他のことが気になってしまったりして、休んでしまうものです。
そこで、やり続けた人たちというのはもうそのことだけで希少価値があるわけです。そして世の中というのは、そうした希少価値に対してより多くの対価を払うものなのです。
これから新しいことをやってみたいけど、今さらかなとか、自分は向いてないとか、自分はそんな事ができるようにはならないなどと、自分の可能性を自分で制限してしまうのではなく、何でも学び続ければ、余計な一歩をやり続ければ、どんな道でも一流になれると信じて、ぜひ新しいことにチャレンジしてみてください。
以上。
データサイエンス・ブートキャンプ・トレーニング

データサイエンス、統計の手法、データ分析を1から体系的に学ぶことで、ビジネスの現場で使える実践的なスキルを身につけたいという方は、ぜひこの機会に参加をご検討ください!
ビジネスのデータ分析だけでなく、日常生活やキャリア構築にも役立つデータリテラシー、そして「よりよい意思決定」をしていくために必要になるデータをもとにした科学的思考もいっしょに身につけていただけるトレーニングとなっています。