Exploratoryのアナリティクス・ビューを使って様々な角度からクラスターの特徴を理解してみる
K-Meansクラスタリングのアルゴリズムはデータの中にあるカテゴリー同士の類似性や関係を理解したいときに便利です。
よく使われるのは、カスタマーを彼らの購買履歴や興味の対象などといった属性をもとにいくつかのグループに分けることで、それぞれのグループに対してより効果的なアプローチをとるといったユースケースなどがあります。
もちろんカスタマーだけでなく、製品、国など、自分の興味の対象をデータをもとにいくつかのグループに分けたいという時によく使われるアルゴリズムです。
ちなみに、このグループのことをクラスターと呼びます。
クラスタリングを行うアルゴリズムは実はいくつかあるのですが、その中でもよく使われるものの1つにK-Meansクラスタリングというものがあります。
これはExploratoryの中でもデータラングリングのコマンドとして、結構前からサポートされていて、列ヘッダーメニューから簡単に実行することができます。
使い方は比較的簡単で、属性となる列を指定すると、そのデータをもとにいくつかのクラスターに分けてくれます。以下は、2016年のカリフォルニアでの住民投票で17つほどあった法案に対する投票結果をもとに、それぞれの郡(例、サンフランシスコ、サンホゼ、ロサンゼルス、など)を3つのクラスターに分けてみた結果です。
ところが、実はここで多くの人にとっての2つの大きな問題があります。
1つ目は、それぞれのクラスターの特徴は何なのかという問題で、2つ目はそもそもクラスターの数をいったいいくつにすればよいのかという問題です。
そこで、Exploratory v5.0からこうした問題を解決するために、このK-Meansクラスタリングのアルゴリズムをアナリティクス・ビューでも使えるようにしました。
このポストでは、アナリティクス・ビューを使って、クラスタリングの結果を様々な角度から可視化していくことで、それぞれのクラスターの特徴を理解する方法を紹介します。
最適なクラスターの数の探し方については、以下のポストを参照してください。
データ
こちらに先に紹介した、2016年のカリフォルニアでの住民投票の投票結果を郡ごとに集計したデータがあります。
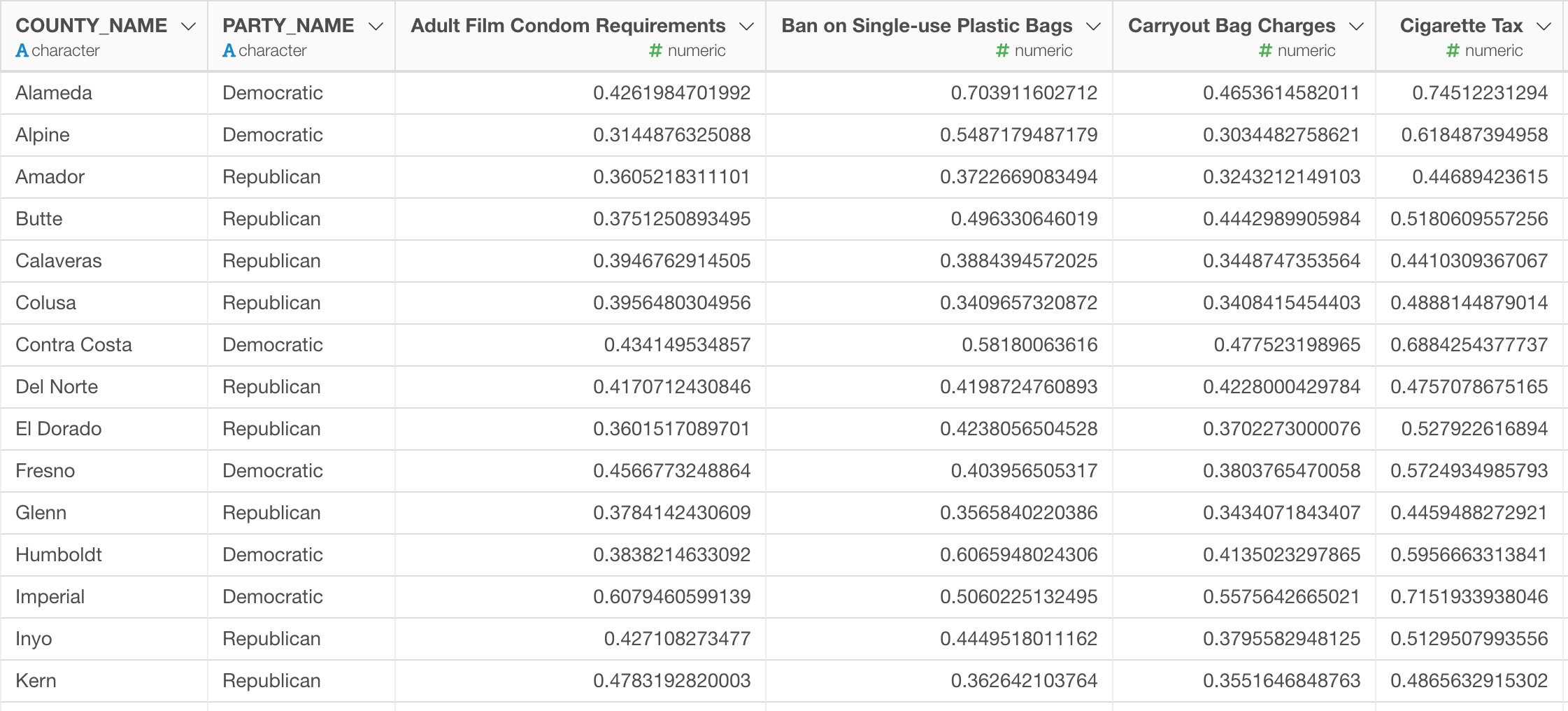
17つの法案が投票にかけられたのですが、さすがカリフォルニアだけあって、結構ワイルドな法案が多いです。(笑)例えば、マリワナ(大麻)の合法化、アダルトビデオでのコンドームの着用の義務化、銃の販売をきびしくするかどうか、など17つほどあります。
それらに対する投票結果を58ある郡ごとに集計し、賛成した人の比率を支持率として出しています。
下のチャートはX軸にそれぞれの法案の名前、Y軸が賛成した人の割合、それぞれの点がそれぞれの群を表しています。
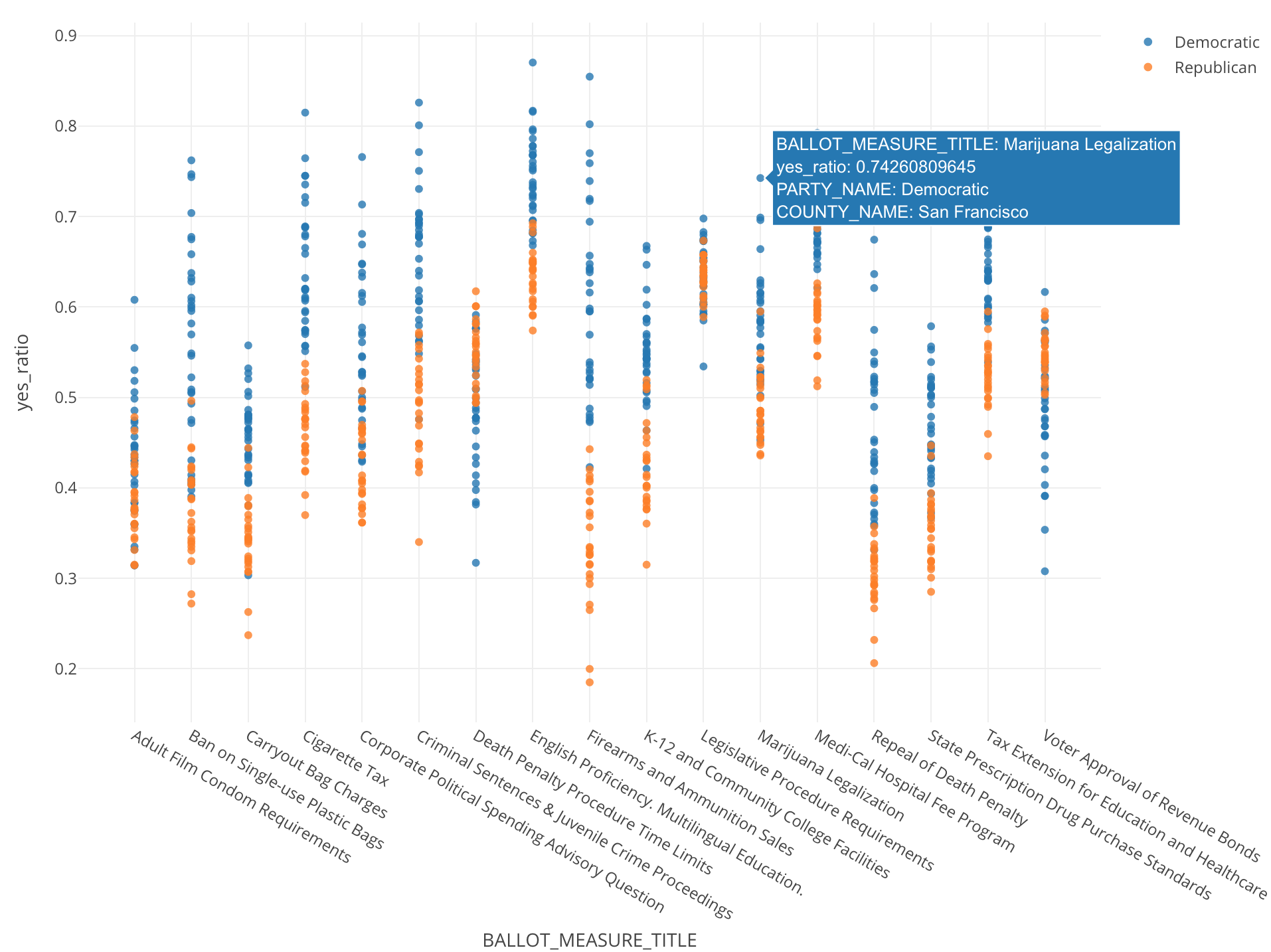
さらに色はその時に同時に行われていた大統領選挙での結果をもとに、それぞれの群が全体として共和党(トランプ)よりなのか、それとも民主党(ヒラリー)よりなのかを表しています。
これを見ると、例えばサンフランシスコはマリワナの合法化に対して74%の支持率だったということがわかります。
K-Meansクラスタリングをデータラングリングのステップとして実行する
まずは最初に、K-Meansクラスタリングをデータラングリングのステップとして実行し、その結果をチャート・ビューで可視化してみましょう。
先ほどのデータを使って、それぞれの郡を17つの法案への支持率をもとにいくつかのクラスターに分けてみましょう。
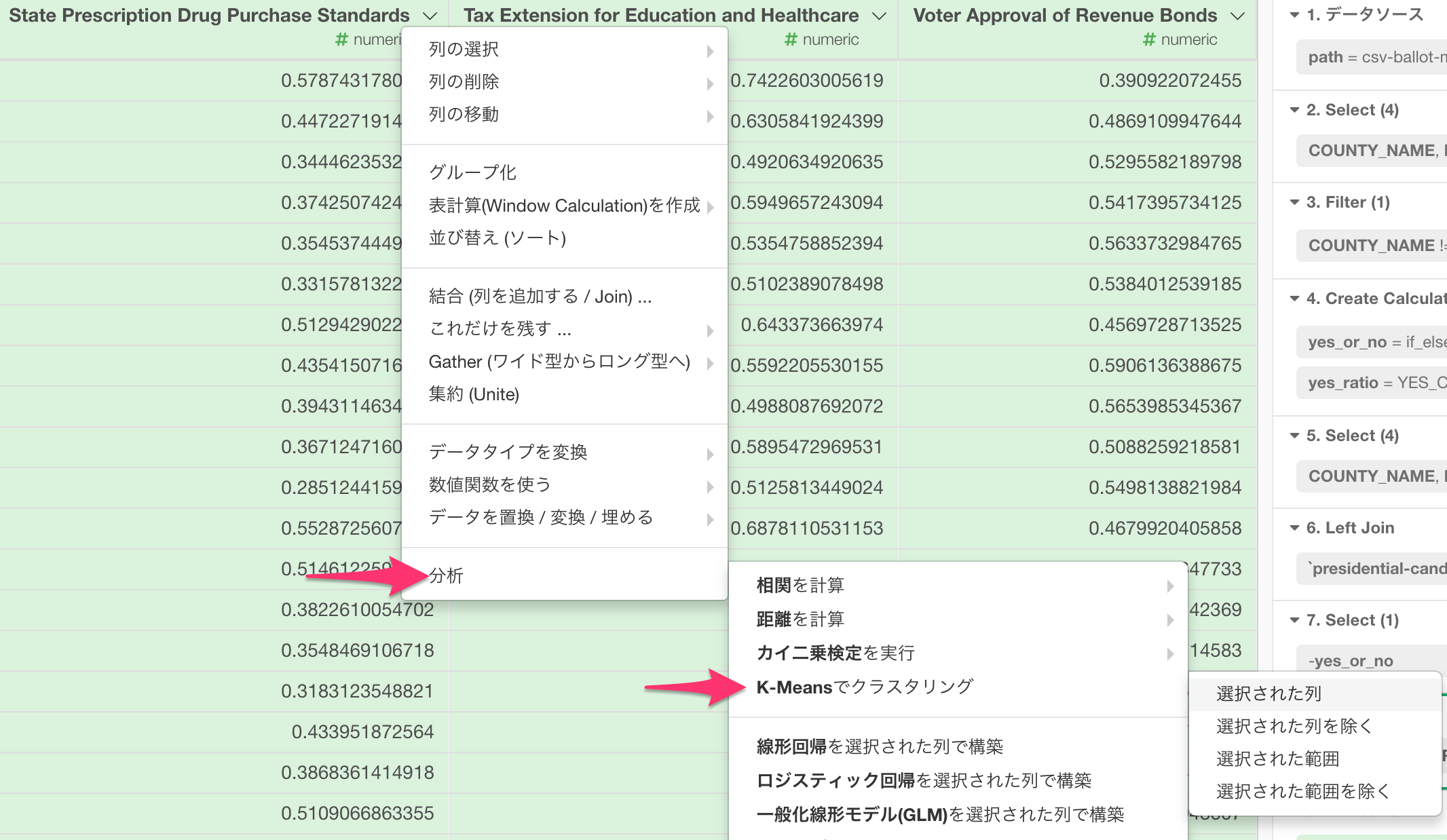
17つの法案に対応する列をShiftキーを使って全て選び、列ヘッダー・メニューから、
分析 -> K-Meansでクラスタリング -> 選択された列
を選びます。

すると、新しいclusterという列ができそこにそれぞれの郡に対するクラスターのIDが振られているのが確認できます。
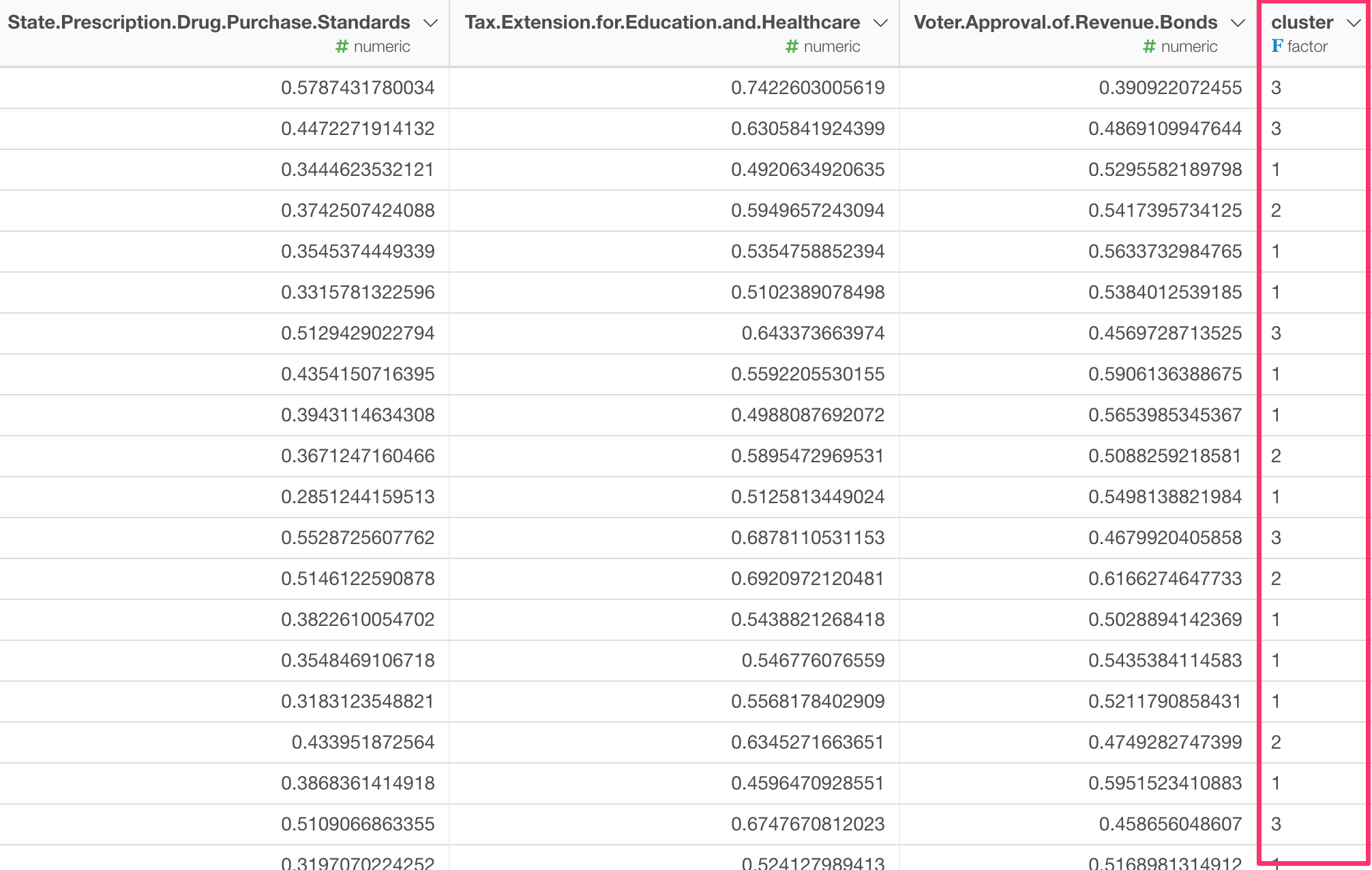
一度このクラスター分けができれば、あとはこの結果をチャート・ビューで可視化できます。
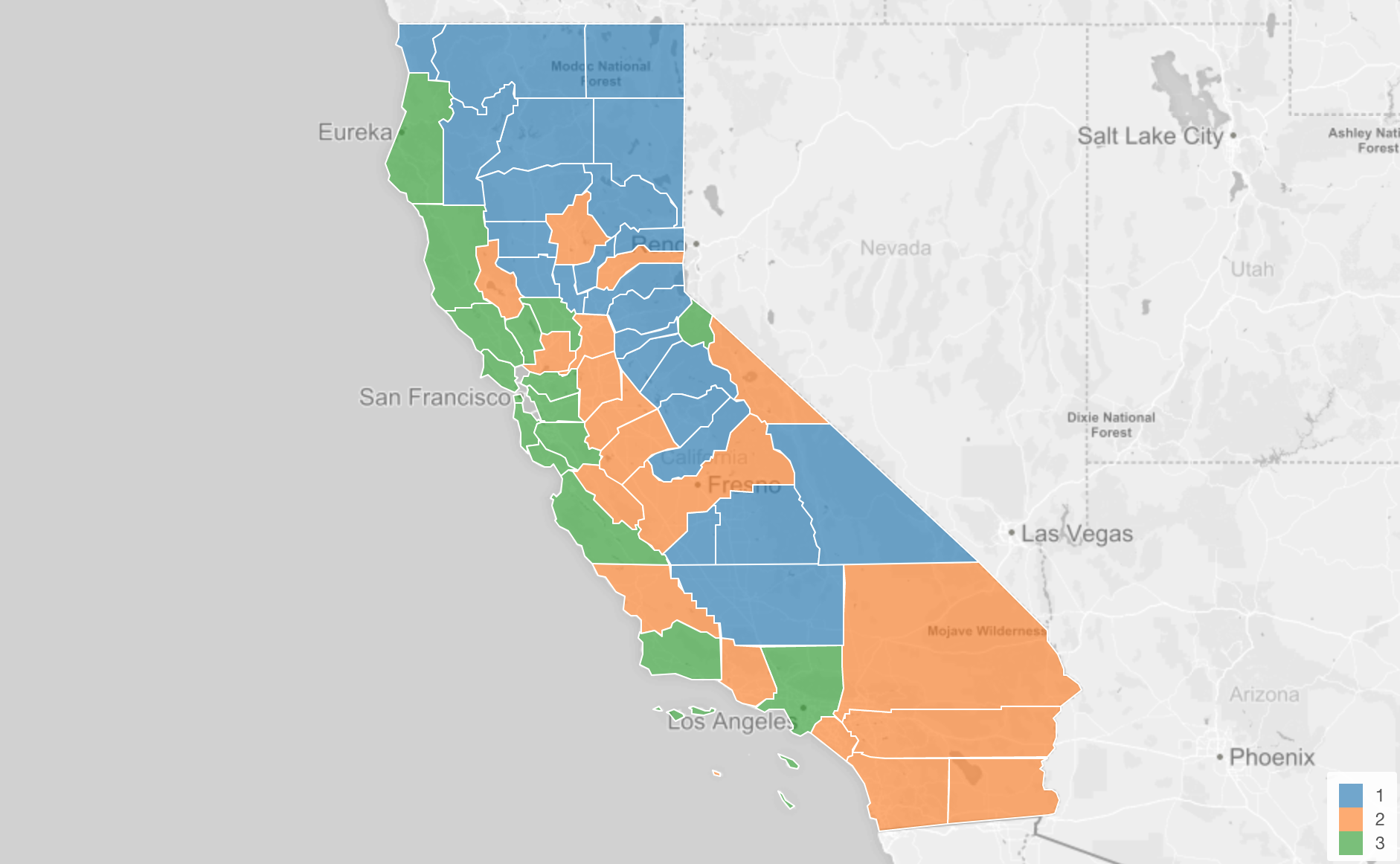
先ほども見ましたが、こちらは地図上にそれぞれの郡をクラスターごとに別の色を使って表したものです。
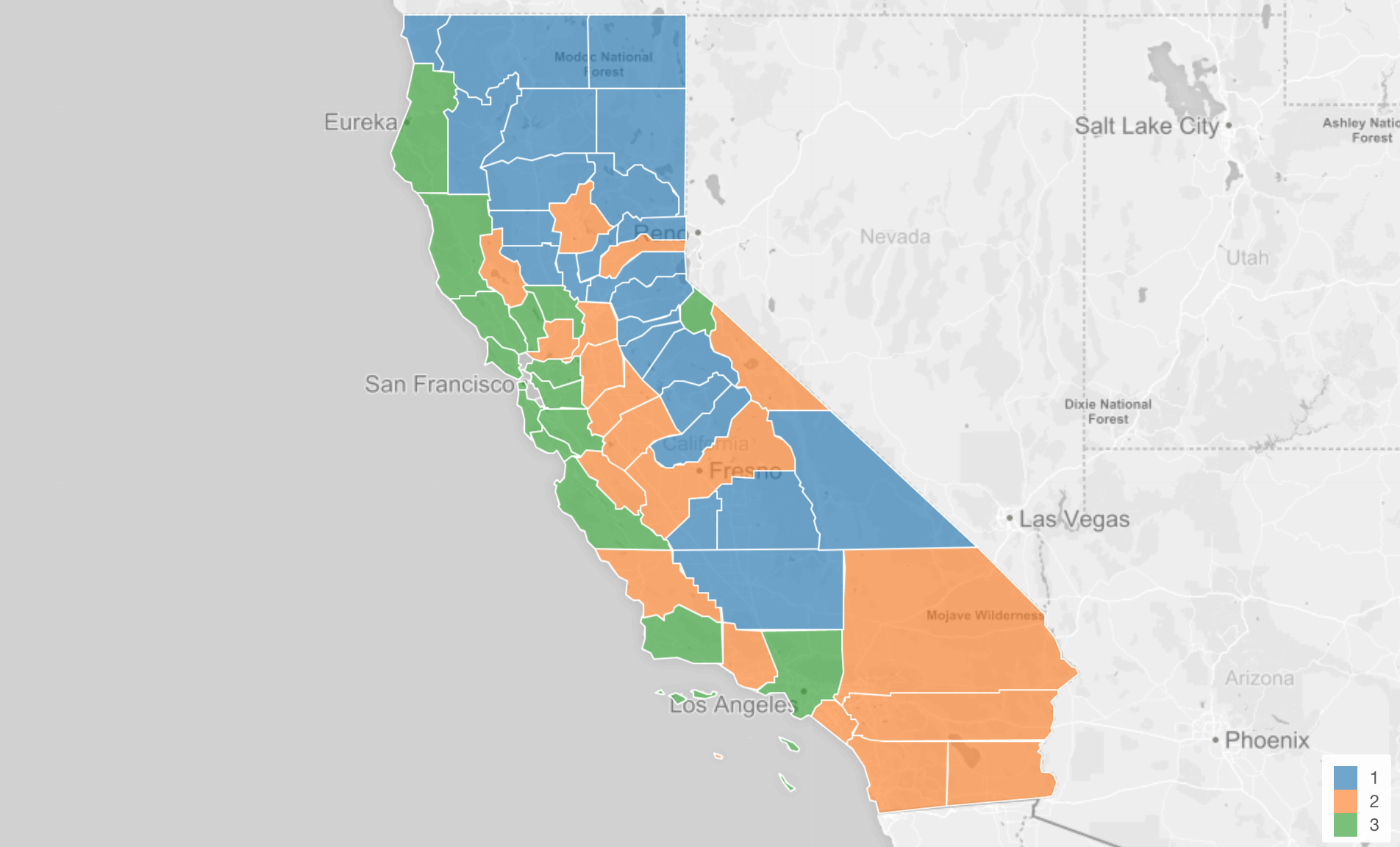
さてここで、わたしたちが知りたいのは、それぞれのクラスターにはどういう特徴があるかです。この地図を見ると海岸沿いにある郡は緑色のクラスター3となっていますが、このクラスターにはどういった特徴があるのでしょうか。例えば、マリワナの合法化に関して他の青やオレンジのクラスターに比べて、より強く賛成した郡の集まりなのでしょうか。
この質問の答をアナリティクス・ビューを使って探していってみましょう。
K-Meansクラスタリングをアナリティクス・ビューで使う
それでは、さっそくアナリティクス・ビューに行き、「K-Meansクラスタリング」を選びます。
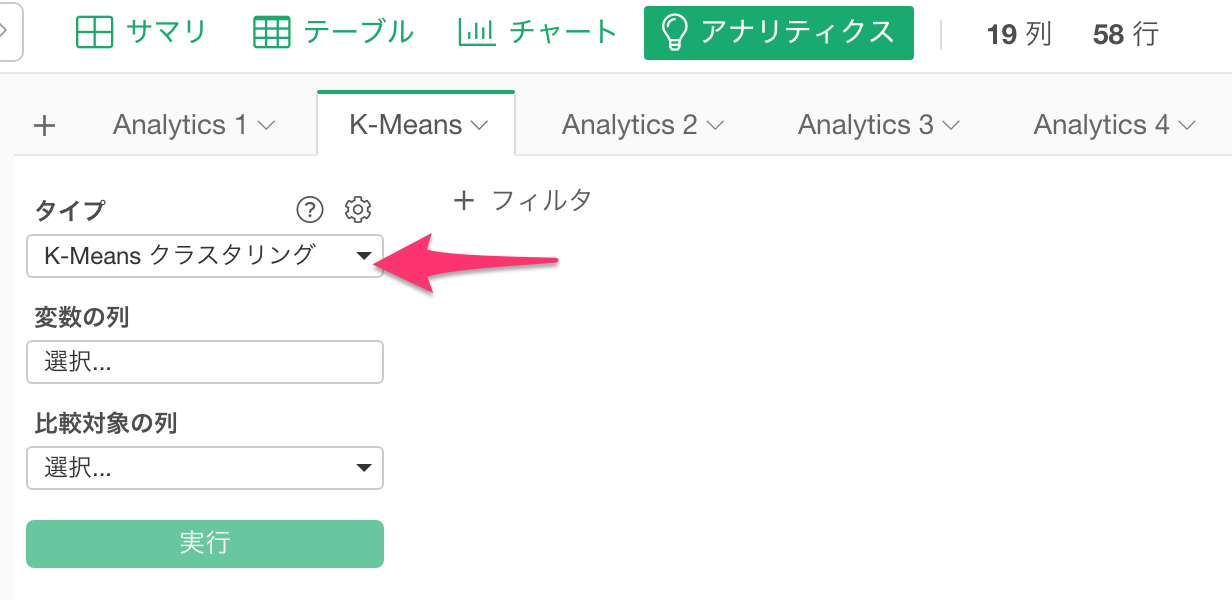
次に、「変数の列」をクリックして、法案の列を全て最初から最後までShiftキーを押しながら選びます。
選べたら、「実行」ボタンを押します。
すると、すでに定義されているいくつかのチャートが生成されます。これらのチャートを使って、それぞれのクラスターの特徴を見ていきます。
散布図
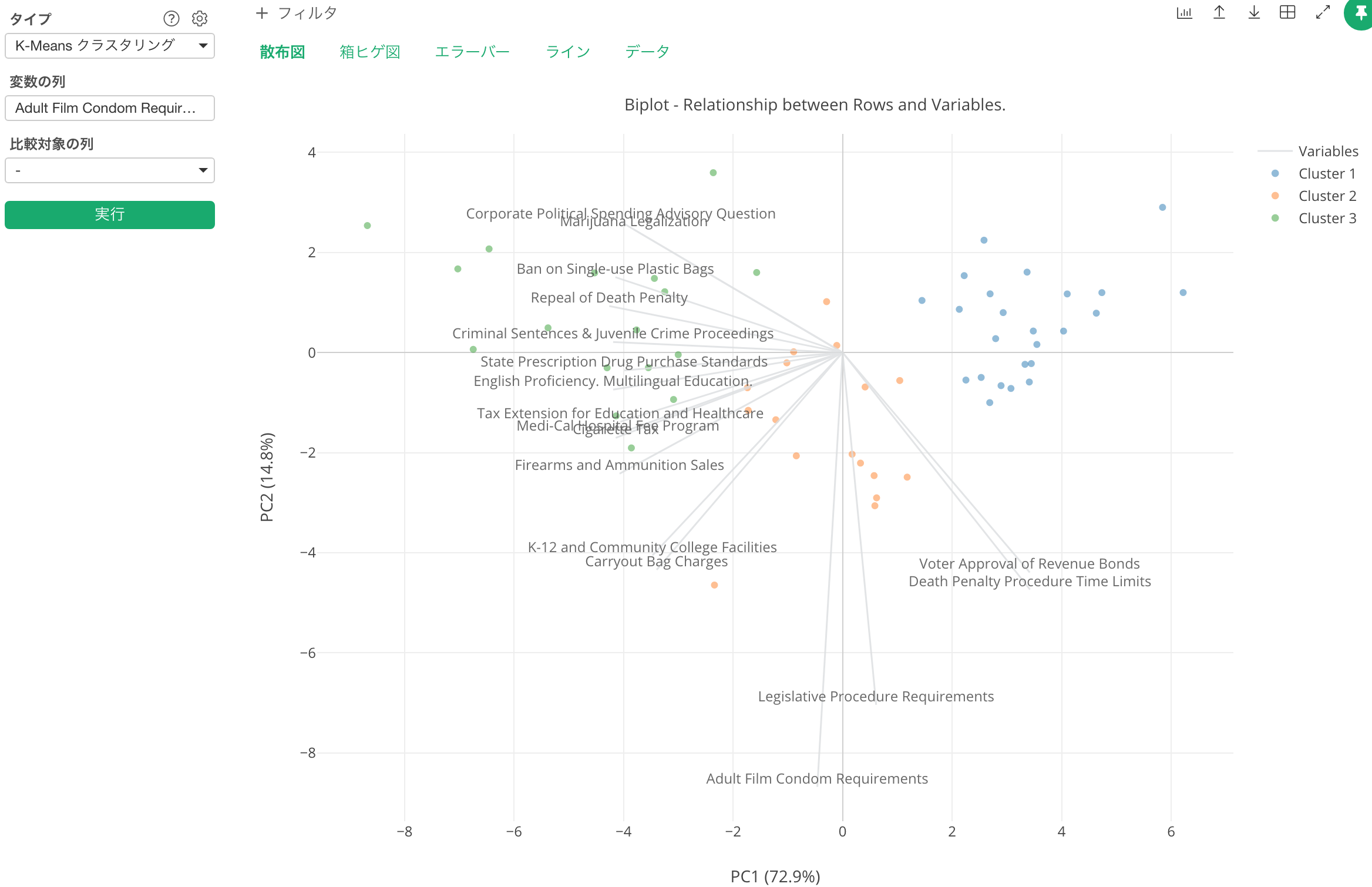
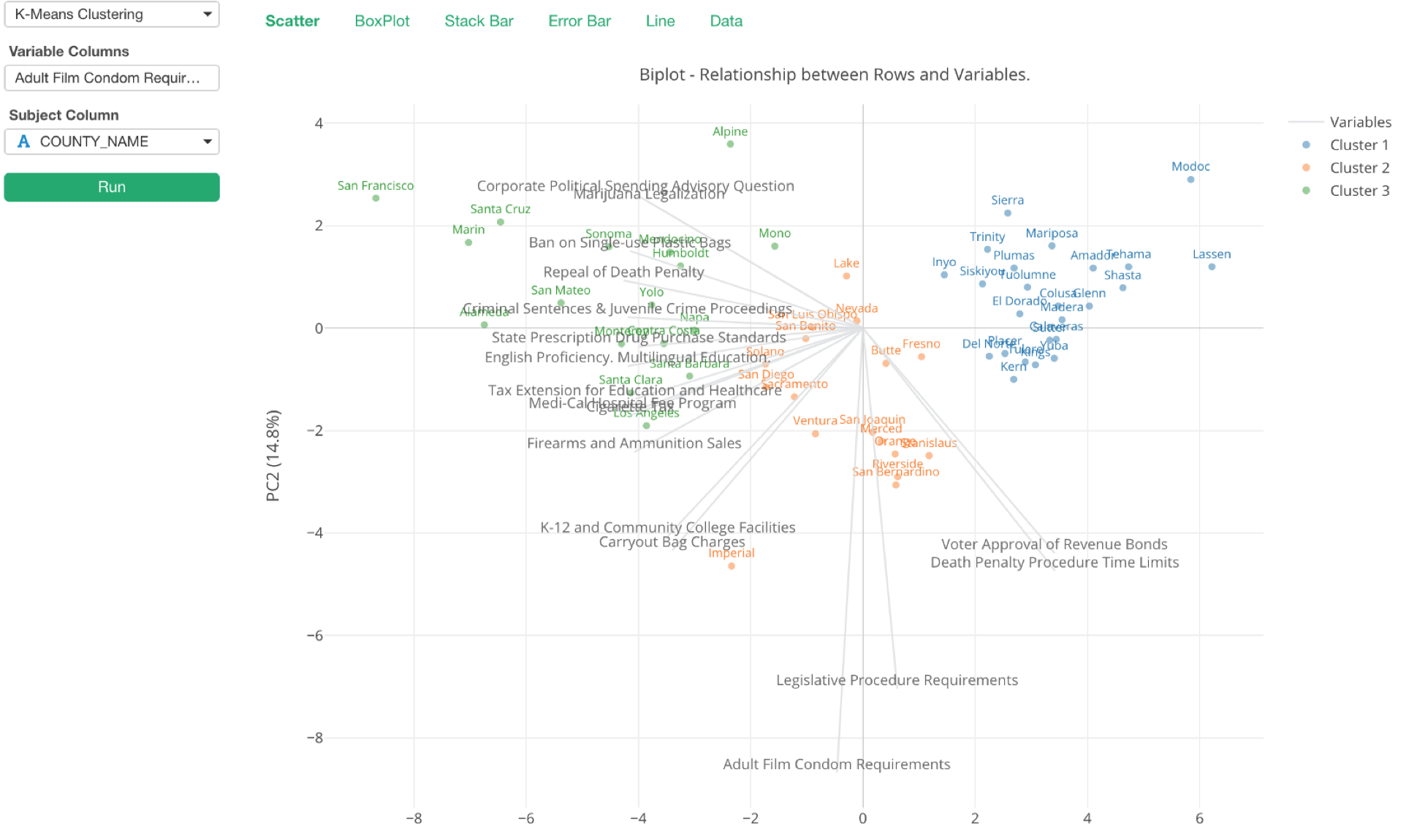
ここに出ているチャートは、業界用語では「バイプロット」と呼ばれているものですが、裏にある理論は少し複雑ですが、結果の解釈の仕方は比較的シンプルです。
それぞれの行(ここでは郡です)が点となってXとYという2つの軸によるエリアに表示されています。このXとYというのは、簡単に言うと、PCA(Primary Component Analysis / 主成分分析)というアルゴリズムを使って17つある法案の列である変数を、もともとの情報をなるべく失うことなく、2つの列で表そうとするとできあがるものです。ちなみにこういうのを、データサイエンスの世界では次元削減と呼びます。
さらに、グレーの線がたくさん中心から放射状に出ていますが、それぞれはもともとの17つの法案で、それらがさきほどのXとYという2つの軸によるエリアではどういうふうに表されるかというのがわかります。
最後に、それぞれの点の色はクラスターのIDを表しています。現在は3つのクラスターに分かれています。
それでは、これをどう解釈するか、以下の矢印で示されている点をもとにみてみましょう。
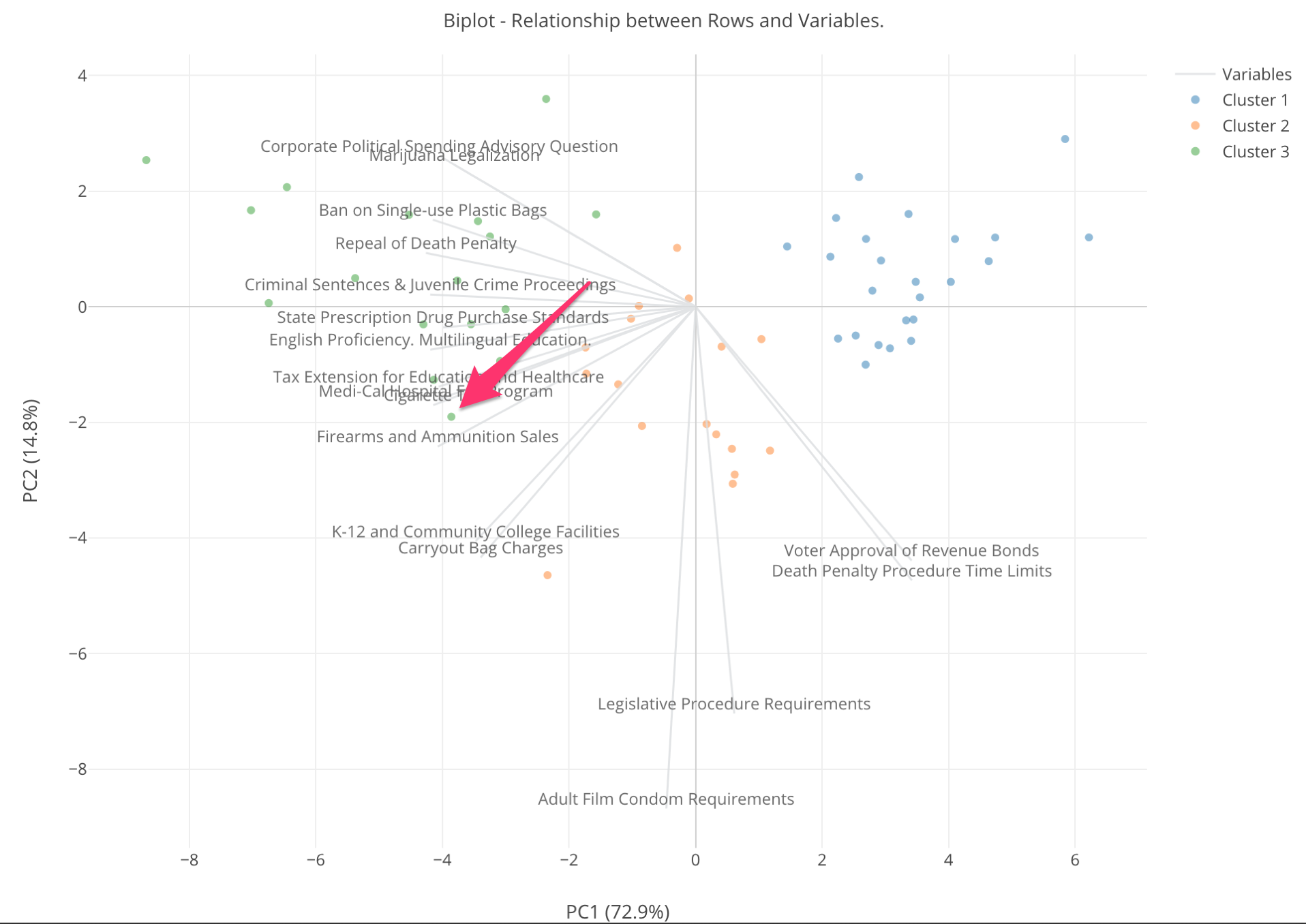
この点は緑なので、これはクラスター3に分けられた群だということがわかります。そして、その近くに、「Firearms and Ammunition Sales」という線がありますが、これはこの郡がこの変数に対して高い数字を持っているということを意味します。つまり、この郡はこの「銃を買うのを難しくしよう」という法案に対して高い支持率を持っているということになります。
この「Firearms and Ammunition Sales」という線に近く、さらにその一番先に近ければ近いほど、その付近にある郡は支持率が高いということです。
逆に、この線の反対側、つまり0を超えた向う側にあるということはそれとは逆の動き、つまりこの法案に対しての反対度が高いということになります。つまり、以下のチャートの赤い線の付近にあり、さらに線の端の方にある郡は、この法案に対する反対度が高いといえます。
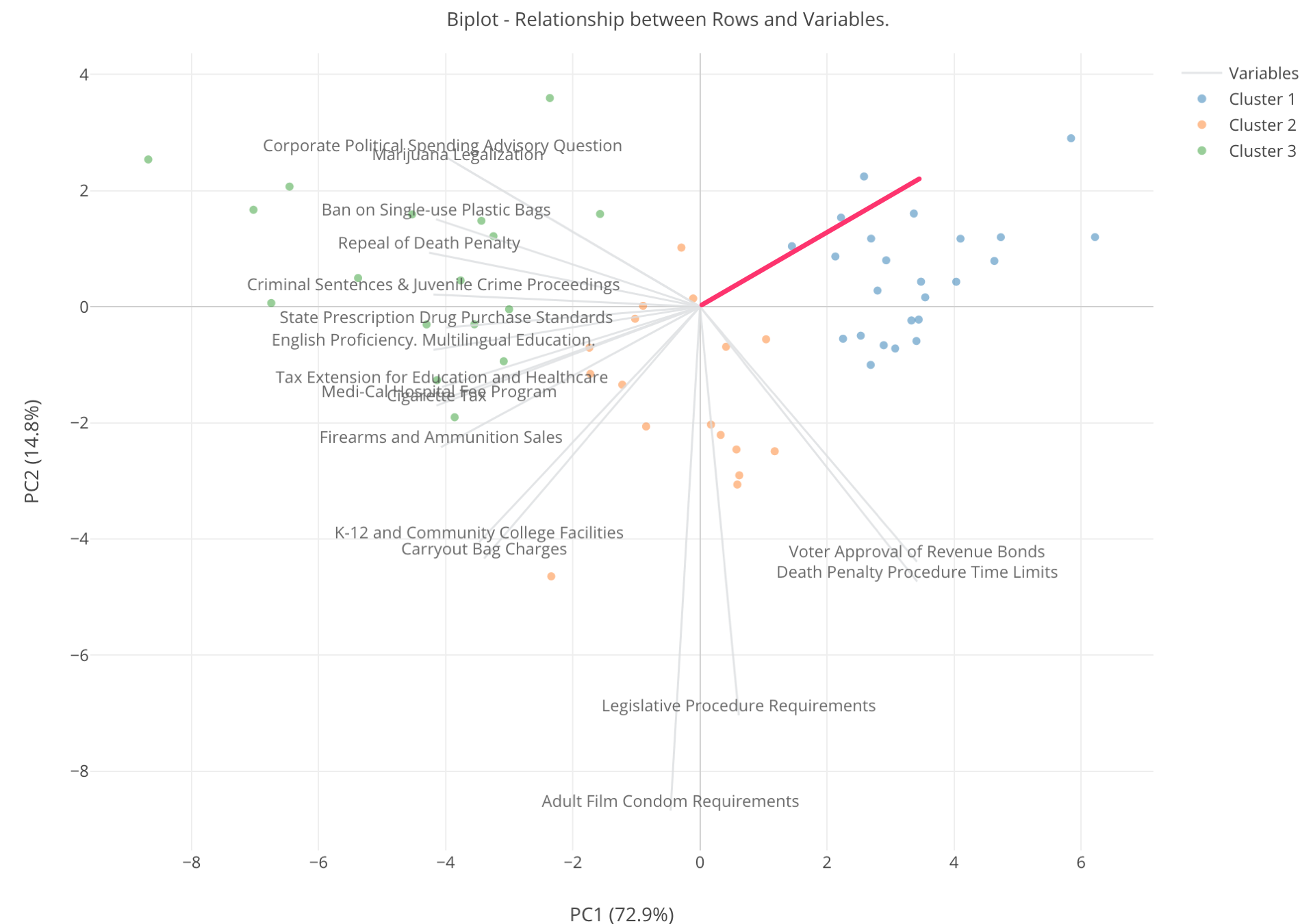
色を見ると、緑の郡は左側に偏っていて、青い郡は右側に偏っています。そしてその中間にあるのがオレンジの郡です。ということは、緑色のクラスターはそこに近いグレーの線で表されている法案への支持率が高い郡の集まり、逆にそれらの法案への支持率が低いのが青いクラスターであるようです。オレンジはどの法案に対してもあまり大きく賛成したり、反対したりすることのない郡の集まりとも言えるでしょう。
ポルノ女優のことが気になってしょうがないインペリアル郡の人たち
ここで、Y軸に沿って下に伸びている、「Adult Film Condom Requirements」という法案への支持率を表すグレーの線に注目してください。オレンジのクラスターにある一部の郡はこの法案に対する支持率が比較的高いようです。逆に、さきほどの緑と青のクラスターに属する郡にとっては、こうした法案に対する関心はあまりないのか、そこまで高い賛成も反対も示していないようです。
これだけでは、それぞれの点が一体何を意味するのかがわからないので、ここで、「比較対象の列」に群の名前が入っているCOUNTY_NAMEという列をアサインして、もう一度実行してみましょう。
するとマウスを点の上に持っていくと、それぞれの点がどの郡なのかがわかります。
例えば以下のオレンジの郡はImperialという群ですが、この郡にとってはアダルトビデオでコンドームを着用するかどうかというのは重要なようです。
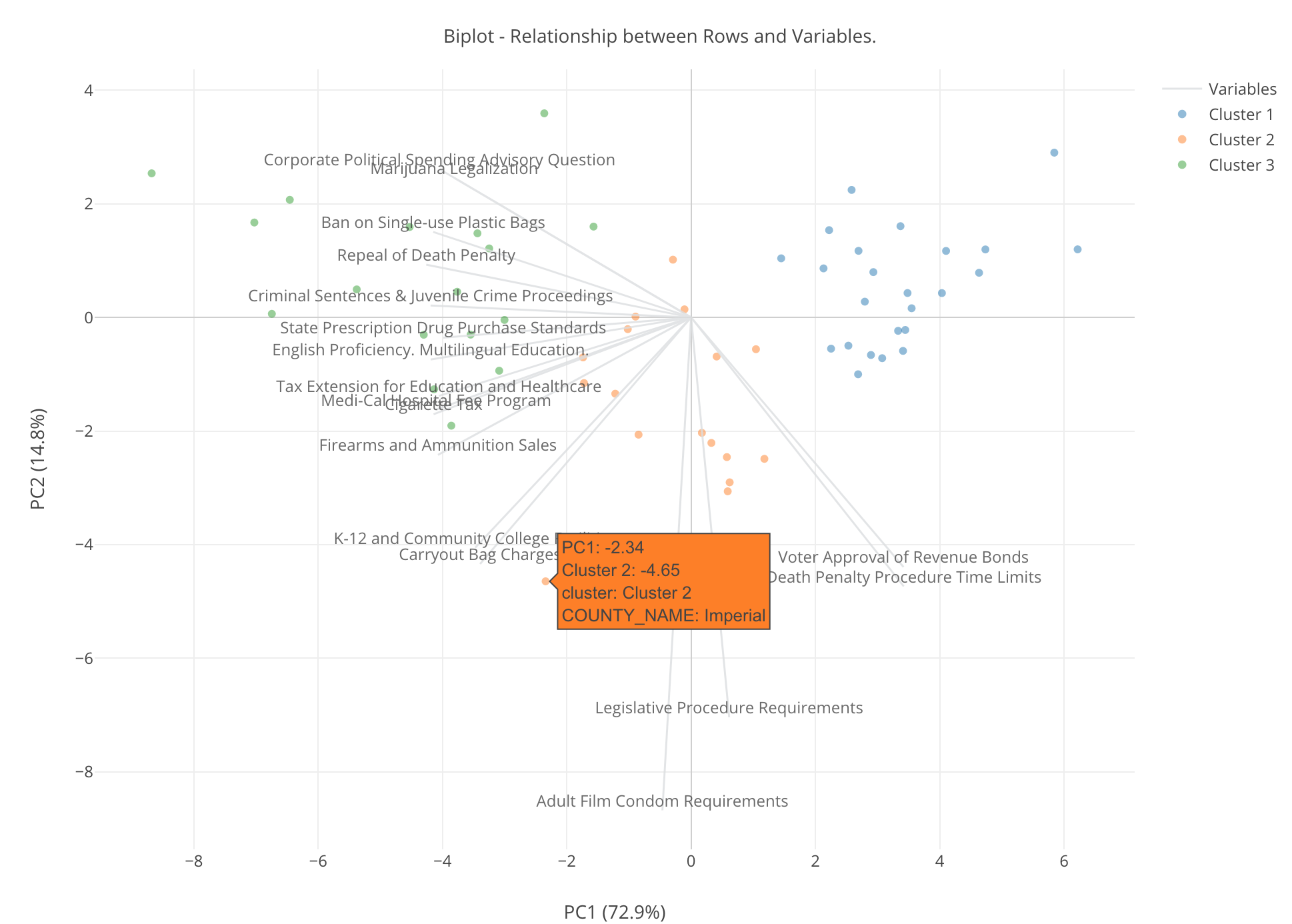
どれくらい重要なのかは先ほどみたこちらのチャートからわかります。
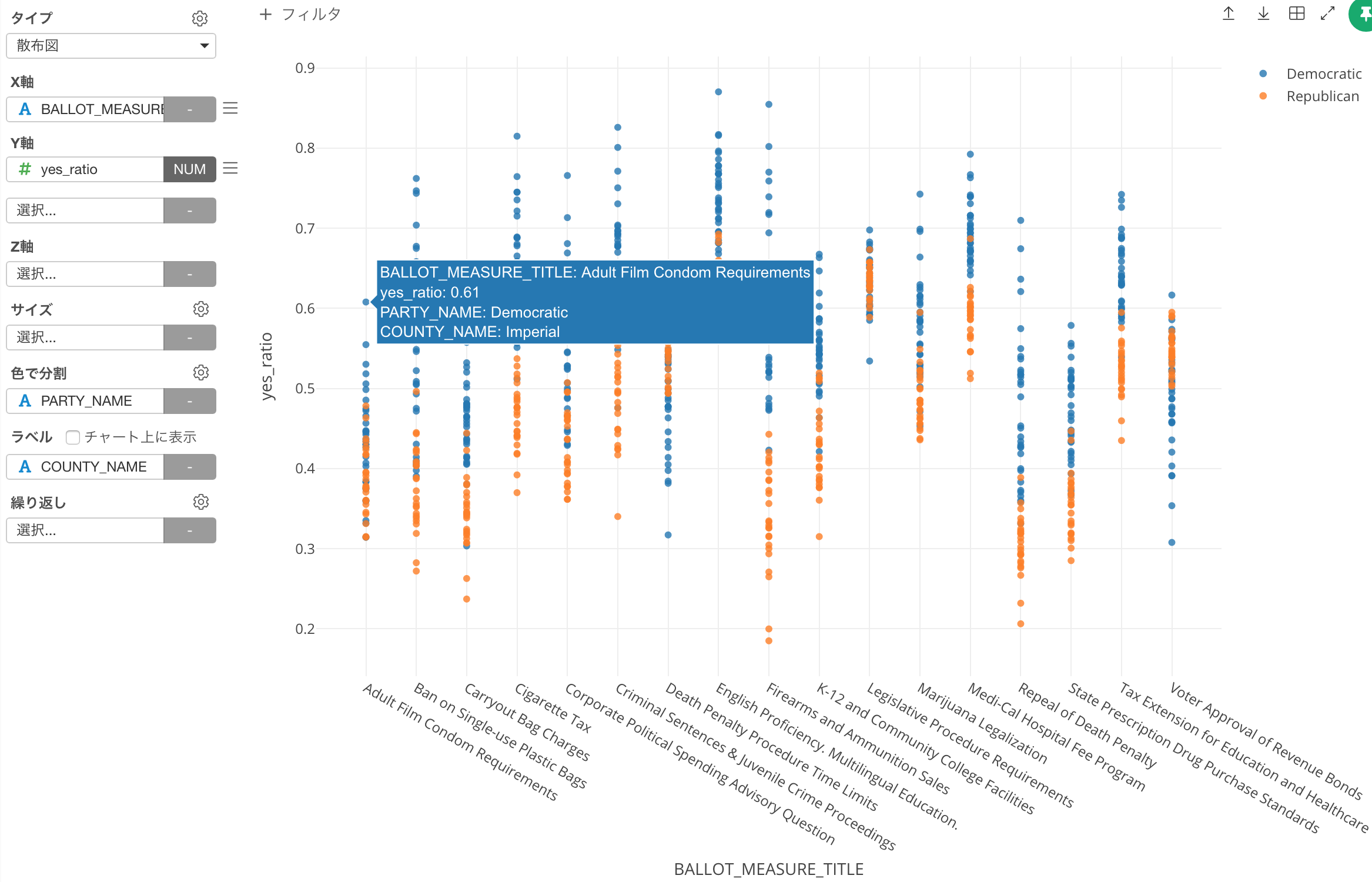
支持率じたいはそんなに高いわけではないですが、それでも他の郡に比べると頭が1つでているといったかんじです。
4人に1人がマリワナの合法化に賛成する圧倒的にリベラルなサンフランシスコ
それでは、もう一度さきほどのバイプロットのチャートに戻りましょう。
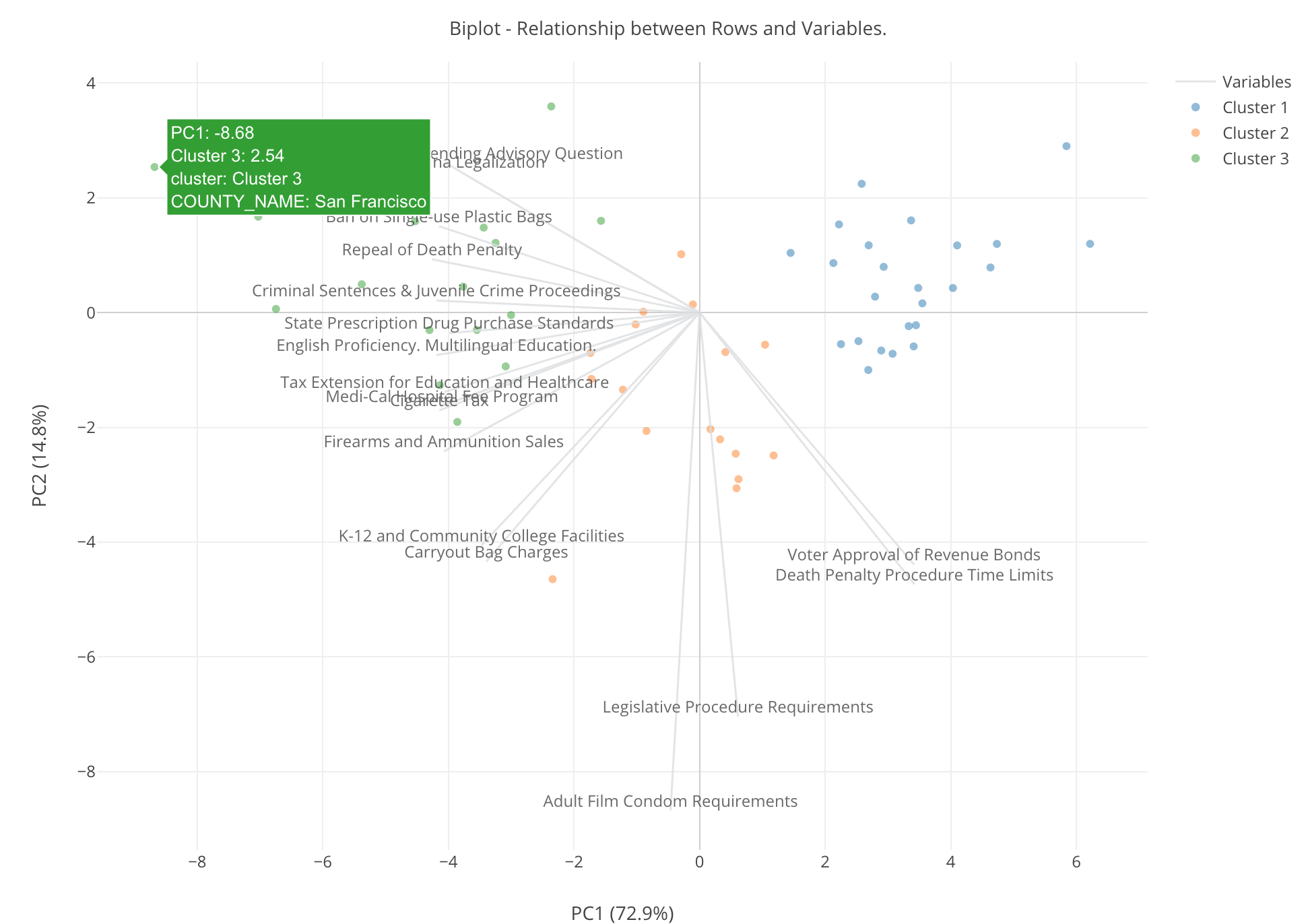
ここで、一番左の端の方に位置している郡はサンフランシスコです。
これはこちらの方向に伸びている法案に対する支持率が高いということです。実はこのあたりにある法案はリベラルな法案ですのでそれらに対する支持率が高いということで、それはかなりリベラルな郡ということになります。ここからわかるのは、リベラルな緑のクラスターの中でもサンフランシスコは筆頭でリベラルであるということが言えます。
実は先ほどのチャートでもサンフランシスコはリベラルな法案に対してただ賛成が多いというだけではなく、かなり高い支持率を示しています。
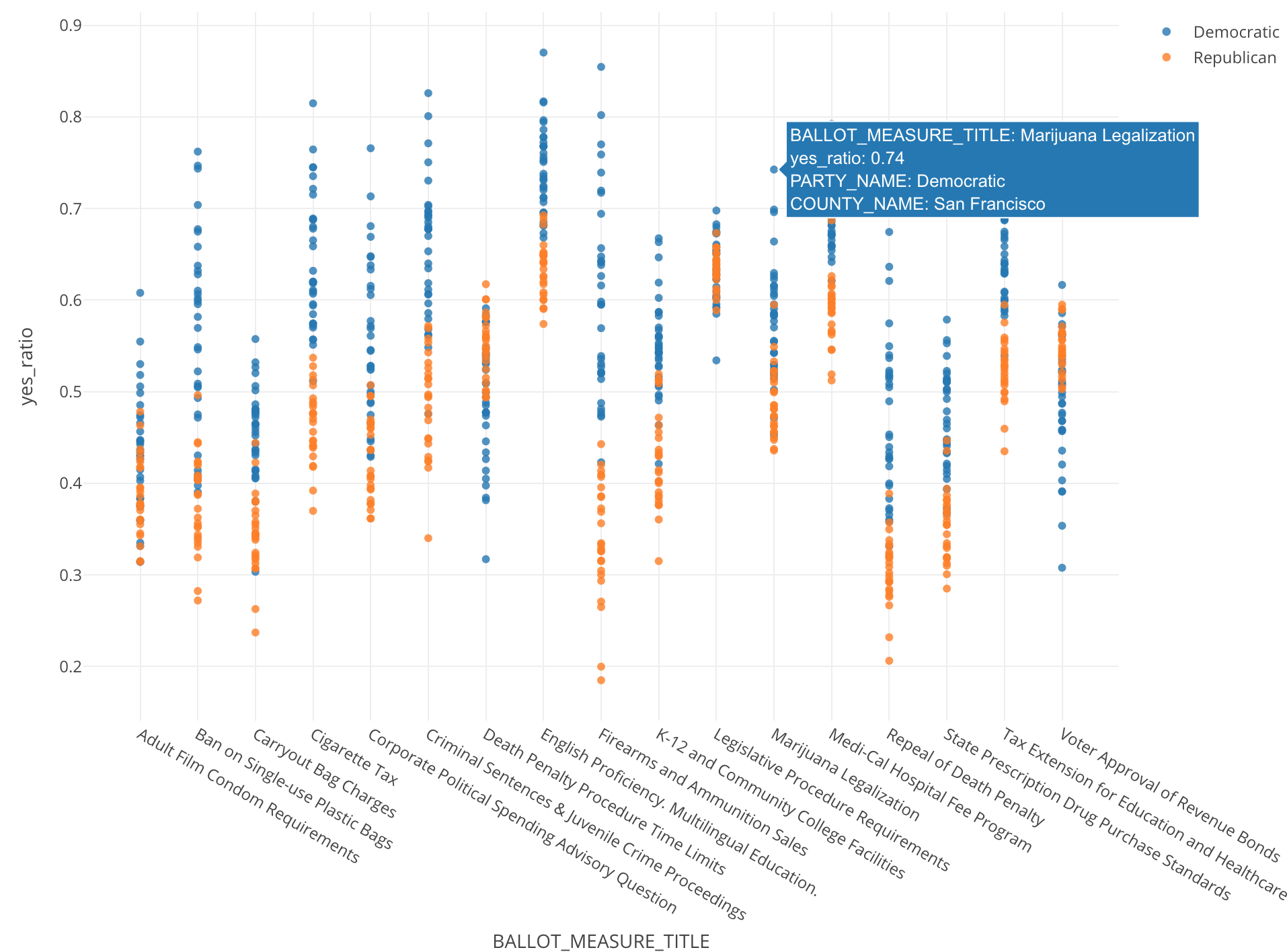
例えばマリワナの合法化に関して言えば、74%、ほぼ4人に3人が支持しているということです。
ちなみに、これは選挙結果がそうなっているということであって、私の個人的な見解とはまったく関係がありませんし、特に何らかの政治的な意図を持っているということではありませんので、よろしくお願いします。(笑)
ところで、このバイプロットのチャートからだけでもそれぞれのクラスターの特徴がだいぶわかってきましたが、他のチャートも見てみましょう。
箱ひげ図
こちらは、箱ひげ図ですが、それぞれの法案に対する支持率の分布をそれぞれのクラスターごとにグループ分けしたものです。
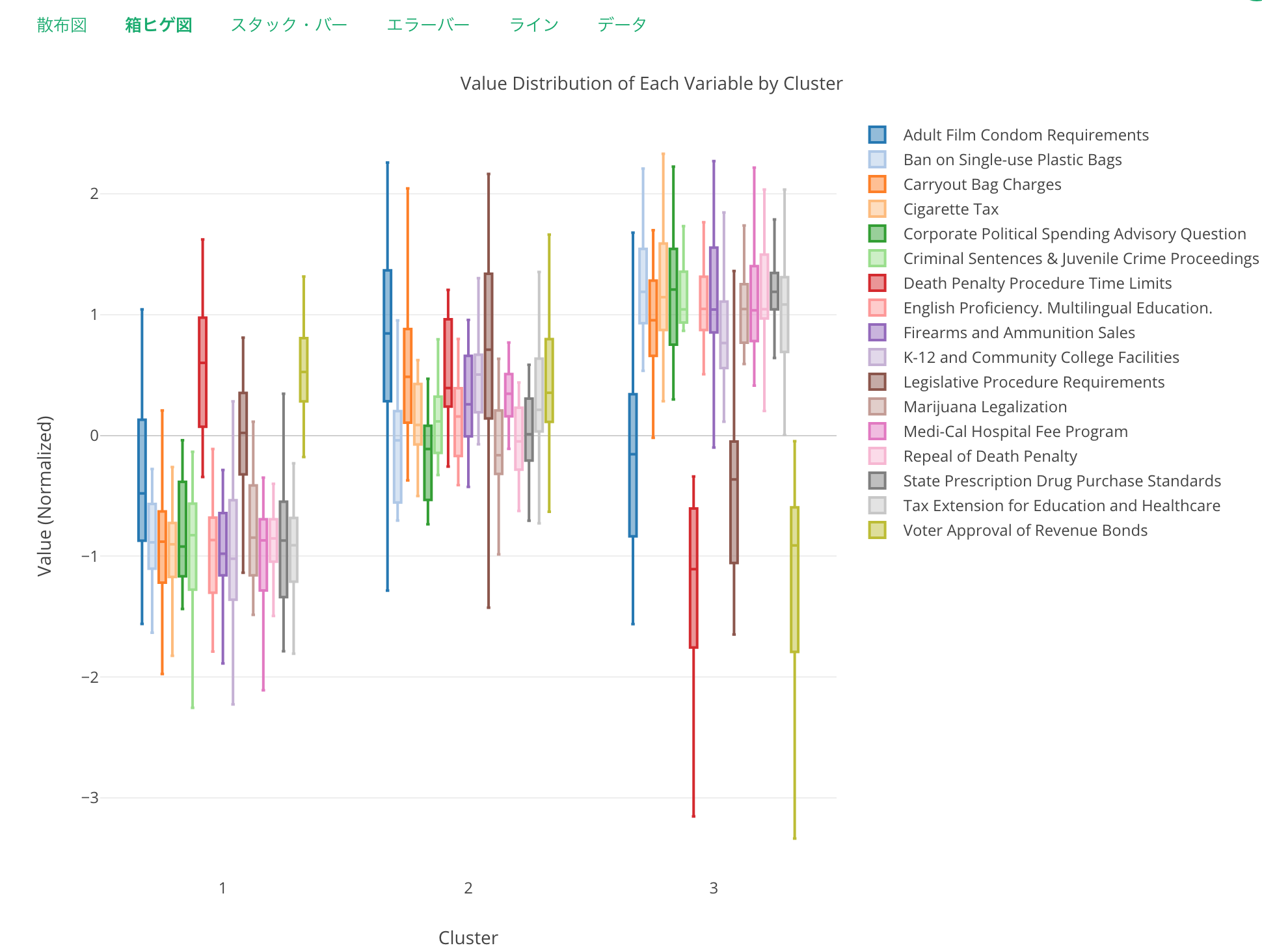
Y軸は支持率なのですが、その数字は標準化されています。標準化とは、簡単に言うと、平均からどれだけ離れているかを標準偏差で割って表したものです。これはつまるところ偏差値と同じようなものです。ここでの1は偏差値の60を表し、-1は偏差値40を意味します。0が平均なのですが、偏差値でいうと50です。
実はこのチャートからはたくさんのインサイトを得ることができるので、私の個人的なお気に入りでもあります。
まずは、赤色の箱ひげを見てみてください。これは「Death Penalty Procedure Time Limit」という法案で、死刑判決が出た囚人に対する再審議の期間を短縮することを含んだ法案です。これに対して、クラスター1の群による支持率はほとんどが平均よりも高いレベルで分布しているのがわかります。逆に、クラスター3はどの群も平均よりも低い支持率を示し、さらにその分布から反対する群はほかに比べてかなり大きく反対していることが見えます。
ちなみに、こちらが先ほども出てきた、もとの支持率のデータをチャートで表したものです。
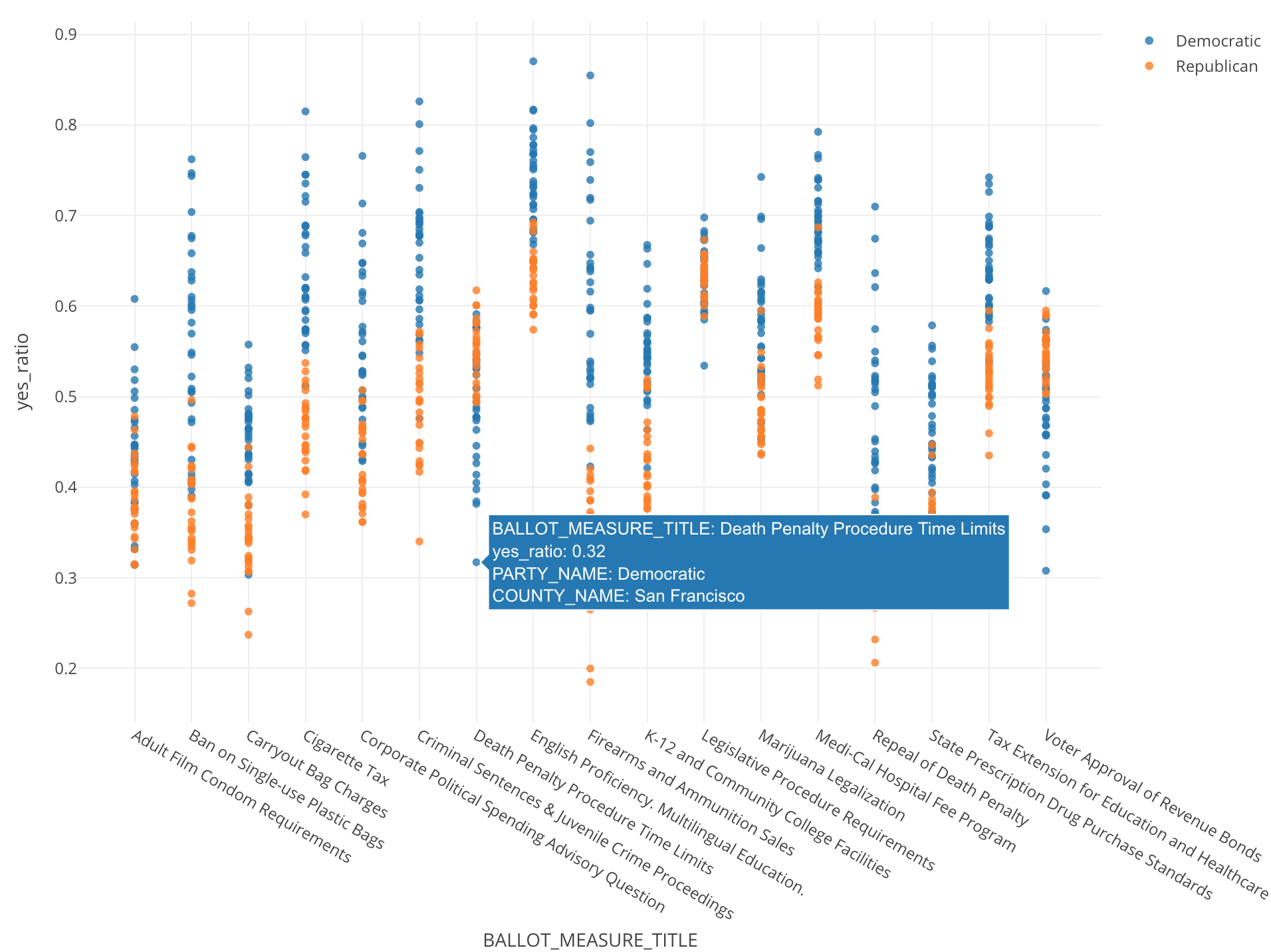
この「Death Penalty Procedure Time Limit」という法案に対して、サンフランシスコは他に比べて飛び抜けて大きく反対していることがわかります。
また、「Adult Film Condom Requirement」である青い箱ひげを見ると、クラスター2は高い位置で分布し、逆にクラスター1と3は比較的低いのがわかります。
ここから、この法案はクラスター2にとっては重要で支持すべきもののようですが、逆にクラスター1と3にとってはほかの法案に比べて特に賛成でも反対でもなく、ある意味どうでもいいということのようです。(笑)
ライン
ラインのタブの下にあるのは、データサイエンスの世界ではよく「パラレル・コーディネート」と呼ばれるチャートです。
一つ一つの線は1つの郡を表し、X軸になるそれぞれの変数(列)に対してどのような値を持っているのかを表しています。
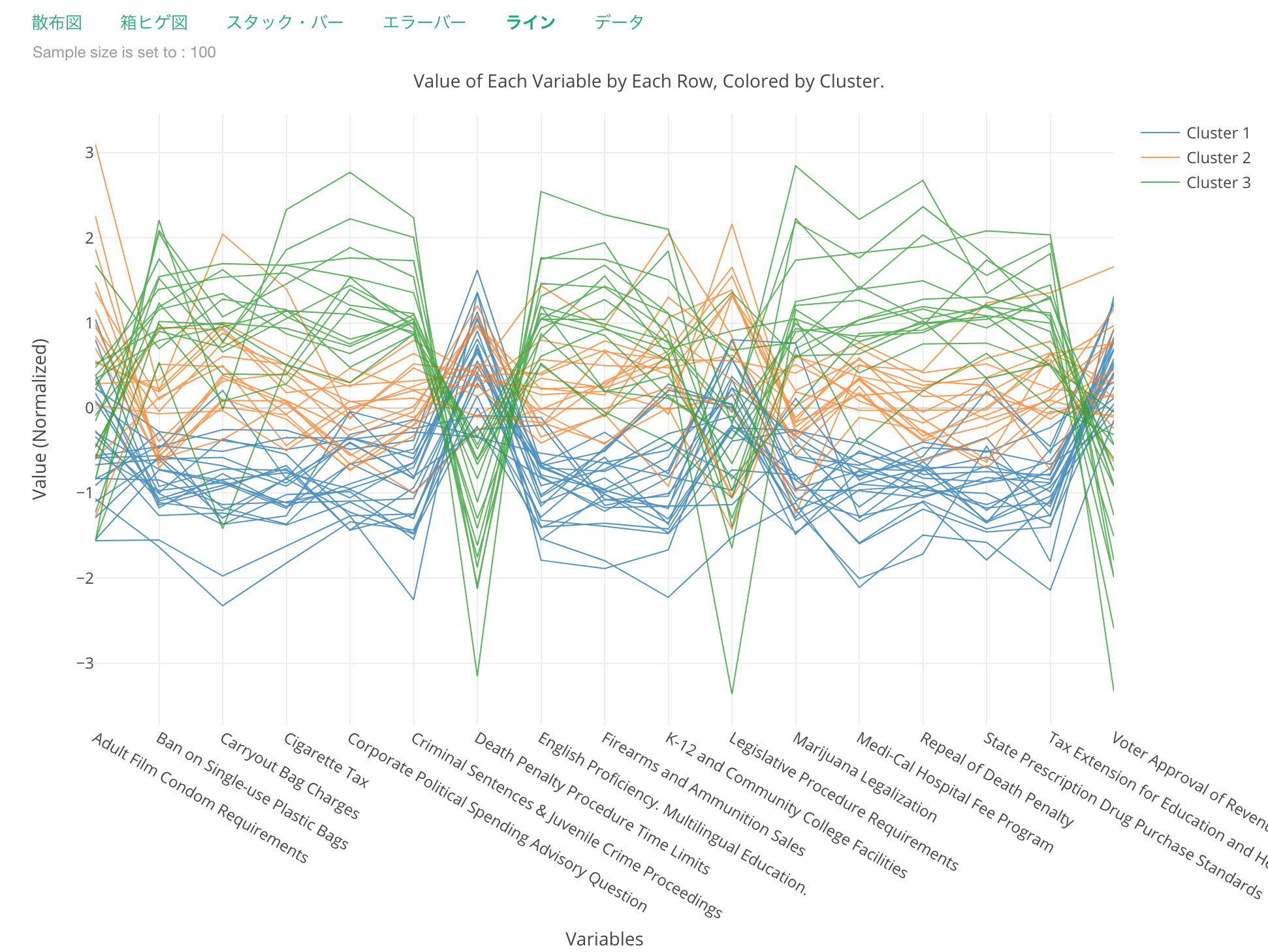
これを見ると、緑色のクラスター3はほとんどの法案に対する支持率が高いようですが、Death Penalty Procedure Limits, Voter Approval Revenue Bondsのようないくつかの法案では下に大きく触れているのがわかります。
さらに、この緑のクラスター3に属する郡は「Adult Film Condom Requirements」などいくつかの法案に対してはすべての群が賛成または反対ということではなく、結構揺れているというのがわかります。
エラーバー
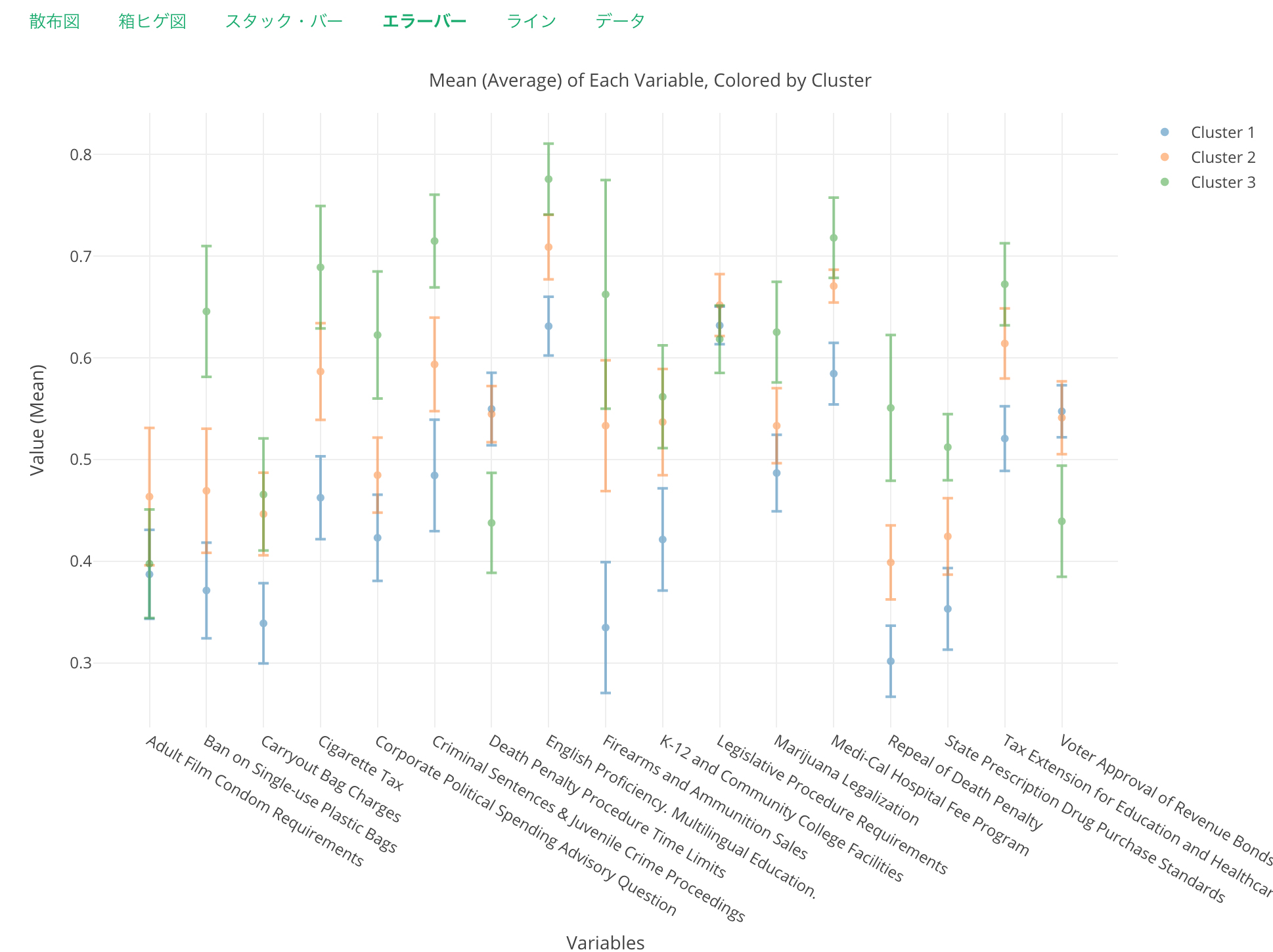
これは、エラーバーというタイプのチャートですが、慣れてない人には一見複雑そうに見えるかもしれませんが、実はこれは見た目よりももっと単純なものです。X軸はそれぞれの法案、Y軸は支持率を表し、それぞれの線(ここではバーと呼びます)の真ん中にある点はそれぞれのクラスターに属する郡たちの、それぞれの法案に対する支持率の平均です。
そして、バーの長さは、ここでは標準偏差-1から1までを表しています。これは偏差値に40から60までということです。ちなみに、平均は偏差値50です。
このバーの長さはプロパティから変えることができます。
このチャートがいいのは、どの変数(列)がクラスターをより分けているのかがわかりやすいという点です。
例えばタバコに対する税金を上げようとする「Cigarette Tax」という法案を見てみましょう。
これをみると標準偏差1の分布だとそれぞれのクラスターはくっきりと分かれているのがわかります。そして、青いクラスター1は0.5よりも低いので、このクラスターは基本的にこの法案に反対の群の集まりだろうということが推測できます。
また、公立の学校で英語以外の言語を使って教育することをよしとするための、「English Proficiency Multilingual Education」という法案を見てみましょう。
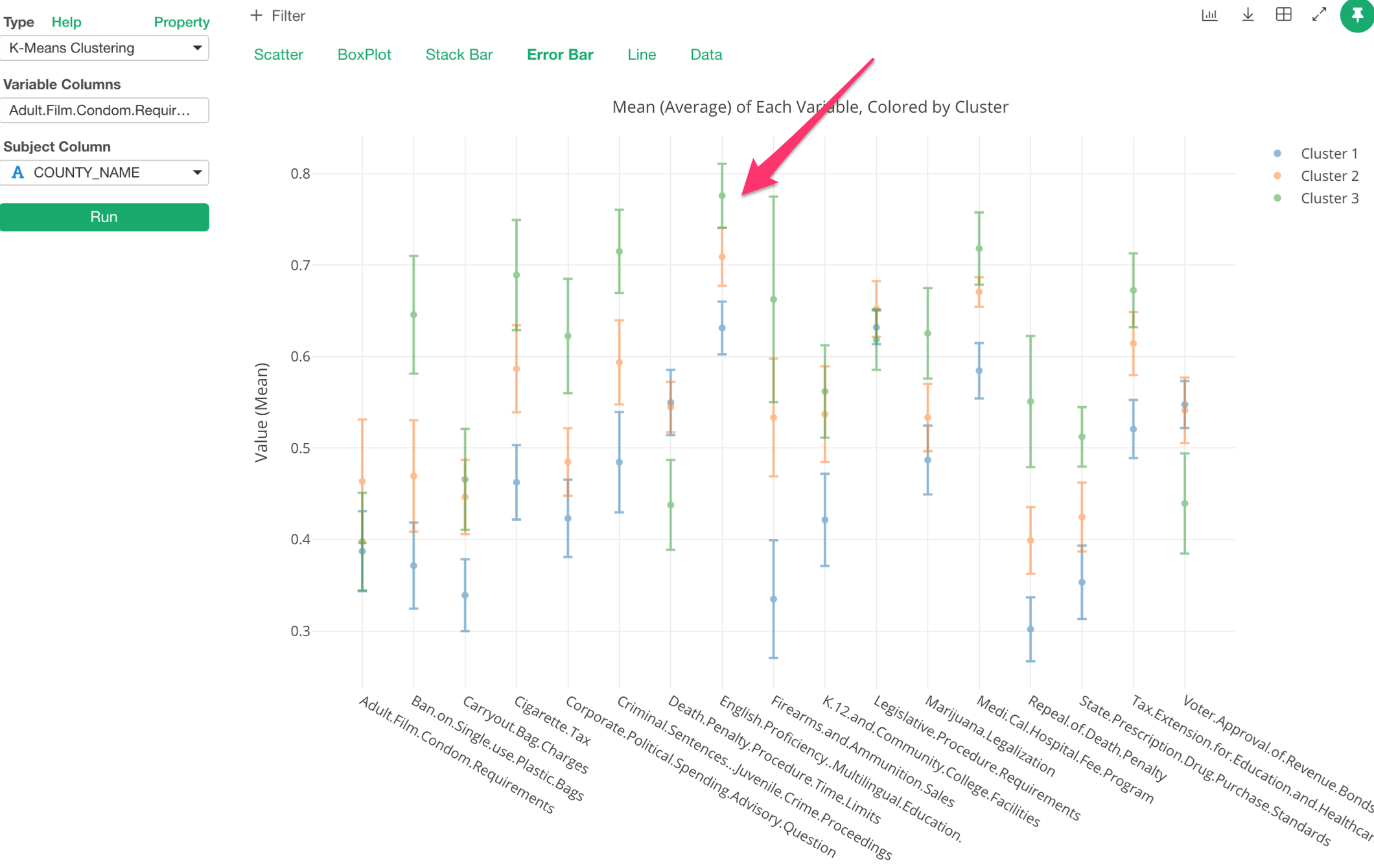
これもそれぞれのバーが交じることがないので、比較的それぞれのクラスターごとでの分布に違いがあるのがみてとれます。しかし、どれも0.5以上ですので、クラスターごとにどれだけ支持するかには違いがあるものの、どのクラスターにも支持されているのがこの法案ということがわかります。
最後に、「Legislative Procedure Requirements」という議会で議決するための法案は72時間前までにプリントかインターネットで公開を義務付ける、という法案を見てみましょう。
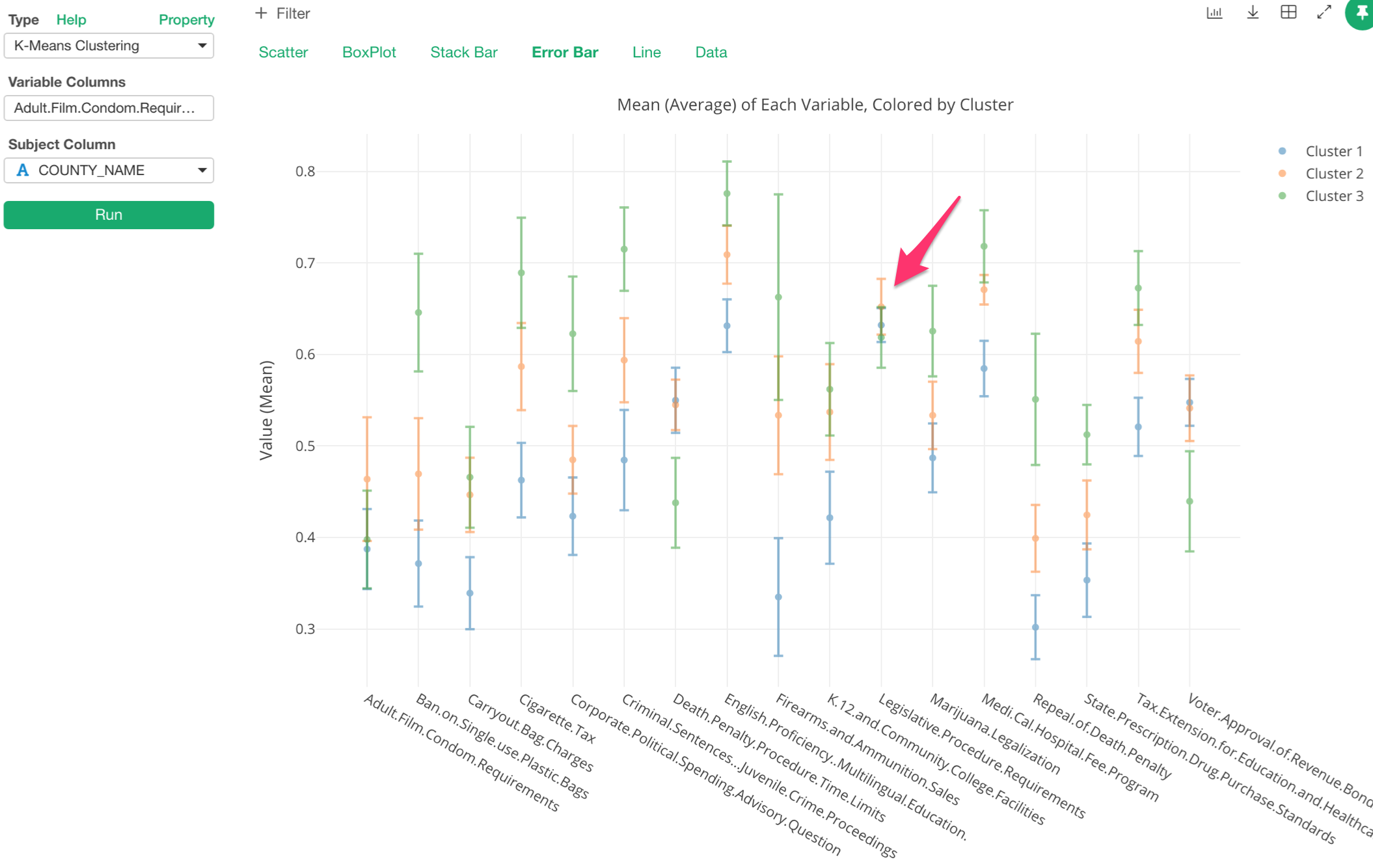
これをみると、どのクラスターもたいして差はなく、またどれも0.5より上にあるので、同じように支持しているのがわかります。つまり、この法案は、ここでのクラスターの特徴を説明するのには役立たないと言えます。
Stack Bar
最後に、スタック・バーのチャートを見てみましょう。
これは、「比較対象の列」にアサインした列の値がそれぞれのクラスターに占める割合を見ることができます。
現在「比較対象の列」は郡になっていますが、このデータはそもそも一行、一郡となっているので、バーの中を見てもその割合は特に変わるわけではないので、あまり意味がありません。
ところが、「比較対象の列」に他の属性の列をアサインすることで、実はものすごく面白くなったりします。
例えば、このデータの場合は大統領選挙での投票結果をもとに、それぞれの郡が民主党と共和党のどちらによっているのかを表した、PARTY_NAMEという列があります。これを「比較対象の列」にアサインして、もう一度実行すると、以下のようなチャートが得られます。
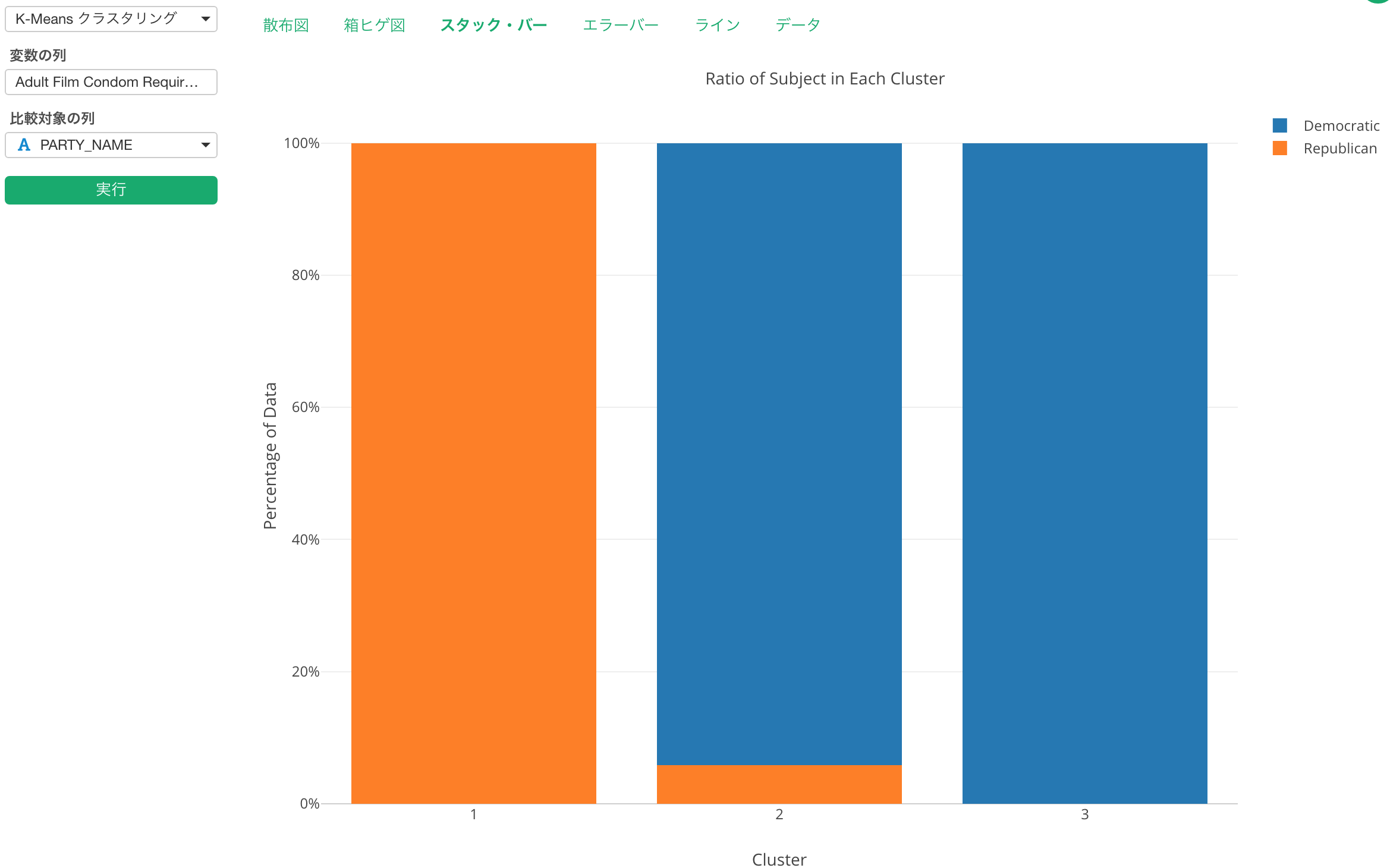
これを見ると、クラスター1というのは共和党よりの郡で、クラスター2と3は民主党よりの郡の集まりだということがわかります。
こうして、アナリティクス・ビューでK-Meansクラスタリングを使うことで、自動的に生成されるチャートを使って可視化しながら、それぞれのクラスターごとの特徴や、興味のある対象の(この場合はカリフォルニア州の郡でした)類似性を効率的に理解していくことができました。
このポストでは、クラスターの数はデフォルトである3として見てきましたが、それでは、そのクラスターの数はどのように設定すればいいのかということに関して興味のある方は以下のポストを見てみてください。
K-Meansクラスタリングがアナリティクス・ビューに加わったことで、以前よりもいっそうこのアルゴリズムを使ってデータを分析していくのが簡単になったと思います。私も、最近は初めて手にするようなデータは特に、探索的データ分析の最初の段階で、まずはクラスタリングをかけて全体像を把握するというかたちで使いまくっています。(笑)
みなさんもぜひ試してみてください!
何か質問などありましたら、support@exploratory.io まで、お気軽にご連絡ください。