3つ以上の平均値の比較
女子学生:2つのグループ間の平均の違いについて調べるときはt検定が使えますが、グループの数が3つ以上の場合はどうするんですか?
男子学生:その場合はANOVA検定を使えばいいんですよね。
女子学生:ANOVAってどういう意味なんですか。
先生:ANOVAはAnalysis Of Varianceの略で、日本語ではANOVA検定、または分散分析と呼ばれます。
女子学生:分散に関する分析ということですか。
先生:平均値の違いに関する分析なんだけど、分散、つまりデータのばらつきを元に分析するからそういう名前がついています。この章では、ANOVA検定と呼ばれる検定手法について見ていきたいと思います。
ANOVAの基礎
前章では、2つのサンプル平均を比較するt検定を学びましたが、グループが3つ以上ある場合には使えません。こうした場合に使われるのが「ANOVA検定」です。ANOVA(Analysis of Variance)は「分散分析」とも呼ばれ、データのばらつきを基に、複数のサンプル平均に有意な差があるかどうかを判断する手法です。
ANOVA検定にはいくつかの種類があります。最も一般的なのは One-way ANOVA(一元配置分散分析) です。これは1つの説明変数に含まれる複数のグループの平均値の違いが統計的に有意かどうかを分析するときに使います。例えば、3つの学校の数学の平均点の違いを調べる場合などです。
一方、2つの説明変数の影響を同時に調べたい場合は Two-way ANOVA(二元配置分散分析)を使います。例えば、3つの学校の平均点の違いに加えて男女比の違いも考慮したい場合です。Two-way ANOVAを使えば、学校の違いによる影響と性別の違いによる影響を同時に評価できます。
さらにANOVA検定には他にもいくつかのタイプがあるのですが、本書ではその中でも一般的によく使われるOne-way ANOVA(一元配置分散分析)を取り上げます。この章ではこのタイプの検定を単純にANOVA検定と呼びます。
学校のテスト結果の分析
これから学校の数学の成績を例にしてANOVA検定を解説していきます。
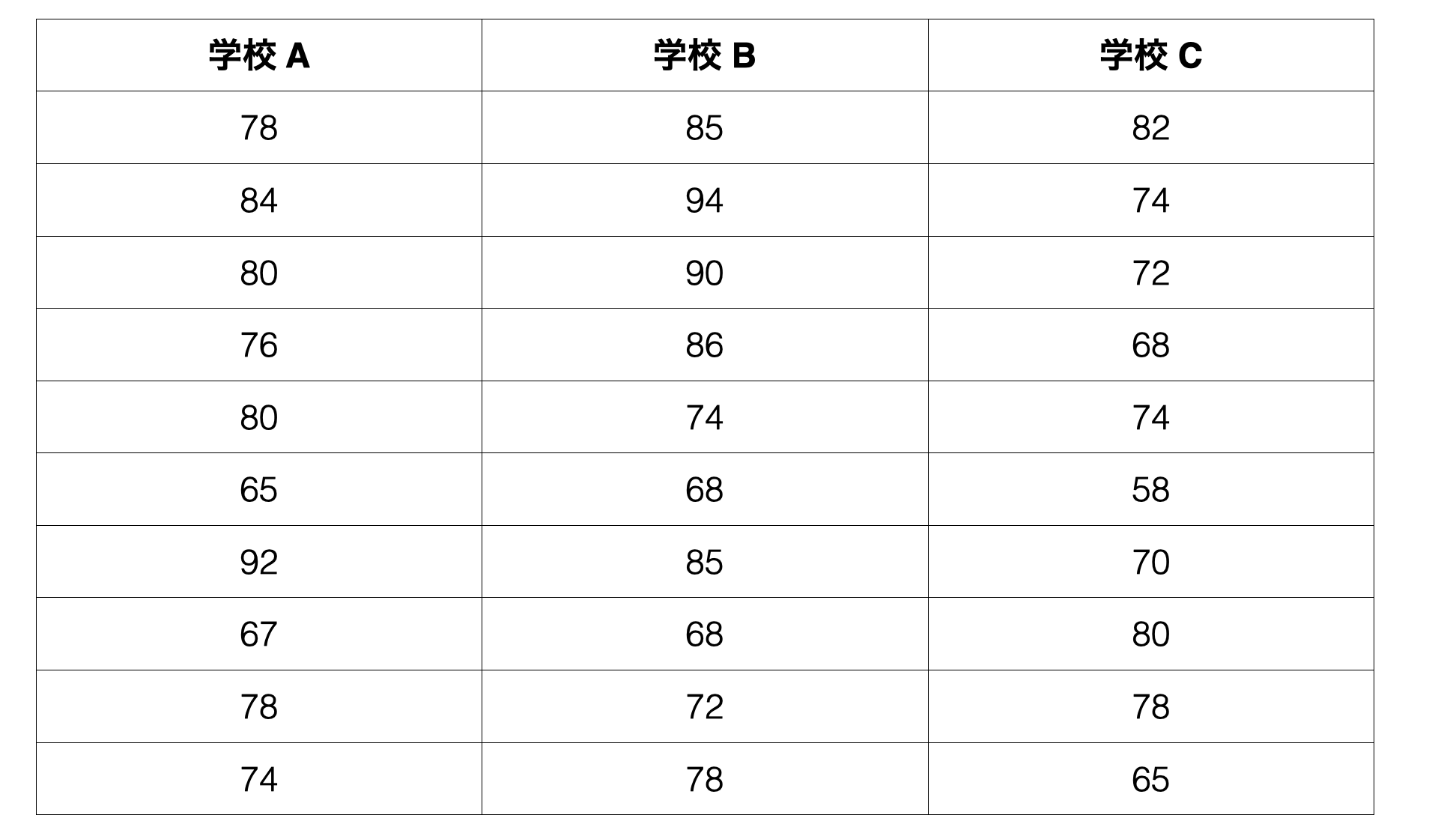
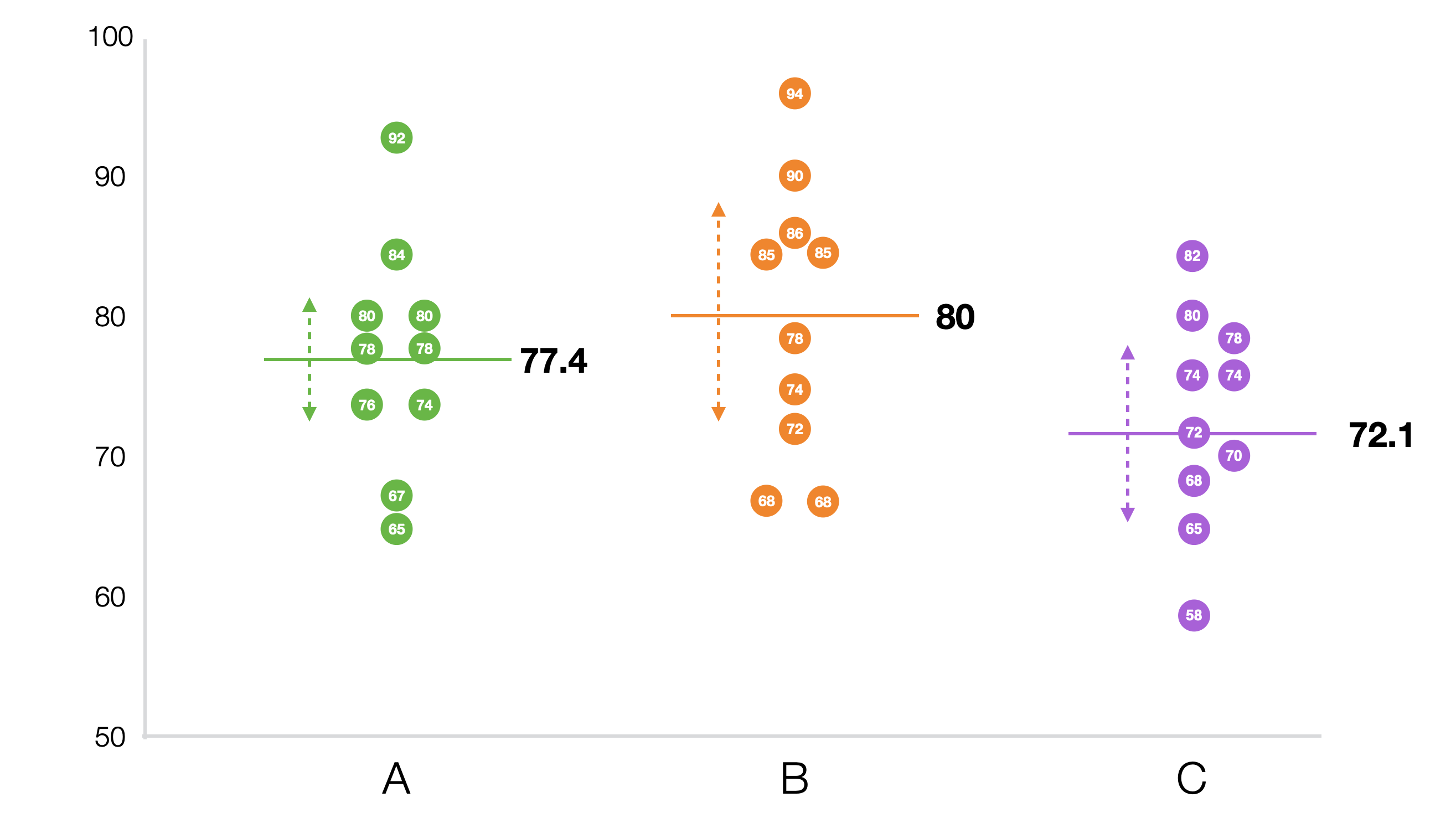
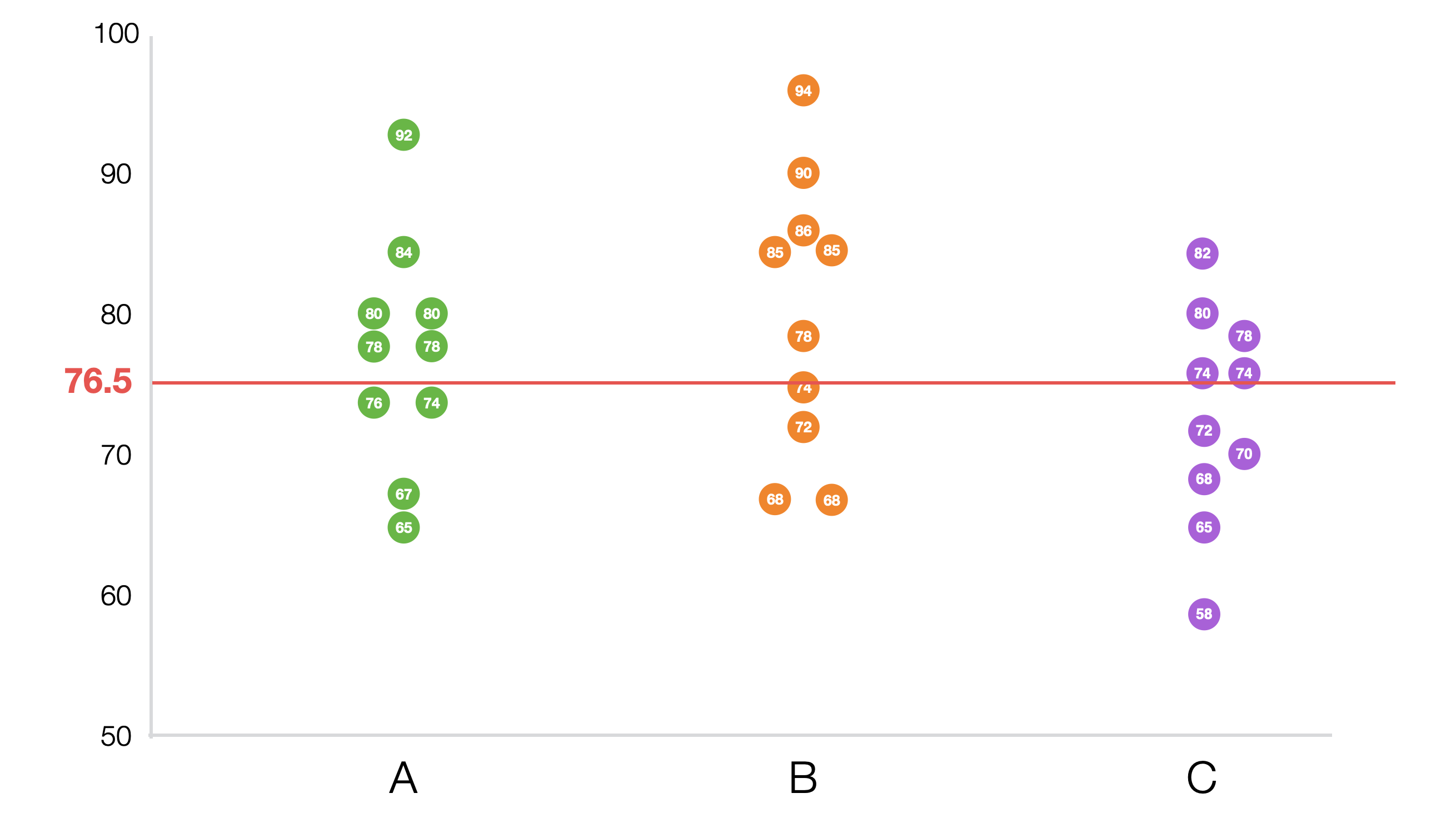
ある学区には3つの学校があります。各学校の生徒の数学の成績は次の通りです。
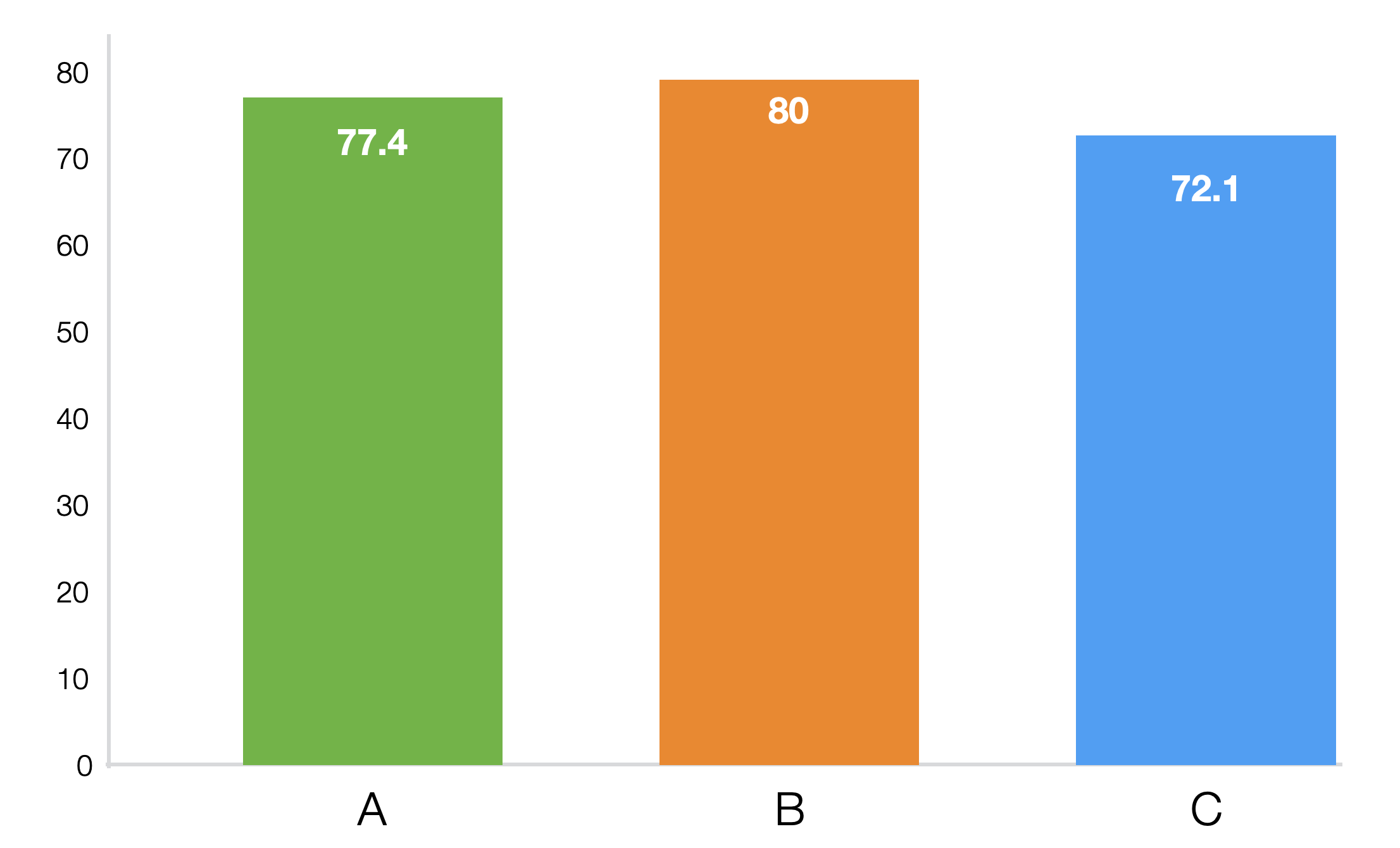
各学校の平均点をチャートにしたものが以下です。
平均点を見ると学校Bが最も高く、その次にA、Cの順です。しかし、この差が統計的に意味のある差なのか、それとも単なる偶然やデータのばらつきによるものなのかは、この平均だけでは判断できません。 グループが2つならt検定で評価できますが、今回は3つのグループがあるためANOVA検定を使います。
帰無仮説
ANOVA検定における帰無仮説は、「複数のグループ間に平均値の差はない」 というものです。学校の例では、3つの学校の平均点はすべて等しいと仮定します。
帰無仮説が棄却される場合の意味は、単純に「差がある」ということではなく、「複数のグループのうち少なくとも1つの平均値が他のグループと有意に異なる」 ということです。つまり、学校の例では、少なくとも1校の平均点が他校と異なることを示しています。
ばらつきの分析
データは常にばらつきを持っています。そこで、複数のグループ間の平均値の差が、偶然によるばらつきの範囲内か、それとも統計的に有意に大きいか を判断する必要があります。
t検定では、2つのグループ間の平均値の差を標準化したt値を用いて差の有意性を判断しました。ANOVAではグループが3つ以上あるため、単純な差ではなくグループ間の平均のばらつきを指標として使います。ANOVAはこの考え方から「分散分析」と呼ばれます。
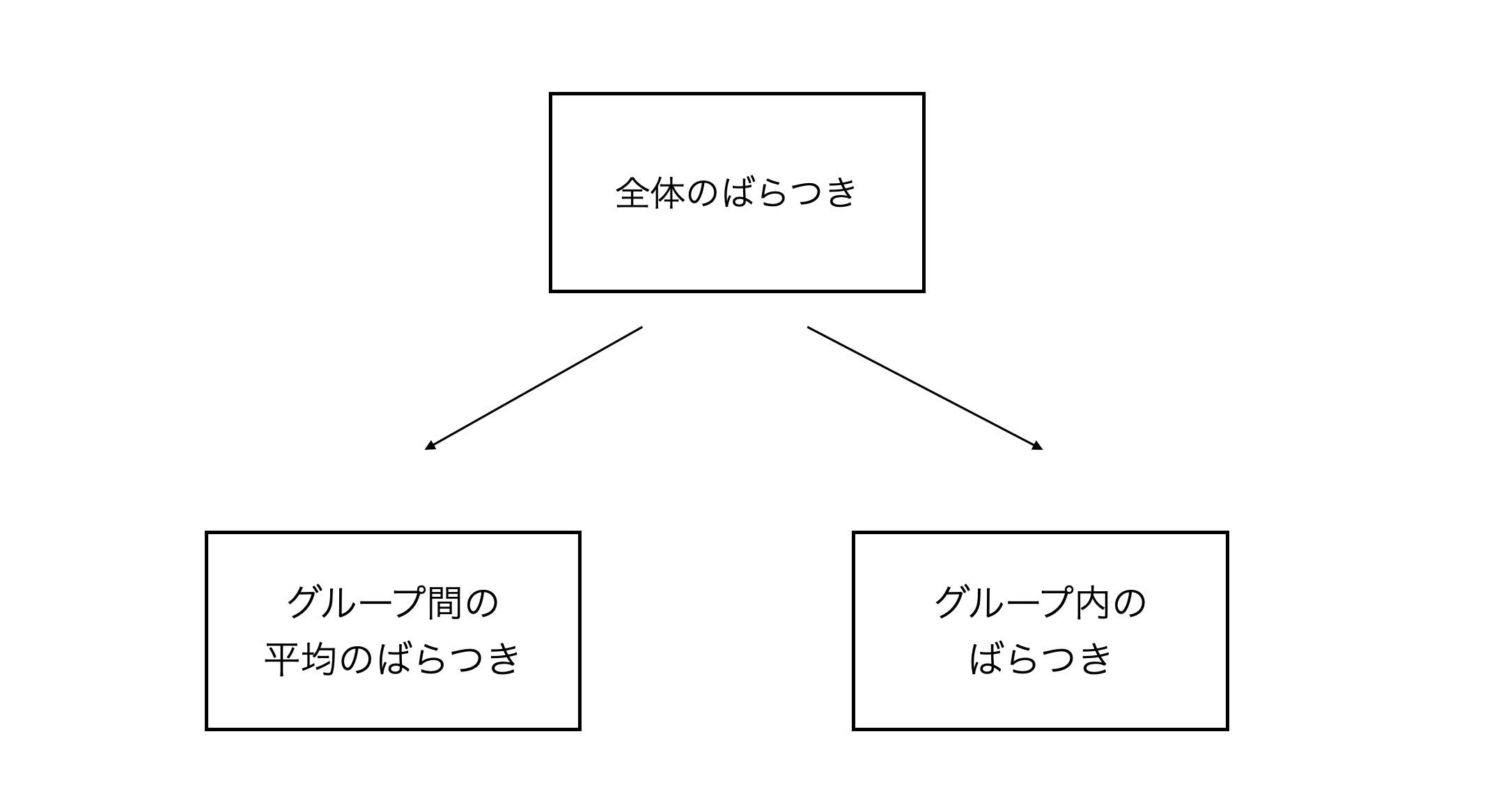
データ全体のばらつきは次の2種類に分けることができます。
- グループ間のばらつき:学校ごとの平均点の違いによるばらつき
- グループ内のばらつき:各学校の生徒の個人差によるばらつき
学校間の平均のばらつきが大きければ、学校の違いが成績の差に影響している可能性があります。逆に小さければ、学校間の違いはほとんど影響していないと考えられます。
グループ間のばらつきが統計的に有意かどうかを評価するには、グループ内のばらつきと比較します。グループ内のばらつきは、学校の違いでは説明できない他の要因(例えば、個人差、環境、偶然など)によるばらつきです。
各学校内のばらつき:
そして、学校間のばらつきがグループ内のばらつきに比べてどれだけ大きいか を表すのが F値で、以下のように計算されます。このF値をもとに、学校間の平均点の差が統計的に有意かどうかを判断します。
\[\begin{aligned} F値 = \frac{グループ間の平均値のばらつき}{グループ内のばらつき} \end{aligned}\]F値の計算ステップ
ANOVA検定でF値を求めるには、グループ間の平均値のばらつきとグループ内のばらつきを算出する必要があります。それぞれ順を追って詳しく見ていきましょう。
グループ間の平均のばらつき
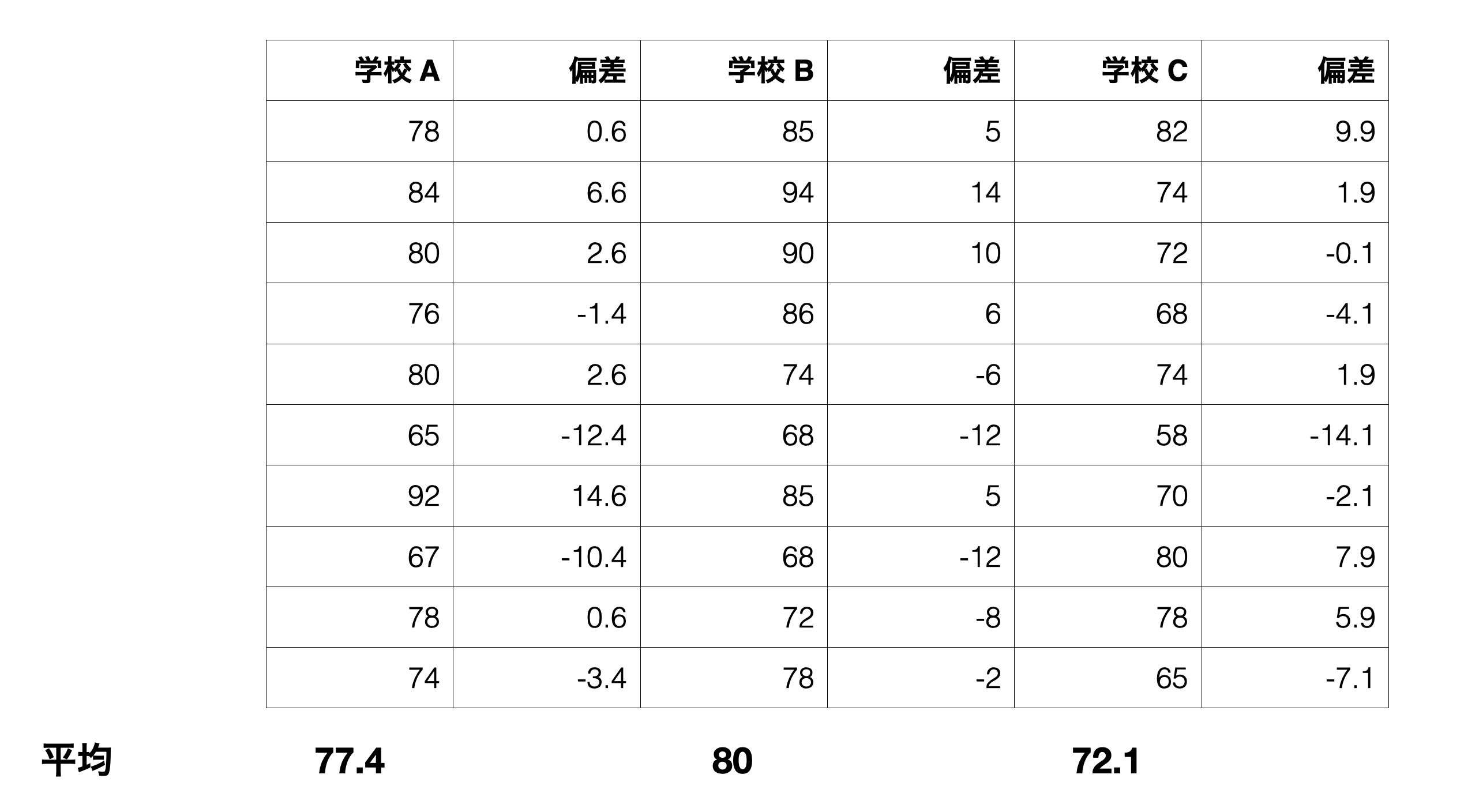
グループ間の平均値のばらつきとは、各グループの平均値が全体の平均値からどれだけ離れているかの大きさを示すものです。統計的には、「グループ間2乗和」と呼ばれますが、これを実際に計算してみましょう。
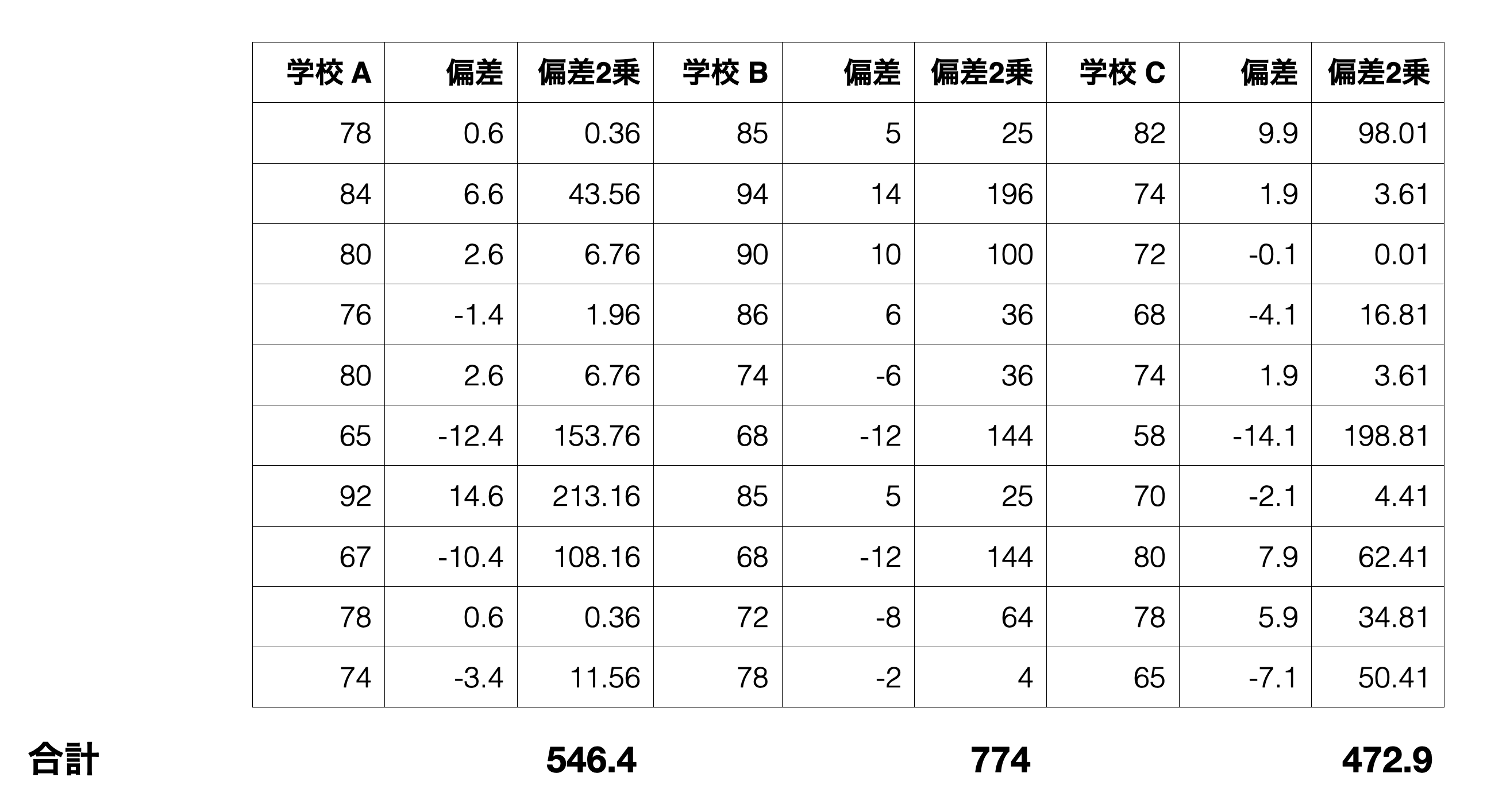
まず、全体の平均値である76.5と各学校の平均値との差を求めます。この差を偏差と呼びます。第4章の分散の計算の時にも見たように、偏差だけでは足し上げるとゼロになるので、偏差の2乗を計算します。
| 学校 | 平均スコア | 偏差 | 偏差の2乗 |
|---|---|---|---|
| A | 77.4 | 0.9 | 0.81 |
| B | 80 | 3.5 | 12.25 |
| C | 72.1 | -4.4 | 19.36 |
さらに、各グループの生徒数を掛けることで、各グループの重みを考慮します。これを行うことで、人数の違いによる影響を補正できます。
| 学校 | 平均スコア | 偏差 | 偏差の2乗 | 偏差の2乗 x 人数 |
|---|---|---|---|---|
| A | 77.4 | 0.9 | 0.81 | 8.1 |
| B | 80 | 3.5 | 12.25 | 122.5 |
| C | 72.1 | -4.4 | 19.36 | 193.6 |
これらの値を足し上げたものが「グループ間2乗和」、つまりグループ間の平均値のばらつきの2乗和です。
\[\begin{aligned} グループ間2乗和 = 8.1 + 122.5 + 193.6 = 324.2 \end{aligned}\]ここまでやってきたことを数式にすると以下のようになります。
\[\begin{aligned} グループ間2乗和 = Aの数 \times (Aの平均 - 全体の平均)^2 + Bの数 \times (Bの平均 - 全体の平均)^2 + Cの数 \times (Cの平均 - 全体の平均)^2 \end{aligned}\]グループ内のばらつきの大きさ
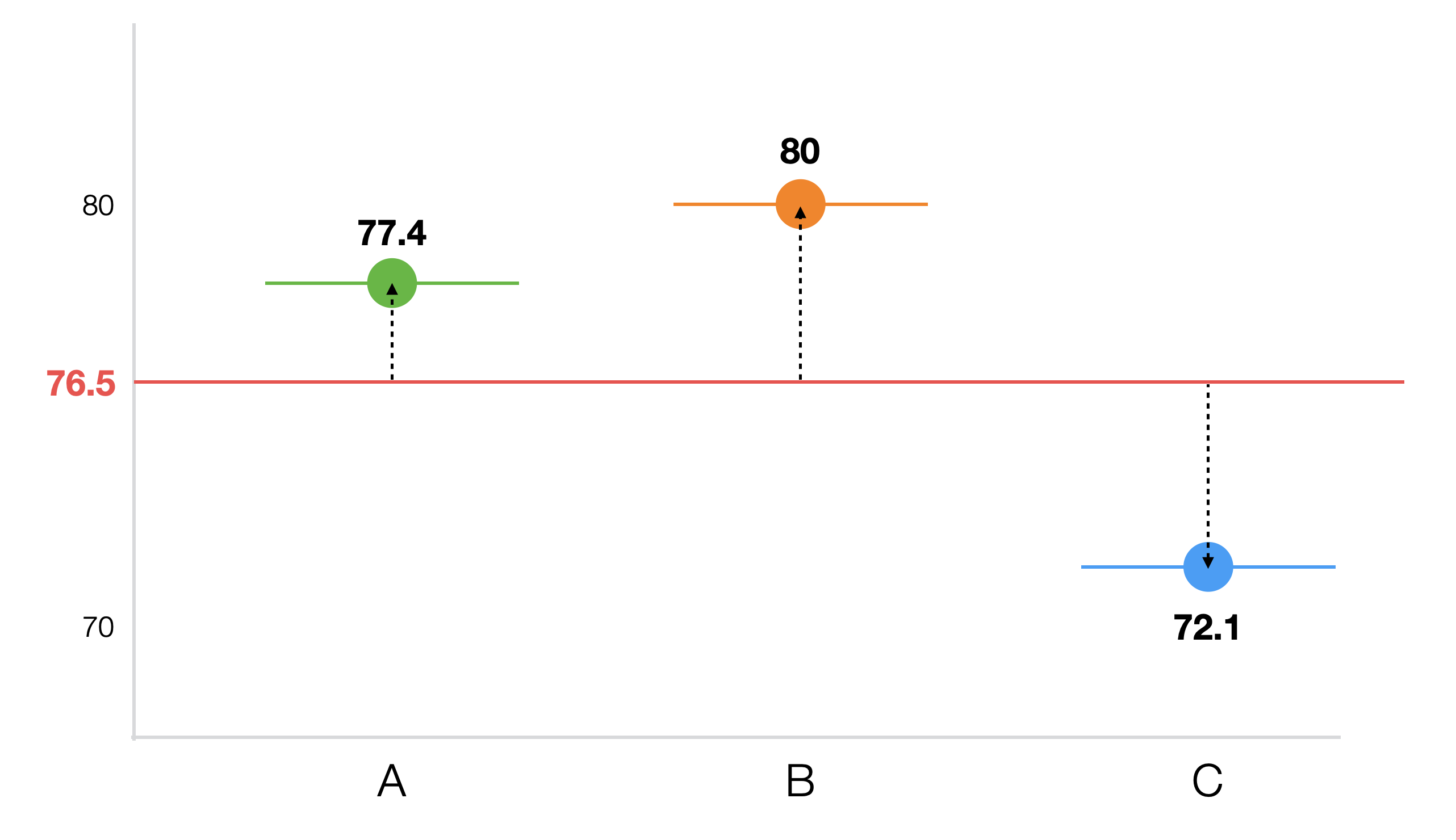
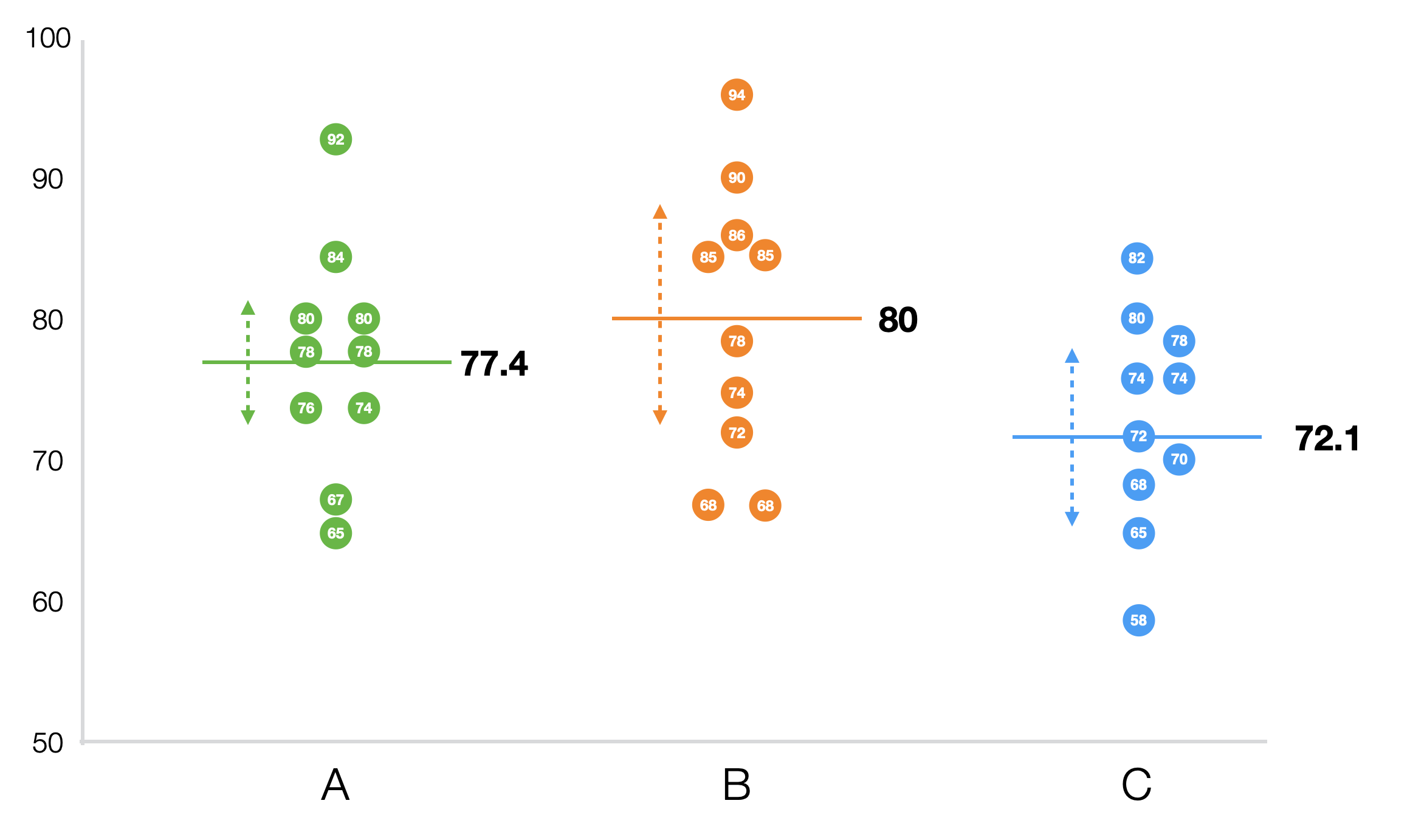
以下のチャートで見えるように、各学校の生徒のスコアはばらついていますが、この各グループ内のばらつきの大きさをこれから計算したいと思います。このばらつきのことを「グループ内2乗和」と呼びます。
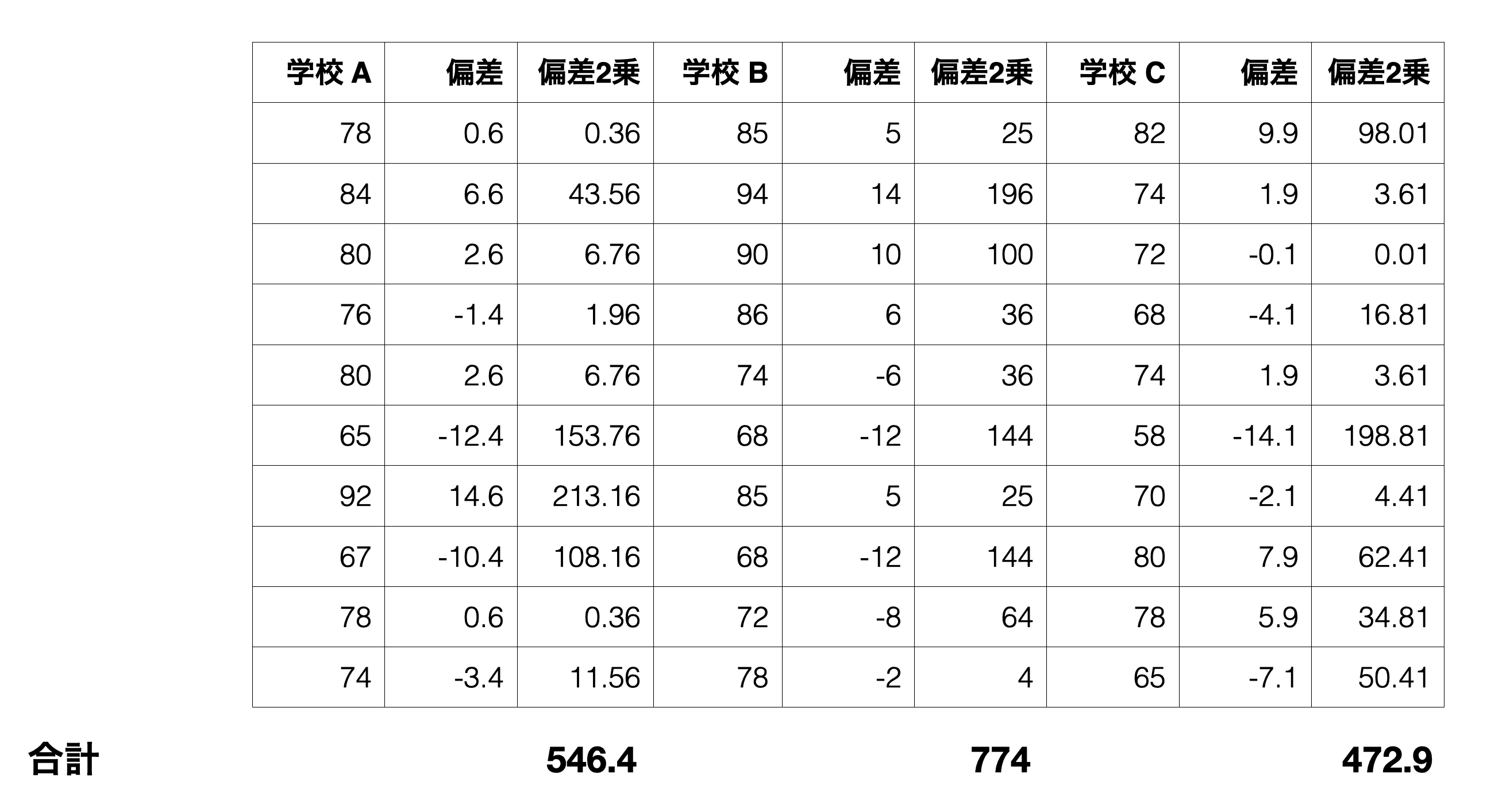
まず、各生徒のスコアとその生徒が属する学校の平均との差(偏差)を計算します。
そして偏差の2乗を計算し、各学校ごとに足し上げます。
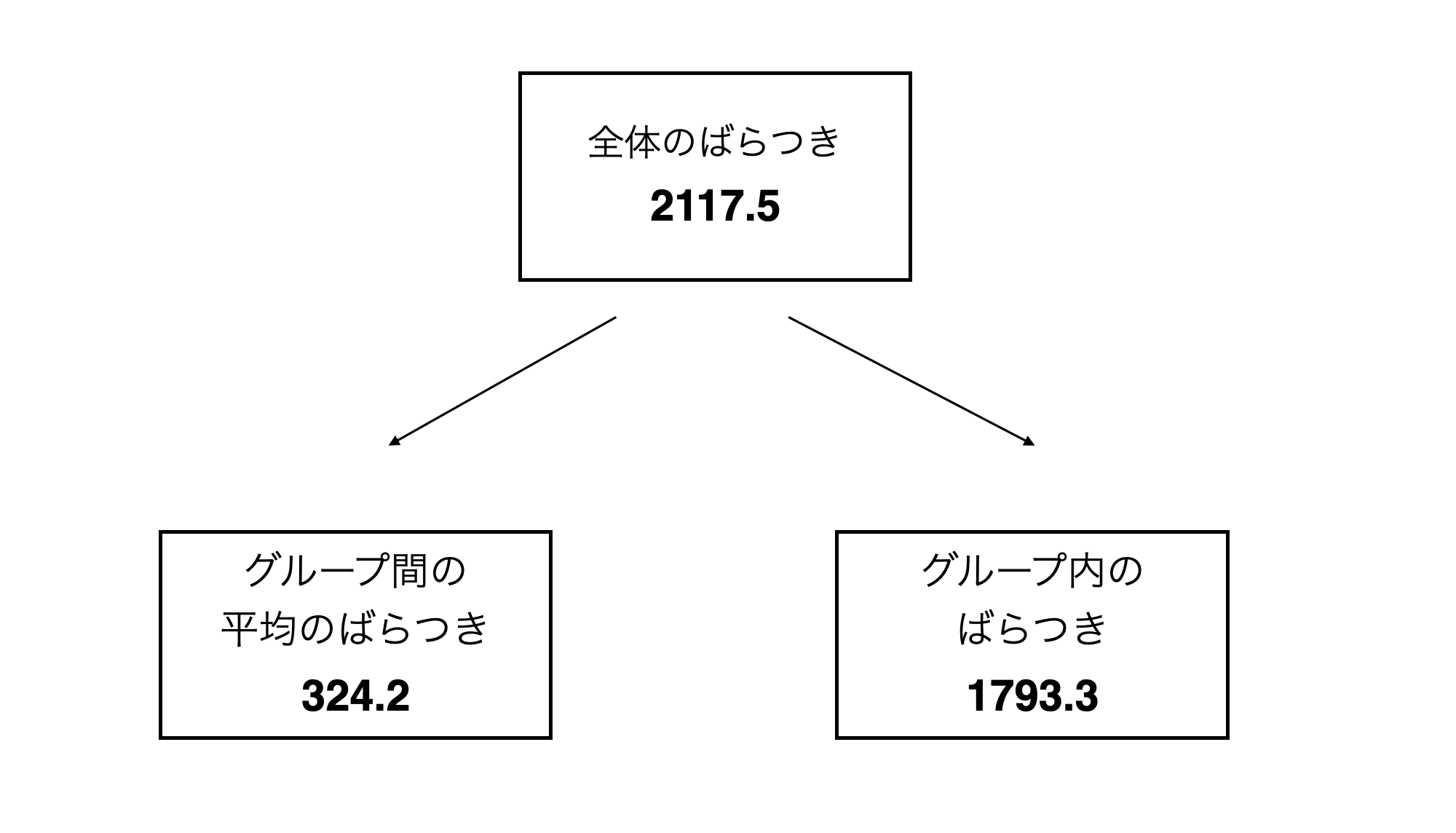
最後にこれらを全て足し上げると1793.3となりますが、これが「グループ内2乗和」です。
全体のばらつきの大きさ
最後に、全体のばらつきの大きさを計算しましょう。全体のばらつきとはそれぞれの値が全体の平均からどれだけばらついているかのことです。これを「全体2乗(または平方)和」と呼びます。これは、全ての生徒のスコアと全体平均との偏差の2乗を合計したものです。
これは「分散」と似ていますが、分散は「ばらつきの平均」であるのにたいし、全体2乗和は「ばらつきの和」です。
全体の平均値である76.5との差である偏差を計算し、2乗(偏差の2乗)します。
最後に、これら全ての偏差2乗の値を足し上げると2117.5となりますが、これが「全体2乗和」です。
ここで注目したいのは、これまでに計算した「グループ間2乗和」と「グループ内2乗和」を足し上げると先ほど求めた「全体2乗和」になるという点です。
\[\begin{aligned} 全体2乗和 = グループ間2乗和」+ グループ内2乗和 = 324.2 + 1793.3 = 2117.5 \end{aligned}\]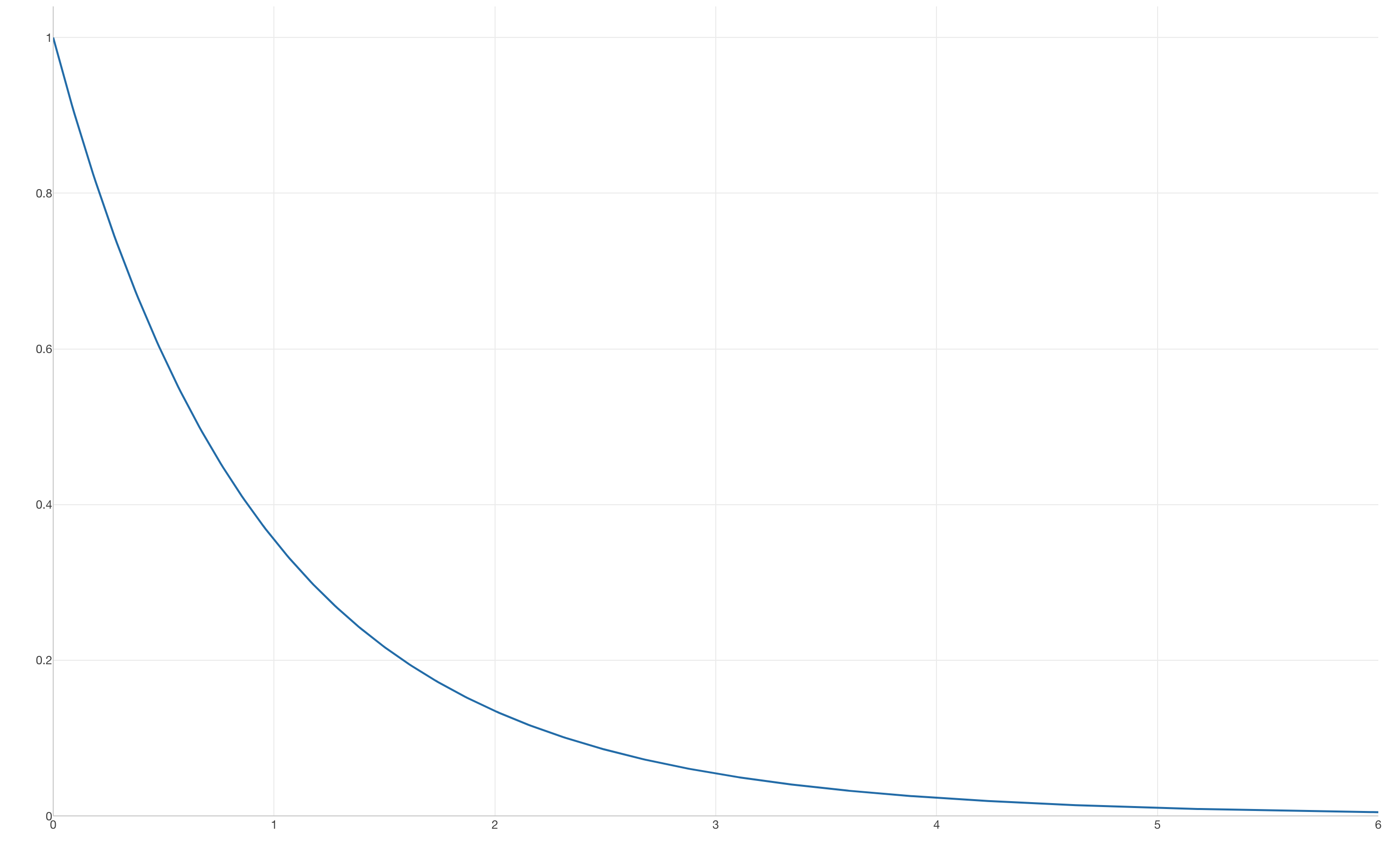
F値の計算
ここから、グループ間のばらつきとグループ内のばらつきの比率である F値 を計算していきます。
ところで一つ注意したいのは、F値の計算にはこれまで求めた 2乗和(平方和) をそのまま使うのではなく、「平均」を取ったものを使います。
グループ間のばらつきの平均
まず、グループ間の平均のばらつきの2乗和(グループ間2乗和)は 324.2 でした。 これをグループ数ではなく、自由度で割ることで グループ間2乗平均(Mean Square Between, MSB) を求めます。
注意:グループ間2乗和の平均を求めるために、学校の数3で割りたいところですが、「不偏分散」で見てきたように、サンプルから母集団のばらつきについて推定するためには、代わりに自由度で割る必要があります。
自由度は、全体の平均が決まっている場合に自由に動かせる値の数で計算します。
\[\begin{aligned} 自由度 = グループの数(N) - 1 = 3 - 1 = 2 \end{aligned}\]したがって、グループ間2乗平均は162.1と算出されます。
\[\begin{aligned} グループ間2乗平均 = \frac{(324.2}{2} = \frac{324.2}{2} = 162.1 \end{aligned}\]グループ間の平均値の差が大きいほど、この値は大きくなります。
グループ内のばらつきの平均
次に、グループ内のばらつきの和(グループ内2乗和)は 1793.3 です。 この値を元に グループ内2乗平均 を求めます。
ここでも、母集団に関する分散を推定したいわけですから、不偏分散を求めるために全員の数で割る代わりに自由度で割ります。
\[\begin{aligned} グループ内2乗平均 = \frac{グループ内ばらつきの2乗和}{自由度} \end{aligned}\]グループ内2乗平均を求める際の自由度は以下の式で求めることができます。
\[\begin{aligned} 自由度 = N(データ量) - グループの数 \end{aligned}\]今回の例では、全生徒数 30人 なので自由度は 27 です。
<Beyond Basic>
グループ内2乗和は各生徒のスコア各学校の平均値との差を元に計算しました。これは、各グループの平均値がわかれば自由に値を決めれるのはそのグループの最後の一人以外であることを意味します。そのため、自由度は以下のように計算できるのです。
\[\begin{aligned} 自由度 = (学校Aの生徒の数 - 1) + (学校Bの生徒の数 - 1) + (学校Cの生徒の数 - 1) = 全生徒の数 - 3 \end{aligned}\]<Beyond Basic>
すでに計算されたグループ内2乗和(1793.3)を、自由度(27)で割ると約66.42となりますが、これがグループ内2乗平均となります。
\[\begin{aligned} グループ内2乗平均 = \frac{グループ内ばらつきの2乗和}{自由度} = \frac{1793.3}{27} = 66.4185... \end{aligned}\]それでは、グループ間のばらつきとグループ内のばらつきが計算できたので、さっそくF値を求めてみましょう。
グループ間のばらつきとグループ内のばらつきの比率
最後に、グループ間2乗平均とグループ内2乗平均の比率であるF値を計算します。
\[\begin{aligned} F値 = \frac{グループ間2乗平均}{グループ内2乗平均} = \frac{162.1}{66.42} = 2.44... \end{aligned}\]このF値は、学校ごとの平均スコアの違いの大きさを示しています。値が大きいほど、グループ間の差が統計的に有意である可能性が高くなります。
F分布とP値による有意性の判断
F値を計算しただけでは、グループ間の平均値の差が有意かどうかは判断できません。 私たちが知りたいのは、F値が「偶然のばらつきの範囲内か、それとも統計的に意味のある差を示しているか」です。
そのために使うのが F分布 という確率分布です。
同じ母集団から繰り返しサンプルを抽出してF値を計算すると、そのF値のばらつきは F分布 に従うことが知られています。F分布の形は2つの自由度によって変わります。これらはF値を計算する際の分子と分母で使われた自由度のことです。
\[\begin{aligned} F値 = \frac{グループ間2乗平均}{グループ内2乗平均} \end{aligned}\]- 自由度 1 :グループ間2乗平均の計算に使われた自由度
- 自由度 2 :グループ内2乗平均の計算に使われた自由度
今回の例では、自由度は以下のようになります。
- 自由度1 = 2(グループの数 − 1)
- 自由度2 = 27(全データ数 − グループ数)
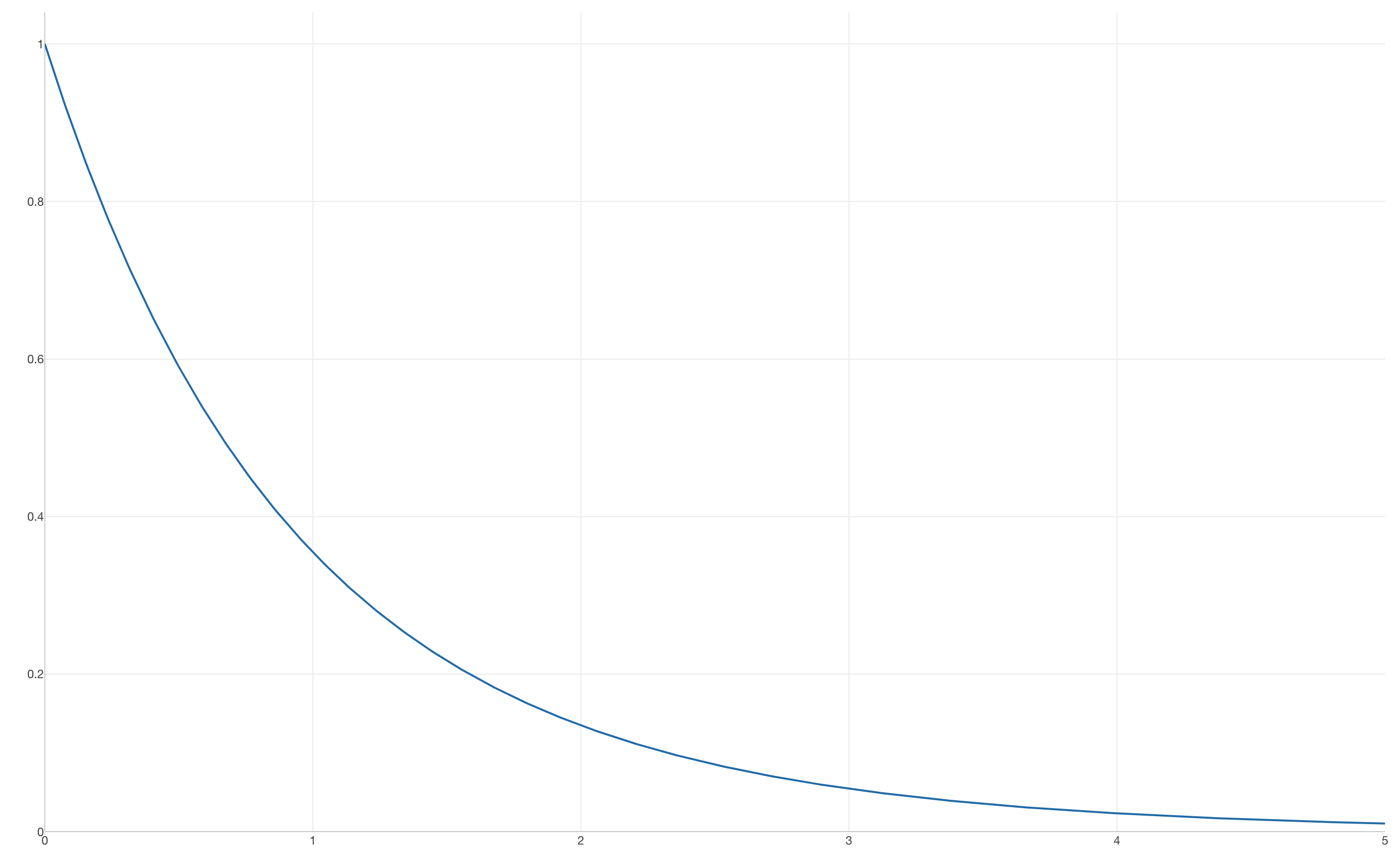
その場合のF分布は以下のような形となります。
F分布の特徴
- 値は0以上:F値は比率なので、0より小さくなることはありません。
- 片側検定:F値は0以上で、値が大きくなるほどグループ間の差が大きいことを示すため、常に片側検定で評価します。
- 形は自由度に依存:2つの自由度の値によって分布の形が変わります。
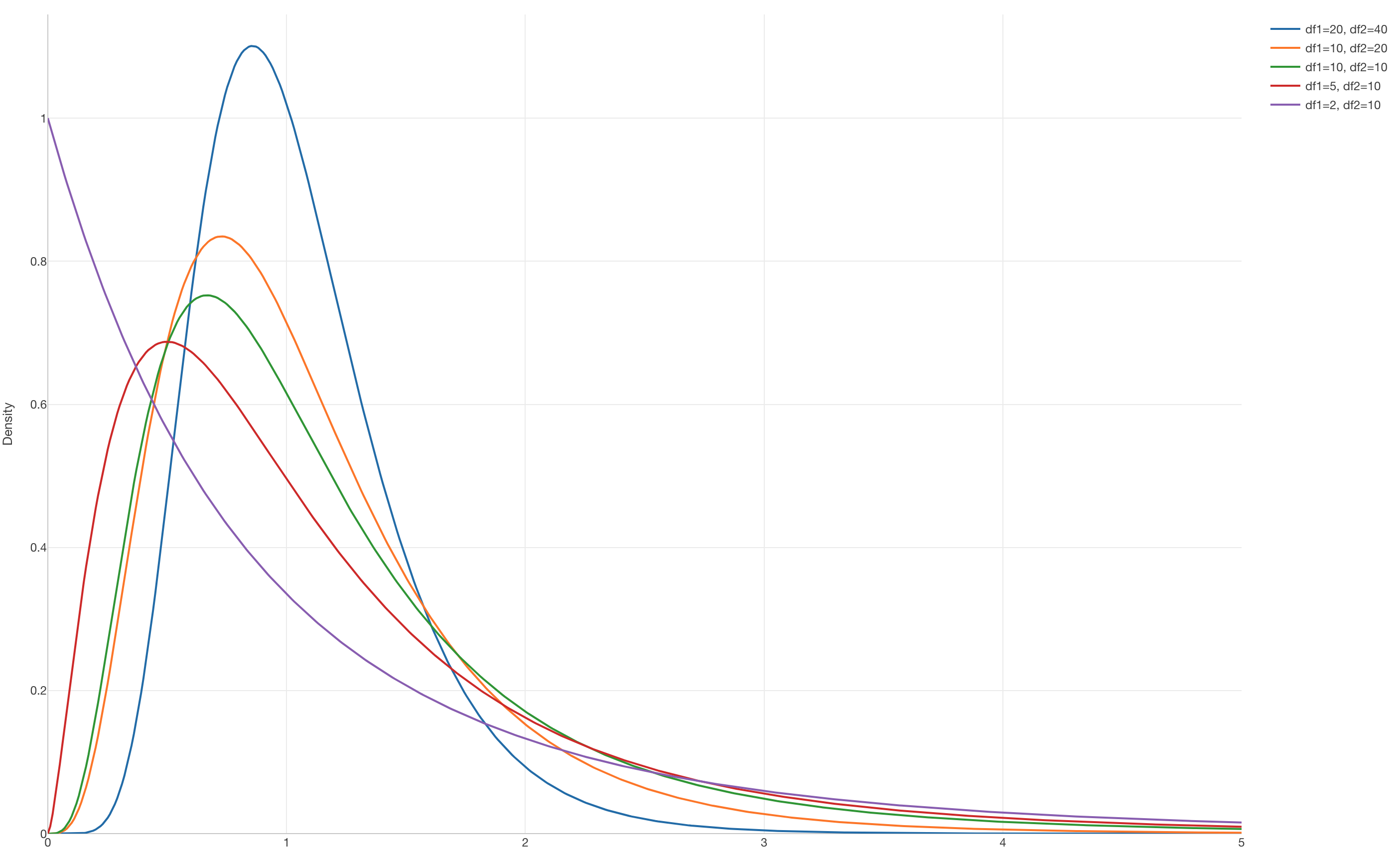
以下は2つの自由度の値を変えた時にF分布の形がどう変わるかをチャートにしたものです。チャート内のdf1、df2はDegree of Freedom(自由度)の略です。
P値を使った有意性の判断
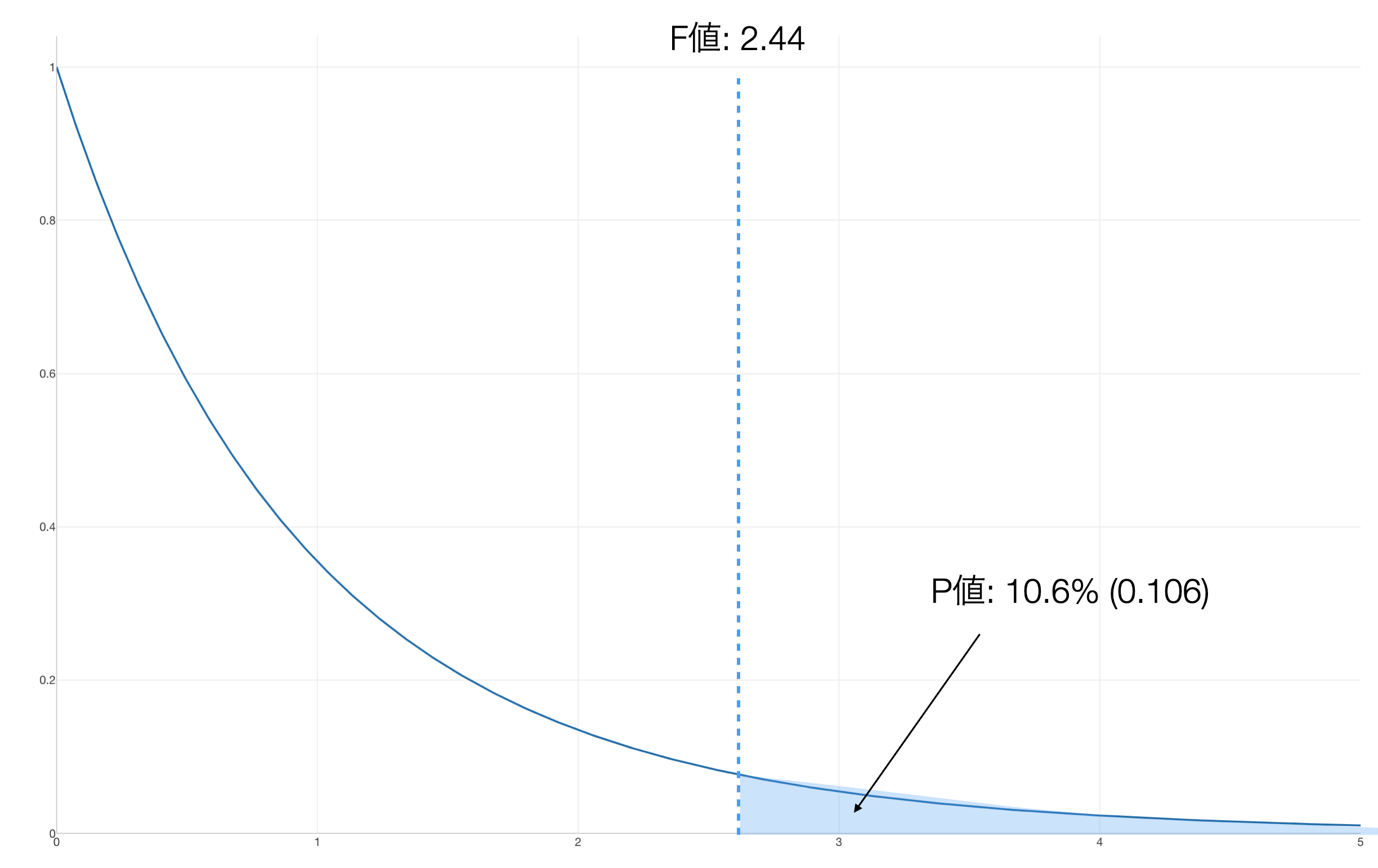
F分布を使うと、手元のデータから算出されたF値以上の値が得られる確率であるP値を求めることができます。
今回の学校の例では、F値が2.44であるため、F分布を使うとP値は約10.6%と算出されます。結論として、有意水準5%の下では、「3つの学校の平均の違いは統計的に有意である」とは言えません。

Let’s do it!
それでは、ここからは実際に Exploratory を使ってANOVA検定を行ってみましょう。 従業員データを使って、婚姻ステータスによる給料の違いが統計的に有意かどうかを調べましょう。
- プラスボタンをクリックして新しいアナリティクスのタブを開く
- タイプに One-Way ANOVA(分散分析) を選択
- 目的変数に 給料、説明変数に 婚姻ステータス を選択
- 「実行」ボタンをクリック
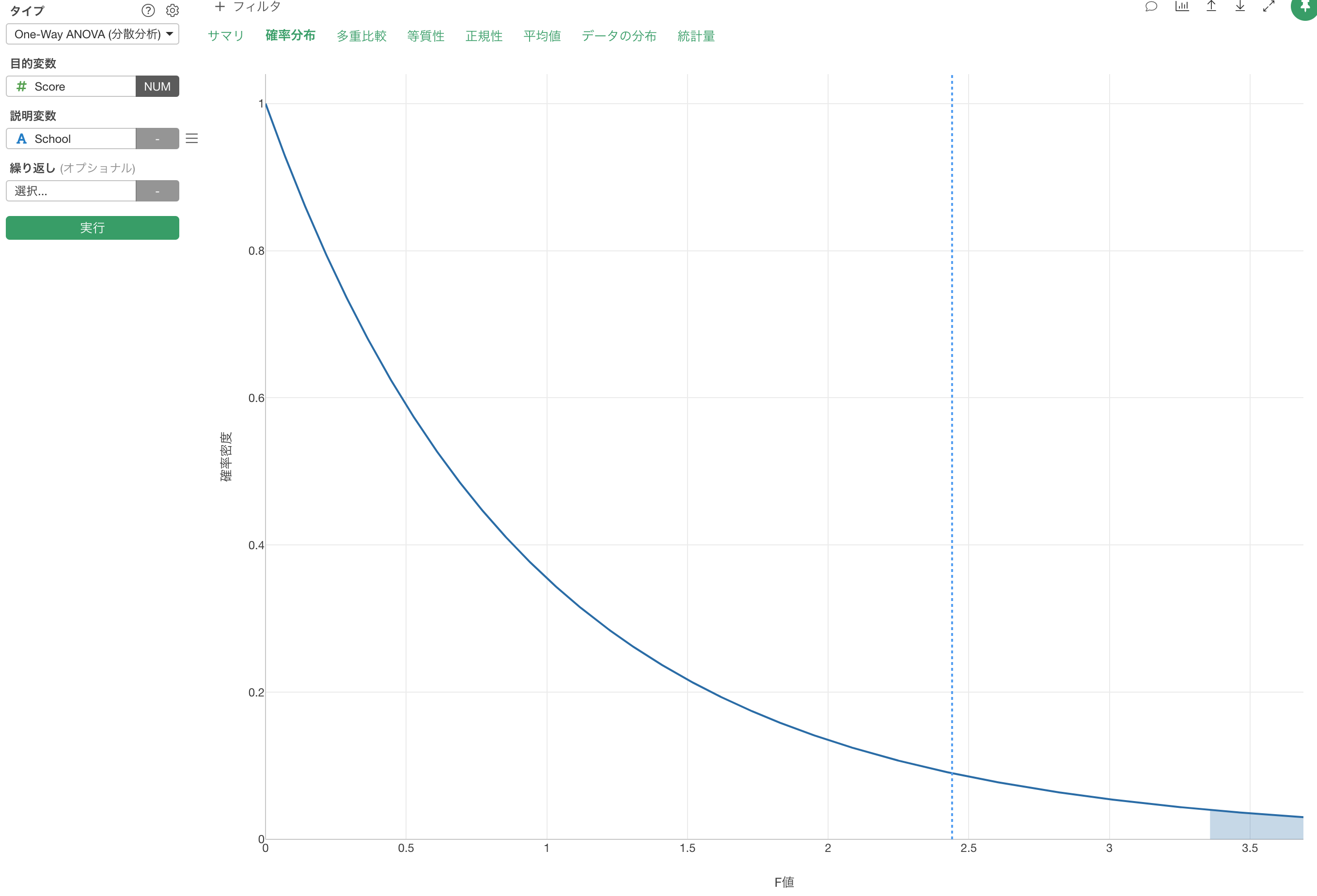
ExploratoryでANOVA検定を実行すると、デフォルトの設定では、各グループのばらつきの大きさが同じだと仮定(等分散を仮定)できない場合に使える「ウェルチのANOVA検定」が使われます。そのため、単純にグループ間2乗平均(婚姻ステータス)とグループ内2乗平均(残差)の比率を求めても、F値にはなりません。こちらについては、後ほどウェルチのANOVA検定のセクションで詳しく説明します。
今回は一度、ウェルチではなく、解釈しやすい通常のANOVA検定に切り替えましょう。
- 「設定」より「等分散を仮定」に「FALSE」を選択
- 「適用」ボタンをクリック

すると、「サマリ」セクションの下にANOVA検定の結果を示すいくつかの指標を確認できます。

結論から言うと、P値が約0.28%(0.002789…)であるため、有意水準5%の下、婚姻ステータスによる給料の平均の差は統計的に有意だと言えます。
こちらの表の1行目は、グループ間の平均のばらつきに関する情報で、2乗和の列はグループ内2乗和、2乗平均の列は2乗和の値を自由度で割ったグループ間2乗平均となります。
2行目はグループ内のばらつきに関する情報で、こちらも同じくグループ内2乗和、グループ内2乗平均を確認できます。
最後の行は、全体のばらつきに関する情報で、全体2乗和を確認できます。この値は、グループ間2乗和とグループ内2乗和を足し上げた値となります。
F値は、グループ間2乗平均(1行目)をグループ間2乗平均(2行目)で割った値となります。