生徒：ｔ検定の時にはグループ間でばらつきの大きさが同じだという仮定が成り立たない場合は、ウェルチのｔ検定を使うべきだという話がありました。ANOVA検定の場合にはこうした前提はないのですか？

先生：鋭いですね。実はANOVA検定にもそうした前提はあります。そしてANOVA検定にもウェルチのANOVA検定というものがあるのです。それでは、ANOVA検定における前提を整理した後に、ウェルチのANOVA検定の話をしていきましょう。

ANOVA検定の前提条件

ｔ検定のときにも触れましたが、ANOVA検定にも前提条件というものが以下の3つあります。

独立性
正規性
等質性

1つ目は独立性と言われるもので、全てのデータの行に当たるものは独立しているというものです。例えば、学校の成績のデータであれば生徒それぞれ、従業員データであれば従業員それぞれが独立しているということです。もし生徒によっては2回、3回と何度もテストを受けていて、そうしたデータが混ざっているのであれば、それぞれの行は独立しているとは言えません。この前提が満たされていないのであれば、データの取り方を変えたり、すでにあるデータを加工することで1行がそれぞれの生徒となるように調整する必要があります。

実験によっては全ての行が独立していないようにデザインされている場合もあります。例えば複数の学校の生徒たちがある特定の対策を行った前と後でどのように成績に変化があるか、といったものです。こうした実験により得られらデータに対しては「繰り返し測定の分散分析（ANOVA Test with Repeated Measure）」というタイプのANOVA分析の手法があります。（この本では触れません。）

2つ目の前提は正規性で、元のデータが正規分布しているというものです。これはデータの量がある程度あれば、中心極限定理によってサンプル平均の分布は正規分布となるため問題ないのですが、データ量が少ない場合には元のデータが正規分布していないと、サンプル平均の分布も正規分布に近似すると仮定できなくなるため、注意が必要です。

この場合は、こうした前提のない検定手法を使うことになります。そうした検定手法の代表的なものがクラスカル・ウォリス検定と呼ばれるものですが、こちらは次の節で紹介します。

そして最後の3つ目の前提が「分散の等質性」と言われるもので、複数のグループのばらつきが同じほどであるというものです。ｔ検定の場合には、もしこの前提が満たされていない場合はウェルチのｔ検定を使うという話をしました。

ANOVA検定においても、ばらつきの大きさが同じほどであるという前提を満たされない場合は、ウェルチのANOVA検定を使うことになります。ウェルチのANOVA検定では、ばらつきの等質性においてはグループ間でばらつきの大きさが違うということを考慮に入れた上でF値を計算します。

ウェルチのANOVA検定

それでは、ウェルチのANOVA検定では、それぞれのグループのデータ量の違いやばらつきの違いを重みとして加えた上で、グループ間の平均のばらつきの和とグループ内のばらつきの和の比率であるF値を計算します。

これまでのANOVA検定ではF値を以下のように計算しました。

\[\begin{aligned} F値 = \frac{グループ間の平均のばらつき}{グループ内のばらつき} \end{aligned}\]

まず分子の部分となるグループ間の平均のばらつきですが、これは元々データ量という重みを付けた上で計算されていたものです。これに対してウェルチのANOVA検定においては、さらにそれぞれのグループのばらつきの大きさという重みもつけます。ばらつきの小さいグループはより信頼できるという前提のもと、そうしたグループに対して相対的により大きな重みをつける補正を加えます。

次に分母の部分となるグループ内のばらつきですが、これはグループ間でのばらつきが等しいと言うことを前提としていたため、単純にそれぞれの値とグループ平均と差の2乗を足し上げました。しかし、もしこの前提が成り立たないのであれば、ウェルチのｔ検定で見たようにグループ間のデータ量にも差がある場合には歪みが生じます。そこで、この歪みを解消するために、ウェルチのANOVA検定ではデータ量（例えば生徒数）がより多いグループのばらつきにはより大きな重みをつける、といった補正を加えます。

こうして補正されたグループ間の平均のばらつきの和とグループ内のばらつきの和の比率としてF値を計算することになります。

\[\begin{aligned} ウェルチのF値 = \frac{重み付けされたグループ間の平均のばらつき}{重み付けされたグループ内のばらつき} \end{aligned}\]

こうしてF値が算出されれば、ここからは普通のANOVAといっしょです。F分布という確率分布を使ってこのF値かそれ以上に大きい値が得られる確率をP値として算出し、有意性を判断します。これがウェルチのANOVA検定です。

ｔ検定のときもそうでしたが、ウェルチのANOVA検定はばらつきの同質性という前提がありのときでもなしのときでも使えるので、一般的にはこちらのANOVA検定がよく使われます。

Let’s do it!

それでは、前節で見た従業員データの「給料」と「婚姻ステータス」の関係を調べるために行ったANOVA検定をもう一度見直してみましょう。これまでは、「給料」と「婚姻ステータス」の間には統計的に有意な関係があるということがわかっています。

しかし、ANOVA検定の前提を満たしているのでしょうか。3つの前提のうち1つ目の独立性については、今回のデータは従業員一人一行のデータであるため、満たしているとします。

残りの正規性と等質性の前提は、ANOVA検定の一部としてそれぞれのチェックが行われています。

正規性の前提チェック

2つ目の正規性の前提ですが、こちらは「正規性」というタブの下でシャピロ・ウィルク検定手法の結果を確認することができます。

この本では「シャピロ・ウィルク検定」の詳細については触れませんが、簡単にいうと、帰無仮説が「目的変数のばらつきの分布の形は正規分布である」という前提のもと、手元のデータのようなばらつきの分布の形をしている確率はどれくらいなのかというのがP値として算出されます。

ここでは、P値が限りなく0に近いため、「正規分布している」という帰無仮説を棄却できます。ということは「正規分布していない」ということです。「結果」の列を見ると正規性の前提は満たされていないことが記述されています。

「データの分布」タブを見れば視覚的にも明らかに正規分布でないことがわかります。

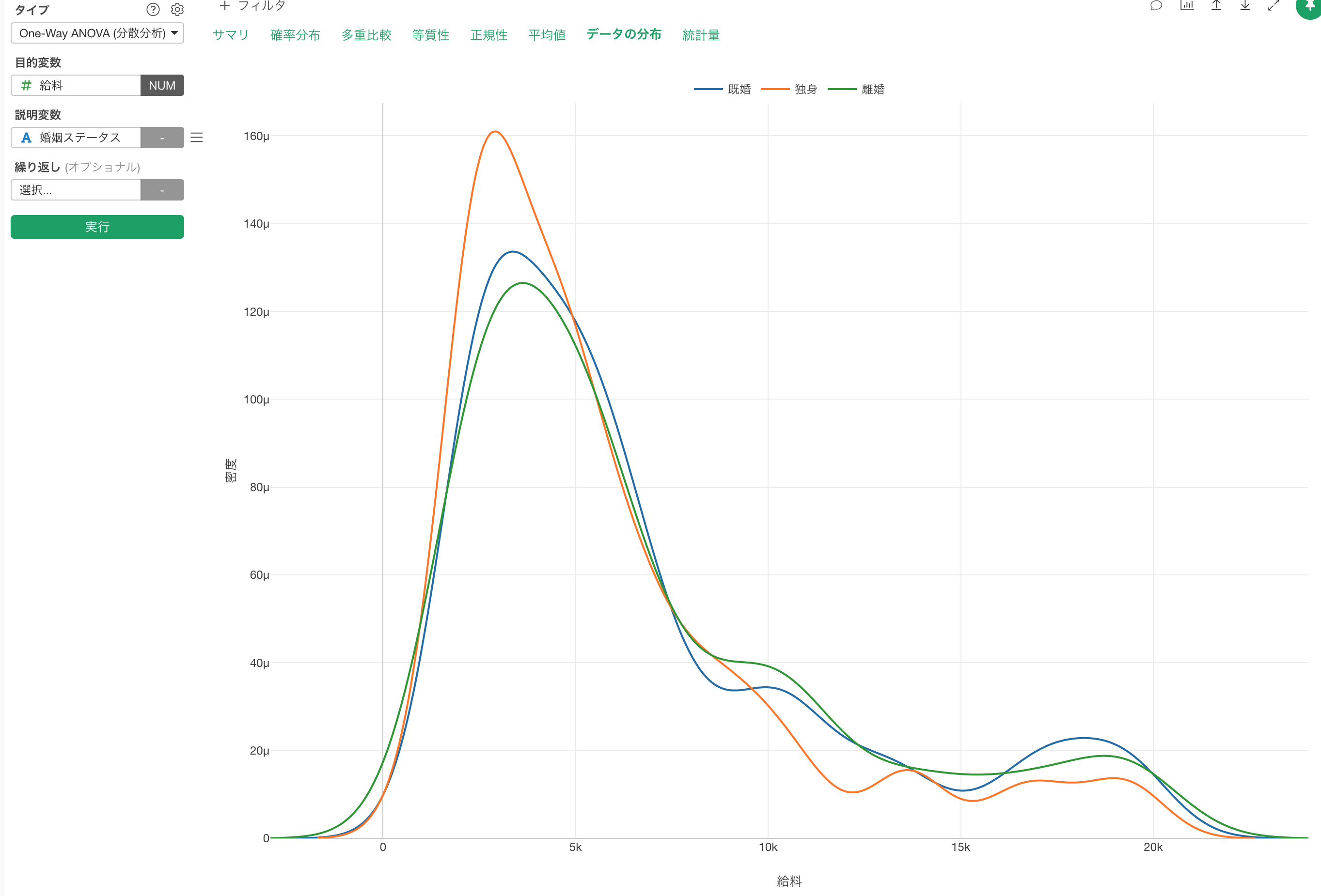
しかし、今回のデータは1470人分であるため、中心極限定理によってサンプル平均の分布は正規分布となることがわかっているため、これがANOVA検定が使えないということにはなりません。

等質性の前提チェック

もう1つの前提であるばらつきの等質性が満たされているかどうかについては、こちらは「等質性」というタブの下で確認することができます。

こちらはデフォルトでは「Brown-Forsythe Test（ブラウン・フォーサイス検定）という手法を使って全てのグループのばらつきが同程度かどうかの検定が行われます。こちらの検定手法についてもこちらの本では詳細については触れませんが、簡単にいうと帰無仮説が「すべてのグループのばらつき（分散）が同じである」という前提のもと、手元のデータにおけるグループ間のばらつきの違いが起きる確率はどれくらいかというのがP値として算出され、その値の大きさによって帰無仮説を棄却できるかどうかを判断します。

ここでのP値は約4.1%であるため、有意水準が5%の元では「すべてのグループのばらつき（分散）が同じである」という帰無仮説を棄却することができます。ということは、「すべてのグループのばらつき（分散）が同じでない」ということになりますから、グループ間のばらつきの等質性における前提が満たされていないことになります。これは「結果」の列でも記述されています。

また先ほど見たように、「データの分布」のタブの下でもグループ間のばらつきの大きさの違いを視覚的に確認することができます。

独身のグループは他の2つのグループに比べて給料が2000ドルから3000ドルにかけてにより多くの人たちが集まっていることが確認できます。この分布を表す密度曲線においては全てのグループの曲線の下の面積は同じですので、独身のグループの曲線の一部が他に比べて高いということは、ばらつきの大きさは他のグループに比べて小さいということを意味します。

これは「統計量」のタブの下で、独身グループの標準偏差の値が他の2つのグループに比べて小さいことでも確認できます。

しかし、ExploratoryではANOVA検定のデフォルトはウェルチのANOVA検定が使われています。本文でも述べたようにウェルチのANOVA検定はグループ間のばらつきの大きさが同じであるという前提はありません。そのため、こちらの等質性の前提が満たされているかどうかは問題とはなりません。

そこで、このANOVA検定の結果に対する判断が変わったり、それに対する信頼が揺らいだりすることはありません。

もし、何か特別な理由でウェルチのANOVA検定ではなく、等分散を前提とするANOVA検定を使いたい場合は、プロパティより「等分散を仮定」をTRUEにしてから実行することもできます。