Exploratoryの使い方 Part 4 - アナリティクス
このノートは、Exploratoryを効率的に使い始めることができるように作られた「Exploratoryの使い方」の第4弾、「アナリティクス」編です。
Exploratoryには様々なアナリティクスの機能があります。その中でも今回は相関分析、予測モデルを使った分析、自由記述の回答に対するテキスト分析を実際にExploratoryを使いながら行っていただくことで、アナリティクスに関する基礎的な使い方を体験していただければと思います。
所要時間は20分ほどとなっています。
それでは、さっそく始めていきましょう！
1. データをインポートする
今回はサンプルデータとして以下の2つのデータを使用します。
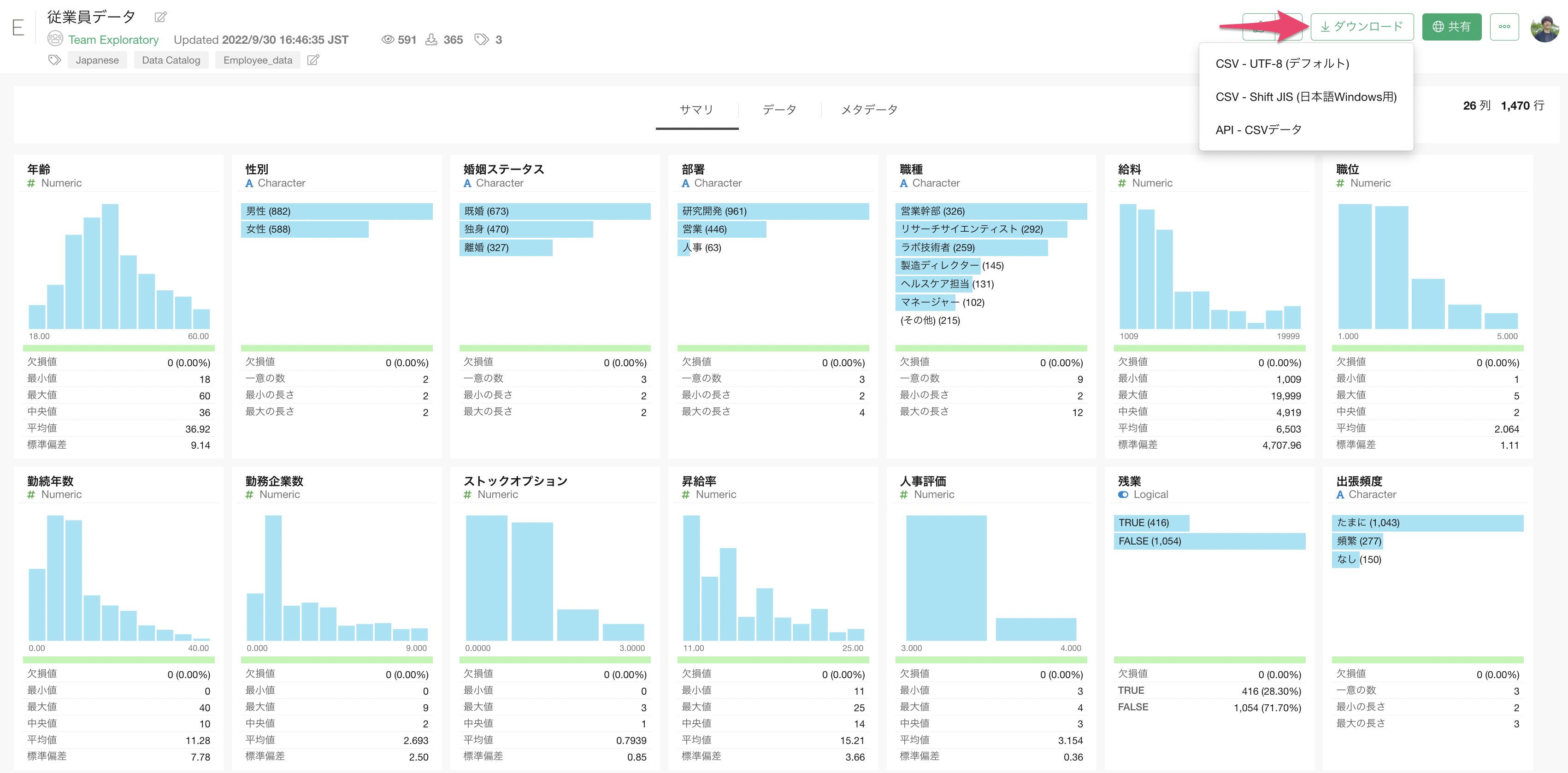
データはページの右上の「ダウンロード」ボタンからダウンロードできます。Macをお使いの方は「CSV-UTF8」を、Windowsをお使いの方は「CSV - Shift-JIS」をダウンロードしてください。
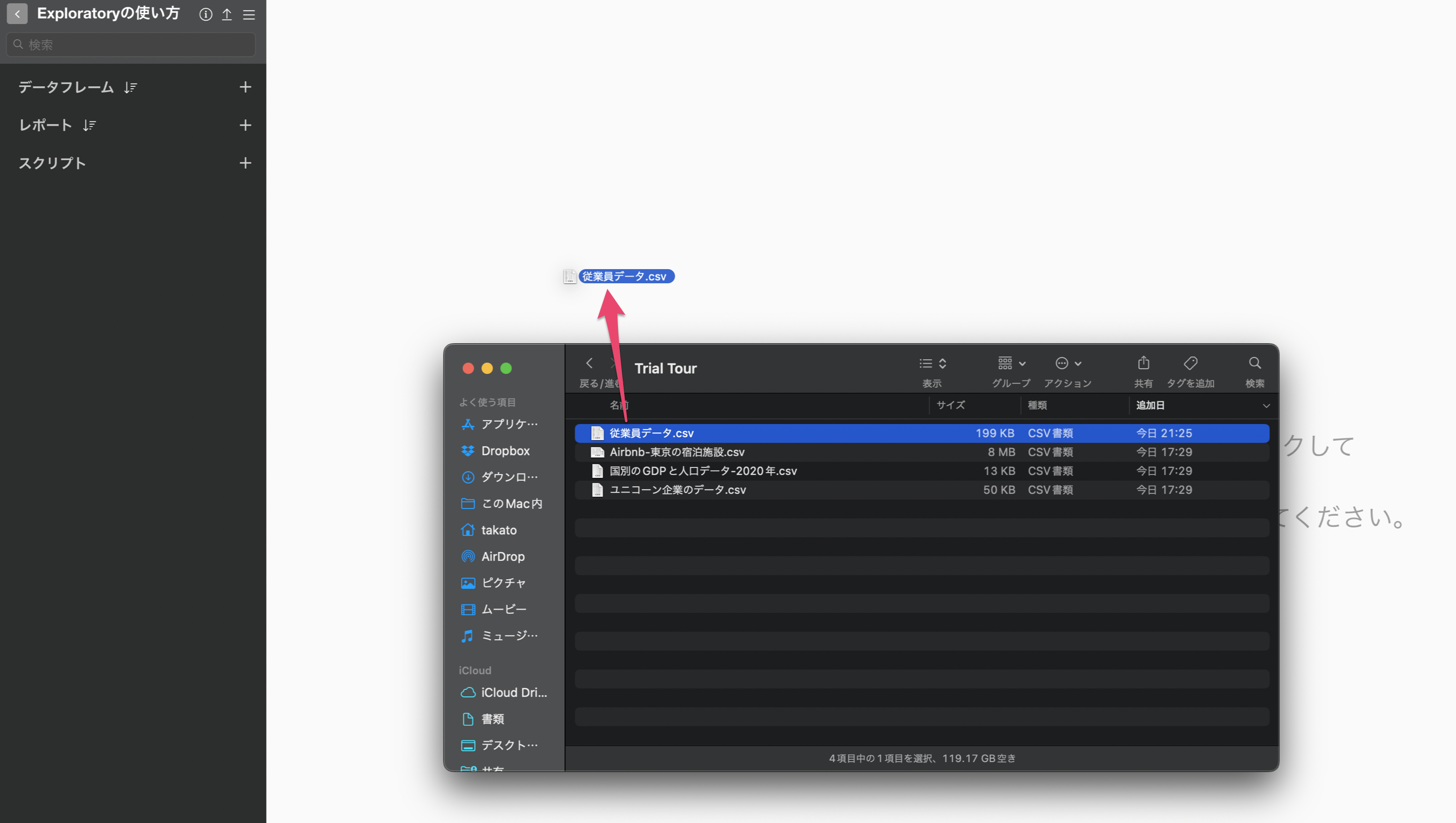
従業員データ、顧客満足度調査のデータをそれぞれダウンロードできたら、ダウンロードしたフォルダを開き、２つのCSVファイルをExploratoryの画面にドラッグ＆ドロップします。
ファイルの選択ダイアログが表示されるため「インポート」ボタンをクリックします。
インポートダイアログの左側にある項目から、インポート時の設定を行うことが可能ですが、今回は設定は不要なため「全てをOK」ボタンをクリックします。
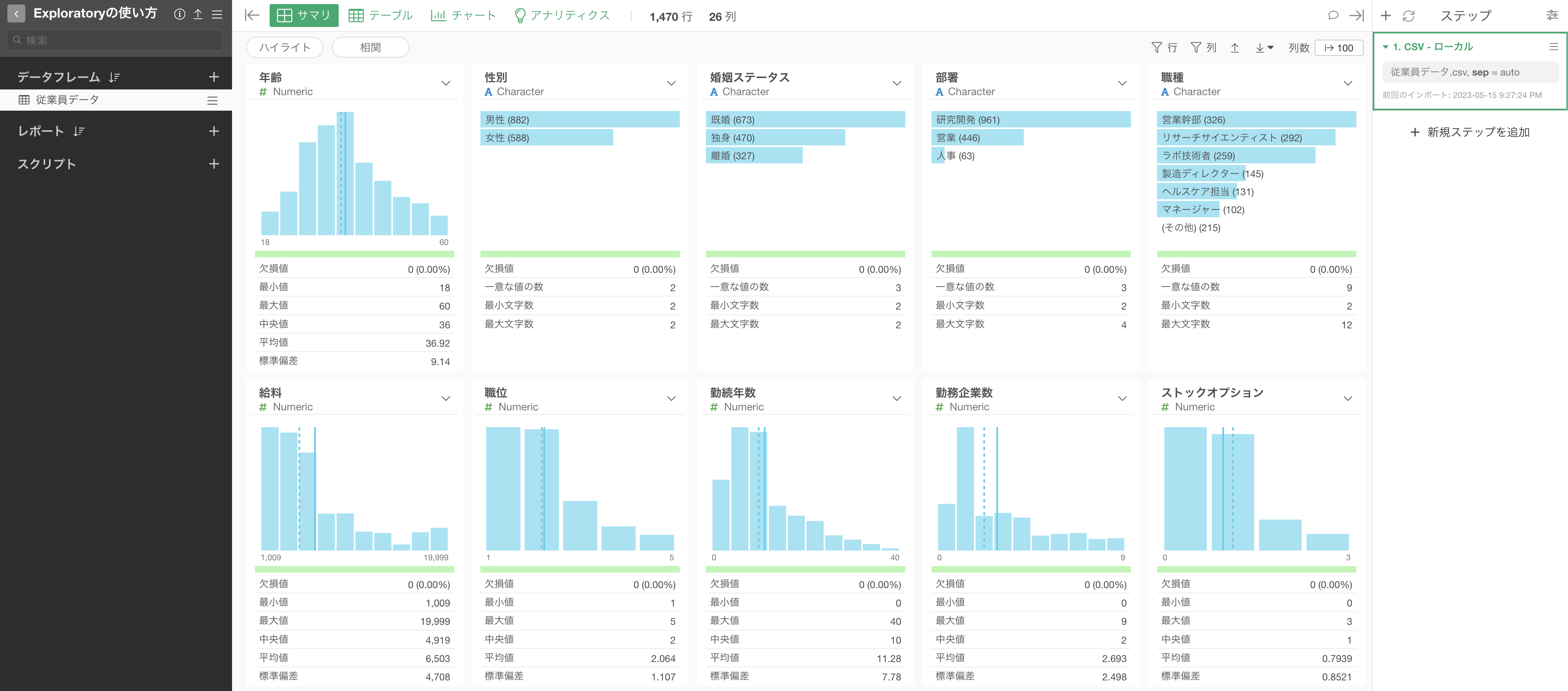
従業員データ、顧客満足度調査のデータをインポートすることができました。
2. 目的：給料に何が関係しているのか調べる
まず初めに、従業員の「給料」に関係のある要因を知りたいとします。
サンプルデータの従業員データを使って、従業員の給料には何が関係しているのかを調べるために、相関分析、さらに予測モデルを使った分析を簡単に行ってみましょう。
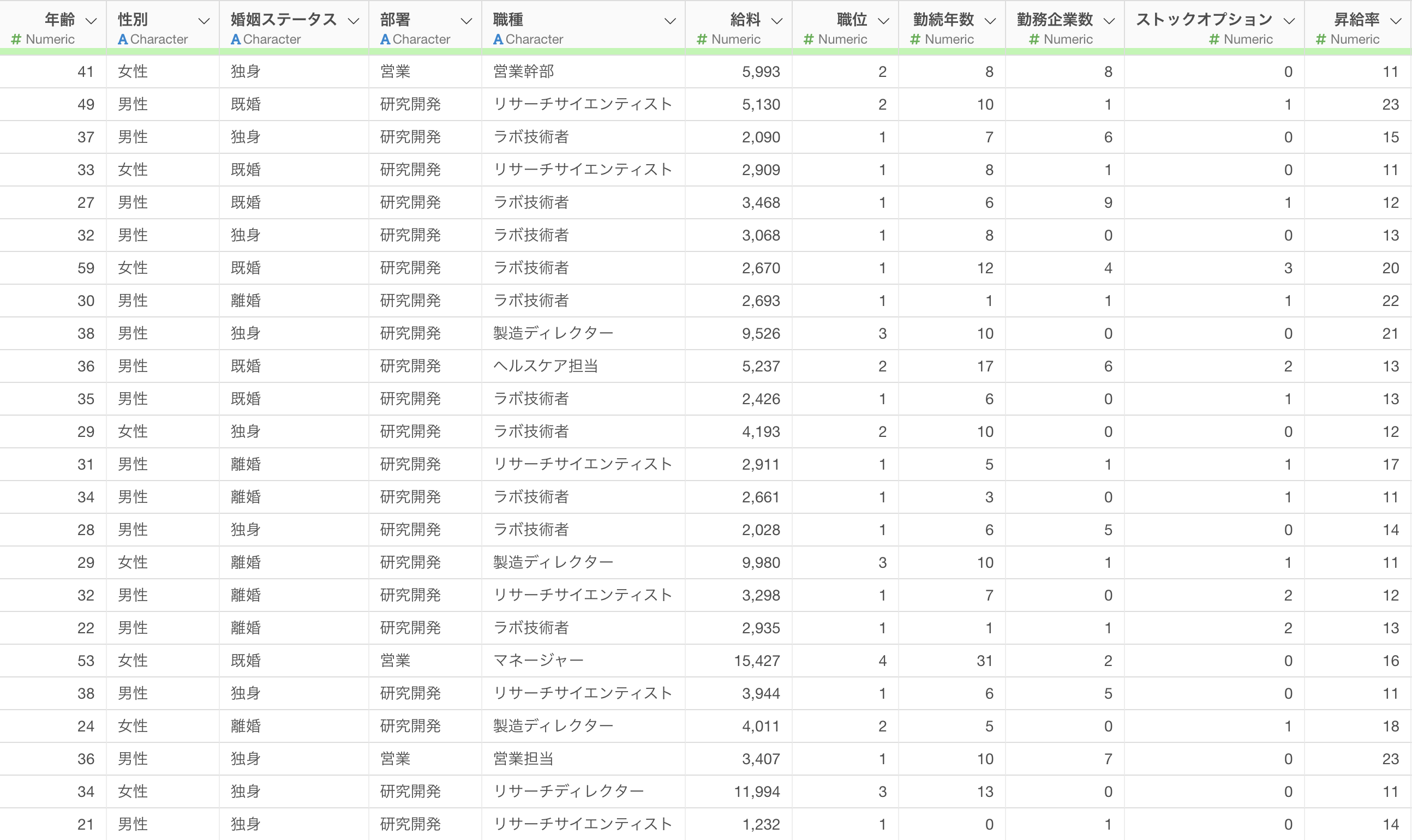
今回使う従業員データは1行が1従業員になっており、給料や勤続年数などの従業員に関する属性情報が列として入っています。
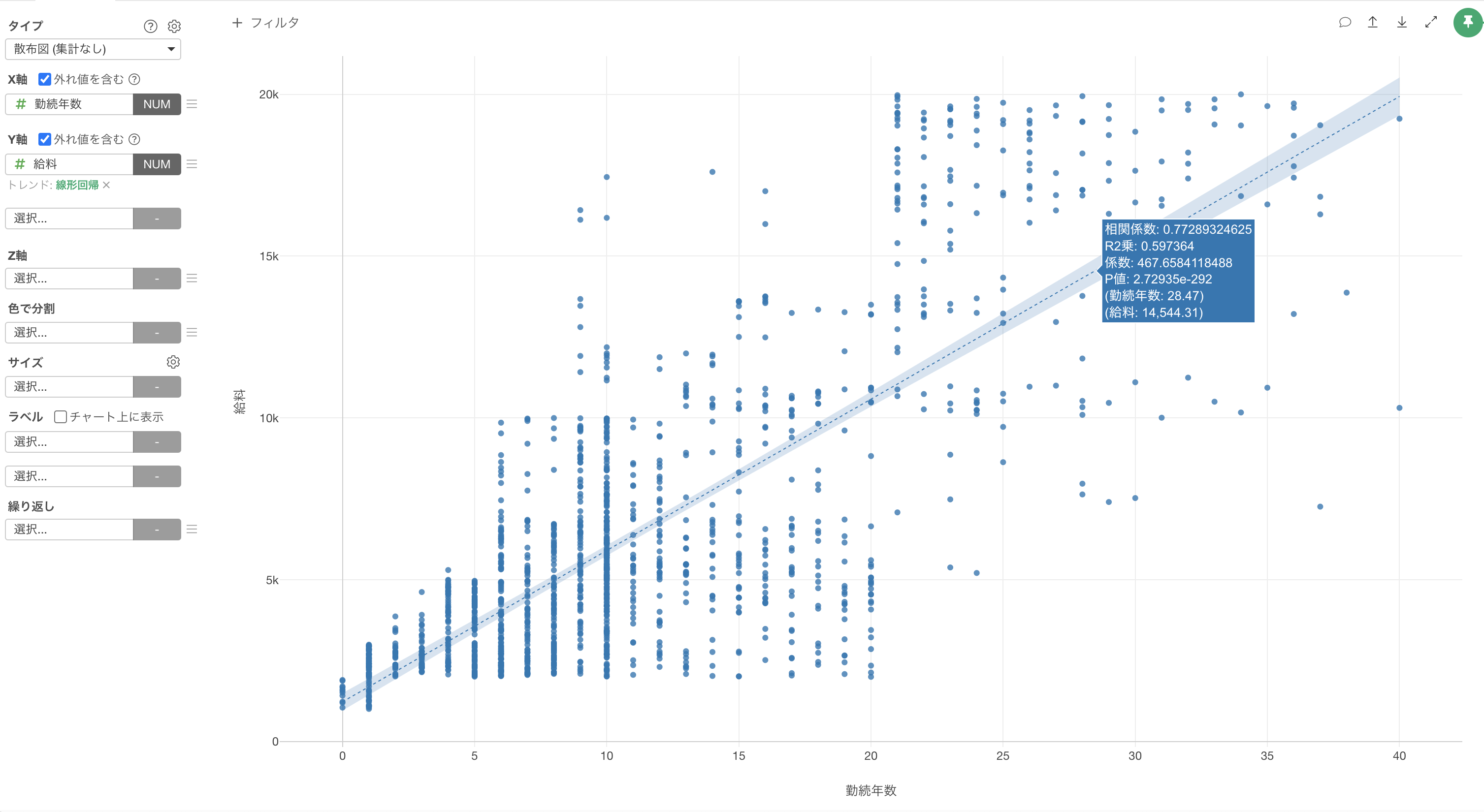
3. 相関を調べる
それでは、さっそく給料と相関関係のある変数はどれか、それはどのような関係なのかを調べていきましょう。
ちなみに、相関関係とは2つの変数のうち、1つの変数の値が変わるともう1つの変数の値も一定の規則を持って一緒に変わる関係のことを言います。
使い方ガイドの「可視化」編では、相関関係を可視化するために「散布図（集計あり）」を使いましたが、給料と全ての列の相関関係を調べるために散布図を一つずつ作成するのは大変な作業になります。
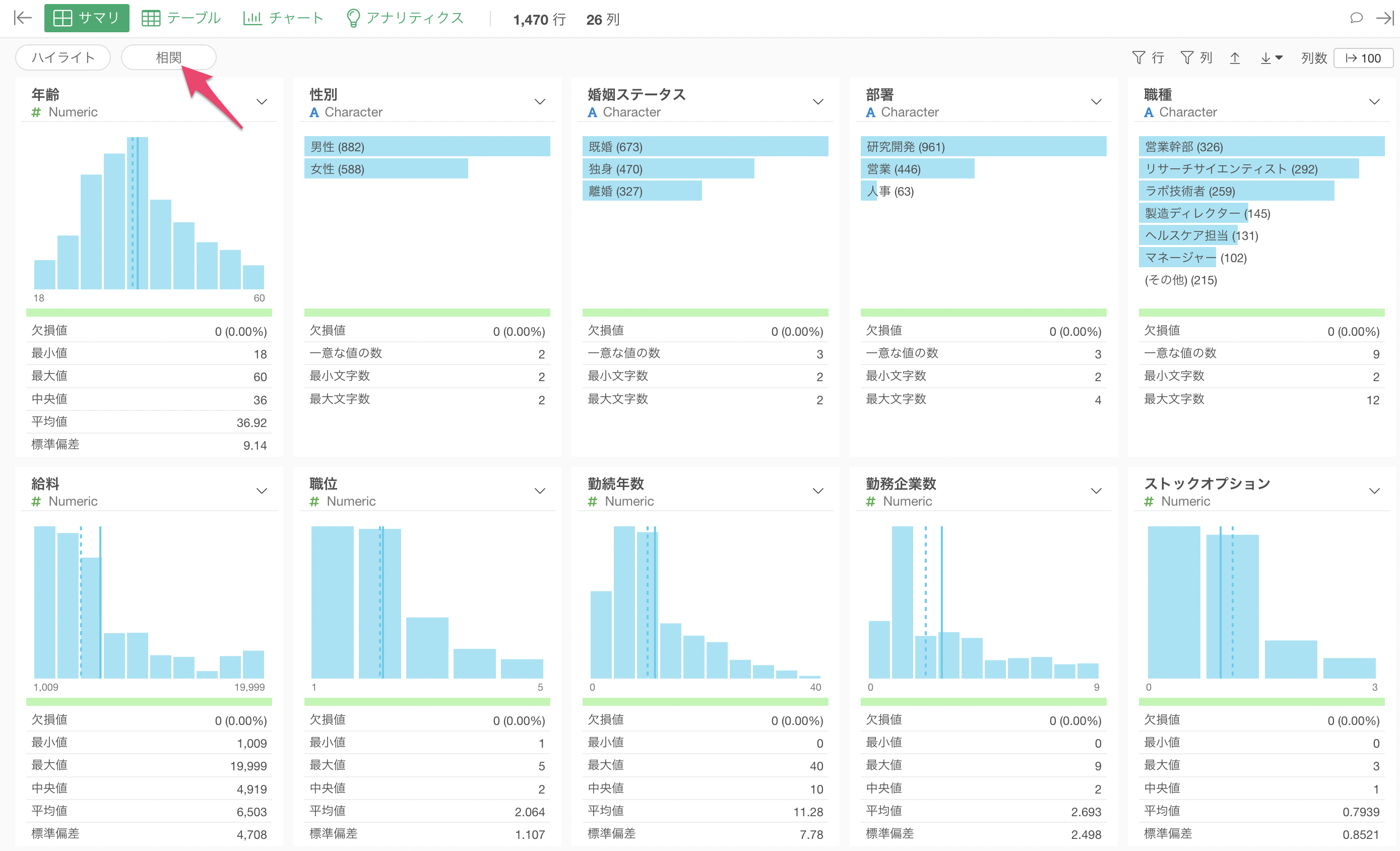
そこで今回は、Exploratoryのサマリビューの「相関」モードという機能を使って、給料と他の全ての変数との関係を一気に調べてみたいと思います。
サマリビューを開き、「相関」ボタンをクリックします。
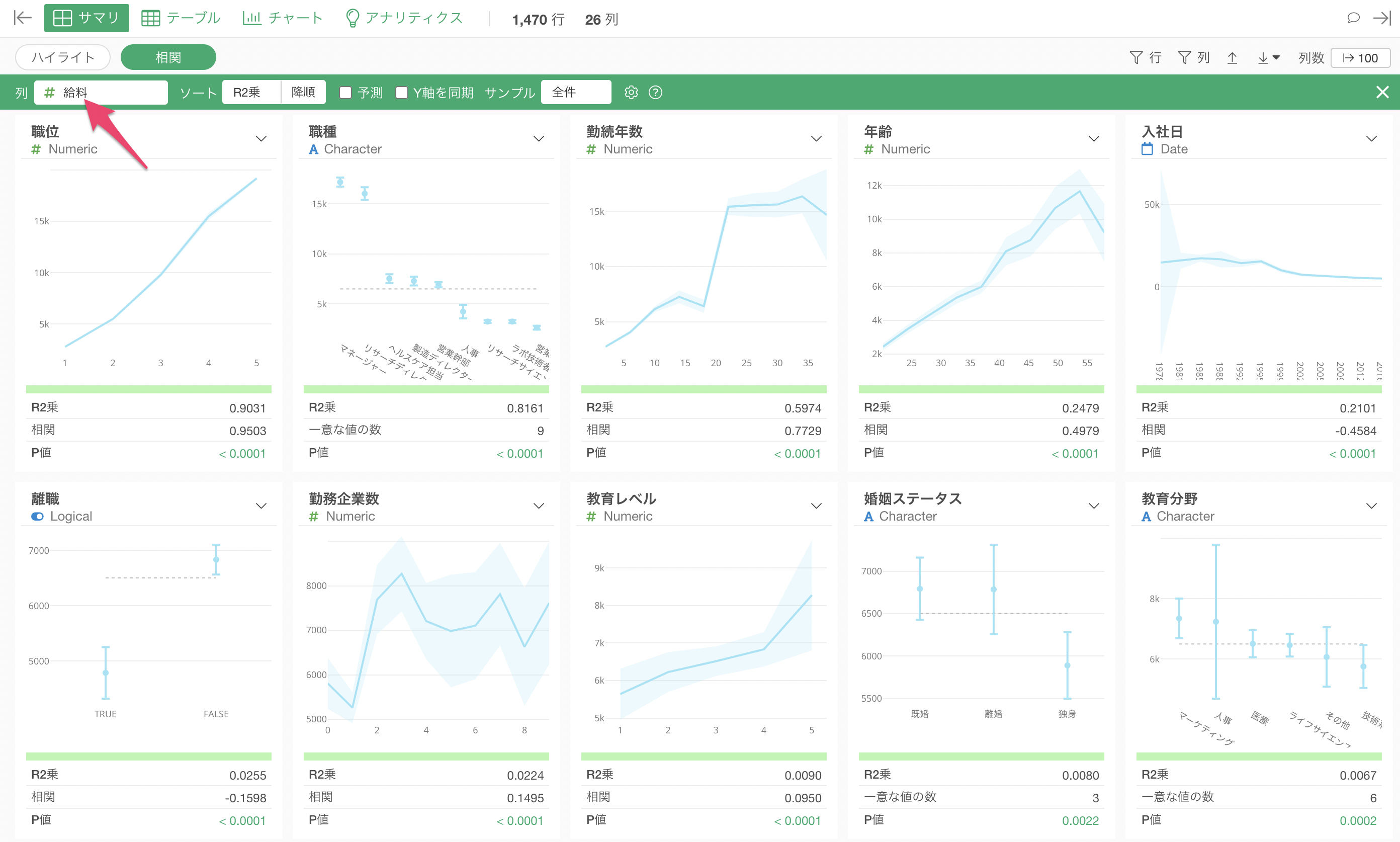
相関を見たい列に「給料」を選択します。
相関モードでは、データタイプに合わせてそれぞれの変数との関係を可視化したチャートと相関関係の強さを表す指標が一気に自動的に生成されます。
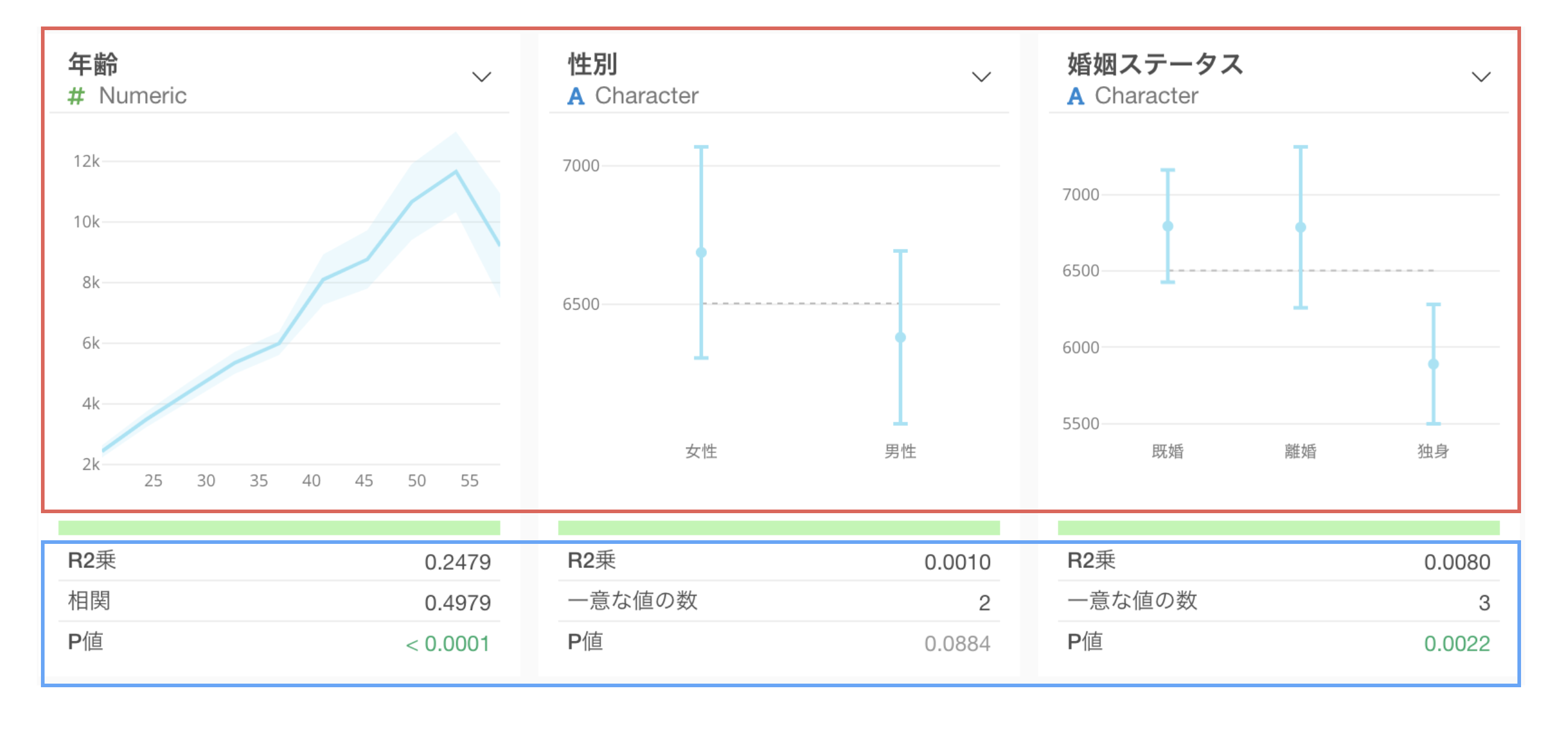
チャートの解釈
数値
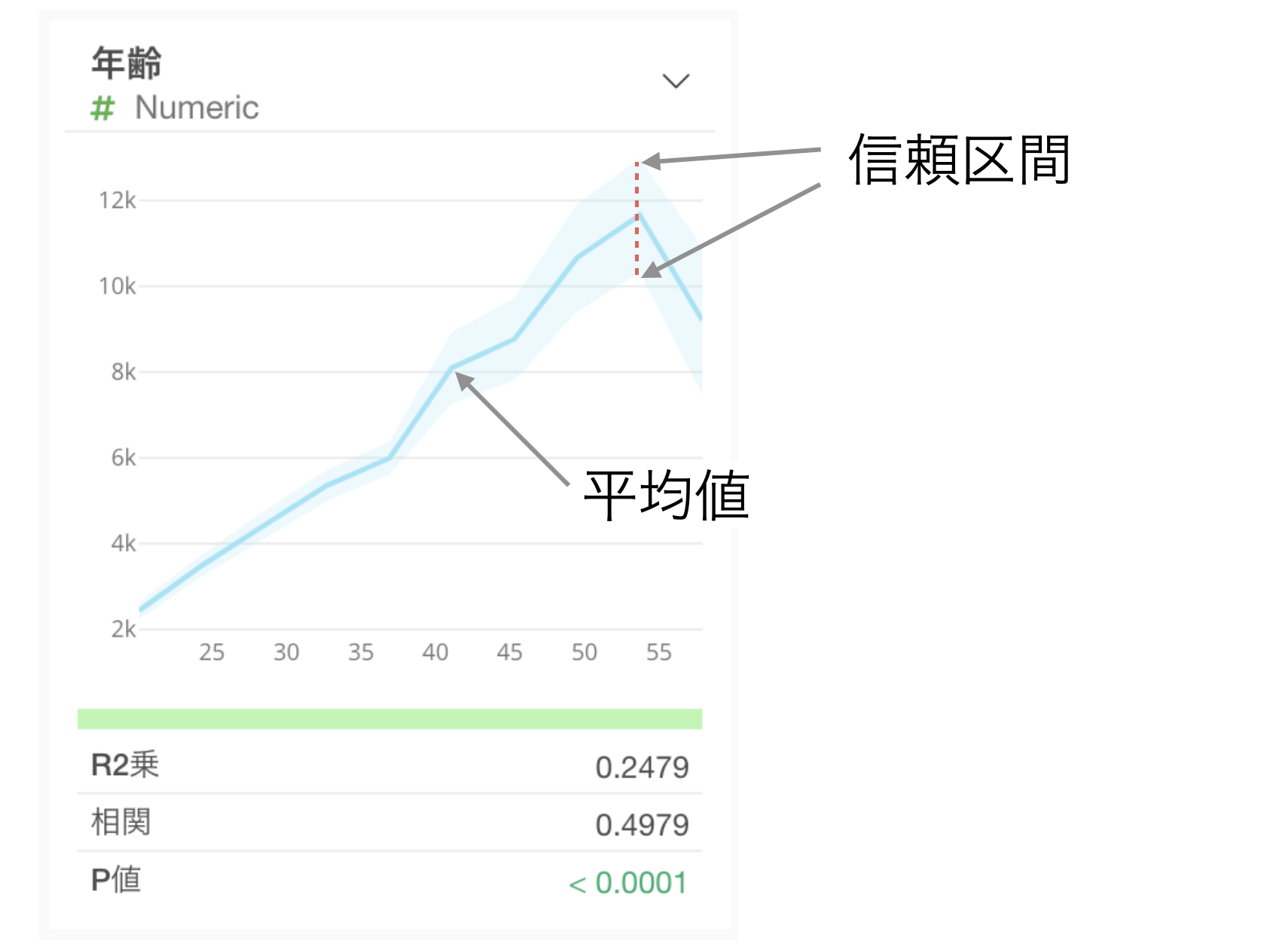
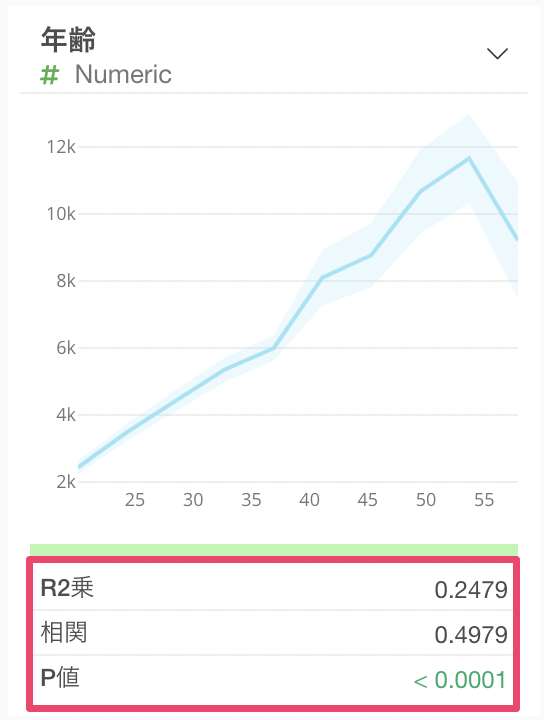
数値型の場合は値を等幅で10等分し、それぞれの区間における平均値がラインチャートとして可視化されます。薄い水色の区間は95%信頼区間になります。
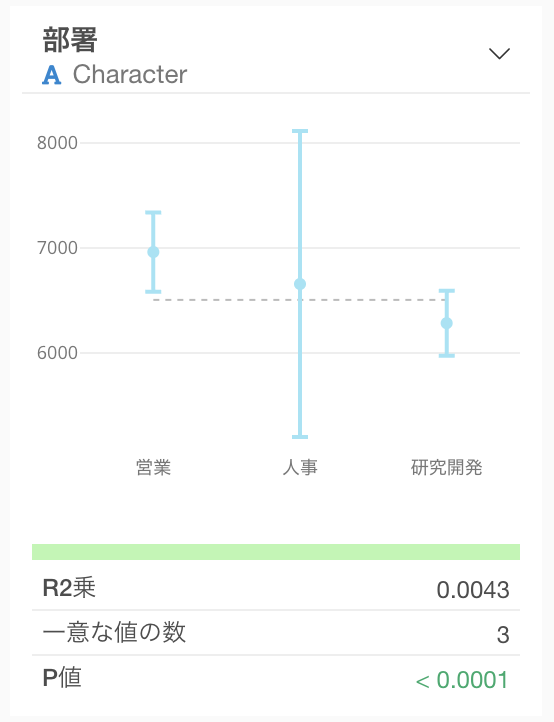
カテゴリー
カテゴリー型の場合は、それぞれのカテゴリーにおける平均値とその95%信頼区間がエラーバーとして可視化されます。
指標の解釈
相関の対象に数値型の列が選ばれている場合、それぞれの列には下記の指標が表示されます。
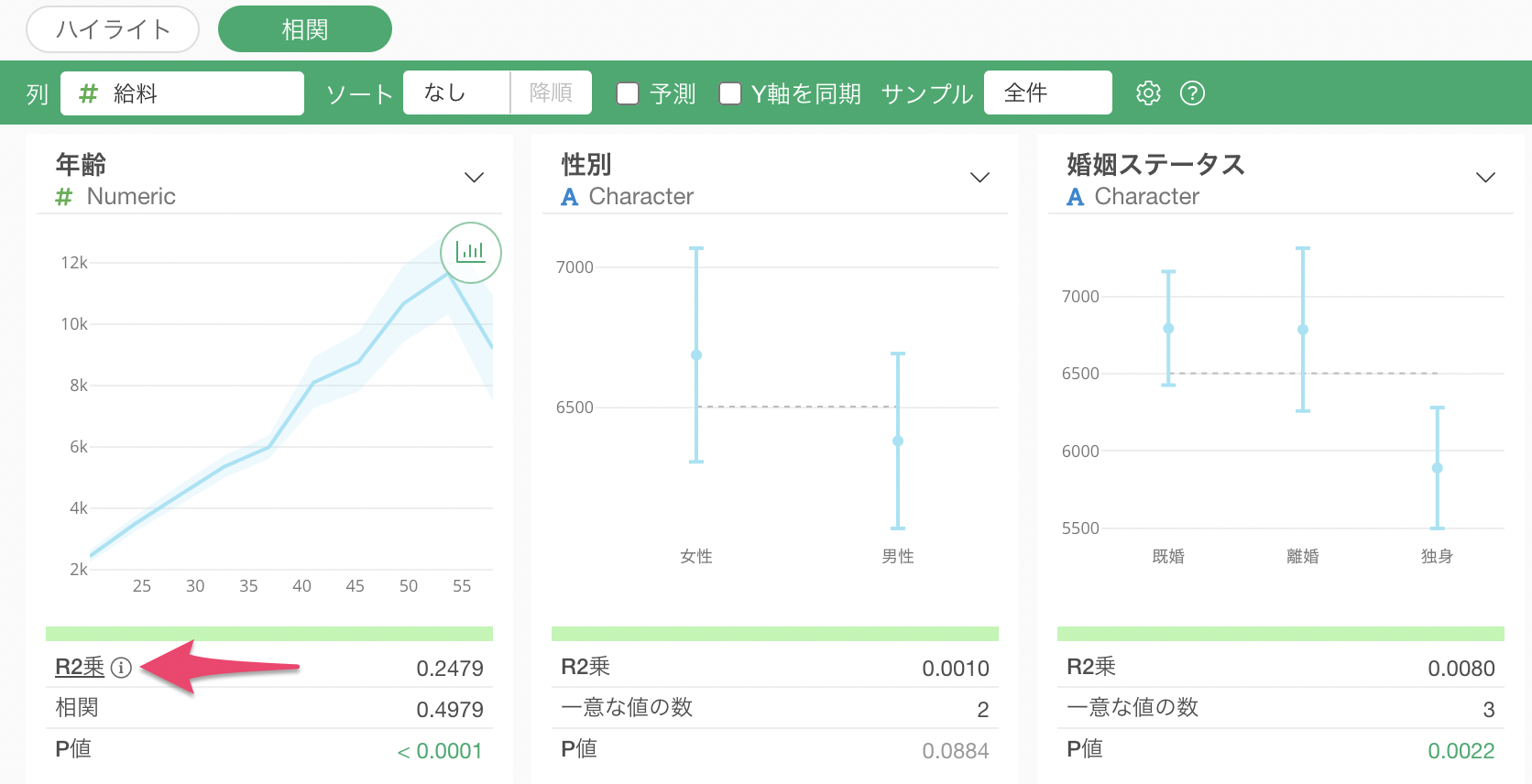
- R2乗：R2乗は目的変数の値のばらつきのうち、この変数によって説明される割合を示します。つまり、この2つの変数間の関係の強さを表しています。R2乗の値は相関係数の値を2乗した値と同じになります。値は0から1の間で、1が最も強い関係を示します。
- P値：P値は2つの変数の間には関係がないという帰無仮説（前提）を受け入れた場合に、ここで見られる何らかの関係が観察される確率を示します。一般的にはしきい値として0.05（5%）が使われ、その場合、それよりも低ければ有意とされる。
- 相関：相関係数は目的変数との相関関係の強さを表します。-1から1の間を取り、-1は最も強い負の相関、1は最も強い正の相関、0は相関無しとなります。
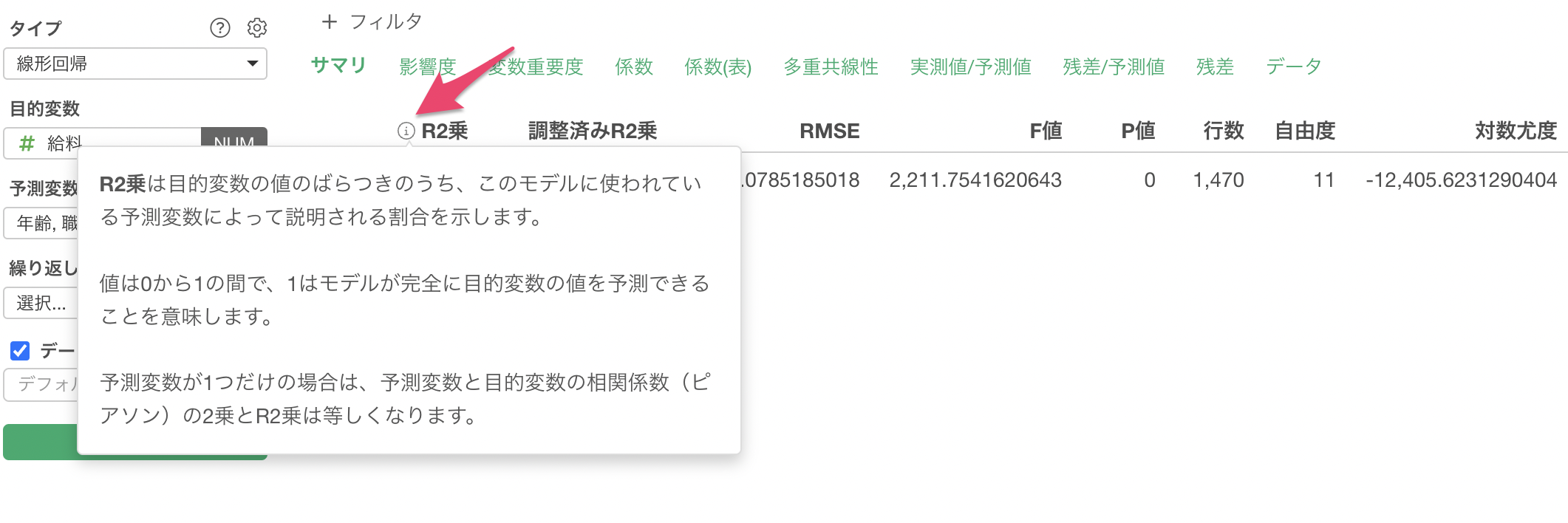
ちなみに、各指標の右横にある「i」を押すことで、指標の意味を確認できます。
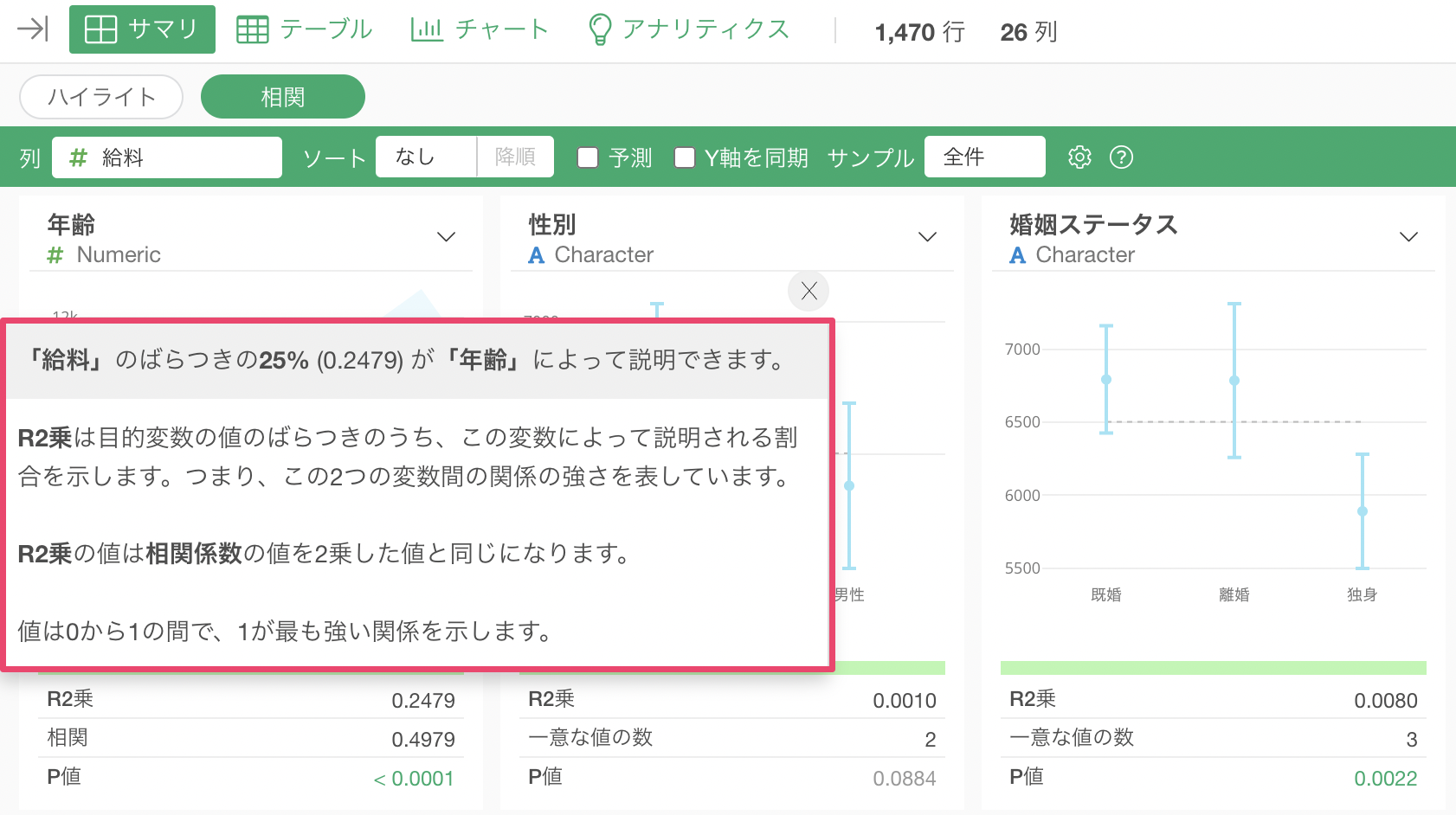
例えば、R2乗の指標の「i」を押すと下記のようにポップアップが表示され、指標の意味を確認することが可能です。
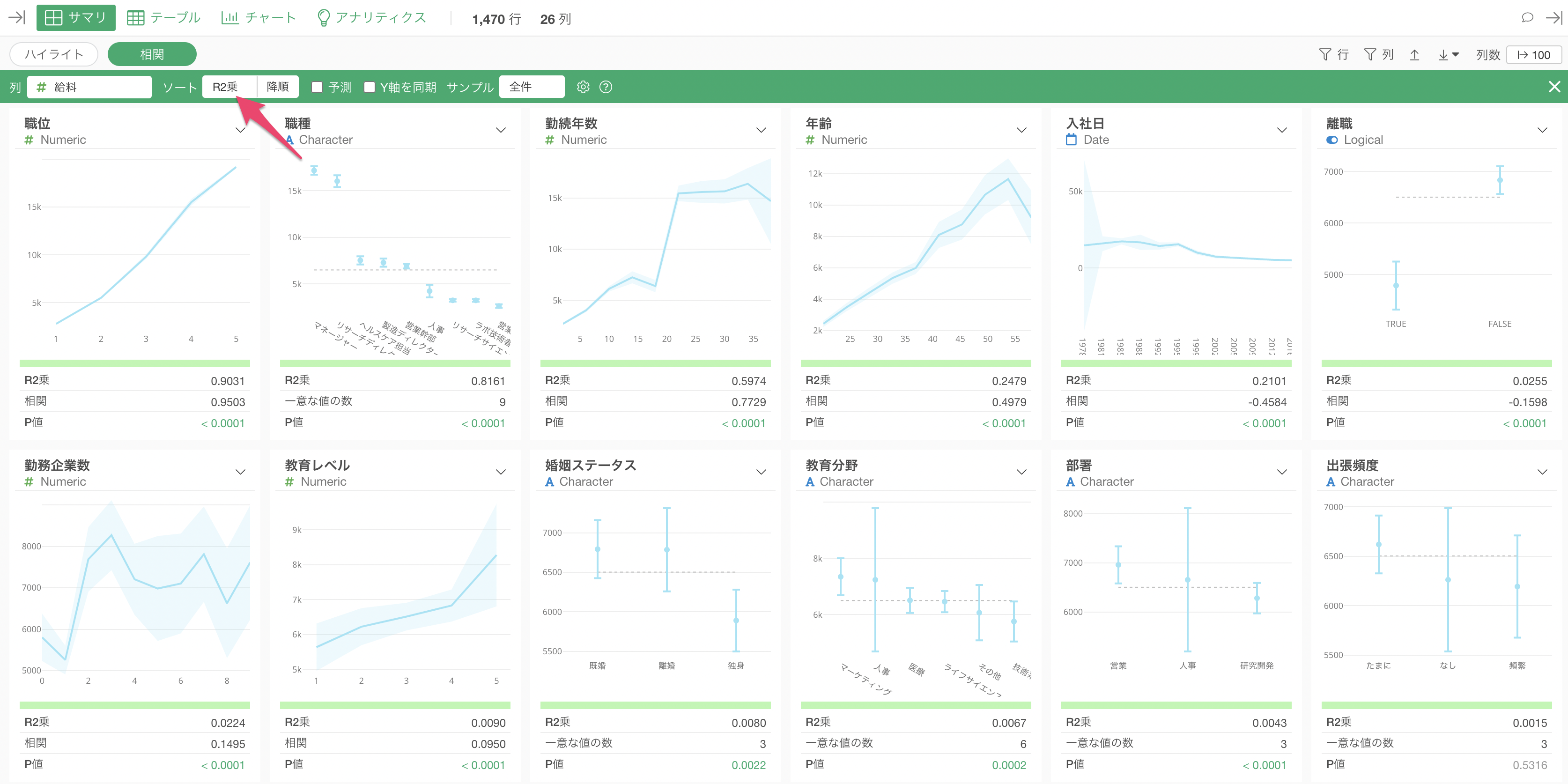
相関モードの結果を解釈する
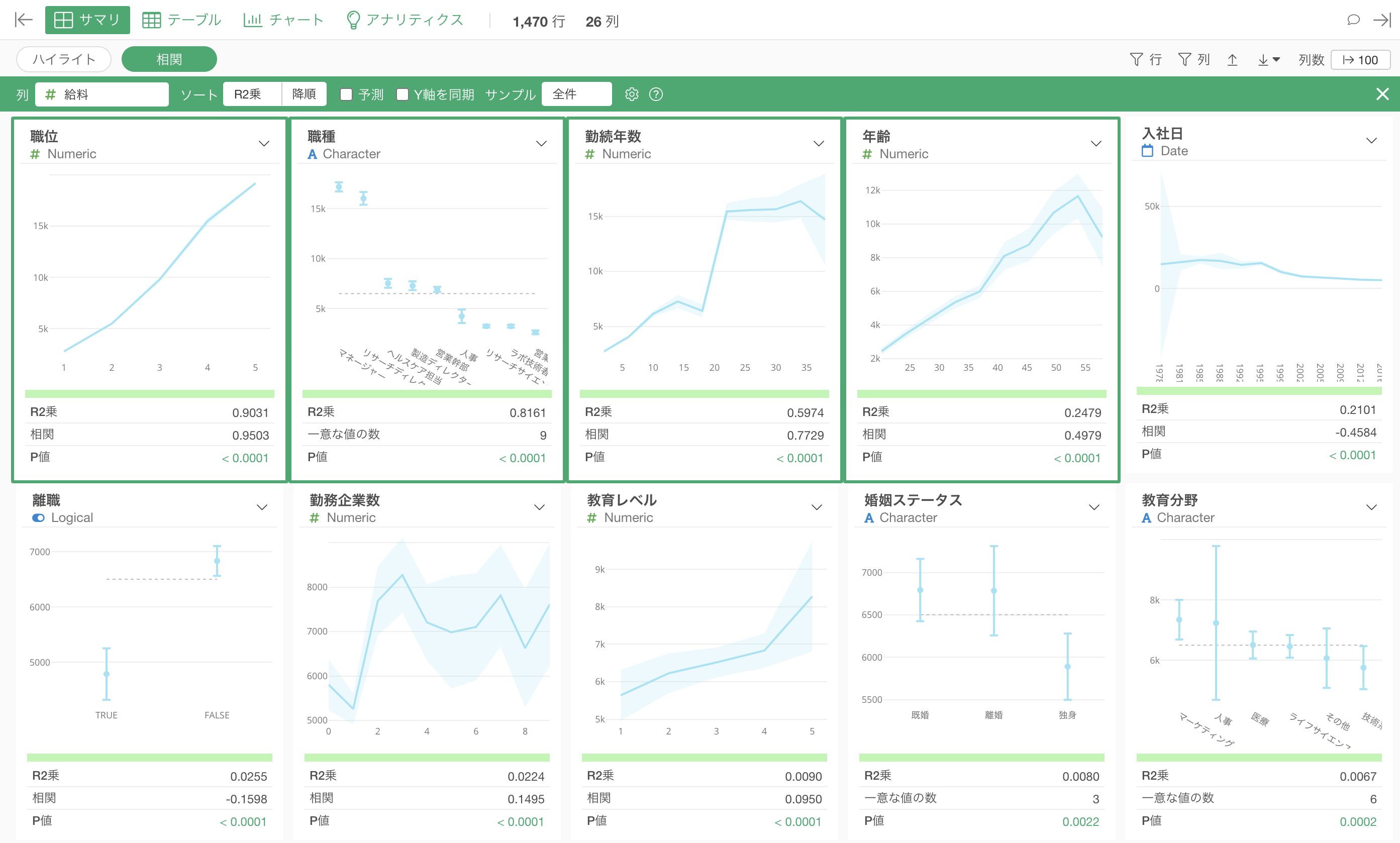
相関モードを使用したとき、デフォルトでは「R2乗」を使って相関の強い順に列がソート（並び替え）されています。
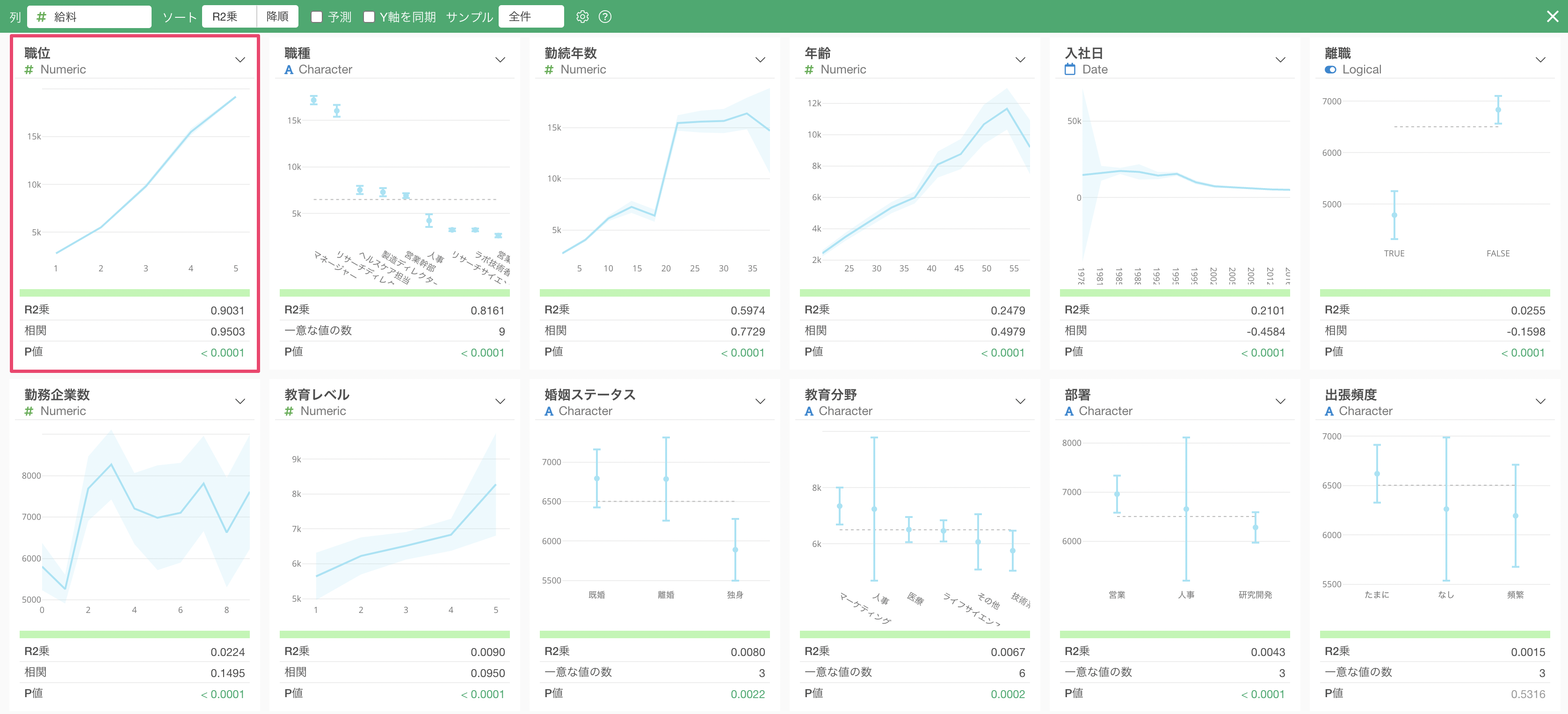
給料と最も相関の強い変数は「職位」で、チャートを見ると、「職位」が上がると「給料」の平均値も上がっていることがわかります。
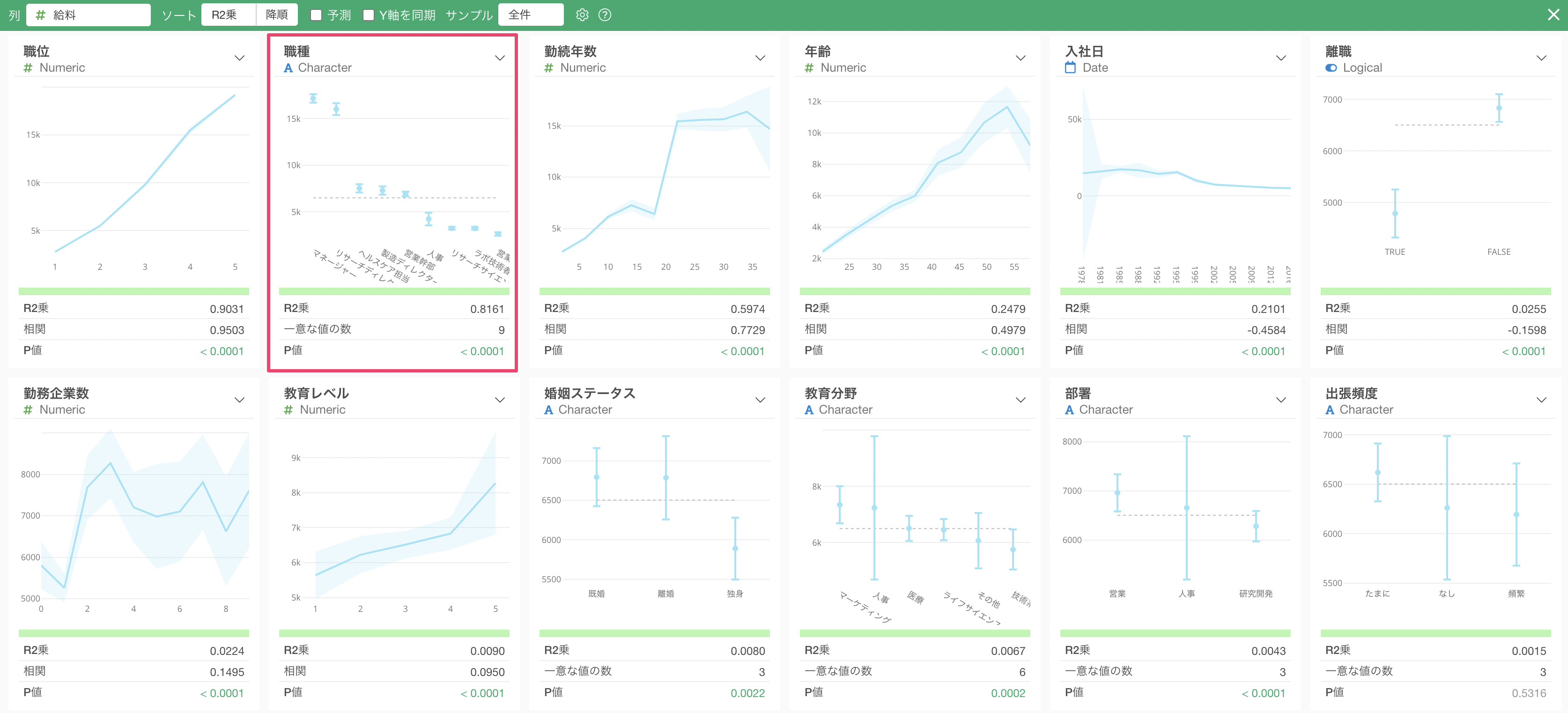
次に相関が強いのは「職種」で、チャートを見ると「マネージャー」や「リサーチディレクター」給料は他の職種に比べて高いのがわかります。
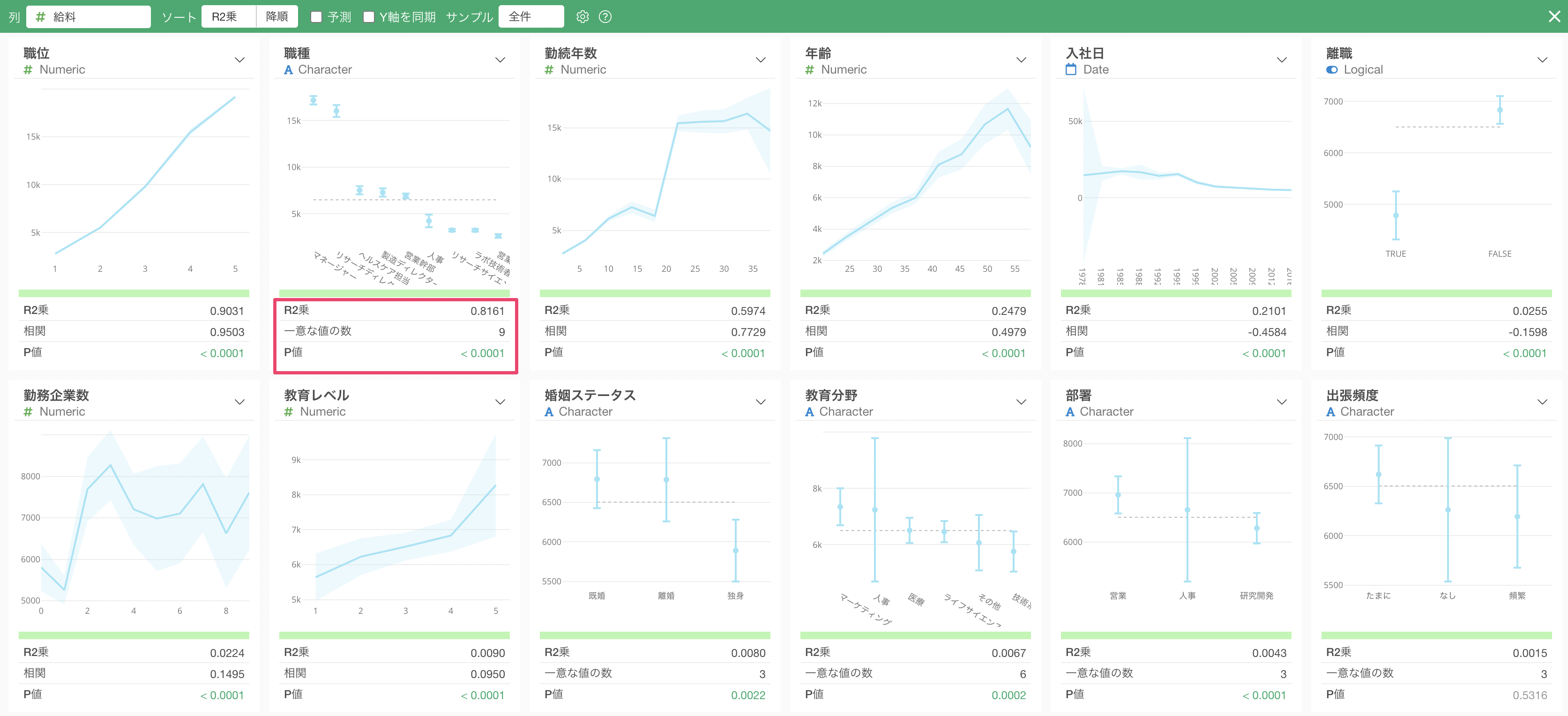
指標を見ると、R2乗は0.8161と相関がかなり高いのがわかりますが、先ほどの「職位」のR2乗である0.9301と比べると、そこまでは強くないことがわかります。
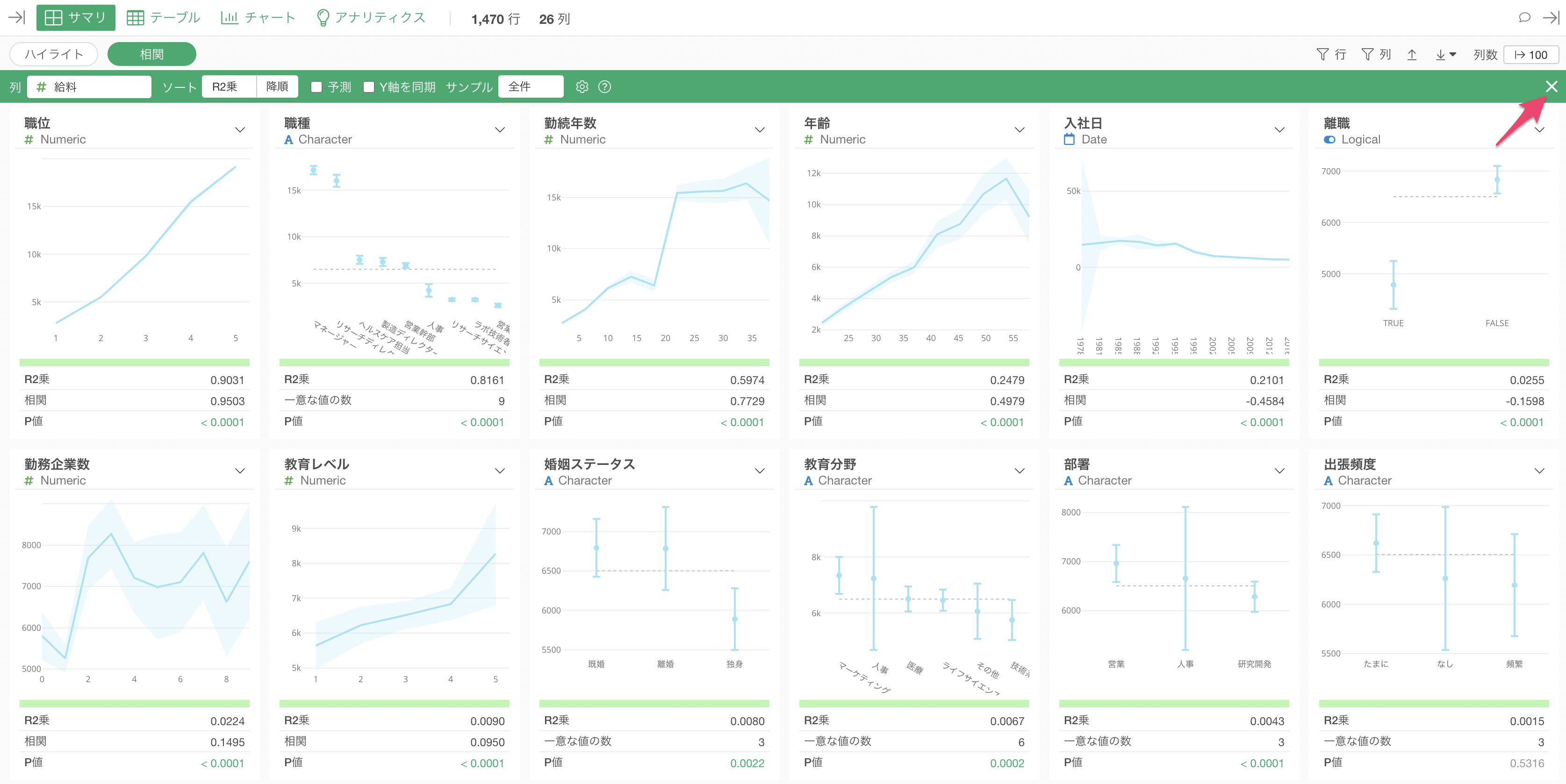
相関モードを終了したい場合、右上にある「×」ボタンをクリックします。
このように、「相関モード」を使って効率的に目的と他の全ての列との間の関係を一気に調べることができます。
相関モードの詳細については、こちらのセミナーでも紹介しておりますので、興味がある方はご覧ください。
4. 予測モデルとは？
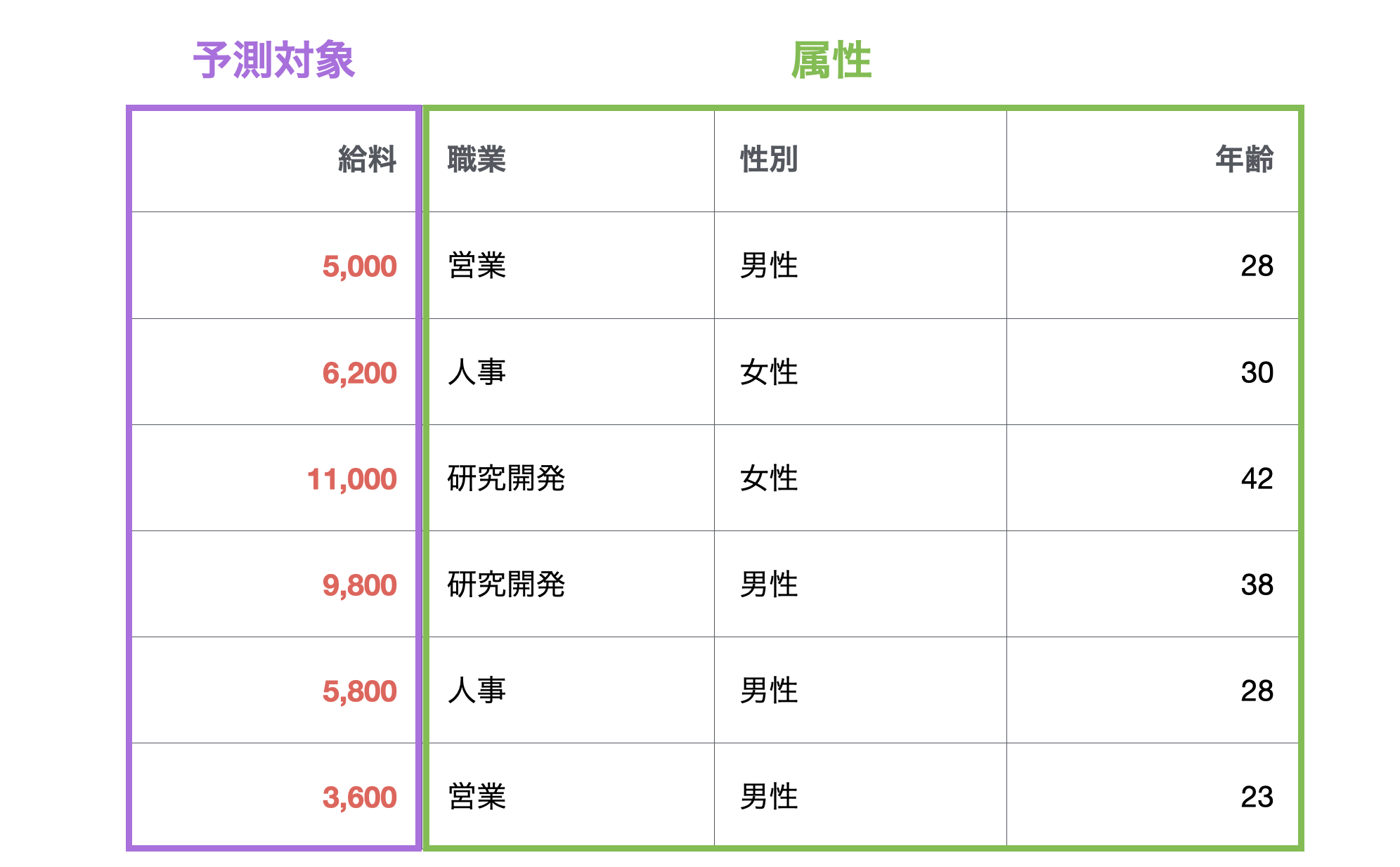
例えば、従業員ごとの給料データがあったとします。今回の予測対象は給料で、属性として職業や性別、年齢の列があります。
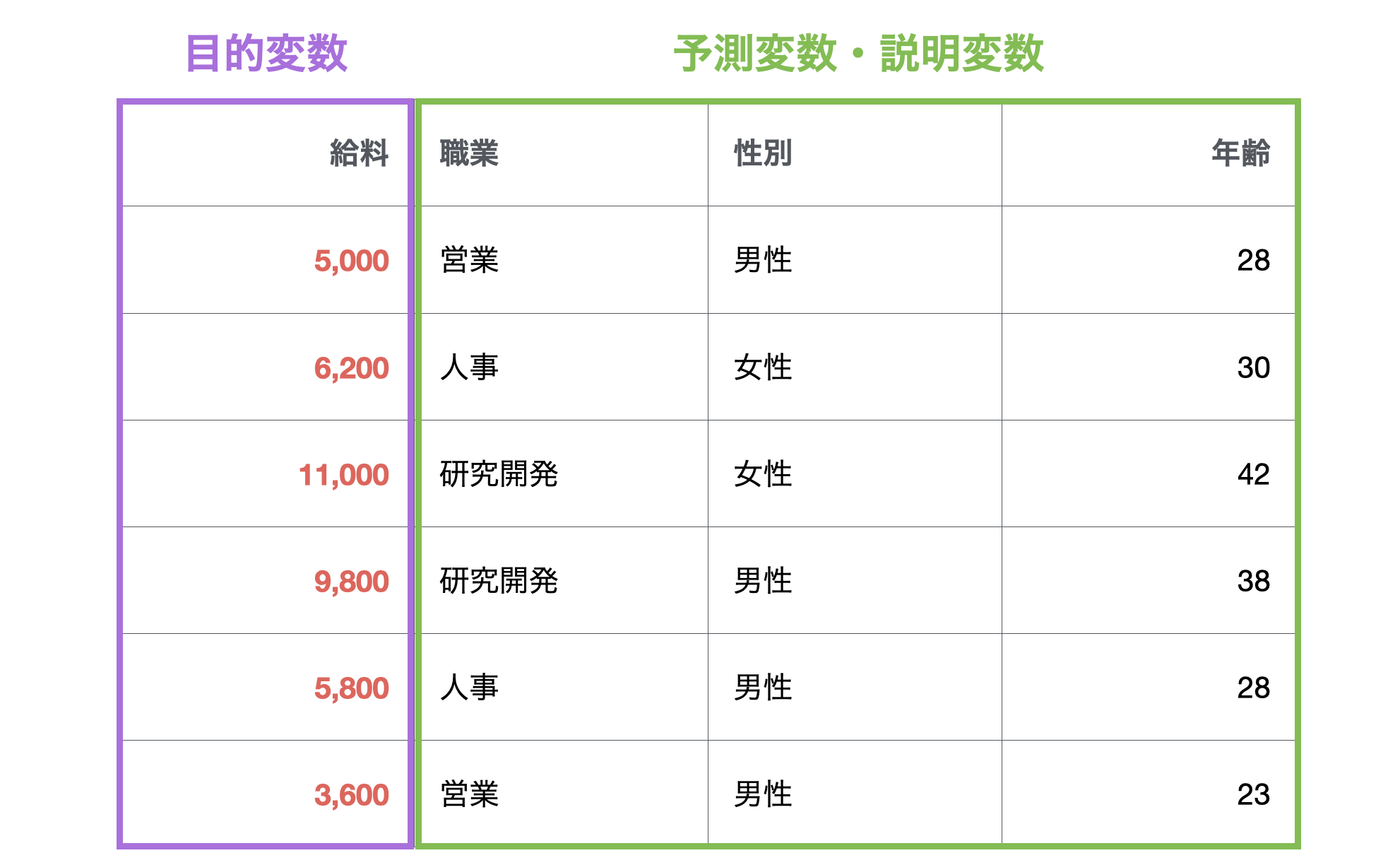
予測モデルを作る時に、予測対象の列のことを目的変数、目的変数を予測する上で使用する列のことを予測変数や説明変数と言います。
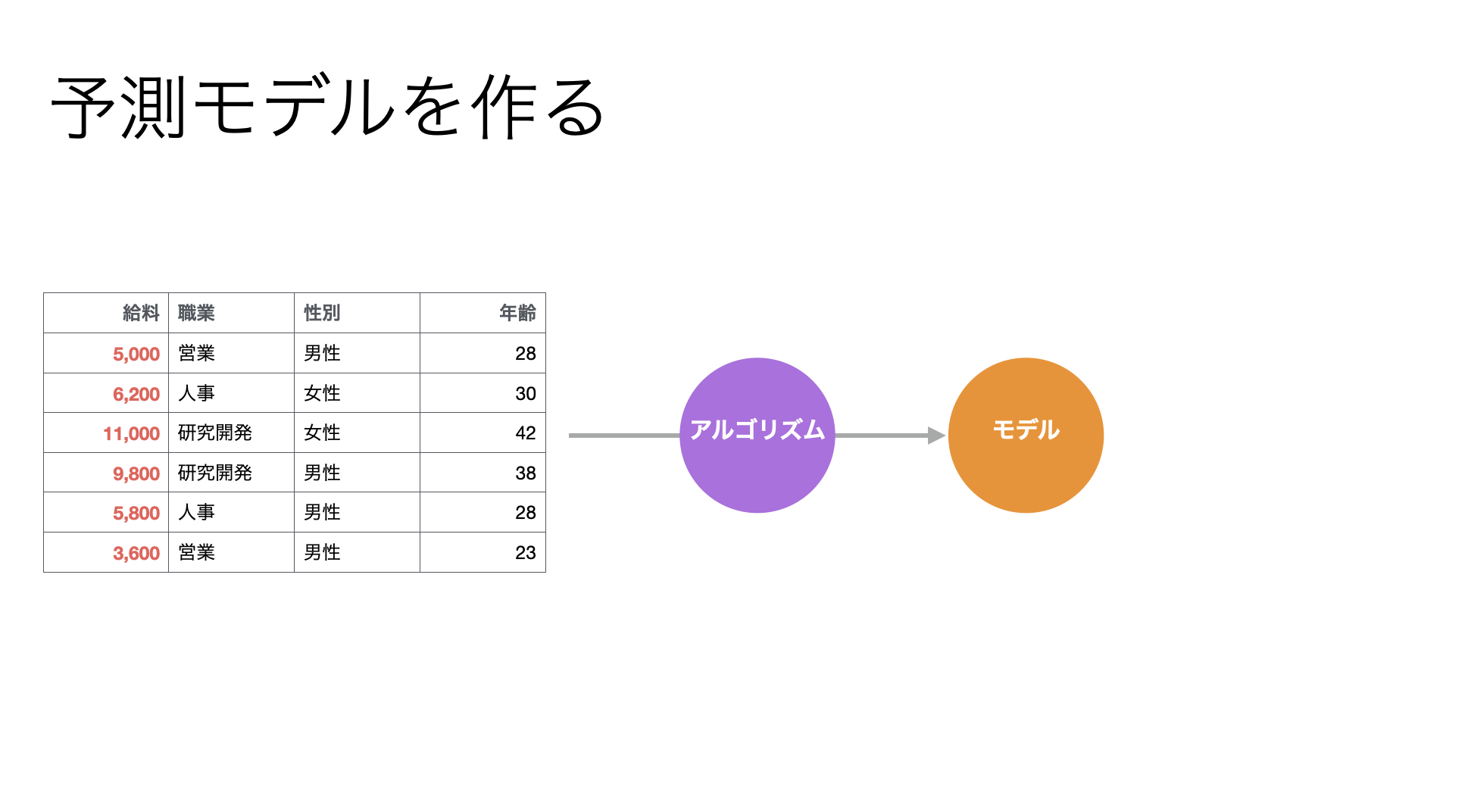
こういったデータがあれば、統計や機械学習の「アルゴリズム」を使って、顧客の属性とコンバージョンの関係をもとに、将来を予測するために、過去のデータの中にあるパターンを数式化またはルール化できます。
このように、アルゴリズムが検出したデータの中にあるパターンを表現したものを「予測モデル」と呼びます。
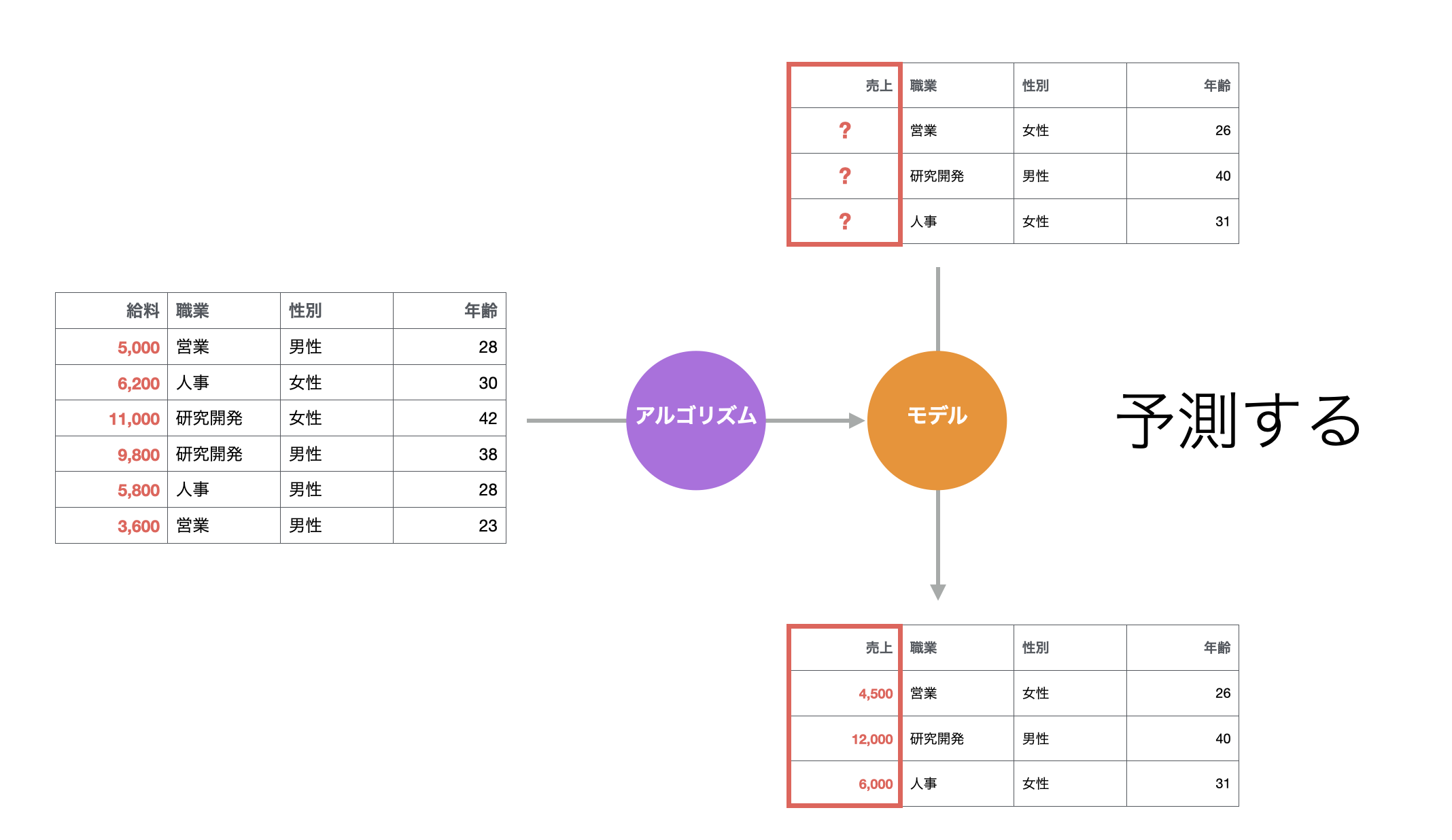予測モデルを使うと、新しい従業員が入ってくるとした時にどれくらいの給料になるのかをを予測できます。
また、予測モデルを作ると、データの中にあるパターンに関して、例えば以下のことも理解できます。
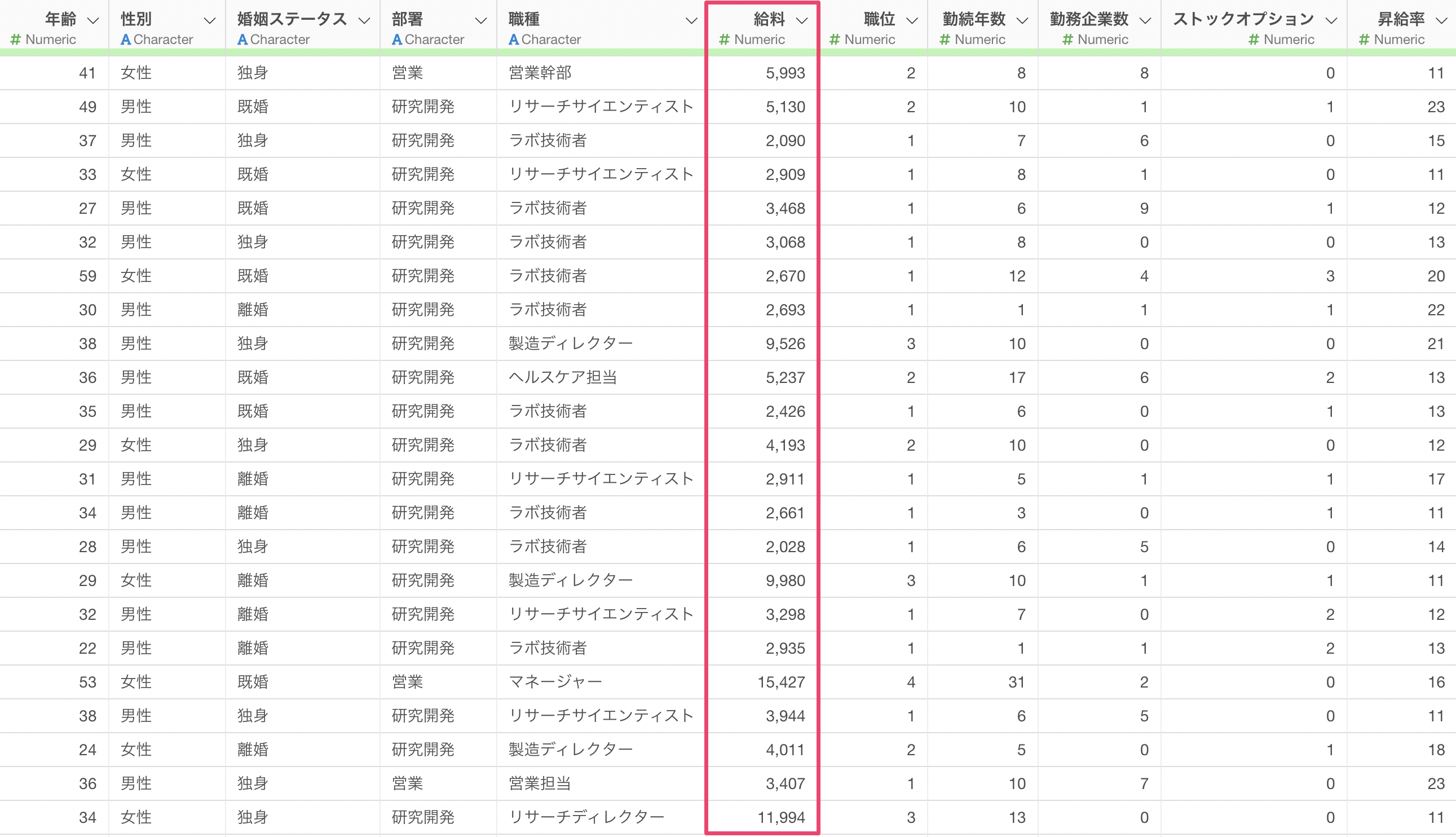
- 目的変数と関係の強い変数はどれか
- それはどういった関係なのか
- それは有意な関係なのか
- このモデルでは目的変数の動きのどれくらいを説明できるのか
5. 予測モデル：線形回帰の作成
今回は従業員の「給料」を予測する線形回帰のモデルを作成します。
アナリティクスビューに移り、タイプに「線形回帰」を、目的変数には「給料」を選択します。
説明変数をクリックして、「年齢」から「離職」までの列をシフトキーを押しながら選択します。
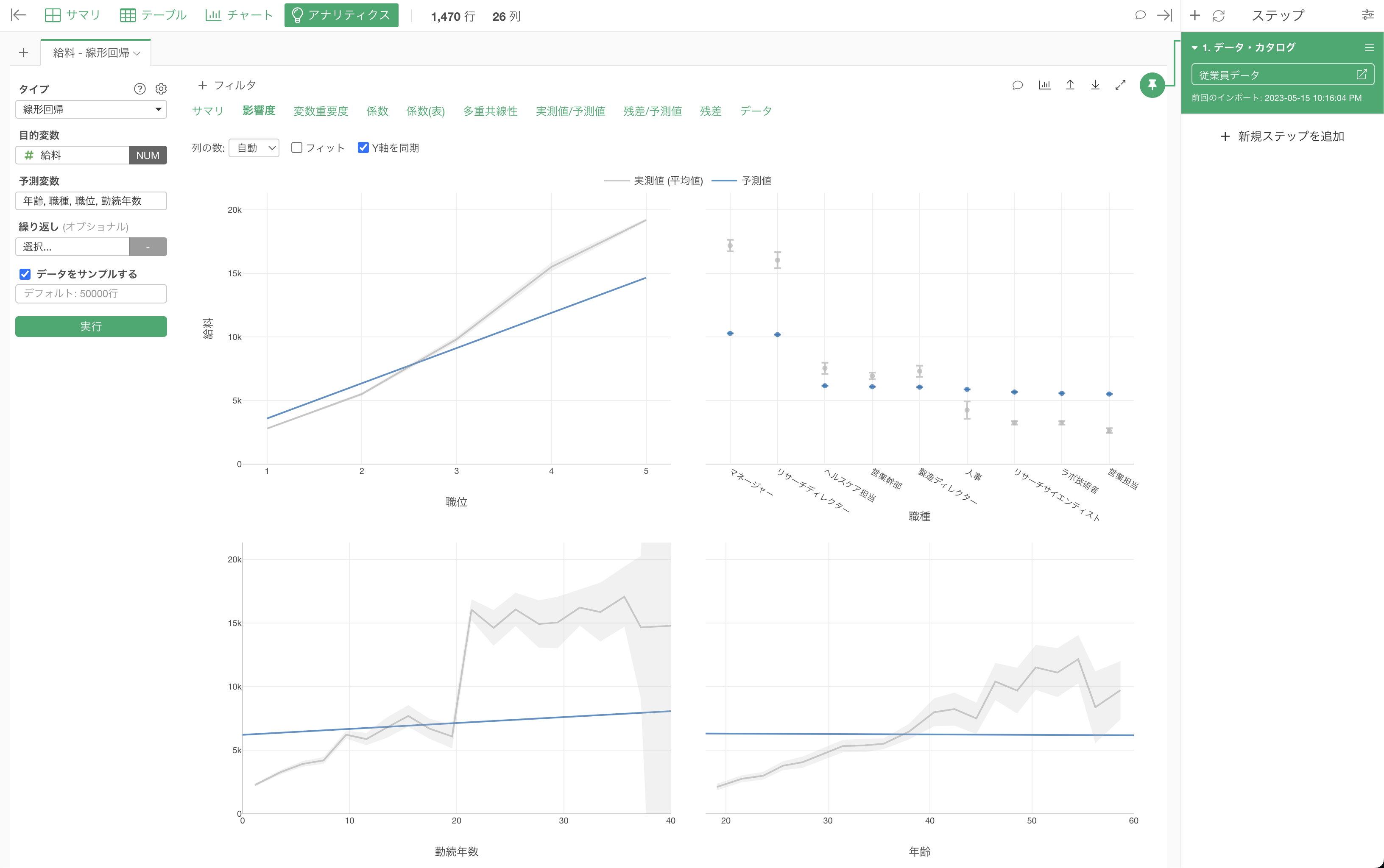
実行することで、線形回帰のモデルが作成されていることが確認できます。
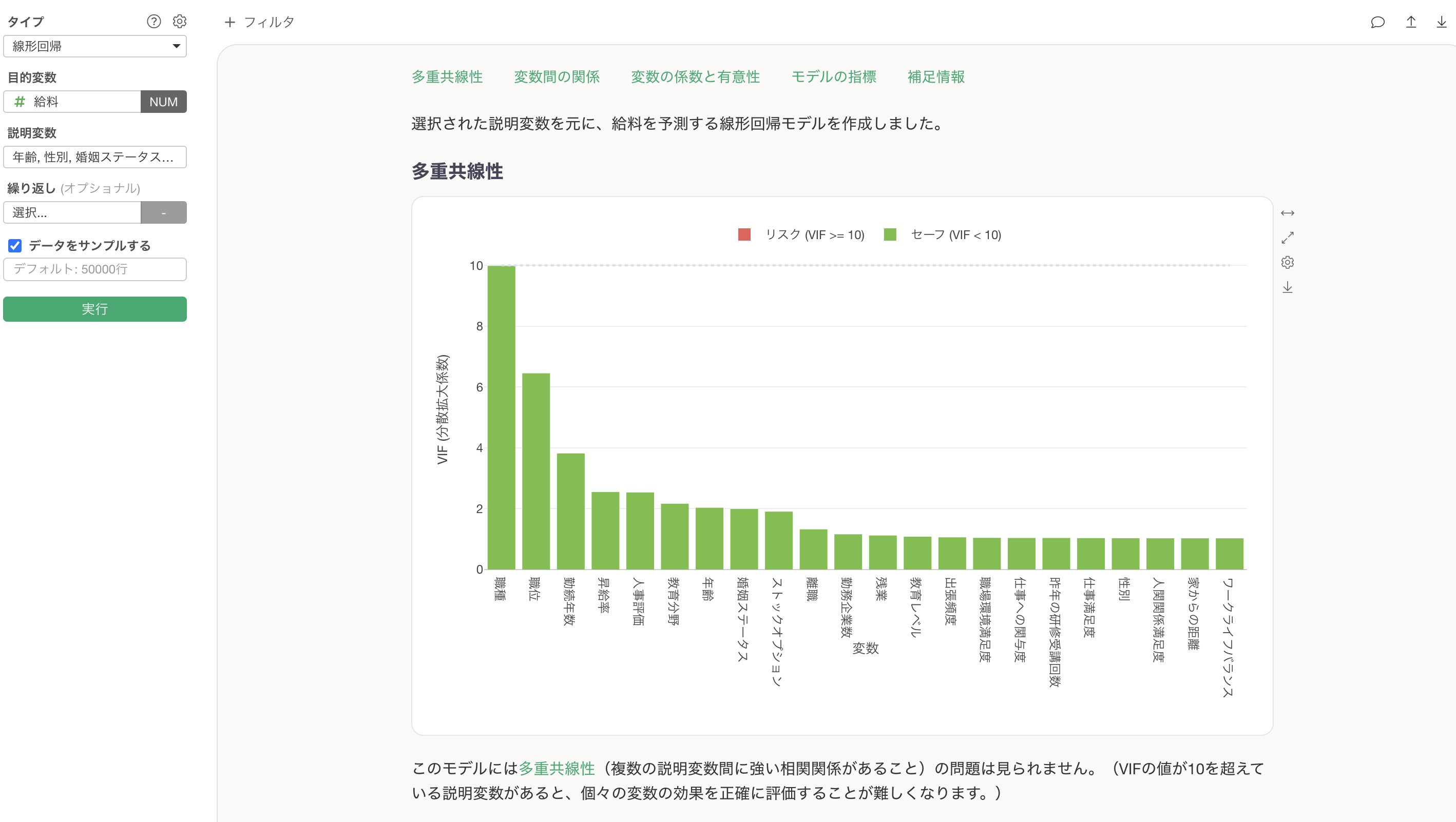
しかし、ここで1つ問題があります。それが多重共線性の問題で、線形回帰などの統計のモデルでは説明変数間に相関が強い変数があると、係数が不安定になるという問題があります。
今回の結果では多重共線性が発生（VIFが10以上）のために、「部署」か「職種」のどちらかの説明変数を取り除く必要があります。
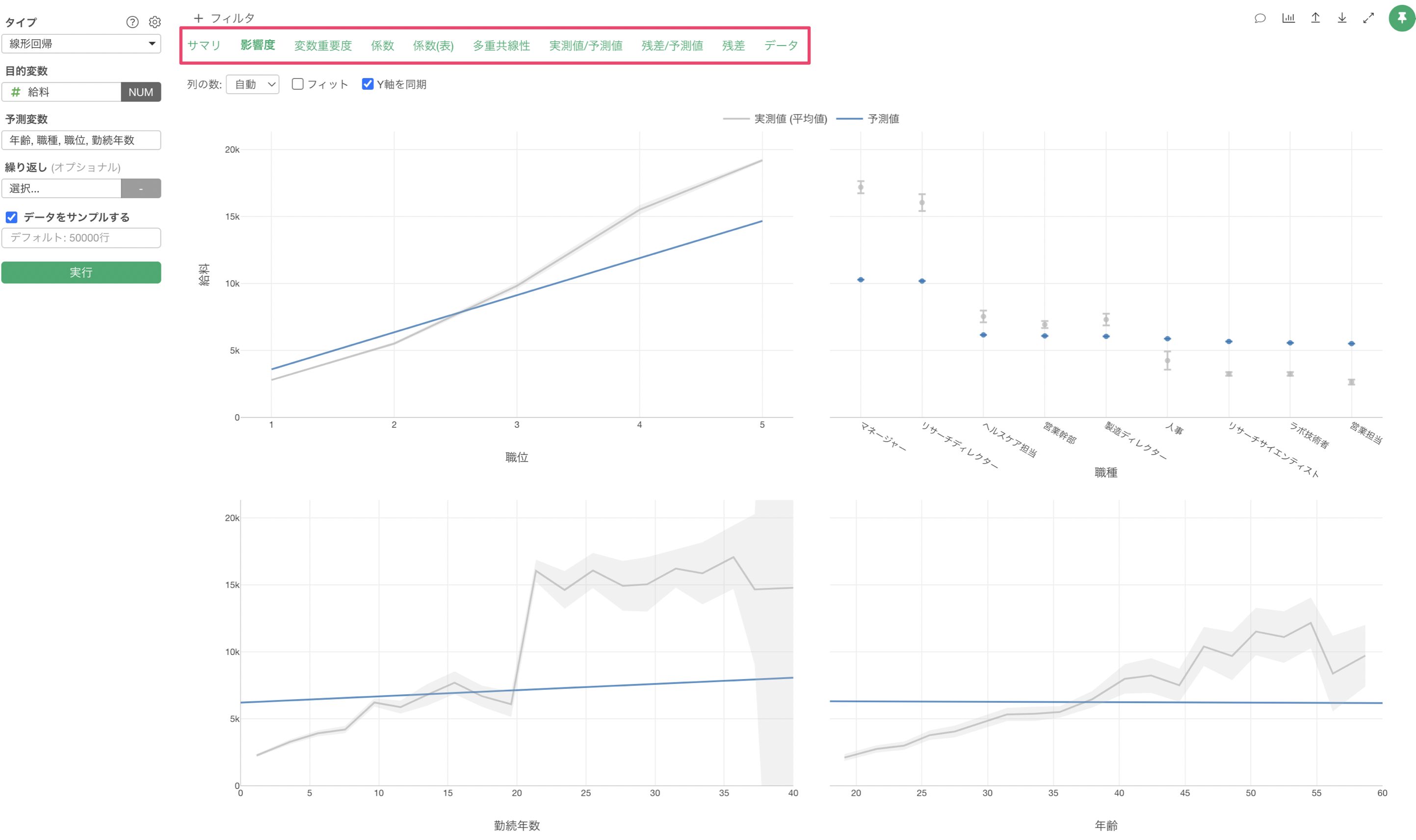
これらの分析時に留意しなければいけないものは、v13以降のバージョンではガイド付きのアナリティクスによって、分析結果を初心者でも理解できるよう、各チャートの見方や分析手法に関する詳細な説明を自動的に表示されるようになっています。
説明変数をクリックをして、部署を取り除いた上で実行をします。
これによって多重共線性の問題を解決することができました。
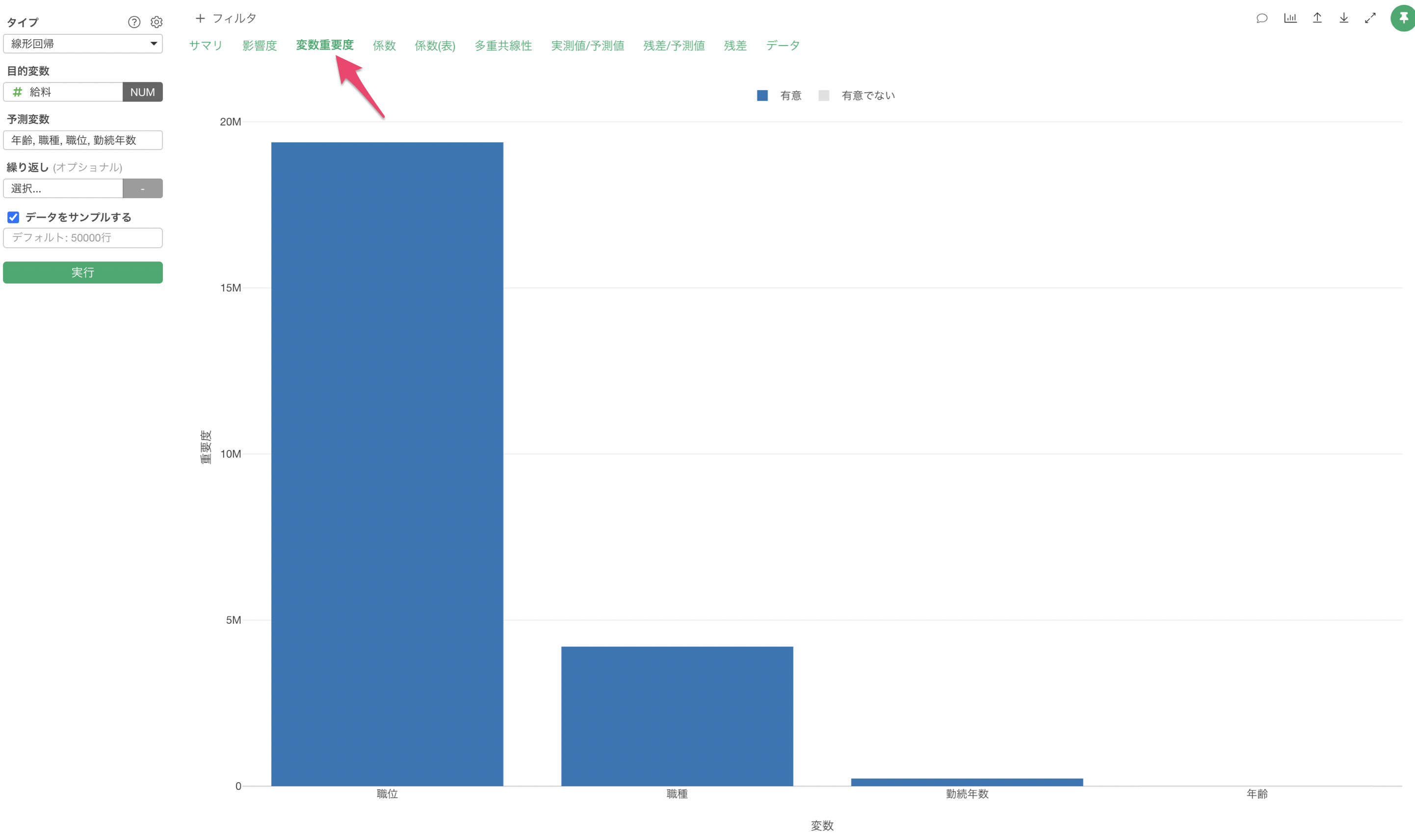
6. 予測モデルの解釈
v13のガイド付きのアナリティクスにより、アナリティクスの解釈は上から順に見ていくことで結果を理解していくことが可能です。
説明変数の重要度
説明変数の重要度のセクションでは、どの変数が目的変数とより相関が強いのか、予測する時により重要なのかを調べることができます。
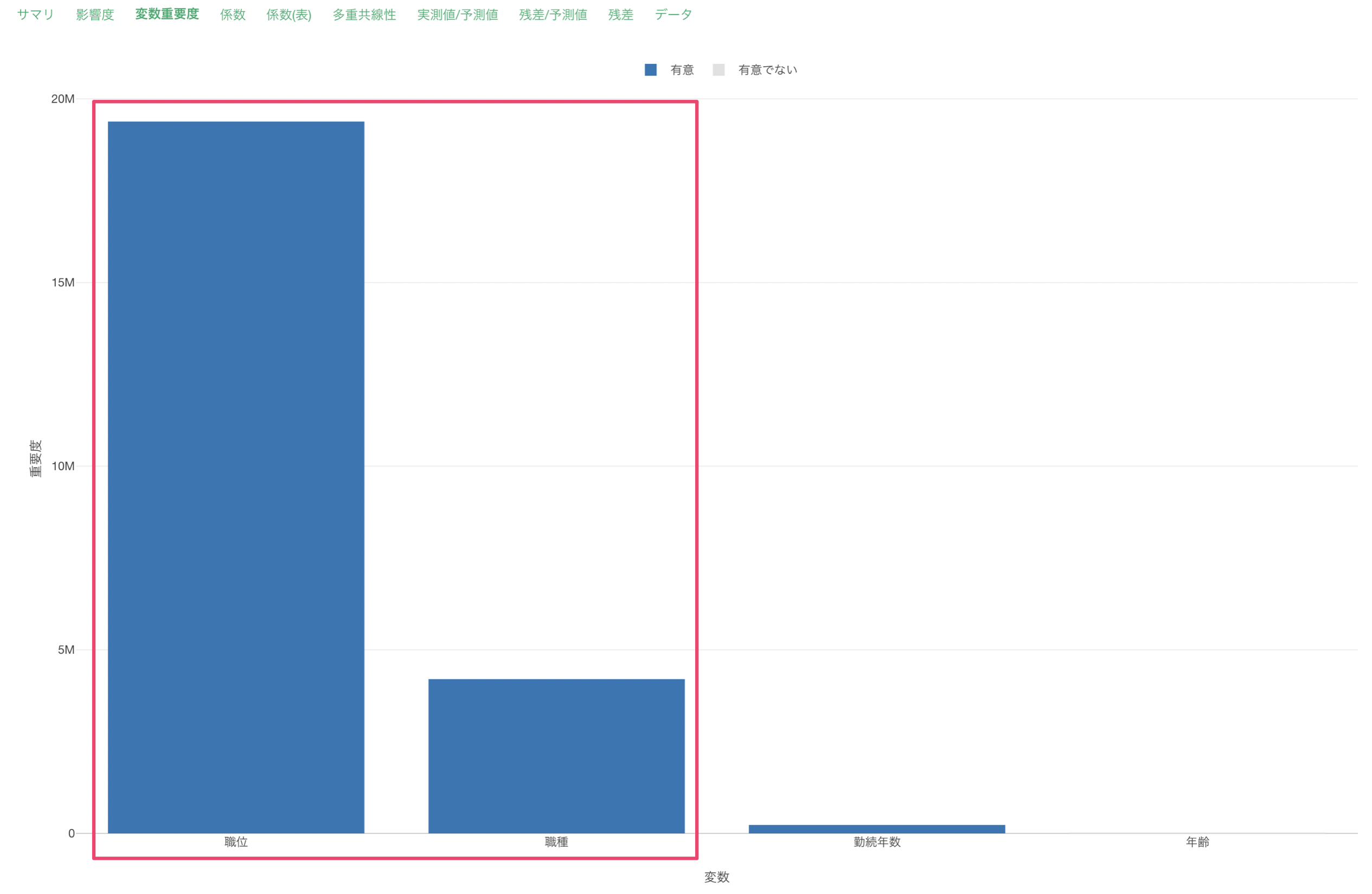
職位と職種が給料の予測に重要な変数であることがわかります。
なお、変数重要度に関する詳細は、こちらの資料をご参照ください。
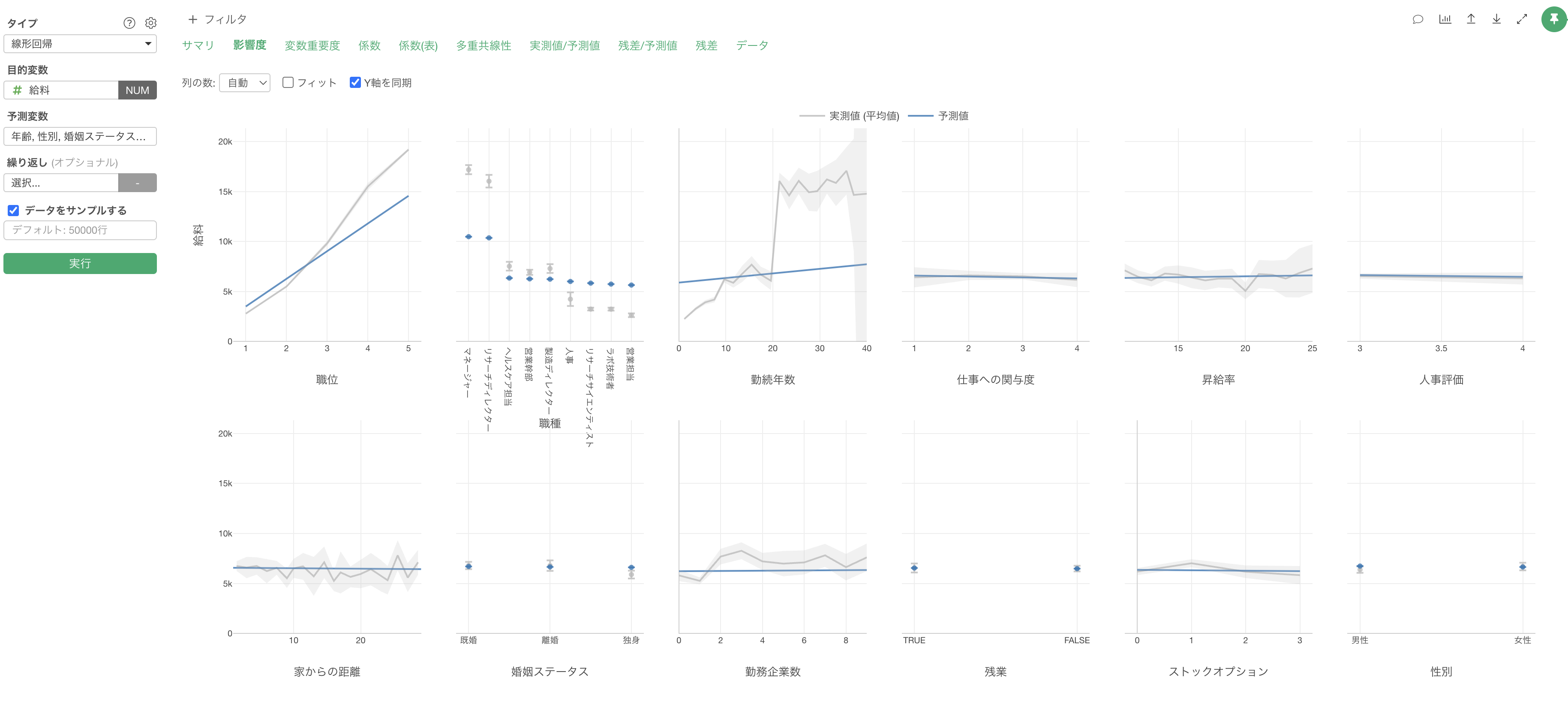
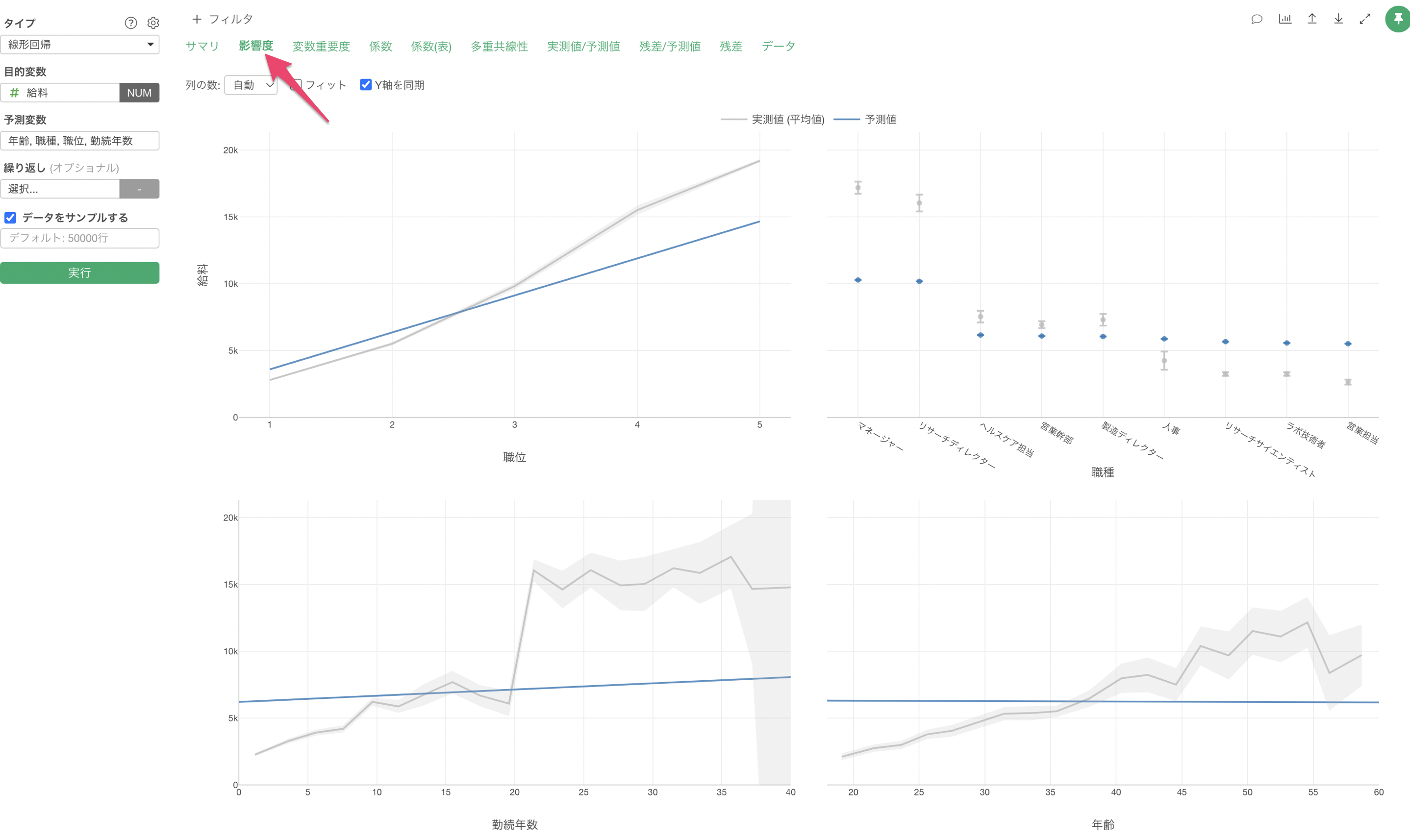
説明変数の影響度
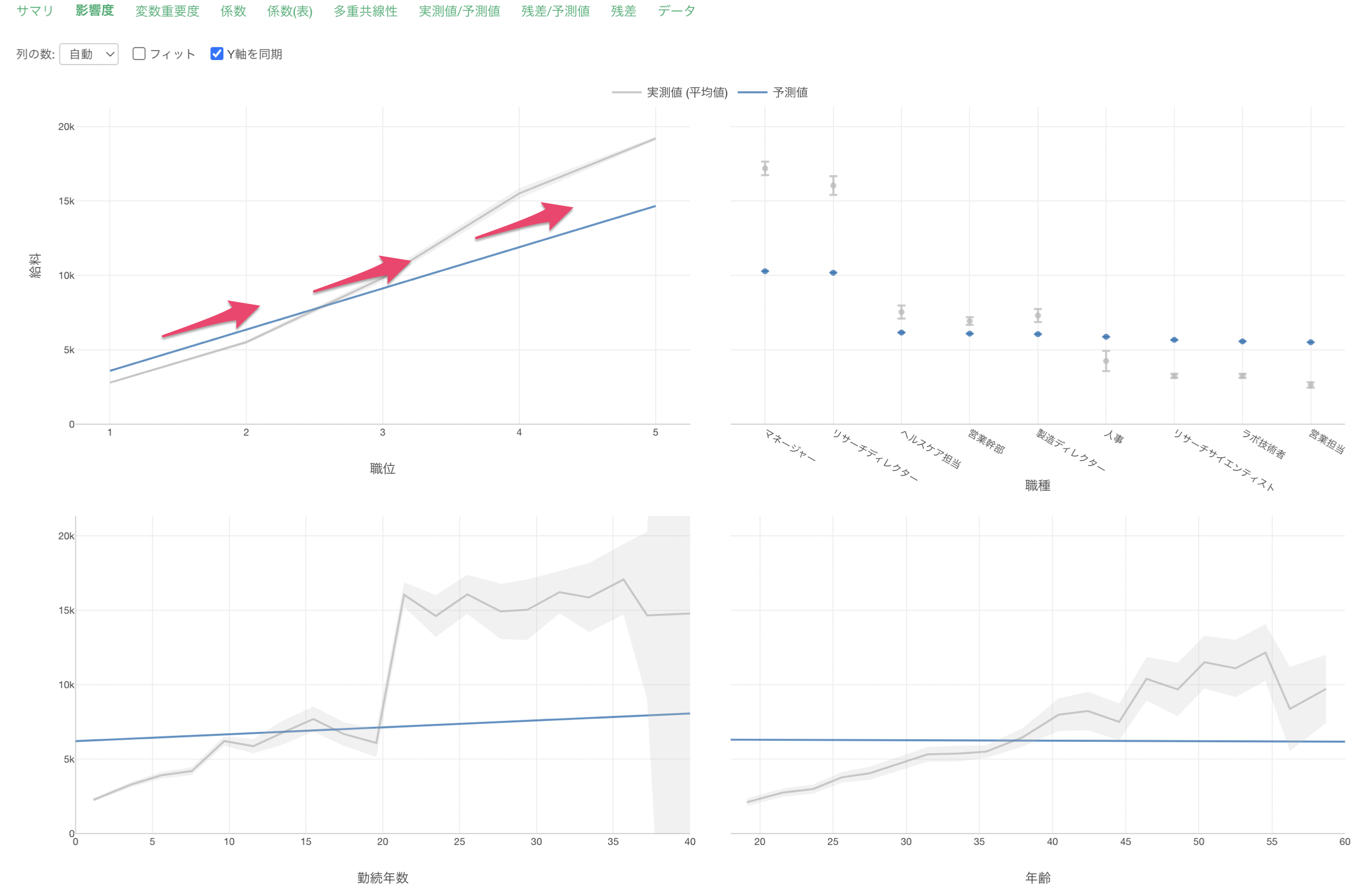
説明変数の影響度では、それぞれの変数の値が変わると、目的変数の値はどのように変わるのかがわかります。
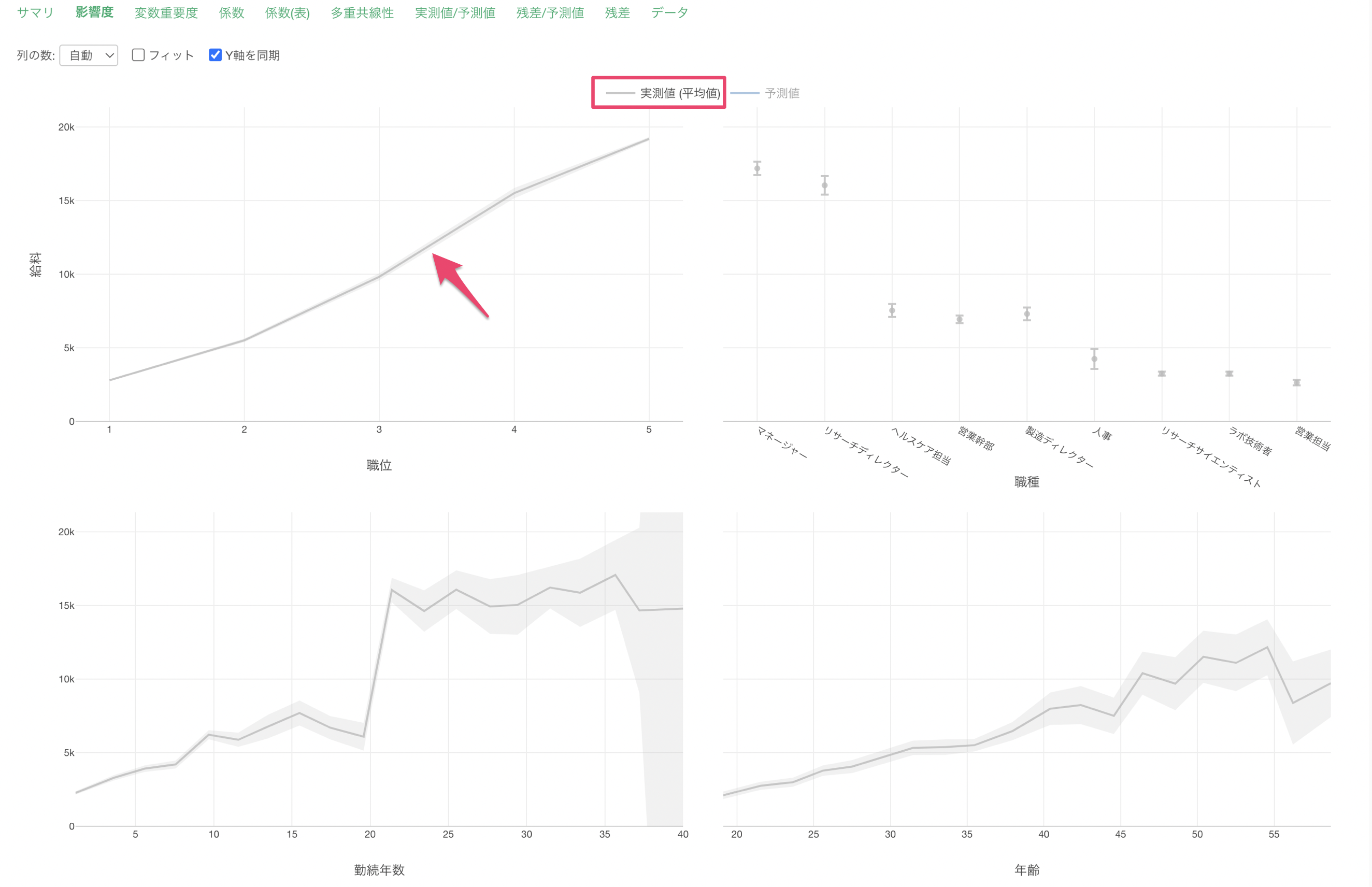
職位が上がると給料が高くなる関係があることがわかります。
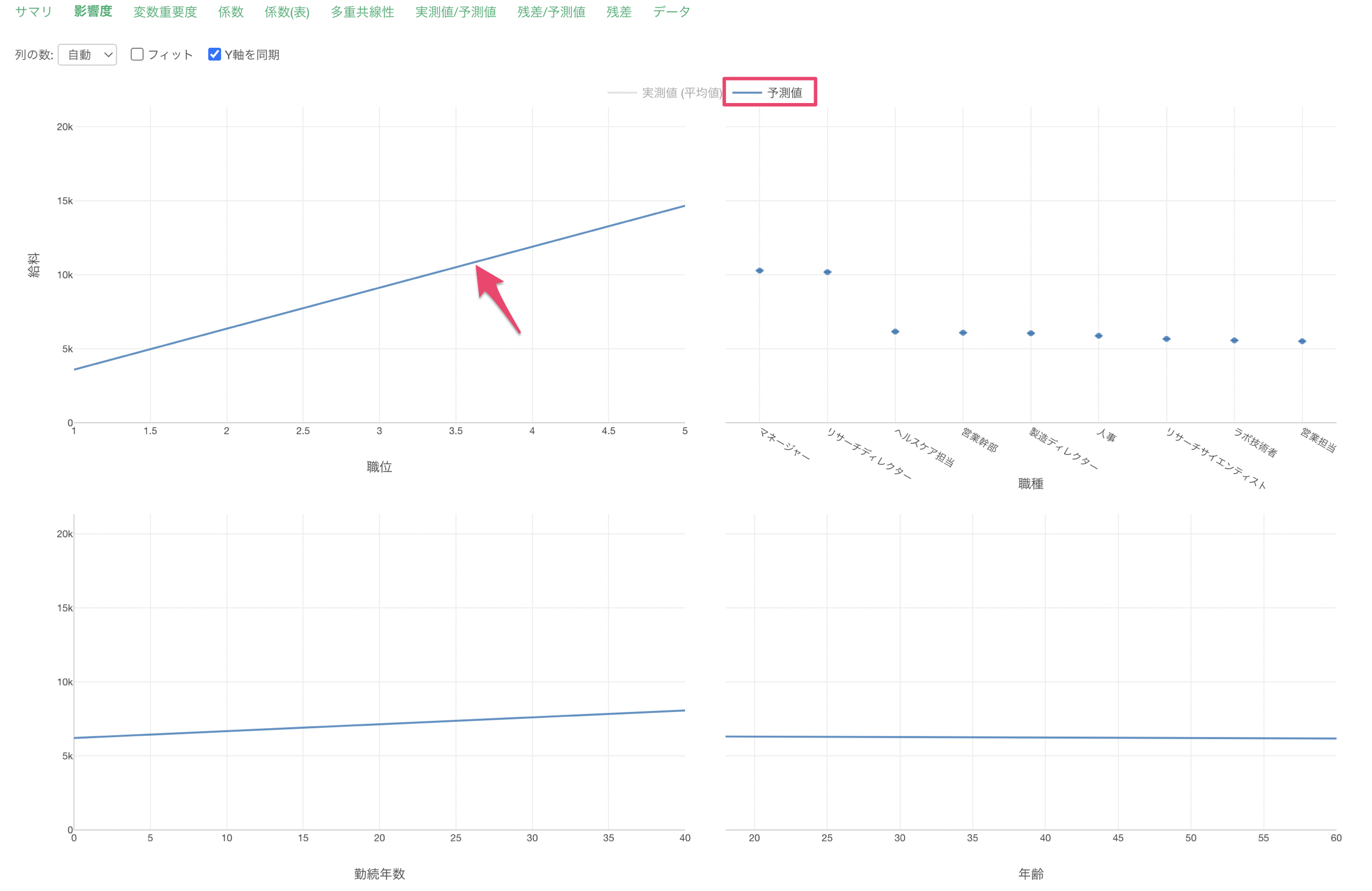
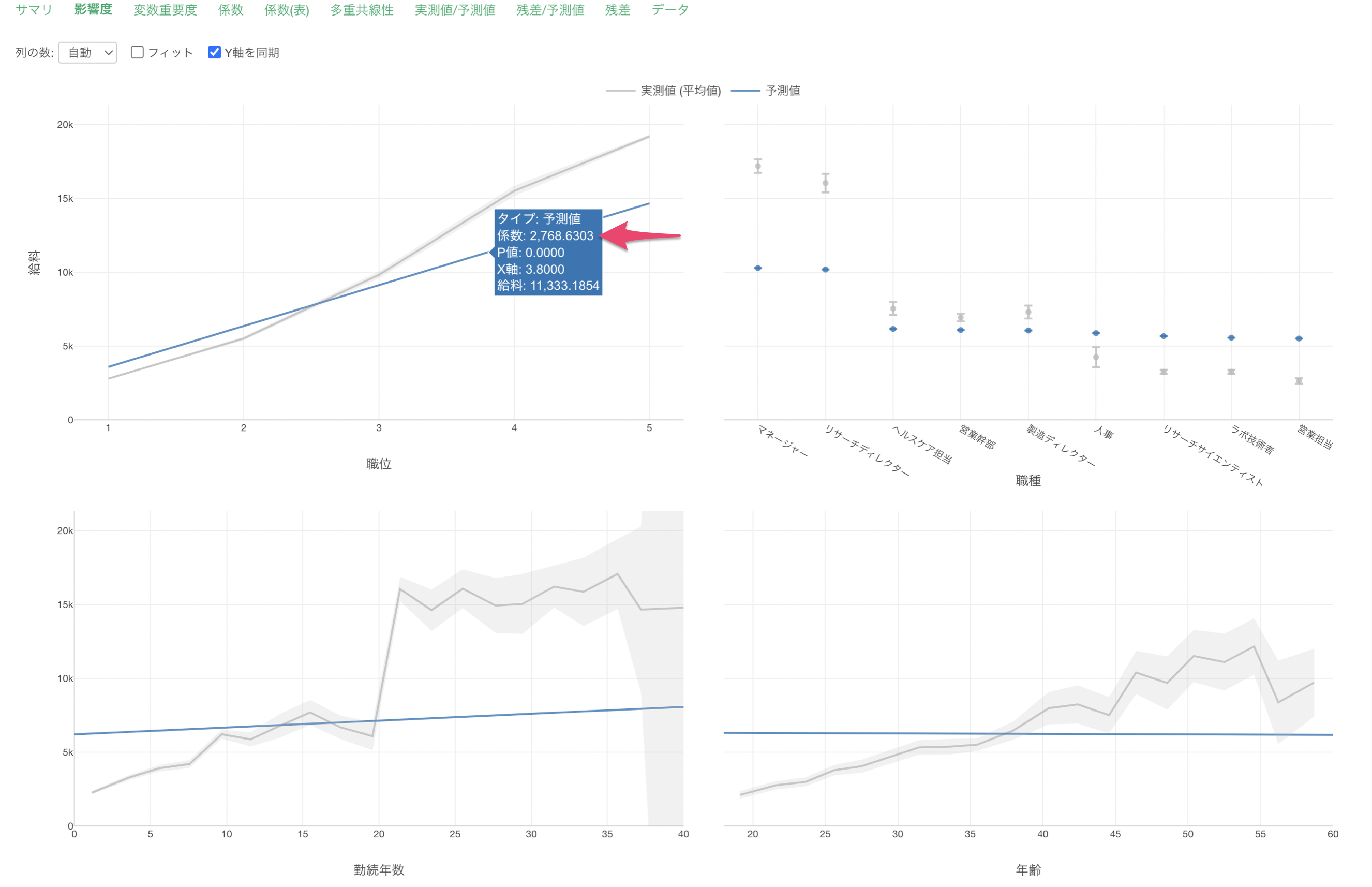
他の変数の値が変わらないと仮定した場合、職位が1上がると給料が2,766ドル（係数）上がるということがわかります。
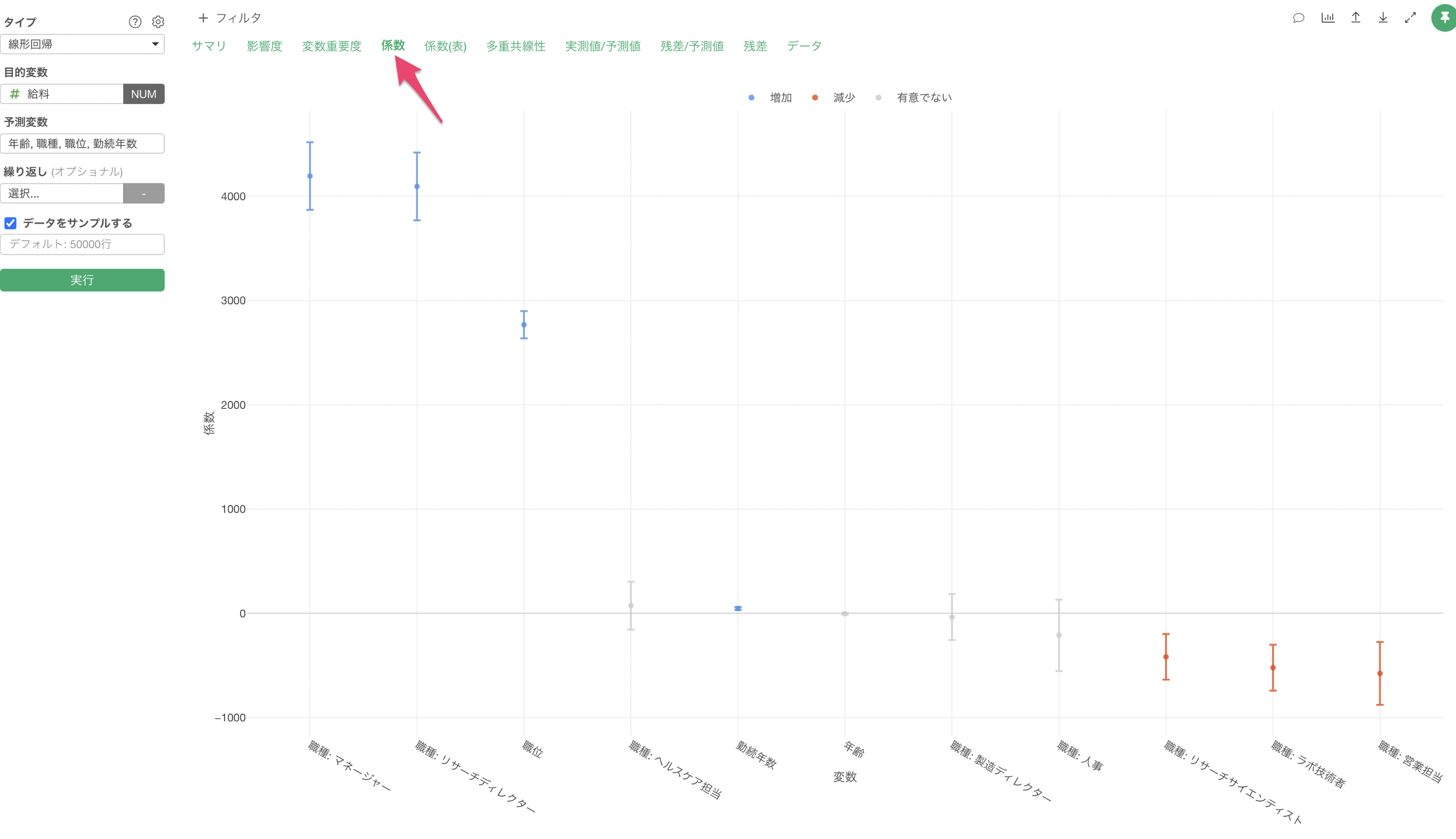
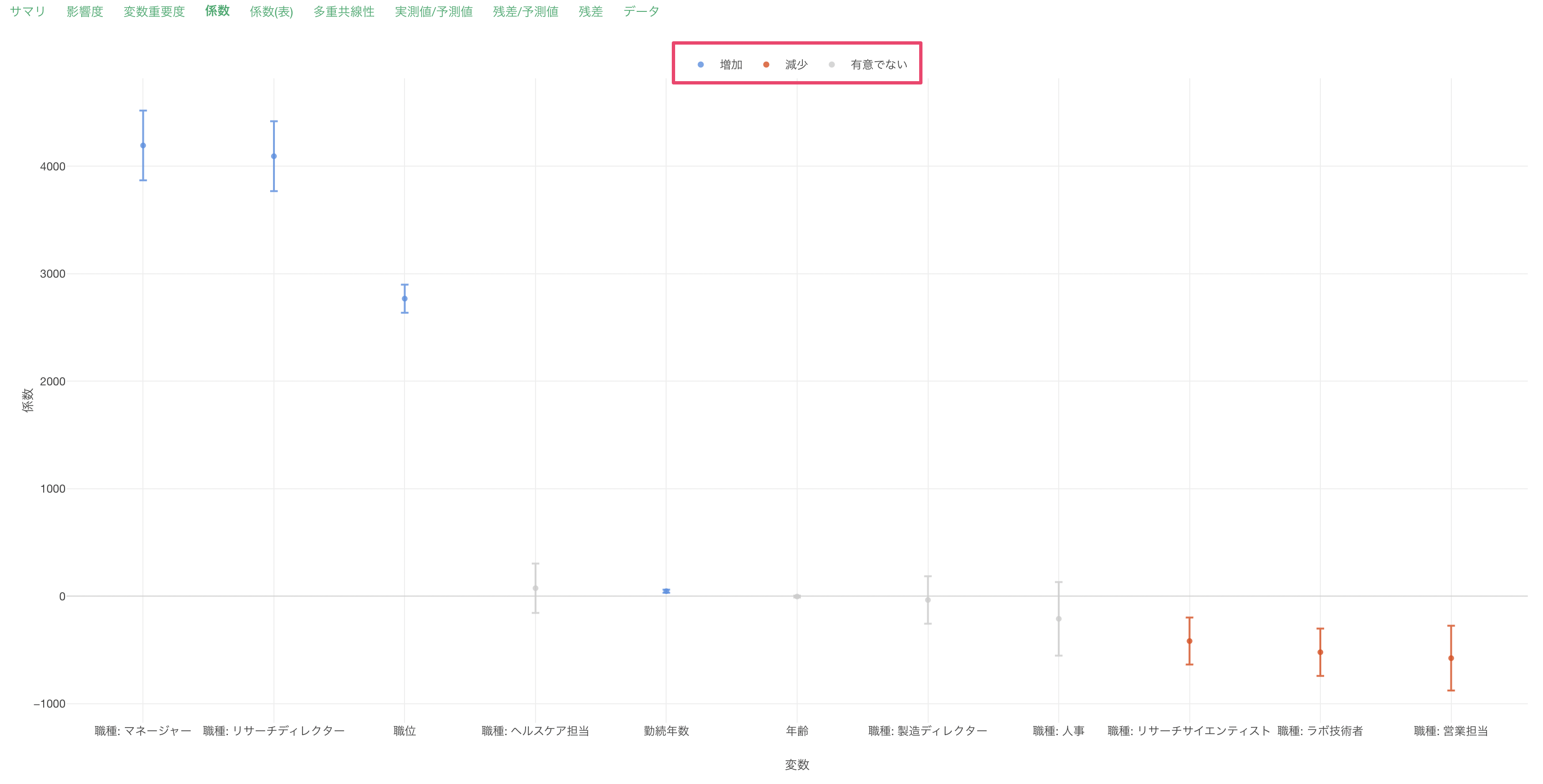
係数と信頼区間の可視化
「係数と信頼区間の可視化」では、それぞれの変数の値が1単位変わったときに変化する給料の値とその信頼区間が可視化されています。
それぞれのエラーバーは、給料が増加する場合は青、減少する場合は赤、さらに増加するとも減少するとも言えない場合はグレーで表示されています。
モデルの指標
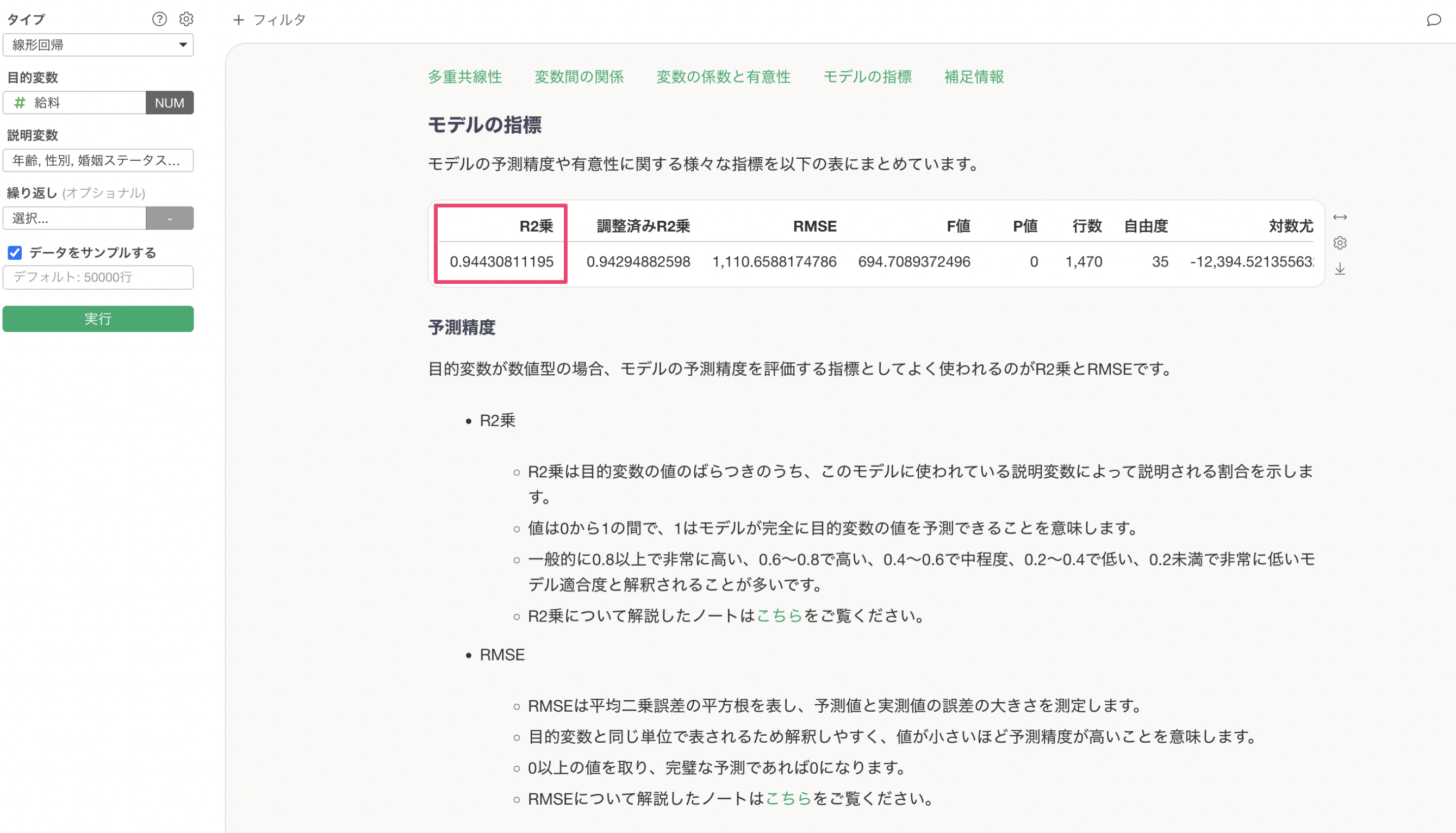
モデルの指標では、この予測モデルの予測精度などが確認できます。
R2乗はデータの平均からのばらつきをモデルが説明できている割合の指標で、0から1の間の値を取ります。1に近ければ近いほど、モデルがデータのばらつきをよく説明できていることを示します。
今回作成したモデルのR2乗は0.943なので、このモデルは給料のばらつきの94.3%を説明できていると解釈できます。
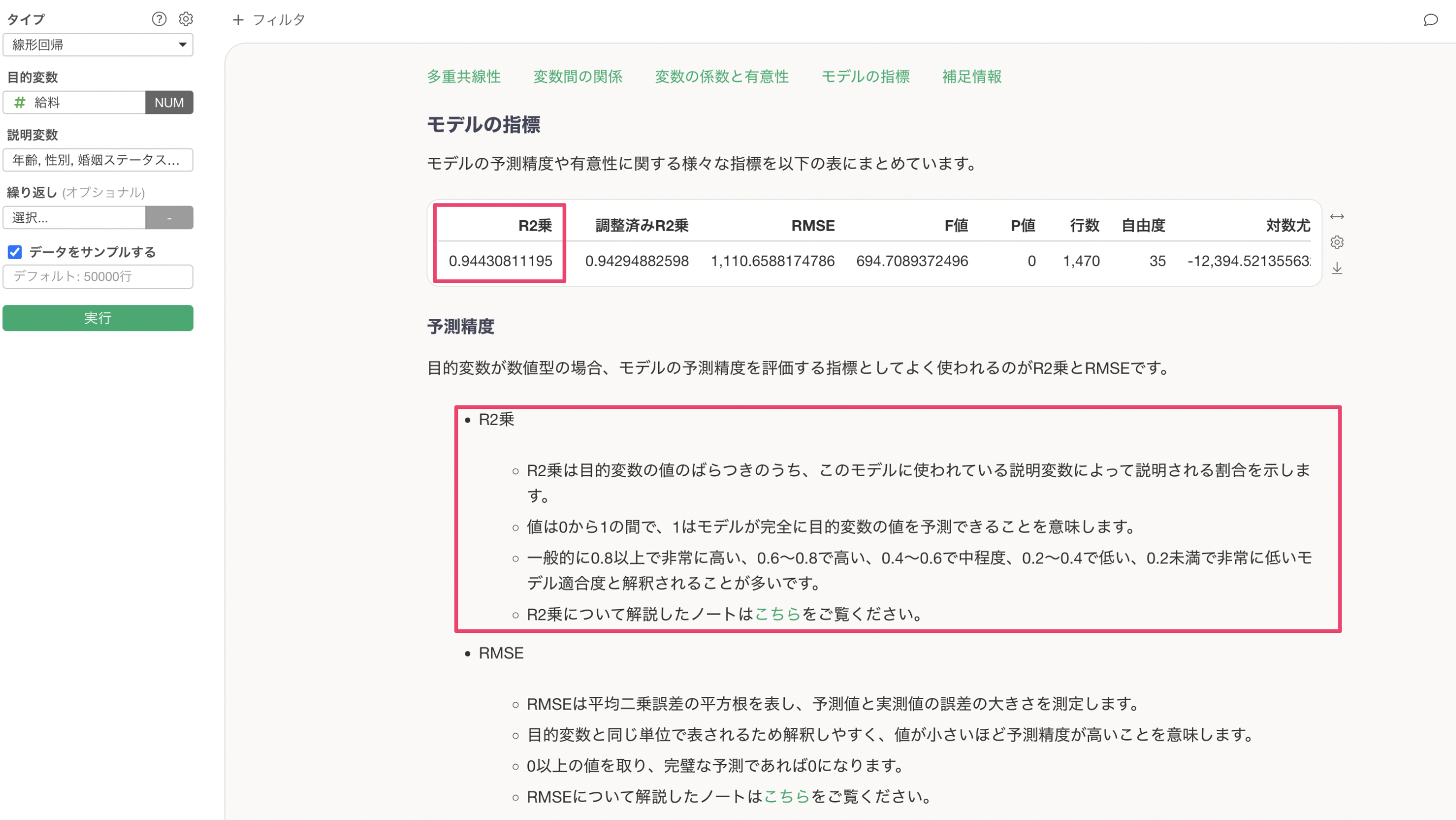
予測精度の下には、R2乗やRMSEの指標の解釈方法について解説しています。
さらには、「その他の指標の説明」のプラスボタンをクリックすることで、全ての指標について解説がされるようになっています。
線形回帰の詳細については、こちらのセミナーでも紹介しておりますので、興味がある方はご覧ください。
7. テキスト分析
今回使用するのは「顧客満足度調査」のデータです。
このデータには、お客様からの「推奨度の理由」のコメントが含まれています。
こういった自由記述の回答は、回答者が少ない場合は1つ1つ読んでいけますが、多い時には全体像がつかみにくいといった問題があります。
そこで、Exploratoryでは「テキスト分析 - 単語のカウント」を実行することで、文章を「単語」に分けて、それぞれの単語の出現頻度、一緒に使われている単語の傾向を把握することが可能です。
テキスト分析を実施したいため、アナリティクス・ビューを開きます。
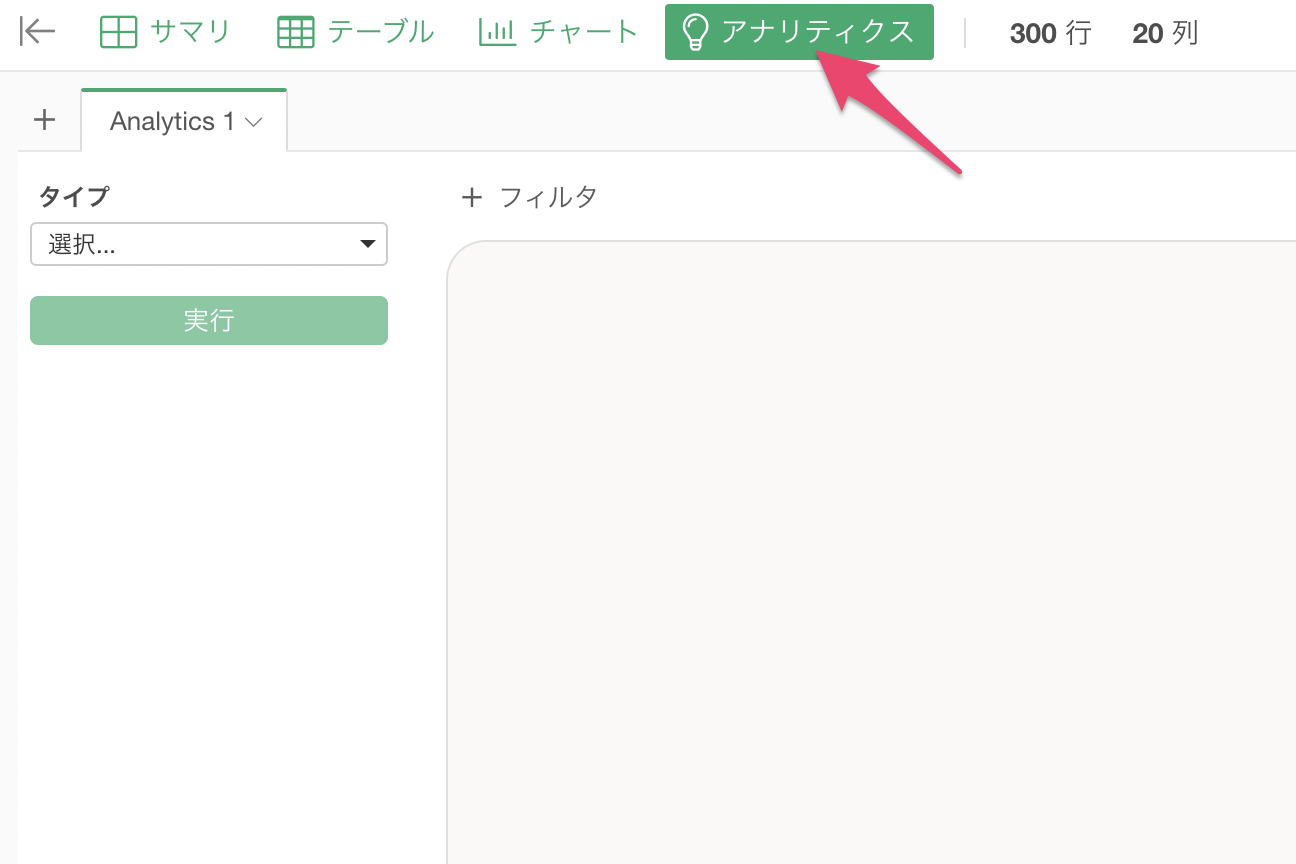
アナリティクスのタイプに「テキスト分析」→「単語のカウント」を選択します。
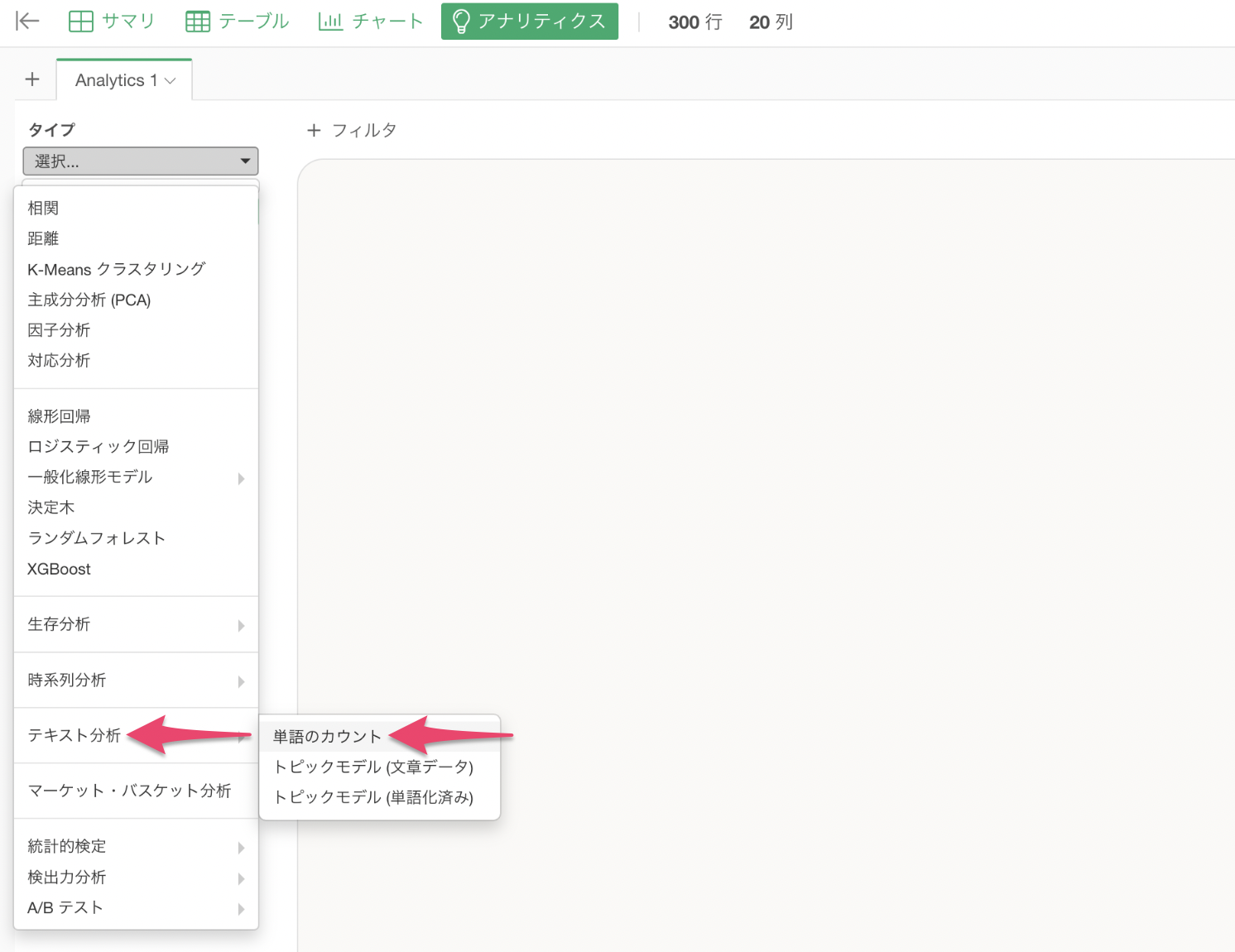
テキストの列に「推奨理由コメント」を指定して実行ボタンをクリックします。
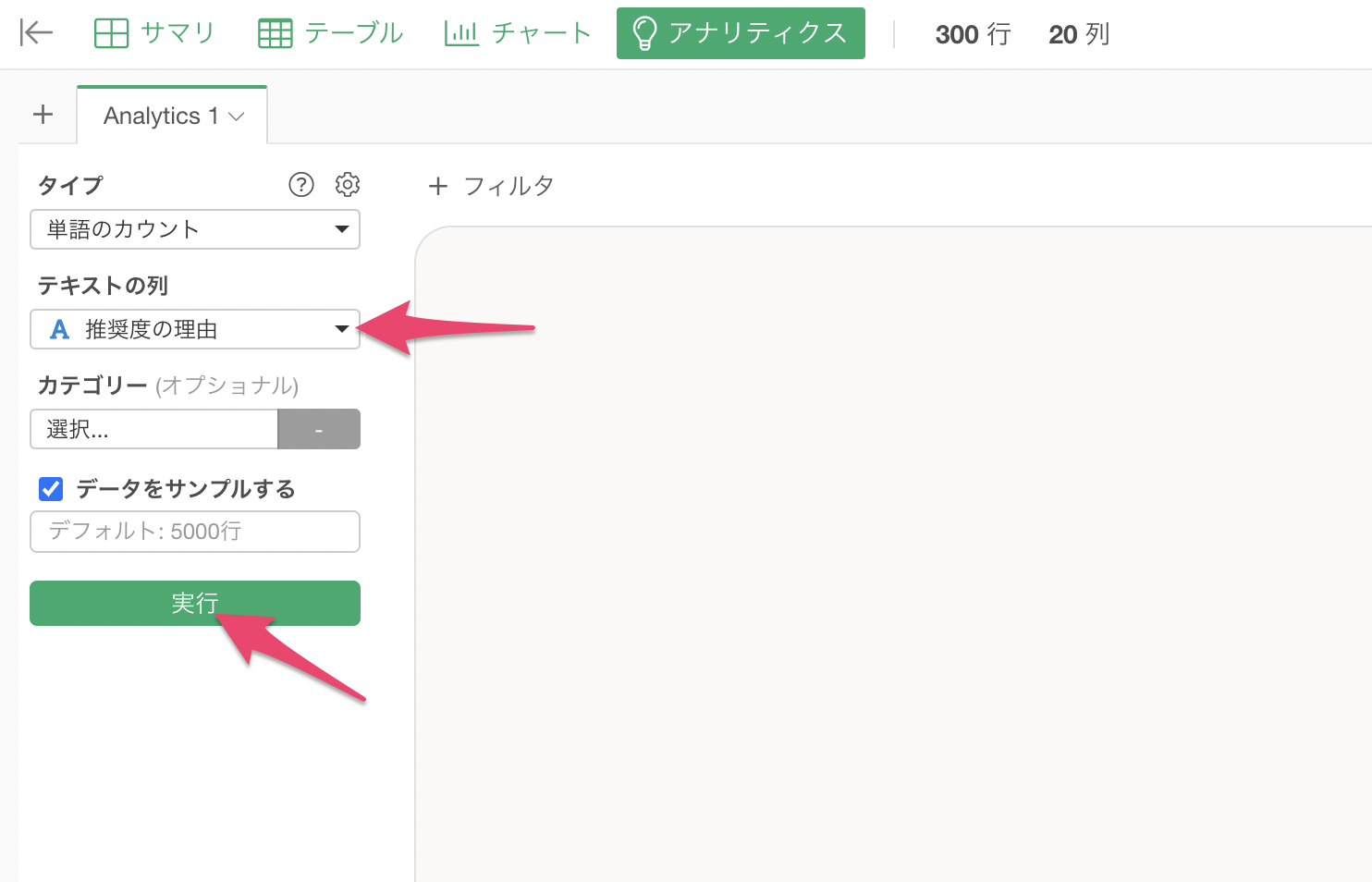
単語のカウント分析が実行され、アナリティクスガイドにより、各セクションで詳細な説明が表示されます。
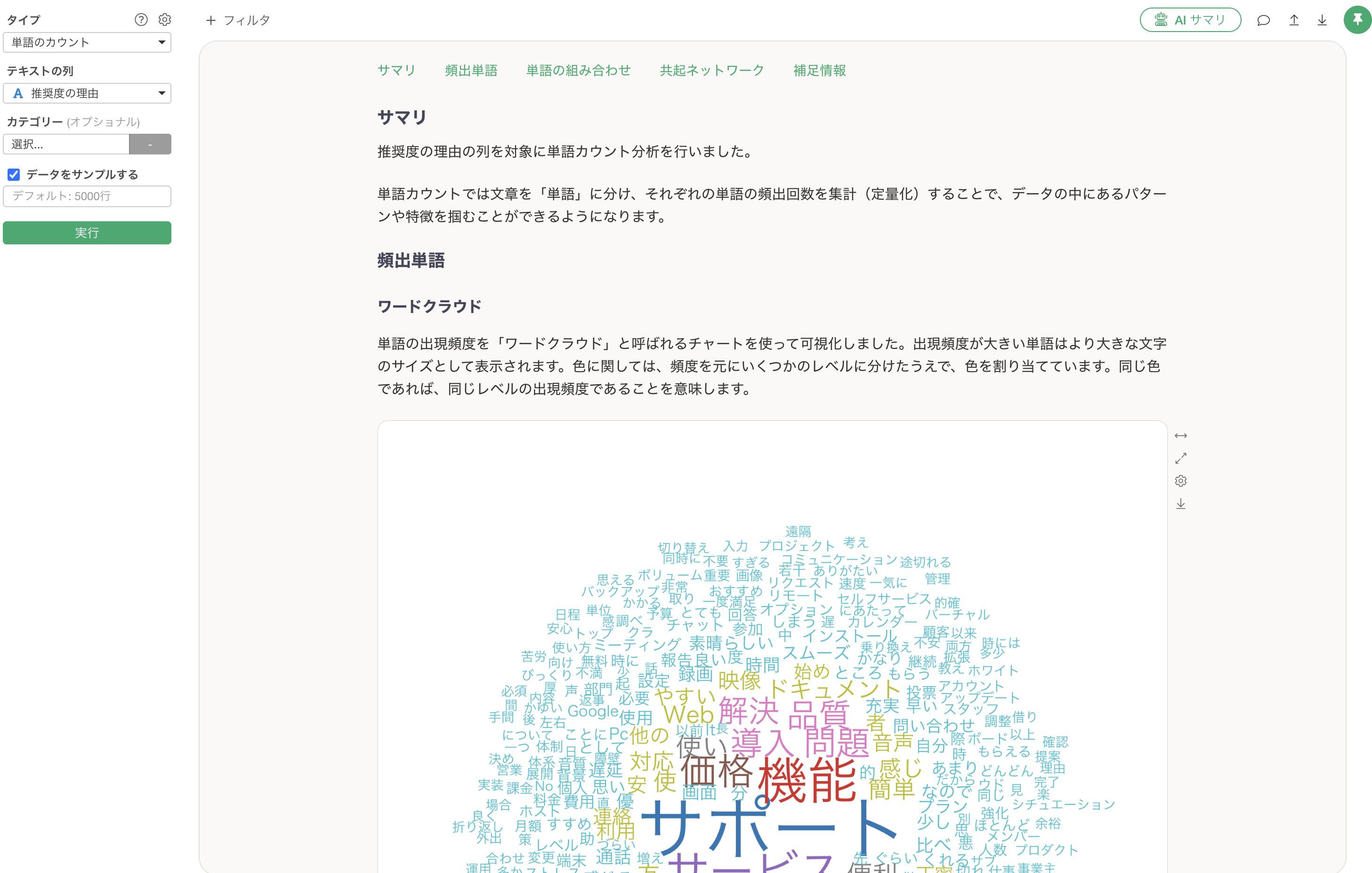
頻出単語
ワードクラウドは、テキスト全体の傾向を一目で把握できる機能です。重要な単語ほど大きく表示されるため、経営陣への報告やチーム内での情報共有の際に「今回の調査で何が最も重要だったか」を瞬時に伝えることができます。
単語の組み合わせ
単語の組み合わせでは、単独の単語では見えない「一緒に使われる単語の傾向」を発見できます。
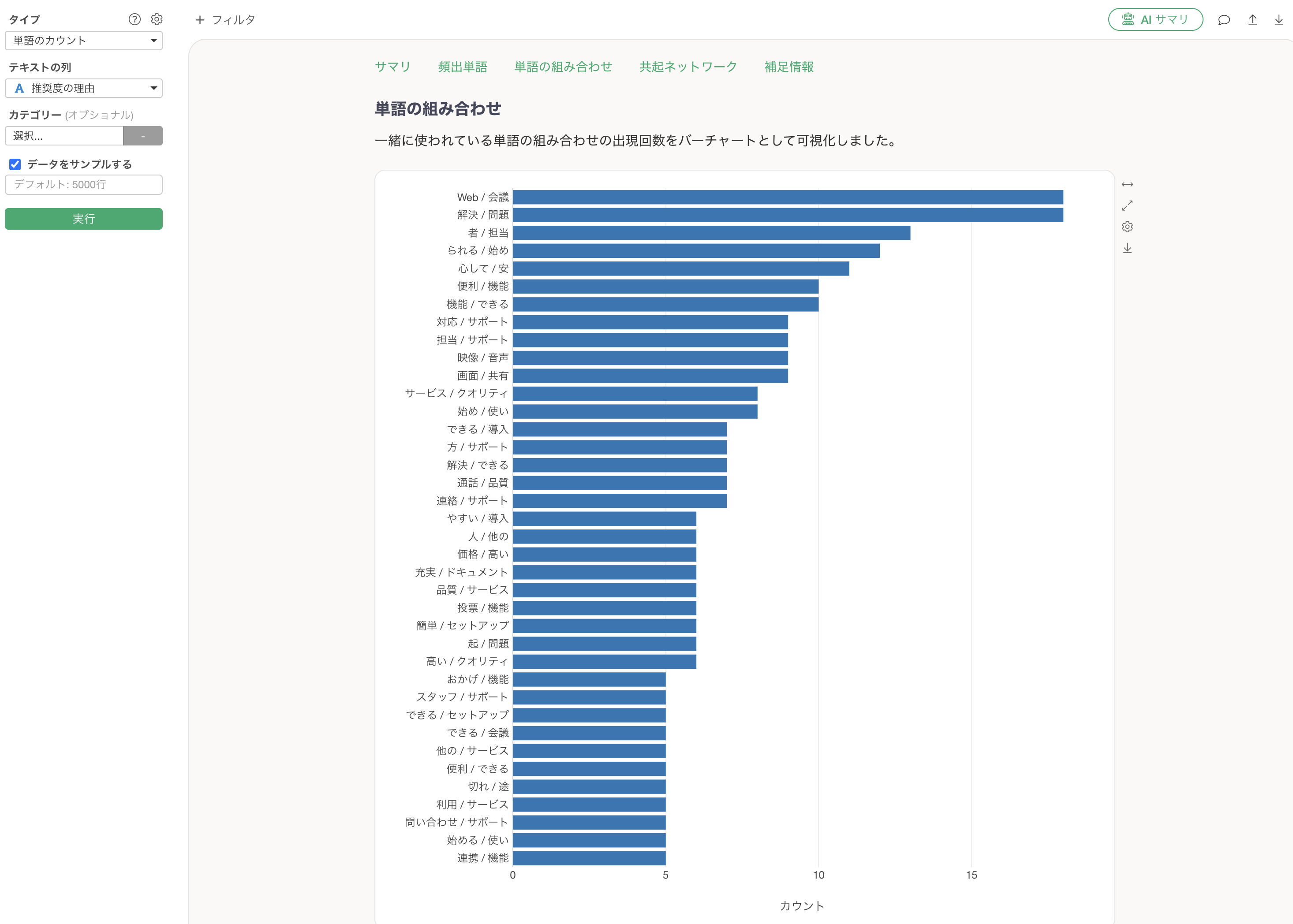
共起ネットワーク
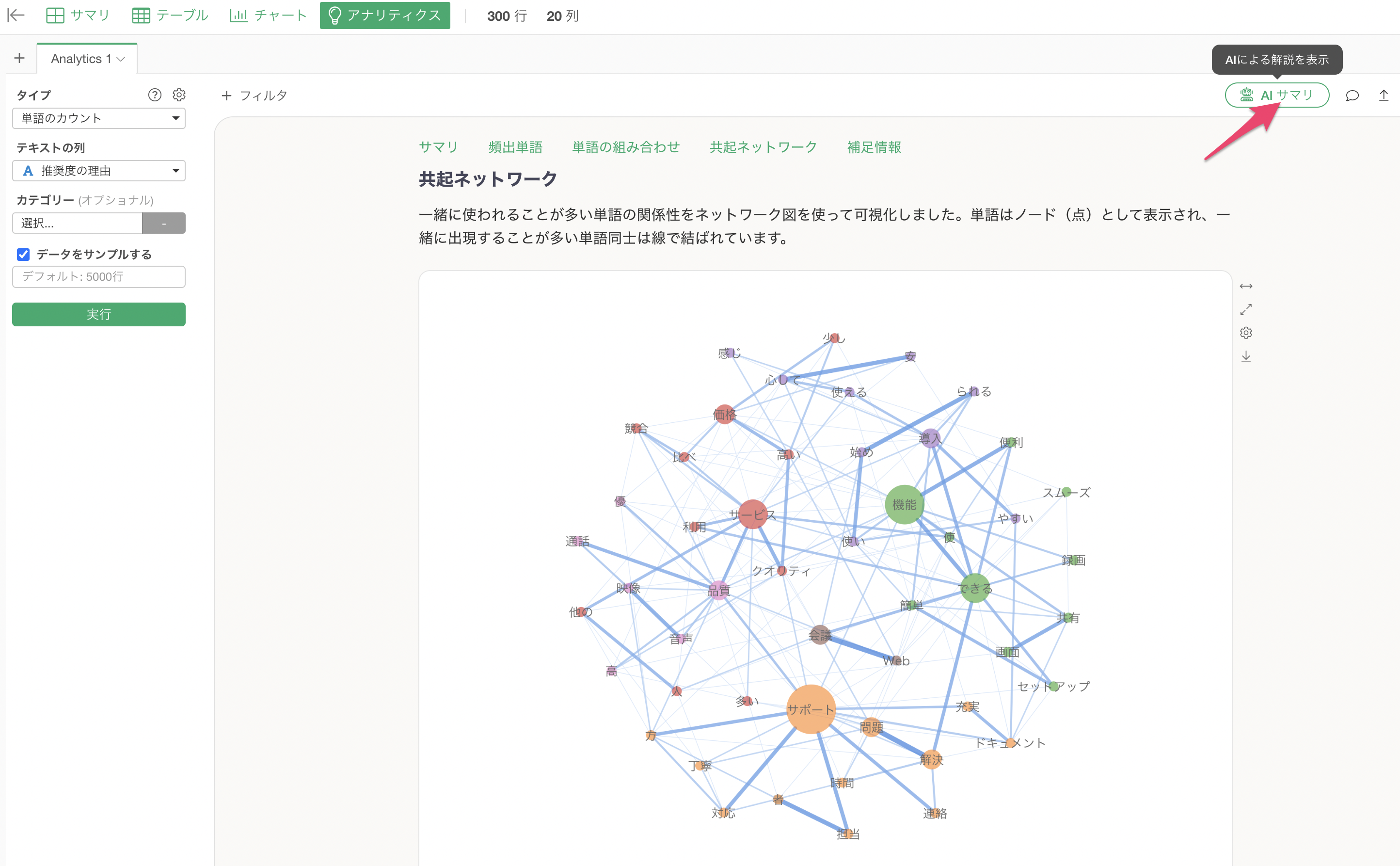
共起ネットワークは、一緒に使われている単語をグループに分け、その関係性を可視化したチャートです。これにより、どういったグループ、そして言葉が使われているのかを俯瞰して確認していくことができます。
この共起ネットワークにおけるチャートの見方は、アナリティクスガイドによって解説してくれています。
しかし、この共起ネットワークでは、どういった単語グループがあるのかはわかりますが、以下のような問題があります。
- グループを自分で識別しなければいけないために、見るのに時間がかかる。
- 実際にはどういった文脈でその単語が使われていたのかがわからない。
そこで、次に紹介する「AI サマリ」の機能を使うことで、これらの問題を解決することができます！
AI サマリを使って分析結果を要約
「AI サマリ」機能では、分析結果を自動的に要約してくれます。
単語のカウントの分析の実行画面の右上にある「AI サマリ」のボタンをクリックします。
これによってテキスト全体の傾向を要約した「サマリ」の情報と、各グループの特徴と実際の文章をまとめた「頻出単語のグループ分け」の情報が出力されます。
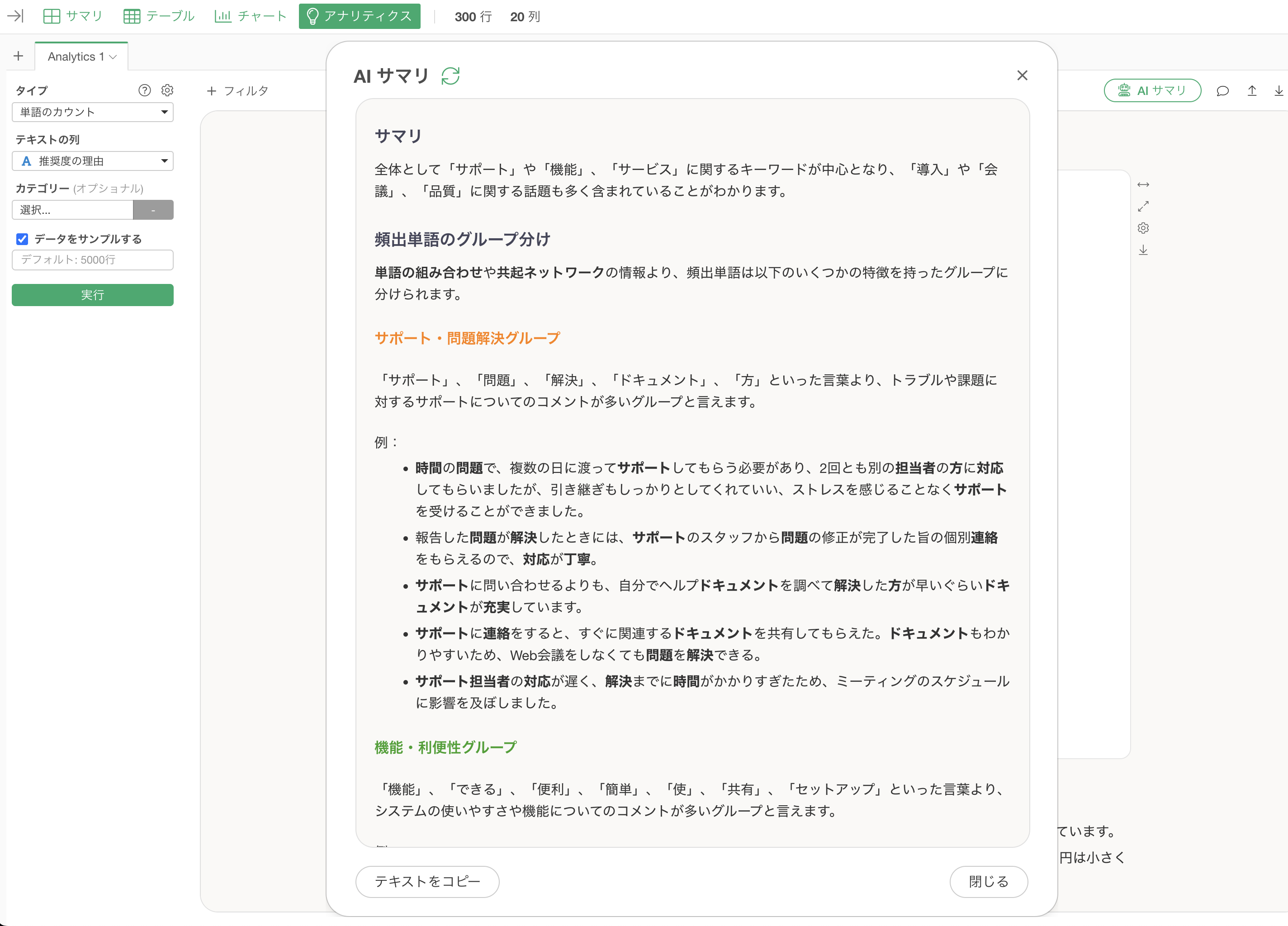
このAI サマリを見るだけでも、テキスト分析の結果としてどういった単語が多かったのか、どういうグループがあるのかをすぐに判断ができます。
さらには実際の文章の例も表示されるため、数値だけでは見えない顧客の声の背景まで理解できます。
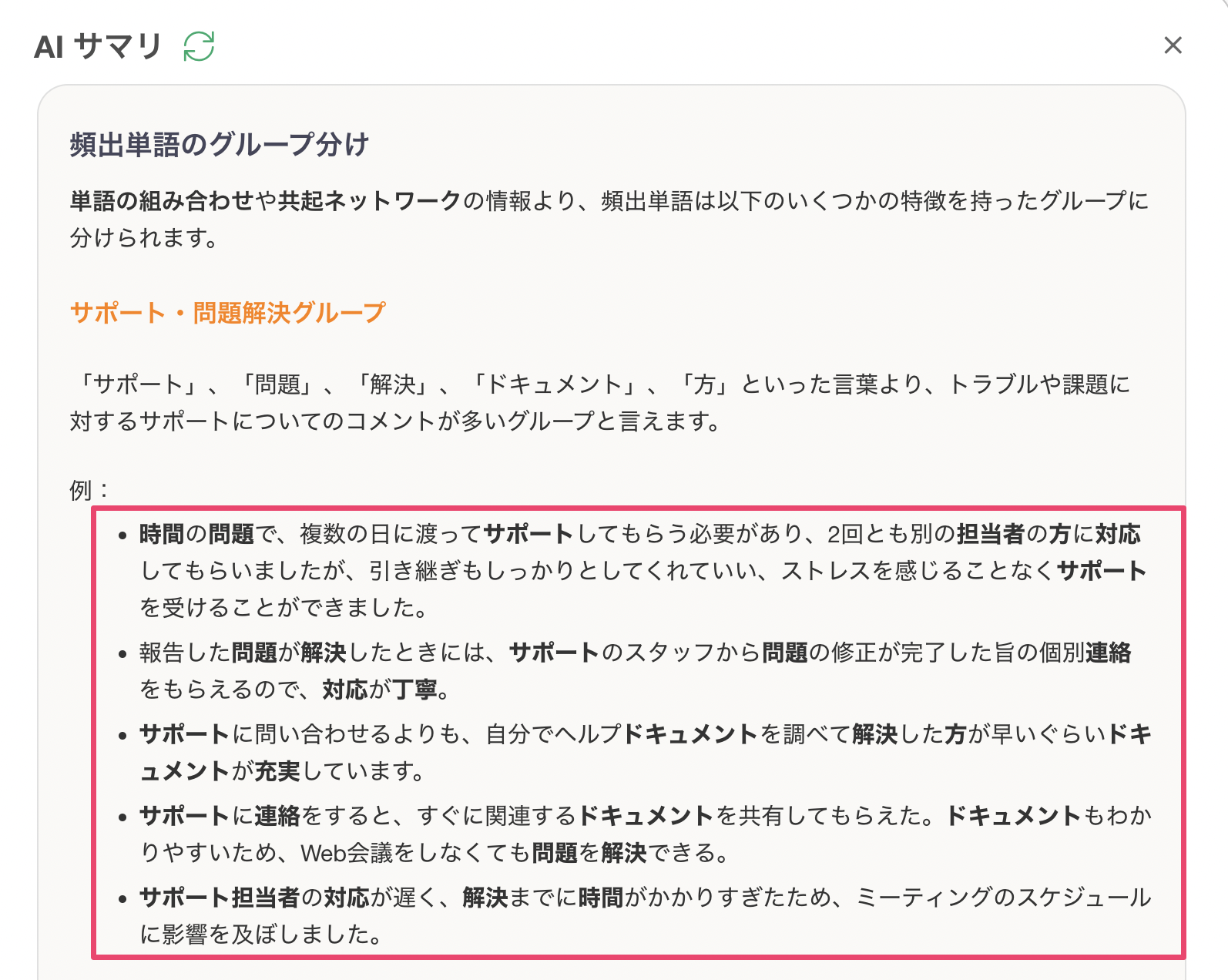
AI サマリ機能の詳細については、こちらのノートをご覧ください。
Exploratoryの使い方のアナリティクス編は以上となります！
Exploratoryの使い方シリーズ
Exploratoryの使い方シリーズの他のパートには下記のリンクからご確認いただけます。ぜひ次の「ダッシュボード」のパートも実施してみてください。